西安电子科技大学：《场论与复变函数》课程教学资源（课件讲义）第二章 解析函数 Analytic functions（主讲：付少忠）

第二章解析函数 历些毛子代拔大学 XIDIAN UNIVERSITY Analytic functions 第二章 解析函数 本章首先介绍复变函数的导数概念和求 导法则，在此基础上，介绍解析函数的概念 及判别法。 第一节 解析函数的概念 第二节 函数解析的充要条件 第三节 初等函数 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 2 第二章 解析函数 本章首先介绍复变函数的导数概念和求 导法则，在此基础上，介绍解析函数的概念 及判别法。 第一节 解析函数的概念 第二节 函数解析的充要条件 第三节 初等函数 第二章 解析函数 Analytic functions

第二章解析函数 历华毛子代枚士” XIDIAN UNIVERSITY Analytic functions 一、 复变函数的导数与微分 1、导数定义： 设w=f(z)定义于区域D,z∈D,zo+k∈D 如果i f(+4z)-f() 存在 △z→0 z 则称f(z)在z点可导，而极限值为f(z)在z点 的守数，r)成 7=Z 即r(a)=li f(3,+4z）-f(3】=i f(z)-f() 4z0 △z z→0 乙-Z0 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 3 一、复变函数的导数与微分 1、 导数定义: 第二章 解析函数 Analytic functions 设 定义于区域 , w f z D z D, z z D       0 0   0 0    z 0 f z z f z lim  z      如果 存在 则称 在 点可导，而极限值为 在 点 f z z f z z   0 0     0 0 z z dw f z dz  的导数，记作 或            0 0 0 0 0 0 0 z z z f z z f z f z f z f z lim lim  z z z            即

第二章解析函数 历安毛子代枝大学 XIDIAN UNIVERSITY Analytic functions 等价定义： Vε>0,38>0，当0<∠z<6时 恒有 园-ee 如果f(z)在区域D内处处可导，则称f(z)在D 内可导。导函数记为 f'(a)或 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 4 等价定义: 第二章 解析函数 Analytic functions           0 0 0 , , z 当 时       0 0 0 f z z f z f z z      恒有    如果 在区域 内处处可导， f z D   则称 f z D  在 内可导。导函数记为   dw f z dz  或

第二章解析函数 历些毛子代枝大学 XIDIAN UNIVERSITY Analytic functions 例1求f(z)=z的导数、 解：设z为复平面上任意一点 则 z+4z)2-z2 lim f(z+)-f(☒-im 4z→0 △z Λz0 △z =i(2z+4)=2z .f(z)=2z,即(z2)=2z 一般的， (z）=z(n为正整数) 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 5 第二章 解析函数 Analytic functions   2 例 求 的导数. 1 f z z  解: 设 为复平面上任意一点 z       2 2 z z 0 0 f z z f z z z z lim lim   z z           则      2 f z z, z z 2 2      即     n n 1 z nz n   一般的，  为正整数   0 2 2 z lim z z z      

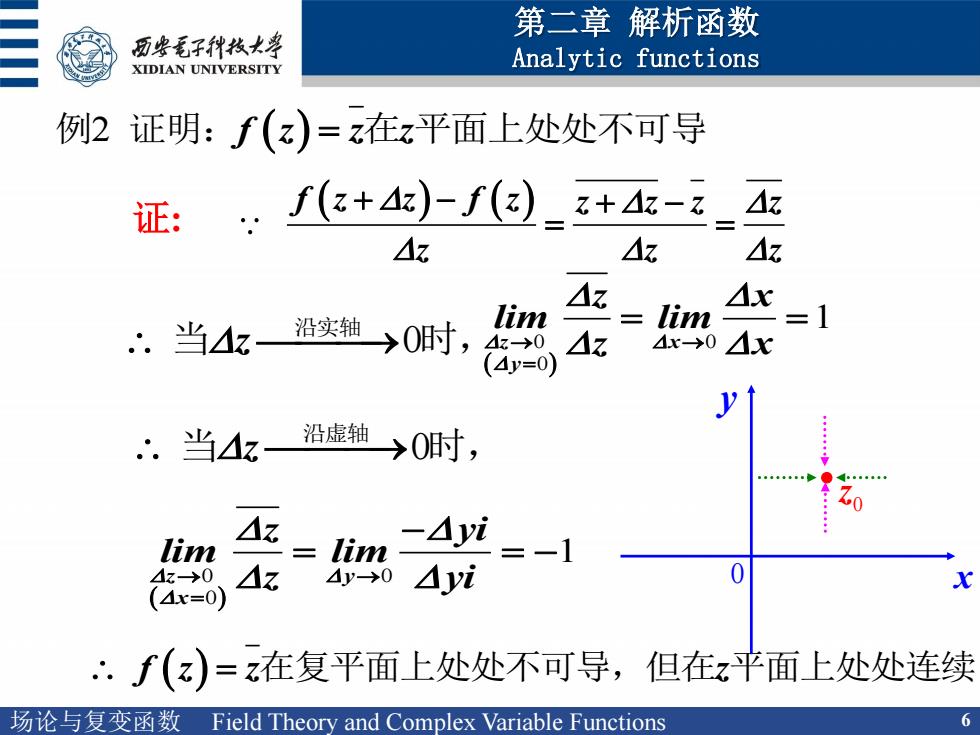
第二章解析函数 历安毛子代枝大学 XIDIAN UNIVERSITY Analytic functions 例2证明：f(z)=z在z平面上处处不可导 证：f(+4z)-f() △z z △z △z △x “.当沿实轴→0时， lim lim =1 4→0△z 4x0△X (4y=0) . 当4z— 沿虚轴 →0时， △z lim lim -△yi 4z→0、△z 40△yi 0 (4x=0) ∴.f(z)=z在复平面上处处不可导，但在z平面上处处连续 场论与复变函数Field Theory and Complex Variable Functions 6

场论与复变函数 Field Theory and Complex Variable Functions 6 第二章 解析函数 Analytic functions 例2 证明：f z z z    在 平面上处处不可导 证: f z z f z     z z z z z z z               z 0 当 沿实轴 时，  0 0 0 1 z x y z x lim lim   z x             z 0 当 沿虚轴 时，   0 0 0 1 z y x z yi lim lim   z yi               f z z z   在复平面上处处不可导，但在 平面上处处连续  0 z x y 0

第二章解析函数 历华毛子代枝大” XIDIAN UNIVERSITY Analytic functions 2.可导与连续的关系 f(z)在z点可导→f(z)在z点连续，反之，不成立。 证明：'(zo)存在，.ε>0,36>0，当0<4z<时 fa+4)-f3】-f(,)K8 z 记e(4)=,+)-/飞】-rk)则有rp(a)=0 .f(+k)-f()=f'()z+p(z)z 故f(名，+4)=f(2),即f(2)在z,点连续 反之：由例2可知f(z)=z处处连续，但处处不可导。 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 7 第二章 解析函数 Analytic functions 2. 可导与连续的关系     0 0 f z z f z z 在 点可导 在 点连续，反之，不成立。 证明: f z , , z  0 存在，           0 0 0 当 时       0 0 0 f z z f z f z z                 0 0 0 f z z f z z f z z       记      0 0 z lim z     则有        f z z f z f z z z z  0 0 0                   0 0 0 z 0 lim f z z f z , f z z    故   即 在 点连续 反之: 由例2可知 f z z    处处连续，但处处不可导

第二章解析函数 历些毛子种技大” XIDIAN UNIVERSITY Analytic functions 3.求导法则 (与高等数学相 同) () (c)'=0 c为复常数 (2)（z“）=z”,n为正整数 (3)[f(z)±g(z)]=f'(z)±g(z) (4)[f(z)g(z)]=f'(z)g(z)+f(z)g(z) 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 8 第二章 解析函数 Analytic functions 3. 求导法则 (与高等数学相 同) 1 0  c c    为复常数     1 2 n n z nz , n    为正整数 3 f z g z f z g z                   4 f z g z f z g z f z g z                      

第二章解析函数 历些毛子种枚大票 XIDIAN UNIVERSITY Analytic functions L得-a6r2ek 82(z) 2,g(z)≠0 (6){f[g(a2)]}=f"(w)g'(z),其中w=g(a) ()因-网 其中w=f(z)与z=p(w)是互为反函数的单值 函数，且p(w)≠0 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 9 第二章 解析函数 Analytic functions                   2 5 0 f z g z f z f z g z , g z g z g z             6  f g z f w g z , w g z                   其中       1 7 f z  w    其中w f z z w    与   是互为反函数的单值 函数，且w  0

第二章解析函数 历些毛子代枝大学 XIDIAN UNIVERSITY Analytic functions 4.微分的概念 设w=f(z)在z可导，则 Aw=f(zo+Az)-f(zo)=f(zo)4z+p(Az)Az 其中p(4)=0· P(Az)Az =0 △z 故p(4z)4z=o(4z) 称f'(z)△z为w=f(z)在z点的微分。 记作dw=f'(z) 场论与复变函数 Field Theory and Complex Variable Functions 10

场论与复变函数 Field Theory and Complex Variable Functions 10 第二章 解析函数 Analytic functions 4. 微分的概念   设w f z z  在 0 可导，则               w f z z f z f z z z z 0 0 0         0 0 z lim z     其中    0 0 z z z lim  z        故      z z o z     f z z w f z z  0 0   为 在 点的微分。   记作 dw f z dz    0  称

第二章解析函数 历些毛子种枚大票 XIDIAN UNIVERSITY Analytic functions 可见：可导分可微，且(z)= w dz z= 如果f(z)在区域D内每一点可微， 则称f(z)在D内可微 记作w=f'(z)k 场论与复变函数Field Theory and Complex Variable Functions 11

场论与复变函数 Field Theory and Complex Variable Functions 11 第二章 解析函数 Analytic functions   0 0 z z dw f z dz  可见：可导 可微，且    如果 在区域 内每一点可微， f z D   则称 在 内可微. f z D   记作 dw f z dz   