《线性代数Ⅱ》课程教学大纲 课程基本信息(Course Information) 课程代码 学纷 Hours) *课程名称 (中文)线性代数Ⅱ (Course Name】 (英文)Linear albraⅡ 课程类型 双学位基础必修课 授课对象 (Target 双学位学生 Audience) 授课语言 (Language of 双语 Instruction) 开课院系 (School) 数学科学学院 先修课程 后续课程 无 (Prerequisite) 傲学类专业课程 (nost) *课程负责人 课程网址 李古有 (Course (Instructor) Webpage) 本课程是为修读面上《线性代数》的双学士学位学生开设的后续课程,其难 度略高于数学系《高等代数》的要求, 略低于数学系《高等代数》的要 。 高等代数是数 专业本科教学的最重要的基础课程之一,其基本内容为 多项式、线性方程组、线性空间、线性映射、线性算子谱理论、多重线性代 课程简介(中 数、若当标准型理论等等,具有高度的抽象性与广泛的应用性,是人类思维 文) 高度发展的象征。高等代数是代数学的重要内容。我国古代数学发展的主线 都与代数学,尤其是高等代数学密切相关,以中国剩余定理为光辉代表。当 代信息社会中,计算机、网络、通信、信息安全 视频图像处理中很多基而 理论源于高等代数。本课程的目标是使学生通过课程的学习,对线性代数 生根本的兴趣,为进一步学习高等代数抽象理论建立良好基础。 (苹文300.500字) 课程简介(英 inear algebra is one of the fundamental courses in physics.It also plays an 文) important role in physics,engineering and computer sciences.Its main (Description) contents include linear equations,linear space,linear mapping,linear operato spectrum theory,multilinear algebra,Jordan standard theory,polynomial,etc
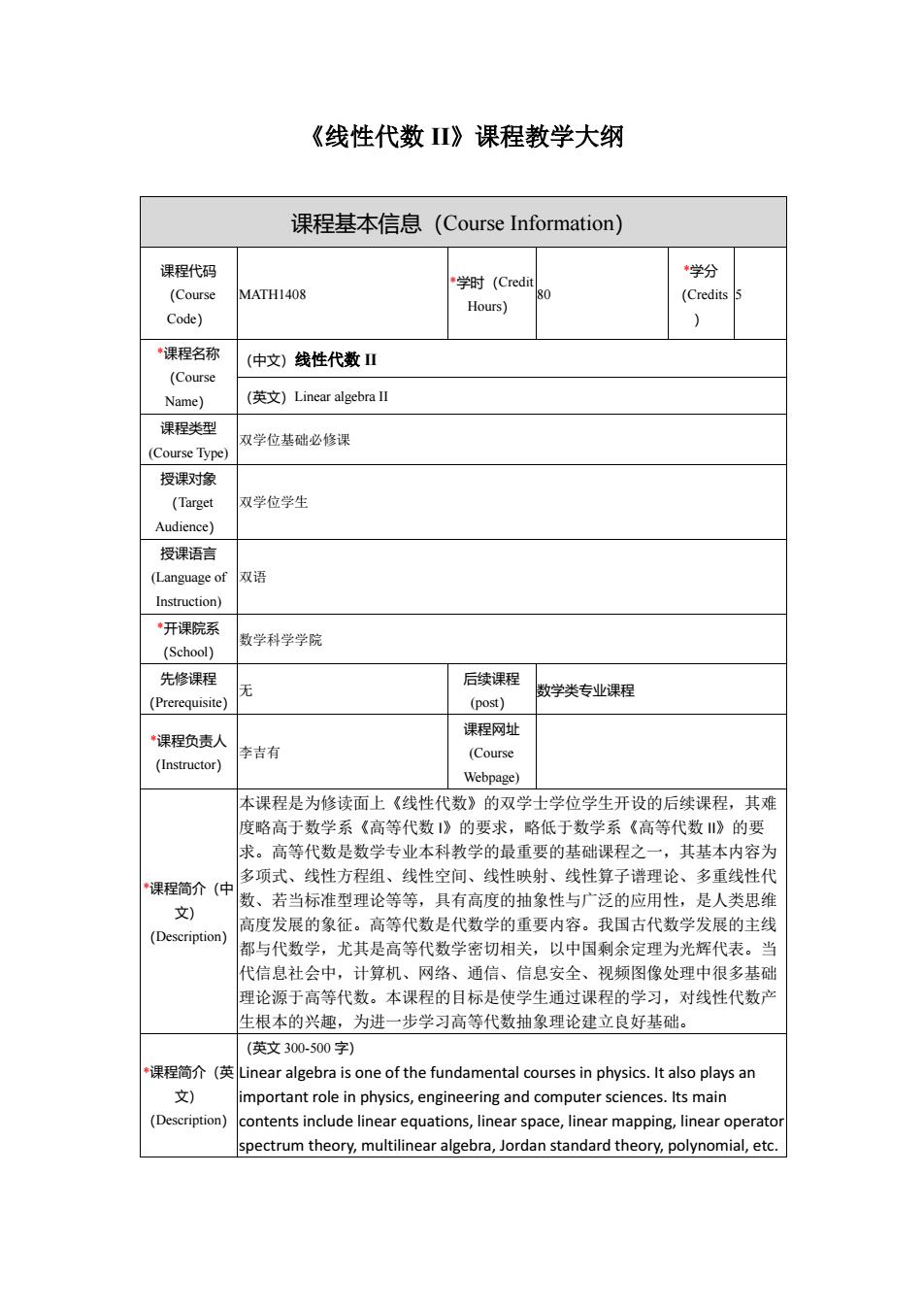
《线性代数 II》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH1408 *学时(Credit Hours) 80 *学分 (Credits ) 5 *课程名称 (Course Name) (中文)线性代数 II (英文)Linear algebra II 课程类型 (Course Type) 双学位基础必修课 授课对象 (Target Audience) 双学位学生 授课语言 (Language of Instruction) 双语 *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 无 后续课程 (post) 数学类专业课程 *课程负责人 (Instructor) 李吉有 课程网址 (Course Webpage) *课程简介(中 文) (Description) 本课程是为修读面上《线性代数》的双学士学位学生开设的后续课程,其难 度略高于数学系《高等代数 I》的要求,略低于数学系《高等代数 II》的要 求。高等代数是数学专业本科教学的最重要的基础课程之一,其基本内容为 多项式、线性方程组、线性空间、线性映射、线性算子谱理论、多重线性代 数、若当标准型理论等等,具有高度的抽象性与广泛的应用性,是人类思维 高度发展的象征。高等代数是代数学的重要内容。我国古代数学发展的主线 都与代数学,尤其是高等代数学密切相关,以中国剩余定理为光辉代表。当 代信息社会中,计算机、网络、通信、信息安全、视频图像处理中很多基础 理论源于高等代数。本课程的目标是使学生通过课程的学习,对线性代数产 生根本的兴趣,为进一步学习高等代数抽象理论建立良好基础。 *课程简介(英 文) (Description) (英文 300-500 字) Linear algebra is one of the fundamental courses in physics. It also plays an important role in physics, engineering and computer sciences. Its main contents include linear equations, linear space, linear mapping, linear operator spectrum theory, multilinear algebra, Jordan standard theory, polynomial, etc
The main goal of this course is to enable students to have a solid base of understanding in linear algebra.Geometric viewpoints will be emphasized throughout the course. 课程目标与内容(Course objectives and contents) 能理解线性代数的基本理论,提高抽象思维能力。(B1) *课程目标 2.能运用线性代数的基本方法,解决一些基本的线性问题。(B2) (Course Objeet)能引导学生培养自我学习能力,并养成终身学习的习惯。(C5) 4.引导学生形成批判性思维,并将高等代数运用于实践,加以创新,解决新的问题。(C3) 课程目标 毕业要求指标点 毕业要求指标 卫.比较实的数学基础.比蚊强的罗组及 点与课程目标 速程目标2 的对应关系 课程目标4 形象思维能力,对问题的总体把振和归 (根据学院要 纳能力 求填写) 勤于思考,善于钻研,对于推骑出新怀 有浓厚的兴趣。富有探素情神并渴望解 课程目标3 问题 学内容(要点)学目标 学时 散学形作业及考核棵程思政对应 要求 融入点程目标 第 理论课 课程导 直观理轻 与习圆教材习题系统思维A4 周 “教学内容进第 饯性空间、子空子空间计算 厘论课 认识论和 度安及对 应课程目标周 间、四个子空间、与直和分解 与习题做材习题 方法论 (Class 第一 四个子空间、直和 理解线性 理论课 材习题 Schedule & 分解,线性代数 创新思维 Requirements周 数本定理 与习题 本定理 Course第 Objectives) 四 内积空间 内积空间 与习题胶材习颗 理论课 创新思维B 投影与正交化 哩论课 五方法及其应用 理解和掌据 学科知识B1 最小二乘法 与习题教材习题 周第 理论课 行列式重探 计算行列式 与习题散材习题 认识论和 4.BI 周 课 方法论
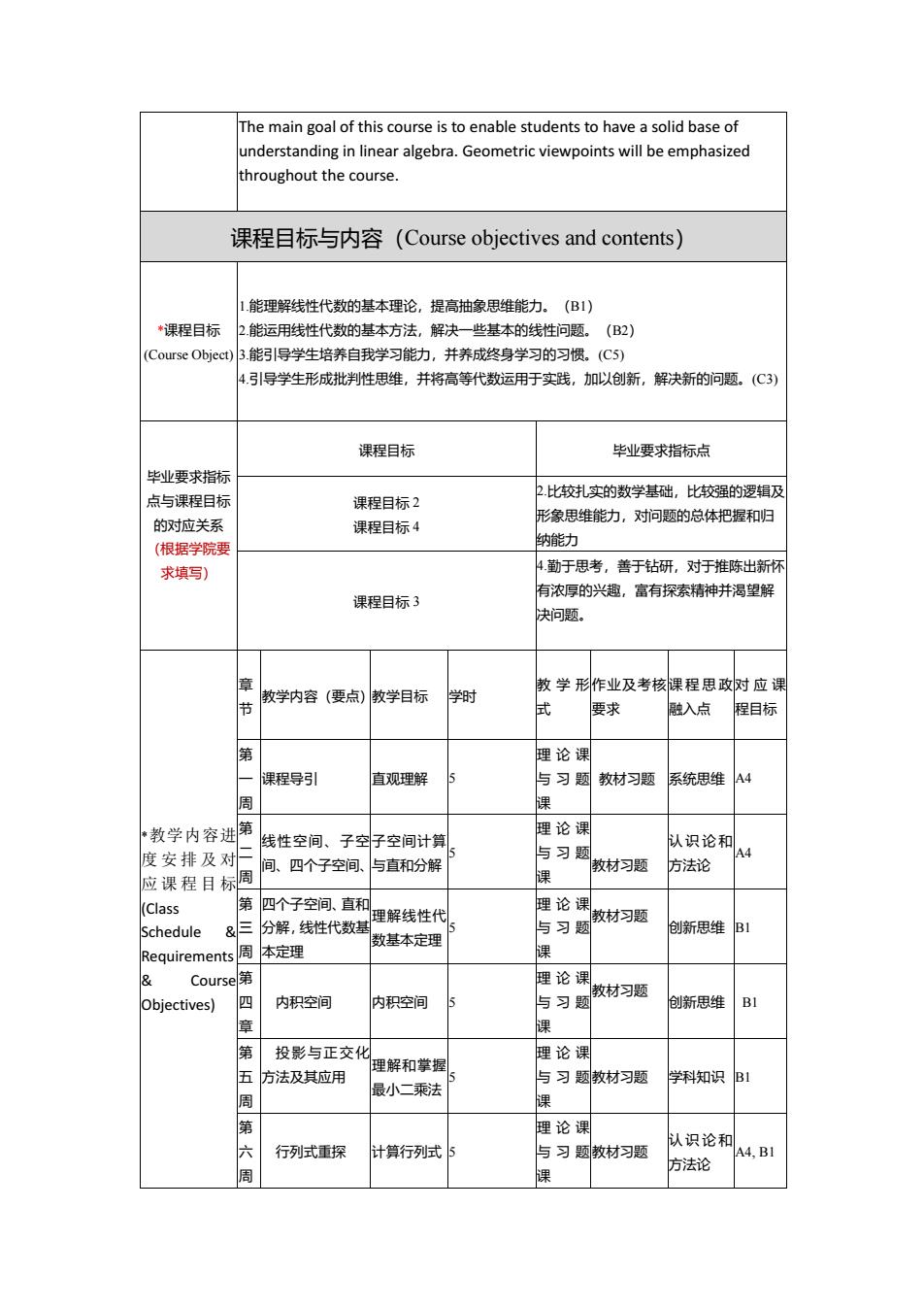
The main goal of this course is to enable students to have a solid base of understanding in linear algebra. Geometric viewpoints will be emphasized throughout the course. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 1.能理解线性代数的基本理论,提高抽象思维能力。(B1) 2.能运用线性代数的基本方法,解决一些基本的线性问题。(B2) 3.能引导学生培养自我学习能力,并养成终身学习的习惯。(C5) 4.引导学生形成批判性思维,并将高等代数运用于实践,加以创新,解决新的问题。(C3) 毕业要求指标 点与课程目标 的对应关系 (根据学院要 求填写) 课程目标 毕业要求指标点 课程目标 2 课程目标 4 2.比较扎实的数学基础,比较强的逻辑及 形象思维能力,对问题的总体把握和归 纳能力 课程目标 3 4.勤于思考,善于钻研,对于推陈出新怀 有浓厚的兴趣,富有探索精神并渴望解 决问题。 *教学内容进 度安排及对 应课程目标 (Class Schedule & Requirements & Course Objectives) 章 节 教学内容(要点)教学目标 学时 教学形 式 作业及考核 要求 课程思政 融入点 对应课 程目标 第 一 周 课程导引 直观理解 5 理论课 与习题 课 教材习题 系统思维 A4 第 二 周 线性空间、子空 间、四个子空间、 子空间计算 与直和分解 5 理论课 与习题 课 教材习题 认识论和 方法论 A4 第 三 周 四个子空间、直和 分解,线性代数基 本定理 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 创新思维 B1 第 四 章 内积空间 内积空间 5 理论课 与习题 课 教材习题 创新思维 B1 第 五 周 投影与正交化 方法及其应用 理解和掌握 最小二乘法 5 理论课 与习题 课 教材习题 学科知识 B1 第 六 周 行列式重探 计算行列式 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1
诺理论、对 特征值与特征向角化主对 理论课 t 量,对角化, 二一次称矩阵 与习题牧材习题 学科知识 A4,BI 型,Jordan标准型次型、Jordar 标准型 谱理论、 特征值与待征向角化 实对 理论课 八屋,对角化,二次称炬阵 与习题教材习题 学科知识A4,B1 周里,Jordan标准型次型、Jordan 标推型 热理论 ,对 特征值与特征向角化、实 理论课 ☆慢 与习题教材习题 学科知识A4,B 课 标准型 理论课 4 SVD分解及其应理解sVD及 解决实际B1 用 其简单应用 与习题散材习题 问题 第 饯性映射初步、线理解线性代 理论课 认识论和 与习题教材习题 4,BI 性代数基本定理数基本定理 防法论 生缺射初步 理解线性什 理论课 认识论和 百习题敦材习题 A4.B 性代数基本定理 数基本定理 方法论 周 第 多项式与群环域 理论课 正确认ALA3 与习题教材习题 中国古行 BI B3 数本定理 歇成就 周 性算子的 里解线性 理论课 认识论 论、商空间 与习题敢材习题 方法论 A4,BI 理论课闺 积间上的筒理解线性代 子理论. 诺定理数基本定理 与习材习题 认识论和 A4 R 方法论 十复数域上的若当掌握若当标 理论阑 认识论和 与习顾教材习题 A4 BI 标准型理论 型理论 课 方法论 周
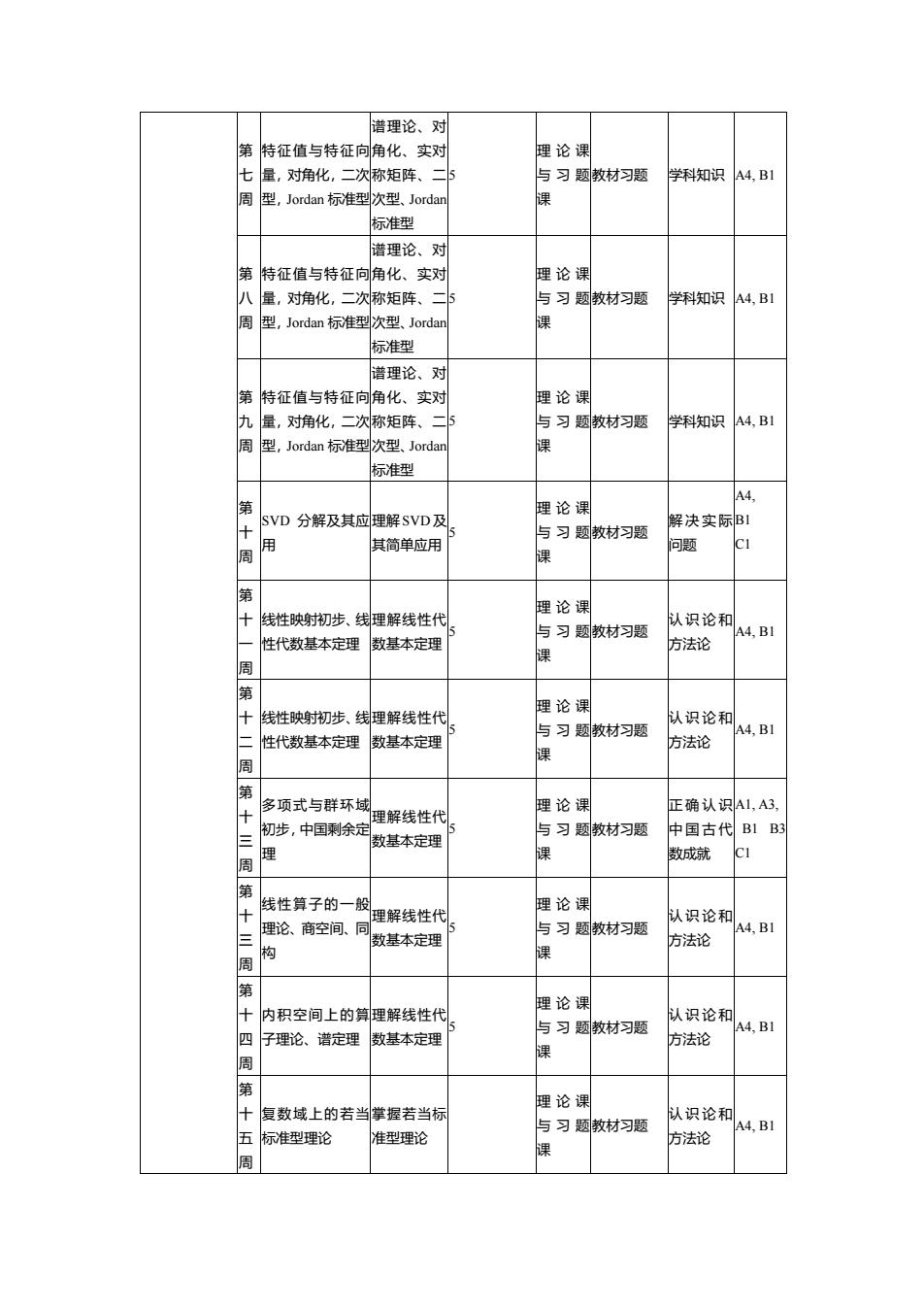
第 七 周 特征值与特征向 量,对角化,二次 型,Jordan 标准型 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型 5 理论课 与习题 课 教材习题 学科知识 A4, B1 第 八 周 特征值与特征向 量,对角化,二次 型,Jordan 标准型 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型 5 理论课 与习题 课 教材习题 学科知识 A4, B1 第 九 周 特征值与特征向 量,对角化,二次 型,Jordan 标准型 谱理论、对 角化、实对 称矩阵、二 次型、Jordan 标准型 5 理论课 与习题 课 教材习题 学科知识 A4, B1 第 十 周 SVD 分解及其应 用 理解 SVD 及 其简单应用 5 理论课 与习题 课 教材习题 解决实际 问题 A4, B1 C1 第 十 一 周 线性映射初步、线 性代数基本定理 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1 第 十 二 周 线性映射初步、线 性代数基本定理 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1 第 十 三 周 多项式与群环域 初步,中国剩余定 理 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 正确认识 中国古代 数成就 A1, A3, B1 B3 C1 第 十 三 周 线性算子的一般 理论、商空间、同 构 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1 第 十 四 周 内积空间上的算 子理论、谱定理 理解线性代 数基本定理 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1 第 十 五 周 复数域上的若当 标准型理论 掌握若当标 准型理论 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1

第 性代数应用进 了解初步 理论课 认识论和 与习题材习题 A4.B 访法论 周 注1:津议按照教学周周学时编排,以使白动生成教学日历 注2: 相应章节的课程思政融入点根据实际请况填写。 课程目标 理程而 平时作业(30 期未考试课程目标 课程目 日(0 杜制 考核方式 分) 分) (70分) 权重 课程目标1 b.35 课程目达成 度评价 课程目标2 b.3 〔根据学院要 求填马) 课程目标3 o.15 课程目标4 10 *考核方式 示例 (1)平时成绩30分 (Grading) (3)期末考试70分 (必含信总:教材名称,作者, 出版社,出版年份,版次,书号) L.Linear algebra done right,,S.xler,Springer,2015,第二版ISBN 9780387982588.(中译版:线性代数应该这样学,人民邮电出版社,2016) Introduction to Linear Algebra, G.Strang,Wellesley-Cambridg Press,2016,第五版.15BWN:978-09802327-7-6. 教材或参考资3。《高等代数》,北京大学数学系几何与代数教研室编,高等教有出版社, 料(Textbooks2003. &Other Materials) 线性代数五讲》,龚升著,科学出版社,2005 5. 《高等代数》,丘维声著,北京大学出版社,2006. 6. 《高等代数学》,张贤科著,清华大学出版社,1997 柯斯特利金, 《代数学引论L,I山,I1I》,张英伯等译,高等教有出 社,2006
第 十 六 周 线性代数应用选 讲 了解初步应 用 5 理论课 与习题 课 教材习题 认识论和 方法论 A4, B1 注 1:建议按照教学周周学时编排,以便自动生成教学日历。 注 2:相应章节的课程思政融入点根据实际情况填写。 课程目标达成 度评价 (根据学院要 求填写) 课程目标 考核方式 平时作业(30 分) 课程项 目 (0 分) 期末考试 (70 分) 课程目标 权重 课程目 标达成 度 课程目标 1 10 10 30 0.35 课程目标 2 10 10 20 0.3 课程目标 3 0 5 10 0.15 课程目标 4 10 5 10 0.2 *考核方式 (Grading) 示例: (1)平时成绩 30 分 (3)期末考试 70 分 *教材或参考资 料 (Textbooks & Other Materials) (必含信息:教材名称,作者,出版社,出版年份,版次,书号) 1. Linear algebra done right,S. Axler, Springer, 2015,第二版 ISBN 9780387982588.(中译版:线性代数应该这样学,人民邮电出版社,2016) 2. Introduction to Linear Algebra, G. Strang, Wellesley-Cambridge Press,2016, 第五版. ISBN: 978-09802327-7-6. 3.《高等代数》,北京大学数学系几何与代数教研室编,高等教育出版社, 2003. 4. 《线性代数五讲》,龚升 著, 科学出版社,2005. 5. 《高等代数》,丘维声 著,北京大学出版社,2006. 6. 《高等代数学》,张贤科 著,清华大学出版社,1997. 7. 柯斯特利金,《代数学引论 I,II,III》,张英伯等译,高等教育出版 社,2006

8.矩阵理论与应用,张跃辉,科学出版社,2011,第一版. 其它(More) 备注(Notes)) 备注说明: 1.带*内容为必填项。 2.课程简介字数为300-500字:课程大纲以表述清楚教学安排为宜,字数不限
8. 矩阵理论与应用,张跃辉,科学出版社,2011,第一版. 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限