西安电子科技大学：《场论与复变函数》课程教学资源（课件讲义）第三章 复变函数的积分 Integrals of complex variable functions

第三章复变函数的积分 历些毛子种技大学 XIDIAN UNIVERSITY Integrals of complex variable functions 第一节 复变函数积分的概念 第二节 柯西-古萨基本定理(Cauchy-Goursat 第三节 基本定理(C-G)的推广一复合闭路定理 第四节原函数与不定积分 第五节 柯西积分公式 第六节 解析函数的高阶导数公式 第七节1 解析函数与调和函数的关系 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 2 2 第三章 复变函数的积分 Integrals of complex variable functions 第一节 复变函数积分的概念 第二节 柯西-古萨基本定理(Cauchy-Goursat 第三节 基本定理(C-G)的推广—复合闭路定理 第四节 原函数与不定积分 第五节 柯西积分公式 第六节 解析函数的高阶导数公式 第七节 解析函数与调和函数的关系

历安毛子代枚大学 XIDIAN UNIVERSITY 1积分的定义 复变函数积分 第一节 ○2.积分存在的条件及其计算法 ○3.积分的性质 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 3 1.积分的定义 2.积分存在的条件及其计算法 3.积分的性质 第 一 节 复 变 函 数 积 分

历安毛子代枚大学 1.积分的定义 XIDIAN UNIVERSITY 有向曲线： 设C为平面上给定的一条光滑（或按段光滑） 曲线，如果选定C的两个可能方向中的一个作 为正方向（或正向），那么称C为有向曲线.(C) C:z(t)=x(t)+iy(t),t∈[，B] B z'(t)=x'(t)+y'(t)≠0，t∈[x,B] z)是一一的 场论与复变函数 Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 4 1. 积分的定义 有向曲线: 设C为平面上给定的一条光滑(或按段光滑) 曲线, 如果选定C的两个可能方向中的一个作 为正方向(或正向), 那么称C为有向曲线. x y o A B ( ) C  C： z(t)是一一的

历安毛子代枚大学 1.积分的定义 XIDIAN UNIVERSITY 1.定义设w=f(z)在区域D内有定义，C为D内 一条光滑的有向曲线（如图） (1)分割：分割AB为zk-乙k(k=1…n) (2)作和：5.∈k-1 S。=∑f(5)z4-z） 216成， 其中△k=乙k一乙k-1 记△S为zk-1Zk的长度，6=x{ASk} 1≤k≤n 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 5 设 在区域 内有定义， 为 内 w f z D C D    1分割： 分割 为   AB z z k n k 1 k   1  2 k k k 1  z z 作和：   1. 定义 D A B   k 1 z  k z k s 一条光滑的有向曲线（如图）   1  1 n n k k k k S f z z         1 n k k k f z      k k k 1 z z z 其中    1   1 k k k k k n S z z max S     记 为 的长度，    c 1. 积分的定义

历些毛子种枚大兽 1.积分的定义 XIDIAN UNIVERSITY (3)取极限：1im∑f(G)△zs 8→>0k=1 11->co 若极限存在，则极限值称为=f(z)沿C的积分， 记作 J.()d(. 注：1若C封闭，记为f(z)k,其中C表示正向， 反向为C. 2° 当C是x轴上的线段，a≤x≤b,且f(z)=u(x) 则cf(z)k=∫u(x) 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 6   0 1 3 ( ) n k k n lim f z     取极限：    若极限存在，  0 1 ( ) n k c k f z dz lim f z   记作       则极限值称为 沿 的积分， w f z C    注：   C C f z dz C  1 若 封闭，记为 ,其中 表示正向， 2 当 是 轴上的线段， ,且 , C x a x b f z u x            b C a f z dz u x dx  则  C 反向为 . 1. 积分的定义

历柴毛子代枚大学 2.积分的性质 XIDIAN UNIVERSITY 复积分与实变函数的定积分有类似的性质. 1∫c[kf(a)+kg(z]-k∫cf(a)k+kcg(a) 2∫cf(z)k=-∫cf(z)k 3设C=C+C2+…+Cm, Sf(z)d=Sf(z)+Sf(z)++Sf(z)d 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 7 1 2 1 2         C C C   k f z k g z dz k f z dz k g z dz         1 2     C C f z dz f z dz      3 C C C C ,     1 2 n 设         C C C C 1 2 n f z dz f z dz f z dz f z dz     则    复积分与实变函数的定积分有类似的性质. 2. 积分的性质

历安毛子代枝大学 2.积分的性质 XIDIAN UNIVERSITY (4)f()dsf(d=()dssML, 其中，M=max|f(z川， 第一类曲线积分 L为曲线C的弧长。 证明 ()(s(c.). . 取极限得：cf(a)≤∫c(zs≤M=ML 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 8 证明       1 1 1 n n n k k k k k k k k k f z f z f s                   C C C f z dz f z ds M ds ML    取极限得：    第一类曲线积分    C C (4) | f (z)dz| | f (z)||dz|   C | f (z)|ds 其中， M max | f (z)|, zC  L为曲线C的弧长。  ML , 2. 积分的性质

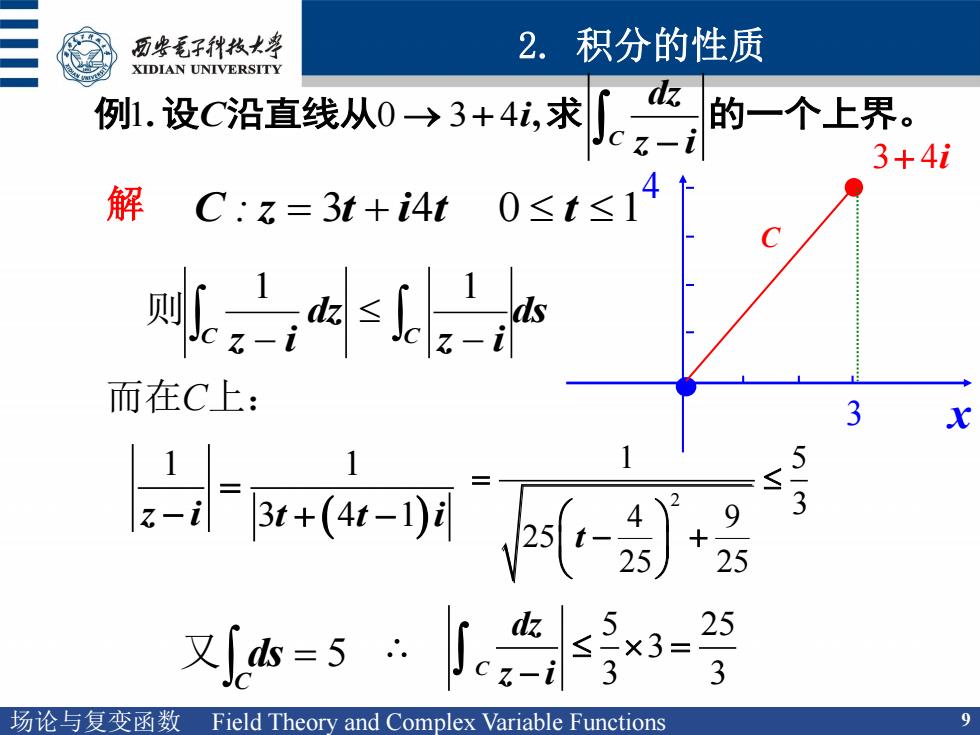
历要毛子代枝大” 2.积分的性质 XIDIAN UNIVERSITY 刚设c沿直线0→3+4求 的一个上界。 3+4i 解 C:=3t+i4t 0≤t≤14 zs'热 而在C上： 间- 5 3 又=5小x=胃 3 场论与复变函数Field Theory and Complex Variable Functions

场论与复变函数 Field Theory and Complex Variable Functions 9 1 0 3 4 . , C dz C i z i    例 设 沿直线从 求  的一个上界。 解 C : z  3t  i4t 0  t 1 ds z i dz z i C C    1 1 则 而在C上：   1 1 z i 3 4 1 t t i     x  3 4  3 4  i C 2 1 5 3 4 9 25 25 25 t            5 C 又 ds 5 25 3 C 3 3 dz z i       2. 积分的性质

历安毛子代枚大等 3.积分存在的条件极其计算 XIDIAN UNIVERSITY 定理1.积分存在性定理： 如果f(z)=u(x,y)+iv(x,y)在按段光滑曲线 C上连续，则积分∫f(2)d一定存在。 证： 设光滑曲线C由参数方程给出 z=z(t)=x(t)+iy(t),≤t≤B 并且z'(t)≠0，t∈(C,B), 设5k=5k+i训k, 场论与复变函数Field Theory and Complex Variable Functions 10

场论与复变函数 Field Theory and Complex Variable Functions 10 证: ( ) ( ) ( ), C z z t x t i y t t        设光滑曲线 由参数方程给出 ( ) ( , ) ( , ) , ( )d C f z u x y iv x y C f z z    如果 在按段光滑曲线 上连续 则积分 一定存在。 定理1. 积分存在性定理： 并且 ( ) 0, ( , ), z t t      , k k k 设     i 3. 积分存在的条件极其计算

历安毛子代枚大学 XIDIAN UNIVERSITY 因为△Zk=乙k-Zk-1=Xx+yk-(化k-+yk-1) =△比k+iyk, 所以∑f5x)AzE k=1 =2u(5,x)+iv5,7:l△+) =2Iu(5,x)Ax&-5,n:)Al +i∑Iy(5,1k)△x+u(5k,nk)Ay] 场论与复变函数Field Theory and Complex Variable Functions 11

场论与复变函数 Field Theory and Complex Variable Functions 11 ( )  k  k  k1  k  k  k1  k1 因为 z z z x iy x iy , k k  x  iy k n k k  f z 1 所以 ( )       n k k k k k k k u i v x i y 1 [ ( , ) ( , )]( )             n k k k k k k k n k k k k k k k i v x u y u x v y 1 1 [ ( , ) ( , ) ] [ ( , ) ( , ) ]        