《最优化方法》课程教学大纲 课程基本信息(Course Information) 课程代码 学时 MATH3806 学纷 (Course (Credits) Hours) 课程名称 (中文)最优化方法 (Course Name) (英文)Optimization Methods 课程类型 (Course Type) 专业方向选修课 授课对家 (Target 本科生 Audience) 授课语言 (Language of 全中文(英文讲义) Instruction) “开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 数学分析,高等代数 后续课程 (nost) “课程负责人 课程网址 (Course (Instructor) Webpage) 本课程主要介绍优化理论和典型的优化算法(包括线性规划的单纯形法,对偶 理论 凸优化简介及内点法), 课堂以理论讲授为主,课下需要学生学习程 课程简介(中 编写及分析计算结果。 具体主题包括 线性规划理论,单纯形法及其分析 ) 2. (Description) 凸集、凸函数及凸优化基本概念,梯度下降及牛颜法在强凸函数 下的收敛性分析 对偶理论,KKT条件介绍 凸优化的内点法 This course is to give an introduction to the basic theories and algorithms in optimization,including the simplex method in linear programming,the convex optimization,dual theory and the interior point method.Currently,the tentativ pics in thiscour are as follows (Descripion) Theories of linear programming;the simplex method. 2.Introduction to convex optimization,the convergence of gradient descent and Newton's method for strongly convex functions
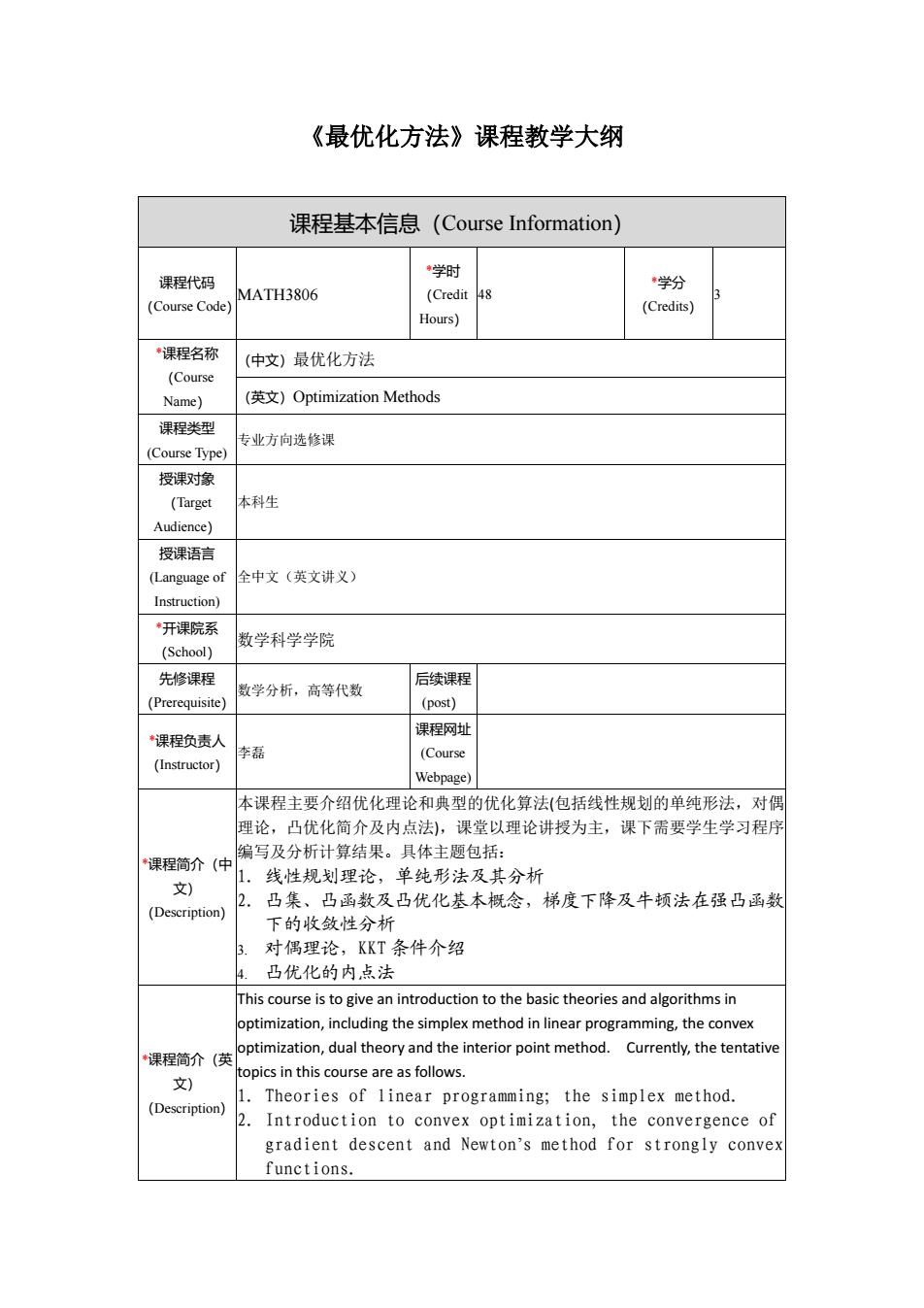
《最优化方法》课程教学大纲 课程基本信息(Course Information) 课程代码 (Course Code) MATH3806 *学时 (Credit Hours) 48 *学分 (Credits) 3 *课程名称 (Course Name) (中文)最优化方法 (英文)Optimization Methods 课程类型 (Course Type) 专业方向选修课 授课对象 (Target Audience) 本科生 授课语言 (Language of Instruction) 全中文(英文讲义) *开课院系 (School) 数学科学学院 先修课程 (Prerequisite) 数学分析,高等代数 后续课程 (post) *课程负责人 (Instructor) 李磊 课程网址 (Course Webpage) *课程简介(中 文) (Description) 本课程主要介绍优化理论和典型的优化算法(包括线性规划的单纯形法,对偶 理论,凸优化简介及内点法),课堂以理论讲授为主,课下需要学生学习程序 编写及分析计算结果。具体主题包括: 1. 线性规划理论,单纯形法及其分析 2. 凸集、凸函数及凸优化基本概念,梯度下降及牛顿法在强凸函数 下的收敛性分析 3. 对偶理论,KKT 条件介绍 4. 凸优化的内点法 *课程简介(英 文) (Description) This course is to give an introduction to the basic theories and algorithms in optimization, including the simplex method in linear programming, the convex optimization, dual theory and the interior point method. Currently, the tentative topics in this course are as follows. 1. Theories of linear programming; the simplex method. 2. Introduction to convex optimization, the convergence of gradient descent and Newton’s method for strongly convex functions
Dual theory and KKT conditions Theinterior ethod for convex 课程目标与内容(Course objectives and contents) 该课程重点培养学生利用数学知识分析问恩、设计算法的能力,为后续研究打 下相应基础。 *课程目标 1.掌据最优化的基木概念,数学理论(线性规划,凸优化,对偶的概念性质) 理解最优化算法的设计思路,提高专业基础。 (B1B2.C1) ourse bje 2.掌握典型的最优化算法 (单纯形法,梯度下降,牛顿法,内点法等),掌 算法分析技巧,了解前沿研究课题。(B2,B4,C1,C5) 3.训练程序设计的能力,将设计的算法实现出来,解决实际问题。(A4,C5,D1 教学纳 章节容(要教学目标 动 教学形式 作业及考课程思政融入 对应课程目 核要求 点 标 点) 示例: 理2性灯 2次作业 线性规别其理 挤养学生立 第 划理论 掌握熱悉 及顶 的A 面授 思考能力和条 1,2,3 部分单纯形用。草握单 基本 理清的思生 形法,能够程 能第程序 方式 序实现 实现算法 敦学内容进度 理解凸集凸 3次作业, 安排及对应课 含编程题 程目标(Clas 解相关基本 目。能够理培养学生认 Schedule& 性质.了解凸 论证明一严谨的工作作 Requirements&第二凸优化优化的典型 些简单性风。独立思考 Course 部分理论 问题,掌握梯 面授 1,2,3 Objectives) 度下降和 倾法在强凸 法,用以解维方式 情形的收敛 决一些实刻 性证明. 际问题, 1次作业 时偶理理解对偶儒 能够熟到 第三论及念掌握相关 导出问划 培养学生逻铝 性质,理解与 面授 的对烟治 1 部分KKT条熟知KKT条 明维能力 顾,熟练写 第四内点法理解与掌 9 面授 1次作业。培养学生独立1,2,3
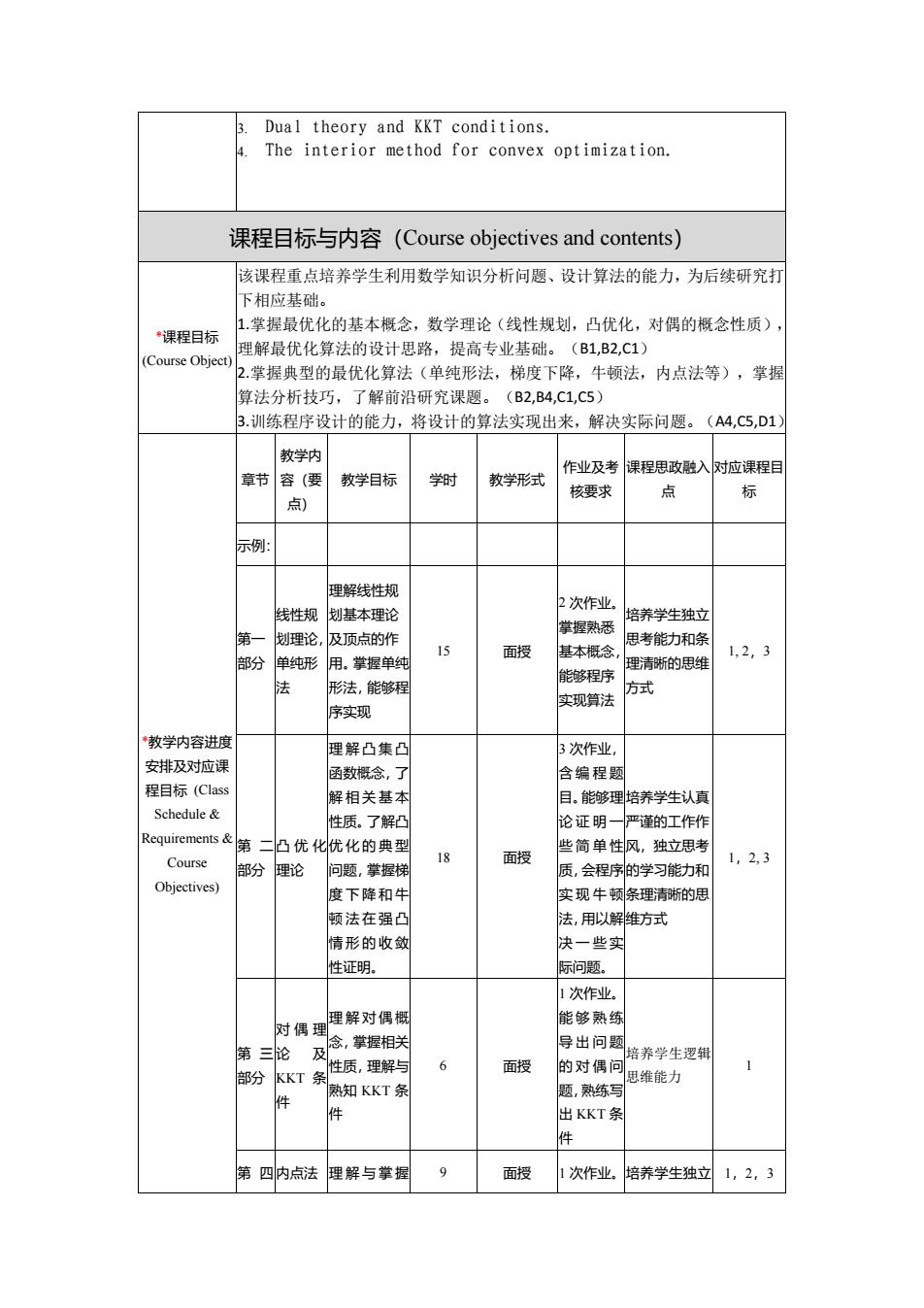
3. Dual theory and KKT conditions. 4. The interior method for convex optimization. 课程目标与内容(Course objectives and contents) *课程目标 (Course Object) 该课程重点培养学生利用数学知识分析问题、设计算法的能力,为后续研究打 下相应基础。 1.掌握最优化的基本概念,数学理论(线性规划,凸优化,对偶的概念性质), 理解最优化算法的设计思路,提高专业基础。(B1,B2,C1) 2.掌握典型的最优化算法(单纯形法,梯度下降,牛顿法,内点法等),掌握 算法分析技巧,了解前沿研究课题。(B2,B4,C1,C5) 3.训练程序设计的能力,将设计的算法实现出来,解决实际问题。(A4,C5,D1) *教学内容进度 安排及对应课 程目标 (Class Schedule & Requirements & Course Objectives) 章节 教学内 容(要 点) 教学目标 学时 教学形式 作业及考 核要求 课程思政融入 点 对应课程目 标 示例: 第一 部分 线性规 划理论, 单纯形 法 理解线性规 划基本理论 及顶点的作 用。掌握单纯 形法,能够程 序实现 15 面授 2 次作业。 掌握熟悉 基本概念, 能够程序 实现算法 培养学生独立 思考能力和条 理清晰的思维 方式 1, 2,3 第 二 部分 凸优化 理论 理解凸集凸 函数概念,了 解相关基本 性质。了解凸 优化的典型 问题,掌握梯 度下降和牛 顿法在强凸 情形的收敛 性证明。 18 面授 3 次作业, 含编程题 目。能够理 论证明一 些简单性 质,会程序 实现牛顿 法,用以解 决一些实 际问题。 培养学生认真 严谨的工作作 风,独立思考 的学习能力和 条理清晰的思 维方式 1,2, 3 第 三 部分 对偶理 论 及 KKT 条 件 理解对偶概 念,掌握相关 性质,理解与 熟知 KKT 条 件 6 面授 1 次作业。 能够熟练 导出问题 的对偶问 题,熟练写 出 KKT 条 件 培养学生逻辑 思维能力 1 第 四 内点法 理解与掌握 9 面授 1 次作业。培养学生独立 1,2,3

部分 内点法,并用 证明相关思考能力和条 内点法解决 的理论问理清晰的思维 中规模问题 题,能够实方式 现内点法 注1:建议按照教学周周学时编排,以便自动生成教学日历。 注2:相应章节的课程思政融入点根据实际情况填写。 (1)平时作业30分 (2)自学作业20分 *考核方式 (3)期末考试50分 (Grading) (4)可选课程项目分数可替换期未考试分数。 *教材或参考资 1. 讲义自编 2.参考教材: 料(Textbooks a.S.Boyd,L.Vandenberghe.Convex Optimization,Cambridge,2004 &Other b.J.Nocedal,S.J.Wright.Numerical Optimization,second edition,Springer,2006 Materials) 其它(More)】 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为300-500字;课程大纲以表述清楚教学安排为宜,字数不限
部分 内点法,并用 内点法解决 中规模问题 证明相关 的理论问 题,能够实 现内点法 思考能力和条 理清晰的思维 方式 注 1:建议按照教学周周学时编排,以便自动生成教学日历。 注 2:相应章节的课程思政融入点根据实际情况填写。 *考核方式 (Grading) (1)平时作业 30 分 (2)自学作业 20 分 (3)期末考试 50 分 (4)可选课程项目分数可替换期末考试分数。 *教材或参考资 料 (Textbooks & Other Materials) 1. 讲义自编 2. 参考教材: a. S. Boyd, L. Vandenberghe.Convex Optimization, Cambridge, 2004 b. J. Nocedal, S. J. Wright. Numerical Optimization, second edition, Springer, 2006 其它(More) 备注(Notes) 备注说明: 1.带*内容为必填项。 2.课程简介字数为 300-500 字;课程大纲以表述清楚教学安排为宜,字数不限