
《高等数学》课程教学大纲 课程名称:高等数学 课程类别:专业基础课 适用专业:教育技术、心理学 考核方式:考试 总学时、学分:48学时、3学分 其中实验学时:0学时 一、课程教学目的 高等数学(本科少学时)是对数学要求不高的专业学生的一门基 础理论课,它是为培养我国社会主义现代化建设所需要的高质量专 门人才服务的。 通过本课程的学习,要使学生获得:1.集合有关知识:2.函数与 极限;3.一元函数微积分学的基本概念、基本理论和基本运算技能。 在传授知识的同时,要通过各个教学环节逐步培养学生抽象思维 能力、逻辑推理能力、空间想象能力、运算能力、自学能力和辩证的 思考能力,还要特别注意培养学生具有综合运用所学知识去分析问题 和解决问题的能力。为学生学习后续课程和进一步获得近代科学技术 知识奠定必要的数学基础。 二、课程教学要求 1.掌握本课程的基本内容。掌握极限的概念,熟练掌握两个重要 的极限;理解并掌握导数与微分的概念,并了解他们的几何意义;理 解原函数和不定积分的概念;理解掌握定积分的定义及其几何意义。 2.能熟练进行基本计算。能运用四则运算、两边夹定理、两个重 要极限及洛必达法则熟练的求极限:能熟练的应用求导法则(尤其是 复合函数求导法则)求函数的导数;能熟练的求函数的微分;熟练掌 握牛顿-莱布尼兹公式及换元积分法和分部积分法
《高等数学》课程教学大纲 课程名称:高等数学 课程类别:专业基础课 适用专业:教育技术、心理学 考核方式:考试 总学时、学分:48 学时、3 学分 其中实验学时:0 学时 一、 课程教学目的 高等数学(本科少学时)是对数学要求不高的专业学生的一门基 础理论课,它是为培养我国社会主义现代化建设所需要的高质量专 门人才服务的。 通过本课程的学习,要使学生获得:1.集合有关知识;2.函数与 极限;3.一元函数微积分学的基本概念、基本理论和基本运算技能。 在传授知识的同时,要通过各个教学环节逐步培养学生抽象思维 能力、逻辑推理能力、空间想象能力、运算能力、自学能力和辩证的 思考能力,还要特别注意培养学生具有综合运用所学知识去分析问题 和解决问题的能力。为学生学习后续课程和进一步获得近代科学技术 知识奠定必要的数学基础。 二、 课程教学要求 1.掌握本课程的基本内容。掌握极限的概念,熟练掌握两个重要 的极限;理解并掌握导数与微分的概念,并了解他们的几何意义;理 解原函数和不定积分的概念;理解掌握定积分的定义及其几何意义。 2.能熟练进行基本计算。能运用四则运算、两边夹定理、两个重 要极限及洛必达法则熟练的求极限;能熟练的应用求导法则(尤其是 复合函数求导法则)求函数的导数;能熟练的求函数的微分;熟练掌 握牛顿-莱布尼兹公式及换元积分法和分部积分法

3.能应用微积分的方法解决一定范围的实际问题。会求函数的极 值和最大(小)值及简单应用问题能用导数较正确的做出函数图象。 4.在讲授本课程知识及其应用的同时,注重向学生渗透数学思想 方法,使学生了解数学观点及思维方式,了解本课程的知识体系,养 成科学思考的习惯;注重向学生渗透数学史及数学家的相关内容,从 而提高学习数学的兴趣。 三、先修课程 初等数学 四、课程教学重、难点 重点:极限概念,极限的四则运算法则:导数、微分概念,初等 函数导数的求解:函数的单调性求解:不定积分与定积分的换元积分 法和分部积分法; 难点:数列极限与函数极限的概念;复合函数、隐函数的求导; 定积分与不定积分的换元积分法与分部积分法。 五、课程教学方法与教学手段 传统教学方法和现代教学手段结合,尽量多使用多媒体教学等现 代教学手段。 六、课程教学内容 第一章 函数和极限(12学时) 1.教学内容 (1)函数: (2)数列的极限: (3)函数的极限:
3.能应用微积分的方法解决一定范围的实际问题。会求函数的极 值和最大(小)值及简单应用问题能用导数较正确的做出函数图象。 4.在讲授本课程知识及其应用的同时,注重向学生渗透数学思想 方法,使学生了解数学观点及思维方式,了解本课程的知识体系,养 成科学思考的习惯;注重向学生渗透数学史及数学家的相关内容,从 而提高学习数学的兴趣。 三、 先修课程 初等数学 四、 课程教学重、难点 重点:极限概念,极限的四则运算法则;导数、微分概念,初等 函数导数的求解;函数的单调性求解;不定积分与定积分的换元积分 法和分部积分法; 难点:数列极限与函数极限的概念;复合函数、隐函数的求导; 定积分与不定积分的换元积分法与分部积分法。 五、 课程教学方法与教学手段 传统教学方法和现代教学手段结合,尽量多使用多媒体教学等现 代教学手段。 六、 课程教学内容 第一章 函数和极限(12 学时) 1.教学内容 (1)函数; (2)数列的极限; (3)函数的极限;

(4)无穷小和无穷大: (⑤)极限运算法则: (6)极限存在准则,两个重要极限: (7)无穷小比较: (8)函数的连续性: (9)闭区间上连续函数的性质。 2.重、难点提示 (1)重点:函数的概念,函数的奇偶性、单调性、有界性和周期性,反函数和复合函数 的定义及其性质,基本初等函数的图形及其简单性质:数列和函数极限,极限的四则运算法 则及其应用,两个重要极限及其应用,连续与间断,连续函数的四则运算法则和反函数及复 合函数的连续性,闭区间上的连续函数: (2)难点:建立函数关系,函数的有界性,求复合函数的定义域,基本初等函数的图形 及其简单性质.根据定义求极限,极限的四则运算法则,两个重要极限的应用,判断间断点 和反函数及复合函数的连续性,闭区间上的连续函数。 第二章导数与微分(10学时) 1.教学内容 (1)导数的概念: (2)函数的和、积、商的求导法则: (3)反函数和复合函数求导法则: (4)高阶导数: (5)隐函数的导数以及由参数方程所确定的函数的导数: (6)函数的微分。 2.重、难点提示 (1)重点:导数、微分概念,导数的几何意义,复合函数的求导法则,高阶导数的求 导法则:隐函数的导数以及由参数方程所确定的函数的导数: (2)难点:导数的概念,复合函数、隐函数求导法则,高阶导数的求导法则。 第三章中值定理与导数的应用(8学时) 1.教学内容 (1)中值定理:
(4)无穷小和无穷大; (5)极限运算法则; (6)极限存在准则,两个重要极限; (7)无穷小比较; (8)函数的连续性; (9)闭区间上连续函数的性质。 2.重、难点提示 (1) 重点:函数的概念,函数的奇偶性、单调性、有界性和周期性,反函数和复合函数 的定义及其性质,基本初等函数的图形及其简单性质;数列和函数极限,极限的四则运算法 则及其应用,两个重要极限及其应用,连续与间断,连续函数的四则运算法则和反函数及复 合函数的连续性,闭区间上的连续函数; (2)难点:建立函数关系,函数的有界性,求复合函数的定义域,基本初等函数的图形 及其简单性质.根据定义求极限,极限的四则运算法则,两个重要极限的应用,判断间断点 和反函数及复合函数的连续性,闭区间上的连续函数。 第二章 导数与微分(10 学时) 1.教学内容 (1)导数的概念; (2)函数的和、积、商的求导法则; (3)反函数和复合函数求导法则; (4)高阶导数; (5)隐函数的导数以及由参数方程所确定的函数的导数; (6)函数的微分。 2.重、难点提示 (1) 重点:导数、微分概念,导数的几何意义,复合函数的求导法则,高阶导数的求 导法则;隐函数的导数以及由参数方程所确定的函数的导数; (2)难点:导数的概念,复合函数、隐函数求导法则,高阶导数的求导法则。 第三章 中值定理与导数的应用(8 学时) 1.教学内容 (1)中值定理;

(2)洛必达法则: (3)泰勒中值定理: (4)函数的单调性和曲线的凹凸性: (5)函数的极性和最大、最小值: (6)函数图像的描绘。 2.重、难点提示 (1)重点:中值定理的内容及意义,洛必塔法则,用导数判断函数的单调性,凹凸性, 求函数的极值和最值,函数图像的描绘: (2)难点:中值定理的应用,理解洛必达法则失效的情况,极值的概念。 第四章 不定积分(8学时) 1.教学内容 (1)不定积分的概念和性质: (2)换元积分法: (3)与分部积分法: (4)有理函数的不定积分。 2.重、难点提示 (1)重点:原函数与不定积分的概念,基本积分表,不定积分的性质,不定积分的换元 积分法与分部积分法有理函数的不定积分: (2)难点:不定积分的换元积分法和分部积分法。 第五章 定积分及其应用(10学时) 1.教学内容 (1)定积分的概念与性质: (2)微积分基本公式: (3)定积分的换元法与分部积分法: (4)定积分在几何上的应用: (5)定积分在物理上的应用。 2.重、难点提示 (1)重点:定积分概念,变上限函数及其求导定理,牛顿-莱布尼茨公式,微元法和几 何应用:
(2)洛必达法则; (3)泰勒中值定理; (4)函数的单调性和曲线的凹凸性; (5)函数的极性和最大、最小值; (6)函数图像的描绘。 2.重、难点提示 (1)重点:中值定理的内容及意义,洛必塔法则,用导数判断函数的单调性,凹凸性, 求函数的极值和最值,函数图像的描绘; (2)难点:中值定理的应用,理解洛必达法则失效的情况,极值的概念。 第四章 不定积分(8 学时) 1.教学内容 (1)不定积分的概念和性质; (2)换元积分法; (3)与分部积分法; (4)有理函数的不定积分。 2.重、难点提示 (1)重点:原函数与不定积分的概念,基本积分表,不定积分的性质,不定积分的换元 积分法与分部积分法;有理函数的不定积分; (2)难点:不定积分的换元积分法和分部积分法。 第五章 定积分及其应用(10 学时) 1.教学内容 (1)定积分的概念与性质; (2)微积分基本公式; (3)定积分的换元法与分部积分法; (4)定积分在几何上的应用; (5)定积分在物理上的应用。 2.重、难点提示 (1)重点:定积分概念,变上限函数及其求导定理,牛顿–莱布尼茨公式,微元法和几 何应用;
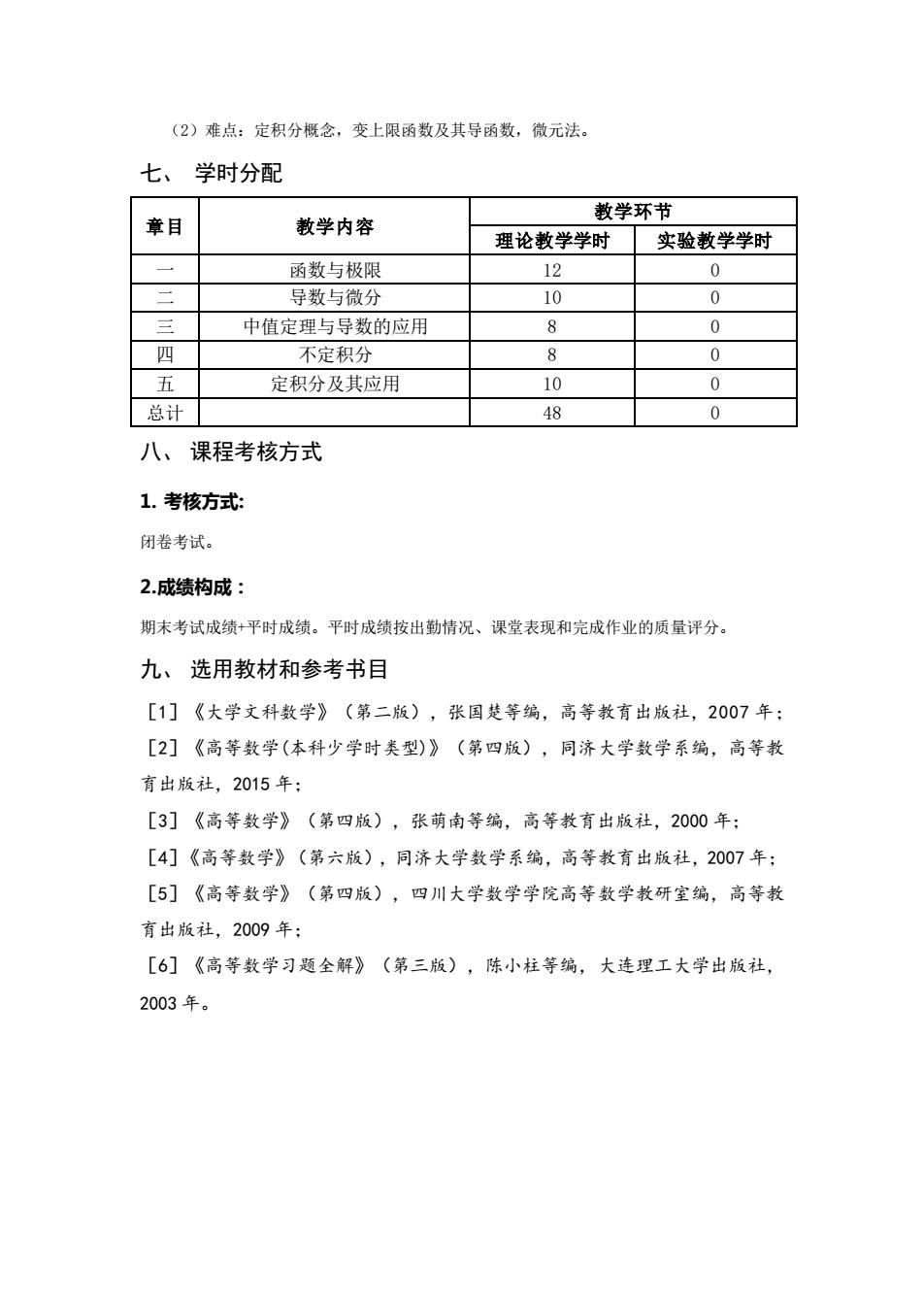
(2)难点:定积分概念,变上限函数及其导函数,微元法。 七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 一 函数与极限 12 0 二 导数与微分 10 0 三 中值定理与导数的应用 8 0 四 不定积分 P 0 五 定积分及其应用 10 0 总计 48 0 八、课程考核方式 1.考核方式 闭卷考试。 2.成绩构成: 期末考试成绩+平时成绩。平时成绩按出勤情况、课堂表现和完成作业的质量评分。 九、选用教材和参考书目 [1]《大学文科数学》(第二版),张国楚等编,高等教育出版社,2007年: [2]《高等数学(本科少学时类型)》(第四版),同济大学数学系编,高等教 育出版社,2015年: [3]《高等数学》(第四版),张萌南等编,高等教育出版社,2000年: [4]《高等数学》(第六版),同济大学数学系编,高等教育出版社,2007年: [5]《高等数学》(第四版),四川大学数学学院高等数学教研室编,高等教 育出版社,2009年; [6]《高等数学习题全解》(第三版),陈小柱等编,大连理工大学出版社, 2003年
(2)难点:定积分概念,变上限函数及其导函数,微元法。 七、 学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 函数与极限 12 0 二 导数与微分 10 0 三 中值定理与导数的应用 8 0 四 不定积分 8 0 五 定积分及其应用 10 0 总计 48 0 八、 课程考核方式 1. 考核方式: 闭卷考试。 2.成绩构成: 期末考试成绩+平时成绩。平时成绩按出勤情况、课堂表现和完成作业的质量评分。 九、 选用教材和参考书目 [1]《大学文科数学》(第二版),张国楚等编,高等教育出版社,2007 年; [2]《高等数学(本科少学时类型)》(第四版),同济大学数学系编,高等教 育出版社,2015 年; [3]《高等数学》(第四版),张萌南等编,高等教育出版社,2000 年; [4]《高等数学》(第六版),同济大学数学系编,高等教育出版社,2007 年; [5]《高等数学》(第四版),四川大学数学学院高等数学教研室编,高等教 育出版社,2009 年; [6]《高等数学习题全解》(第三版),陈小柱等编,大连理工大学出版社, 2003 年
