
《心理统计川》课程教学大纲 一、课程基本信息 课程代码:16107203 课程名称:心理统计Ⅱ 英文名称:Psychological Statistics IⅡ 课程类别:学科基础课 学 时:48 学 分:3 适用对象:应用心理学专业 者核方式:考试 先修课程:心理统计I 二、课程简介 心理统计课程介绍了当今心理学研究中主要的统计方法,内容包括:描述统 计(样本的数据特征和统计图表),概率基础知识,随机变量及其分布,参数点估 计和区间估计,参数假设检验,分布检验,变量独立性检验,效应量和检验力, 各种变量的相关分析,测量信度,一元和多元回归分析,单因素、多因素方差分 析和重复测量实验设计的方差分析,一元逻辑斯蒂回归分析,因子分析和主成分 分析。重点讨论了统计思想和统计原理、应用实例、SPSS软件操作方法、结果 解释和表述。 Psychological Statistics introduces the main statistical methods of present psychological research.It covers:descriptive statistics(data features of samples and diagrams),basic knowledge of probability,random variables and their distribution, parameter point estimation and interval estimation,parametric hypothesis test, distribution test,variable independence test.effect size and power of statistical test. analysis of various variables,test reliability,univariate and multivariate regression analysis,one-way ANOVA(analysis of variance),multivariate ANOVA,repeated measures ANOVA,unary logistic regression analysis,factor analysis and principal component analysis.This course focuses on statistical ideas and principles, application cases,operation of software SPSS,result interpretation and expression. 三、课程性质与教学目的 本课程的性质是“学科基础课” 教学目的是,通过本门课程的教学活动,使学生学握回归分析、方差分析、 因子分析等统计分析方法的统计思想、原理和实际操作步骤,以及统计结果的解
《心理统计Ⅱ》课程教学大纲 一、 课程基本信息 课程代码:16107203 课程名称:心理统计Ⅱ 英文名称:Psychological Statistics Ⅱ 课程类别:学科基础课 学 时: 48 学 分: 3 适用对象: 应用心理学专业 考核方式:考试 先修课程:心理统计 I 二、 课程简介 心理统计课程介绍了当今心理学研究中主要的统计方法,内容包括:描述统 计(样本的数据特征和统计图表),概率基础知识,随机变量及其分布,参数点估 计和区间估计,参数假设检验,分布检验,变量独立性检验,效应量和检验力, 各种变量的相关分析,测量信度,一元和多元回归分析,单因素、多因素方差分 析和重复测量实验设计的方差分析,一元逻辑斯蒂回归分析,因子分析和主成分 分析。重点讨论了统计思想和统计原理、应用实例、SPSS 软件操作方法、结果 解释和表述。 Psychological Statistics introduces the main statistical methods of present psychological research. It covers: descriptive statistics (data features of samples and diagrams), basic knowledge of probability, random variables and their distribution, parameter point estimation and interval estimation, parametric hypothesis test, distribution test, variable independence test, effect size and power of statistical test, analysis of various variables, test reliability, univariate and multivariate regression analysis, one-way ANOVA(analysis of variance), multivariate ANOVA, repeated measures ANOVA, unary logistic regression analysis, factor analysis and principal component analysis. This course focuses on statistical ideas and principles, application cases, operation of software SPSS, result interpretation and expression. 三、课程性质与教学目的 本课程的性质是“学科基础课”。 教学目的是,通过本门课程的教学活动,使学生掌握回归分析、方差分析、 因子分析等统计分析方法的统计思想、原理和实际操作步骤,以及统计结果的解

释和表述,为学生从事心理学研究、毕业论文创作、以及毕业后从事相关工作时, 能熟练使用统计方法分析相关的数据。 四、教学内容及要求 第八章相关分析 (一)目的与要求 使学生了解相关的概念和特点,掌握如何计算person相关系数,用于 检验两个类别变量独立性的列联表分析,以及信度测量。 (二)教学内容 第一节相关系数 1、主要内容:相关分析 2、基本概念与知识点: 1)、相关:一个变量的值发生了变化,另一个变量的值也发生变化,这种共 同变化的关系,统计上称为相关。 正相关是指一个变量的值增加时,另一个变量的值也有增加的趋势。如入学 时英语词汇量与第一学年末词汇量的相关就是正相关的例子,入学时词汇量越 多,第一学年末词汇量也越多。如果检验结果是两次测验的词汇量相关显著,在 写研究报告时,在给出相关系数及其显著性概率后,通常会说:“第一学年末词 汇量与入学时词汇量有显著正相关,即入学时词汇量越多,第一学年末的词汇量 往往也越多”。 负相关是指一个变量的值增加时,另一个变量的值反而有成少的趋势。例如, 被试人格因素中的外向性和神经质的相关,外向性得分越高的被试,神经质的得 分有降低的趋势,即外向性与神经质负相关。如果检验结果是外向性和神经质相 关显著,在写研究报告时,可以这样说:“外向性和神经质负相关显著。一般地 说,外向性得分越高的被试,神经质得分越低。外向性得分越低的被试,神经质 得分越高”。 2)、相关系数的特性 对称性:如果计算相关系数时不需要区分哪个是自变量(independent variable),哪个是因变量(dependent variable),这样的相关系数描述了对称 (symmetrical)关系, 3)、相关系数 用来描述两个变量相互之间变化方向及密切程度的数字特征量称为相关系 数。一般用「表示。相关系数的值,仅仅是一个比值。它不是由相等单位度量而 来(即不等距),也不是百分比,因此,不能直接作加、减、乘、除。相关系数 只能描述两个变量之间的变化方向及密切程度,并不能揭示二者之间的内在本质 联系。相关系数的值在-1和+1之间,0相关意味着没有关系,+1意味着"完 全的正相关"之间两个,1意味着完全的负相关。 4)、皮尔逊相关
释和表述,为学生从事心理学研究、毕业论文创作、以及毕业后从事相关工作时, 能熟练使用统计方法分析相关的数据。 四、教学内容及要求 第八章 相关分析 (—) 目的与要求 使学生了解相关的概念和特点,掌握如何计算 person 相关系数,用于 检验两个类别变量独立性的列联表分析,以及信度测量。 (二)教学内容 第一节 相关系数 1、主要内容:相关分析 2、基本概念与知识点: 1)、相关:一个变量的值发生了变化,另一个变量的值也发生变化,这种共 同变化的关系,统计上称为相关。 正相关是指一个变量的值增加时,另一个变量的值也有增加的趋势。如入学 时英语词汇量与第一学年末词汇量的相关就是正相关的例子,入学时词汇量越 多,第一学年末词汇量也越多。如果检验结果是两次测验的词汇量相关显著,在 写研究报告时,在给出相关系数及其显著性概率后,通常会说:“第一学年末词 汇量与入学时词汇量有显著正相关,即入学时词汇量越多,第一学年末的词汇量 往往也越多”。 负相关是指一个变量的值增加时,另一个变量的值反而有减少的趋势。例如, 被试人格因素中的外向性和神经质的相关,外向性得分越高的被试,神经质的得 分有降低的趋势,即外向性与神经质负相关。如果检验结果是外向性和神经质相 关显著,在写研究报告时,可以这样说:“外向性和神经质负相关显著。一般地 说,外向性得分越高的被试,神经质得分越低。外向性得分越低的被试,神经质 得分越高”。 2)、相关系数的特性 对称性:如果计算相关系数时不需要区分哪个是自变量(independent variable),哪个是因变量(dependent variable),这样的相关系数描述了对称 (symmetrical)关系。 3)、相关系数 用来描述两个变量相互之间变化方向及密切程度的数字特征量称为相关系 数。一般用 r 表示。相关系数的值,仅仅是一个比值。它不是由相等单位度量而 来(即不等距),也不是百分比,因此,不能直接作加、减、乘、除。相关系数 只能描述两个变量之间的变化方向及密切程度,并不能揭示二者之间的内在本质 联系。相关系数的值在-1 和 +1 之间,0 相关意味着没有关系,+1 意味着"完 全的正相关" 之间两个,-1 意味着完全的负相关。 4)、皮尔逊相关

一个变量是定距变量,一个变量是二值变量,将后者编码为0和1,然后计 算皮尔逊相关系数,就等于点双列相关系数。 X与Y是两个特殊的定序变量,各有相同的等级个数,每个样品的变量值是 样本排序后该样品的等级值,计算皮尔逊相关系数,就等于斯皮尔曼等级相关系 数。 第二节列联表分析和独立性检验 1、主要内容:独立性检验 2、基本概念与知识点: 1)定义: 如果两个变量X和Y都是定类变量,根据这两个题目的答案可得列联表。 列联表分析要研究的问题是,两个定类变量之间有关吗? 2)列联表检验的过程: 3)x2检验的意义: A、检验一个类别变量的分布是否服从一个假设的分布(如均匀分布) B、检验两个类别变量之间是否相关 第三节测验信度 1、主要内容:测验信度 2、基本概念与知识点: 1)定义:测验信度是指测验结果的一致性或稳定性程度。 2)重测信度:是同一组被试使用同一份试题(以及相同的评分标准),前后两 次测验分数的相关系数 3)复本信度:是用两份“等值”(内容、题型、题数、难度等都相同或非常接 近)但具体题目又不同的两份试题,相继对同一组被试进行两次测验所得分数的 相关系数。 4)分半信度:把一个测验中的题目按编号分成两半,分别计算出每个被试两 部分的得分。然后计算这两个部分的相关系数 5)评分者信度:又称斯皮尔曼等级相关系数,是度量两个等级变量的相关系 数,肯德尔和谐系数是度量多个等级变量的相关系数 6)a系数:Alpha系数又称为Cronbach系数,它等于一个测验的所有可能的 分半信度的平均值 题目个数会影响a系数。一般来说,增加题目,α系数通常会变大。 ā系数既不能用来衡量测验的内部一致性,也不能用来衡量测验的同质性 如果一份量表由多个分量表组成,只需要计算和报告分量表的ā系数,计算 和报告总量表的系数没有多大意义。 (三)思考与实践 思考:本章内容的相关分析是描述性统计的内容,比较简单,但却 是下一章回归分析的基础。另外,本章十分重要的是信度分析方法,这是问卷调 查研究十分重要的部分
一个变量是定距变量,一个变量是二值变量,将后者编码为 0 和 1,然后计 算皮尔逊相关系数,就等于点双列相关系数。 X 与 Y 是两个特殊的定序变量,各有相同的等级个数,每个样品的变量值是 样本排序后该样品的等级值,计算皮尔逊相关系数,就等于斯皮尔曼等级相关系 数。 第二节 列联表分析和独立性检验 1、主要内容:独立性检验 2、基本概念与知识点: 1)定义: 如果两个变量 X 和 Y 都是定类变量,根据这两个题目的答案可得列联表。 列联表分析要研究的问题是,两个定类变量之间有关吗? 2)列联表检验的过程: 3)x 2 检验的意义: A、检验一个类别变量的分布是否服从一个假设的分布(如均匀分布) B、检验两个类别变量之间是否相关 第三节 测验信度 1、主要内容:测验信度 2、基本概念与知识点: 1)定义:测验信度是指测验结果的一致性或稳定性程度。 2)重测信度:是同一组被试使用同一份试题(以及相同的评分标准),前后两 次测验分数的相关系数 3)复本信度:是用两份“等值”(内容、题型、题数、难度等都相同或非常接 近)但具体题目又不同的两份试题,相继对同一组被试进行两次测验所得分数的 相关系数。 4)分半信度:把一个测验中的题目按编号分成两半,分别计算出每个被试两 部分的得分。然后计算这两个部分的相关系数 5)评分者信度:又称斯皮尔曼等级相关系数,是度量两个等级变量的相关系 数,肯德尔和谐系数是度量多个等级变量的相关系数。 6)α系数:Alpha 系数又称为 Cronbach 系数,它等于一个测验的所有可能的 分半信度的平均值。 题目个数会影响α系数。一般来说,增加题目,α系数通常会变大。 α系数既不能用来衡量测验的内部一致性,也不能用来衡量测验的同质性。 如果一份量表由多个分量表组成,只需要计算和报告分量表的α系数,计算 和报告总量表的α系数没有多大意义。 (三) 思考与实践 思考:本章内容的相关分析是描述性统计的内容,比较简单,但却 是下一章回归分析的基础。另外,本章十分重要的是信度分析方法,这是问卷调 查研究十分重要的部分

实践环节:相关分析的SPSS操作 课后练习:P164-1661-7题 (四)教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第九章回归分析 (一)目的与要求 使学生了解和掌握线性回归,包括一个自变量和多个自变量的线性回归。掌 握如何建立回归方程、如何检验、评价和解释回归方程,如何利用回归方程进行 预测。从回归分析的教学中,让学生知道回归分析和方差分析是可以互通的,换 句话说,让学生感受到学科之间并没有绝对的界限,现在的科学发展的一个趋势 就是学科交叉。 (二)教学内容 第一节一元线性回归 1、主要内容:一元线性回归的原理与计算 2、基本概念与知识点: 1)作用和意义: 如果两个变量X和Y的相关显著,说明这两个变量有某种程度的共变关系 我们希望通过x的值去预测Y的值,或者希望了解Y的变化在多大程度上可以由 X的变化来解释。这时,称Y为因变量(dependent variable),X为自变量 (independent variable)或预测变量。 作回归分析就是试图找到一条直线(以及线性方程)以最佳地拟合数据点。最 佳拟合线意味着:目标是是使误差最小。即,这条线与所有的数据点最近,是最 佳拟合线。回归线是给定X,a和b,用公式(线性方程)来预测Y的值。我们 的目标是找出一条线,以对Y作最佳估计.即,这条线使得所有Y值的估计误 差最小 2)一元线性回归的过程: A、一元线性回归是指只有一个自变量的线性回归。 B、拟合直线的方法:最小二乘法 C、回归方程的显著性检验:方差分析法 D、回归系数的显著性检验:t检验 E、回归方程的预测作用: F、回归方程的解释作用:测定系数指回归平方和在总平方和中所占比例, 这个比例越大,意味着误差平方和所占比例越小,预测效果就越好。测定系数同 时等于相关系数的平方」 3)一元线性回归方程检验有三种等效的方法: a、对回归方程进行方差分析 b、对两个变量的相关系数进行与总体零相关的显著性检验
实践环节:相关分析的 SPSS 操作 课后练习:P164-166 1-7 题 (四) 教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第九章 回归分析 (一)目的与要求 使学生了解和掌握线性回归,包括一个自变量和多个自变量的线性回归。掌 握如何建立回归方程、如何检验、评价和解释回归方程,如何利用回归方程进行 预测。从回归分析的教学中,让学生知道回归分析和方差分析是可以互通的,换 句话说,让学生感受到学科之间并没有绝对的界限,现在的科学发展的一个趋势 就是学科交叉。 (二)教学内容 第一节 一元线性回归 1、主要内容:一元线性回归的原理与计算 2、基本概念与知识点: 1)作用和意义: 如果两个变量 X 和 Y 的相关显著,说明这两个变量有某种程度的共变关系。 我们希望通过 X 的值去预测 Y 的值,或者希望了解 Y 的变化在多大程度上可以由 X 的变化来解释。这时,称 Y 为因变量(dependent variable),X 为自变量 (independent variable)或预测变量。 作回归分析就是试图找到一条直线(以及线性方程)以最佳地拟合数据点。最 佳拟合线意味着:目标是是使误差最小。即,这条线与所有的数据点最近,是最 佳拟合线。回归线是给定 X,a 和 b,用公式 (线性方程)来预测 Y 的值。我们 的目标是找出一条线,以对 Y 作最佳估计. 即,这条线使得所有 Y 值的估计误 差最小。 2)一元线性回归的过程: A、一元线性回归是指只有一个自变量的线性回归。 B、拟合直线的方法:最小二乘法 C、回归方程的显著性检验:方差分析法 D、回归系数的显著性检验:t 检验 E、回归方程的预测作用: F、回归方程的解释作用:测定系数指回归平方和在总平方和中所占比例, 这个比例越大,意味着误差平方和所占比例越小,预测效果就越好。测定系数同 时等于相关系数的平方。 3)一元线性回归方程检验有三种等效的方法: a、对回归方程进行方差分析 b、对两个变量的相关系数进行与总体零相关的显著性检验

c、对回归系数进行显著性检验 4)可线性化的曲线回▣归 先做数据变换,然后对变换后的数据做直线回归分析,再将结果变换回曲线 方程。 第二节多元线性回归 1、主要内容:多元线性回归的原理与计算 2、基本概念与知识点: 1)多元回归方程 a)多元线性回归方程是指Y对X1、X2。。知的线性回归方程。 b)多元线性回归方程的建立原理和一元线性回归方程一样,多元线性回 归方程也用最小二乘法来确定回归系数。 c)多元线性标准回归方程为了比较多个自变量在估计预测因变量时所起 作用的大小,需要将所有变量分别转换成标准分数,然后比较由标准分 数所建立的标准回归方程中的多个标准回归系数,以此判断两个自变量 作用的大小 2)多元回归的检验 多元线性回归的检验包括两个方面:一是检验回归方程的显著性:另一是检 验两个偏回归系数的显著性。 3)、多元线性回归方程中自变量的选择 a)指定变量(enter) b)向后剔除法(backward) c)向前选择法(forward) d)逐步回归法(stepwise) 逐步回归的原理是按每个自变量对因变量的作用,从大到小逐个地引入回归 方程,每引入一个自变量要对回归方程中的每一个自变量都讲行显著性检验(即 对其偏回归系数进行显著性检验)。这样逐步地引入自变量,并剔除不显著的自 变量,直至将所有的自变量都引入,并将不显著的自变量都剔除为止,最后形成 的回归方程就是最优方程。 e)层次回归法:自变量进入方程的顺序是人为确定的 4、残差分析 误差方差齐性检验 相邻误差项是否有序列相关(Durbin-Watson检验) 误差正态性检验 查找异常点(outlier) 5)、额外平方和与2的变化 2的变化可以了解新加入的变量有多大作用 6)回归分析的四个前提条件:
c、对回归系数进行显著性检验 4)可线性化的曲线回归 先做数据变换,然后对变换后的数据做直线回归分析,再将结果变换回曲线 方程。 第二节 多元线性回归 1、主要内容:多元线性回归的原理与计算 2、基本概念与知识点: 1) 多元回归方程 a)多元线性回归方程是指 Y 对 X1 、X2。。。Xn 的线性回归方程。 b)多元线性回归方程的建立原理和一元线性回归方程一样,多元线性回 归方程也用最小二乘法来确定回归系数。 c)多元线性标准回归方程为了比较多个自变量在估计预测因变量时所起 作用的大小,需要将所有变量分别转换成标准分数,然后比较由标准分 数所建立的标准回归方程中的多个标准回归系数,以此判断两个自变量 作用的大小。 2) 多元回归的检验 多元线性回归的检验包括两个方面:一是检验回归方程的显著性;另一是检 验两个偏回归系数的显著性。 3)、多元线性回归方程中自变量的选择 a)指定变量(enter) b)向后剔除法(backward) c)向前选择法(forward) d)逐步回归法(stepwise) 逐步回归的原理是按每个自变量对因变量的作用,从大到小逐个地引入回归 方程,每引入一个自变量要对回归方程中的每一个自变量都进行显著性检验(即 对其偏回归系数进行显著性检验)。这样逐步地引入自变量,并剔除不显著的自 变量,直至将所有的自变量都引入,并将不显著的自变量都剔除为止,最后形成 的回归方程就是最优方程。 e)层次回归法:自变量进入方程的顺序是人为确定的 4)、残差分析 误差方差齐性检验 相邻误差项是否有序列相关(Durbin-Watson 检验) 误差正态性检验 查找异常点(outlier) 5)、额外平方和与 R 2 的变化 R 2 的变化可以了解新加入的变量有多大作用 6)回归分析的四个前提条件:

(三)思考与实践 思考:本章内容是问卷调查研究数据分析的核心部分,地位十分重 要,要让学生不仅熟悉理论,更要熟练操作,确保数据分析的准确性和可靠性 实践环节:回归分析的SPSS操作 课后练习:P199-2001-4题 (四)教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十章方差分析 (一)目的与要求 了解和掌握方差分析的基本原理和计算方法,会计算单因素完全随机方差 分析,重复测量方差分析,两因素完全随机设计,两因素混合设计的方差分析。 从方差分析的发展上,让学生感受到,科学永无止境。科学的最大意义就在于不 断的探索,不断在前人基础上前进。 (二)教学内容 第一节单因素方差分析 1、主要内容:单因素方差分析的原理与计算 2、基本概念与知识点: 1)基本概念: 所谓因素(factor),是由研究者掌握的、设想为原因的变量(自变量) 一种是由研究者主动操纵而变化的变量,如学习内容、教学方法、教学组织形式、 学习时间、刺激次数(或强度)、作业量、活动方式等另一种是研究者主动选 择而变化的变量,如性别、年级、智力、家庭背景等。 因素的每个取值称为因素的一个水平(level))。每个因素各取一个水平得 到一个水平组合,称为一个实验处理(treatment)。对于单因素实验,一个水平就 是一个处理。 方差分析的基本功能就在于它对多组平均数差异的显著性进行检验的作 用。组间差异对组内差异的比值越大,则各组平均数的差异就越明显。通过对组 间差异与组内差异比值的分析,来推断几个相应平均数差异的显著性,这就是方 差分析的逻辑 2)方差分析的三个前提条件: 前提条件1:总体正态分布 前提条件2:变异可加性 前提条件3:方差齐性 3)检验步骤: )提出假设:至少有两个总体平均数不相等。 b)选择检验统计量并计算其值:几组(组数至少等于3)测验分数假定是从 几个相应的正态总体中随机抽出的独立样本,故可用组间方差和组内
(三)思考与实践 思考:本章内容是问卷调查研究数据分析的核心部分,地位十分重 要,要让学生不仅熟悉理论,更要熟练操作,确保数据分析的准确性和可靠性。 实践环节:回归分析的 SPSS 操作 课后练习:P199-200 1-4 题 (四)教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十章 方差分析 (一)目的与要求 了解和掌握方差分析的基本原理和计算方法,会计算单因素完全随机方差 分析,重复测量方差分析,两因素完全随机设计,两因素混合设计的方差分析。 从方差分析的发展上,让学生感受到,科学永无止境。科学的最大意义就在于不 断的探索,不断在前人基础上前进。 (二)教学内容 第一节 单因素方差分析 1、主要内容:单因素方差分析的原理与计算 2、基本概念与知识点: 1)基本概念: 所谓因素(factor),是由研究者掌握的、设想为原因的变量(自变量), 一种是由研究者主动操纵而变化的变量,如学习内容、教学方法、教学组织形式、 学习时间、刺激次数(或强度)、作业量、活动方式等;另一种是研究者主动选 择而变化的变量,如性别、年级、智力、家庭背景等。 因素的每个取值称为因素的一个水平(level)。每个因素各取一个水平得 到一个水平组合,称为一个实验处理(treatment)。对于单因素实验,一个水平就 是一个处理。 方差分析的基本功能就在于它对多组平均数差异的显著性进行检验的作 用。组间差异对组内差异的比值越大,则各组平均数的差异就越明显。通过对组 间差异与组内差异比值的分析,来推断几个相应平均数差异的显著性,这就是方 差分析的逻辑。 2) 方差分析的三个前提条件: 前提条件 1:总体正态分布 前提条件 2:变异可加性 前提条件 3:方差齐性 3) 检验步骤: a) 提出假设:至少有两个总体平均数不相等。 b) 选择检验统计量并计算其值:几组(组数至少等于 3)测验分数假定是从 几个相应的正态总体中随机抽出的独立样本,故可用组间方差和组内

方差的F比值来检验五个总体平均数差异的显著性。下面分几步来求 F值:①计算平方和(一般用原始数据计算)、组间平方和、组内平 方和、总平方和:②计算自由度③求F比值。 c统计决断:查F值表,实际计算得的F=15.72>5.99,则P<0.01,于 是根据F检验统计决断规则,在0.01显著性水平上拒绝H0接受H1。 其结论为:至少有两所中学该年级学生的数学成绩有极其显著的差 异。为了便于表述和分析,需列方差分析表。 d)多重比较(multiple comparisons): 要知道具体哪些水平之间有差异, 有标准水平的比较、两两比较、线性对比。 4)效果量 效应量是衡量实验效果强度或者变量关联强度的指标,它不受样本容量大 小的影响(或者影响很小)统计显著性实际上是效果量和样本量共同作用的结果 因出,当统计显薯后还需要报告独立于样本量的效果品大小,效果量才是研究者 最关心的。 5)流程图: 主效应是否显著 显若且因素水平大于2 不 多重比较 分析结束 第二节两因素完全随机方差分析 1、主要内容:两因素完全随机方差分析的原理与计算 2、基本概念与知识点: )功能:多因素方差分析不仅可以检验各个因素对因变量作用的显著性, 而且还可以检验因素与因素间共同结合对因变量发生交互作用的显著性。 2)定义:自变量有两个或以上水平的因素设计 3)平方和分解:SS总=SSA+SSB+SSAB+SSE 4)自由度分解:df总=dfA+dfB+dfAB+dfE 5)三个F比率可以表达为:①FA的主效应=A的主效应方差/误差方差: ②F的主效应=B的主效应方差/误差方差:③F4xFB=AxB交互作用/误差方 差。 6)交互效应分析 简单主效应的检验应当在交互效应显著的基出上进行。当交互效应显著时 (例如,方法和中介效应b的交互效应显著),以检验方法的简单主效应为例,简
方差的 F 比值来检验五个总体平均数差异的显著性。下面分几步来求 F 值:①计算平方和(一般用原始数据计算)、组间平方和、组内平 方和、总平方和;②计算自由度;③求 F 比值。 c) 统计决断:查 F 值表,实际计算得的 F=15.72>5.99 ,则 P<0.01 ,于 是根据 F 检验统计决断规则,在 0.01 显著性水平上拒绝 H0 接受 H1。 其结论为:至少有两所中学该年级学生的数学成绩有极其显著的差 异。为了便于表述和分析,需列方差分析表。 d) 多重比较(multiple comparisons): 要知道具体哪些水平之间有差异, 有标准水平的比较、两两比较、线性对比。 4)效果量 效应量是衡量实验效果强度或者变量关联强度的指标, 它不受样本容量大 小的影响(或者影响很小)。统计显著性实际上是效果量和样本量共同作用的结果, 因此,当统计显著后还需要报告独立于样本量的效果量大小,效果量才是研究者 最关心的。 5)流程图: 第二节 两因素完全随机方差分析 1、主要内容:两因素完全随机方差分析的原理与计算 2、基本概念与知识点: 1) 功能:多因素方差分析不仅可以检验各个因素对因变量作用的显著性, 而且还可以检验因素与因素间共同结合对因变量发生交互作用的显著性。 2) 定义:自变量有两个或以上水平的因素设计 3) 平方和分解: SS 总=SSA+SSB+SSAB+SSE 4) 自由度分解:df 总=dfA+dfB+dfAB+dfE 5) 三个 F 比率可以表达为: ①FA 的主效应= A 的主效应方差/误差方差; ②FB 的主效应= B 的主效应方差/误差方差;③F A×FB = A×B 交互作用/误差方 差。 6) 交互效应分析: 简单主效应的检验应当在交互效应显著的基础上进行。当交互效应显著时 (例如,方法和中介效应 ab 的交互效应显著),以检验方法的简单主效应为例,简
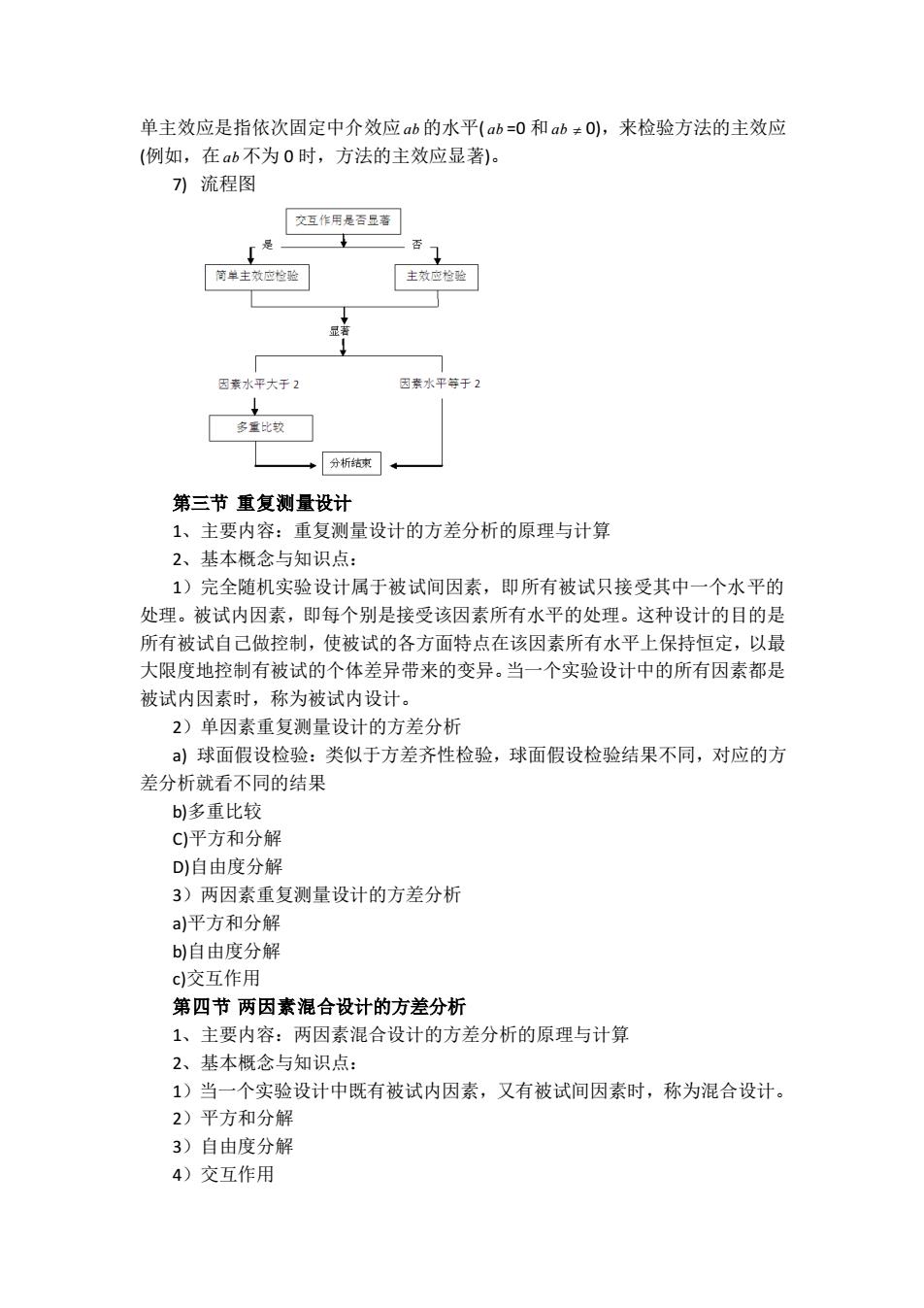
单主效应是指依次固定中介效应b的水平(ab=0和ab≠0,来检验方法的主效应 (例如,在ab不为0时,方法的主效应显著)。 )流程图 交互作用是香卫著 主效应验 多比较 第三节重复测量设计 1、主要内容:重复测量设计的方差分析的原理与计算 2、基本概念与知识点: 1)完全随机实验设计属于被试间因素,即所有被试只接受其中一个水平的 处理。被试内因素,即每个别是接受该因素所有水平的处理。这种设计的目的是 所有被试自己做控制,使被试的各方面特点在该因素所有水平上保持恒定,以最 大限度地控制有被试的个体差异带来的变异。当一个实验设计中的所有因素都是 被试内因素时,称为被试内设计。 2)单因素重复测量设计的方差分析 )球面假设检验:类似于方差齐性检验,球面假设检验结果不同,对应的方 差分析就看不同的结果 b)多重比较 C)平方和分解 D)自由度分解 3)两因素重复测量设计的方差分析 a)平方和分解 b)自由度分解 c)交互作用 第四节两因素混合设计的方差分析 1、主要内容:两因素混合设计的方差分析的原理与计算 2、基本概念与知识点: 1)当一个实验设计中既有被试内因素,又有被试间因素时,称为混合设计。 2)平方和分解 3)自由度分解 4)交互作用
单主效应是指依次固定中介效应 ab 的水平( ab =0 和 ab 0),来检验方法的主效应 (例如,在 ab 不为 0 时,方法的主效应显著)。 7) 流程图 第三节 重复测量设计 1、主要内容:重复测量设计的方差分析的原理与计算 2、基本概念与知识点: 1)完全随机实验设计属于被试间因素,即所有被试只接受其中一个水平的 处理。被试内因素,即每个别是接受该因素所有水平的处理。这种设计的目的是 所有被试自己做控制,使被试的各方面特点在该因素所有水平上保持恒定,以最 大限度地控制有被试的个体差异带来的变异。当一个实验设计中的所有因素都是 被试内因素时,称为被试内设计。 2)单因素重复测量设计的方差分析 a) 球面假设检验:类似于方差齐性检验,球面假设检验结果不同,对应的方 差分析就看不同的结果 b)多重比较 C)平方和分解 D)自由度分解 3)两因素重复测量设计的方差分析 a)平方和分解 b)自由度分解 c)交互作用 第四节 两因素混合设计的方差分析 1、主要内容:两因素混合设计的方差分析的原理与计算 2、基本概念与知识点: 1)当一个实验设计中既有被试内因素,又有被试间因素时,称为混合设计。 2)平方和分解 3)自由度分解 4)交互作用

(三)思老与实践 思考:本章内容是实验研究数据分析的核心部分,地位十分重要 要让学生不仅熟悉理论,更要熟练操作,确保数据分析的准确性和可靠性。 实践环节:方差分析的SPSs操作 课后练习:P235-2371-8题 (四)教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十一章Logistic回归 目的与要求 了解Logistic回归的原理和主要概念,熟悉Logistic回归分析的过程, 会解读Logistic回归分析的结果。 (二)教学内容 第一节一元Logistic回归分析 1、主要内容:一元Logistic回归分析的原理与计算 2、基本概念与知识点: 1)Logistic回归是处理因变量为分类变量的一种统计方法 2)一元Logistic回归模型 3)发生比(odds),定义为事件发生的概率P与事件不发生的概率1-P之 比,也称为成败比。 4)模型估计:ogistic回归不用最小二乘估计,而用极大似然估计。 5)回归系数的解释:发生比率>1时,发生比随X的增加而增加。 )模型检验:一2log-likelihood(缩写为一2LL),较小的一2L说明模型拟 合较好 7)回归系数的检验:通常使用Wald统计量对Logistic回归系数进行显著 性检验,称为Wald检验 8)伪测定系数:SPsS在Logistic回归估计结果中给出的是Cox&Snell R Square和Nagelkerke R Square.。前者是在似然函数值基础上模仿线性回归模型的 2来评价Logistic回归模型,但它的最大值往往小于1,解释时有困难。后者对 之做了调整,使得取值范围在0和1之间,比较容易解释。 第二节多元Logistic回归分析 1、主要内容:多元Logistic回归分析的原理与计算 2、基本概念与知识点: 1)多元Logistic回归模型 2)拟合优度检验:采用的是Hosmer-.Lemeshow拟合优度检验。如果P>a(如 ā=0.05),表明摸型对数据的拟合可以接受。 3)自变量的选择:SPSS中提供了7种筛选自变量的方法:1种是强迫进入
(三) 思考与实践 思考:本章内容是实验研究数据分析的核心部分,地位十分重要, 要让学生不仅熟悉理论,更要熟练操作,确保数据分析的准确性和可靠性。 实践环节:方差分析的 SPSS 操作 课后练习:P235-237 1-8 题 (四) 教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十一章 Logistic 回归 (一) 目的与要求 了解 Logistic 回归的原理和主要概念,熟悉 Logistic 回归分析的过程, 会解读 Logistic 回归分析的结果。 (二) 教学内容 第一节 一元 Logistic 回归分析 1、主要内容:一元 Logistic 回归分析的原理与计算 2、基本概念与知识点: 1)Logistic 回归是处理因变量为分类变量的一种统计方法 2)一元 Logistic 回归模型 3)发生比(odds),定义为事件发生的概率 P 与事件不发生的概率 1-P 之 比,也称为成败比。 4)模型估计:Logistic 回归不用最小二乘估计,而用极大似然估计。 5)回归系数的解释:发生比率>1 时,发生比随 X 的增加而增加。 6) 模型检验:-2log-likelihood(缩写为-2LL),较小的-2LL 说明模型拟 合较好。 7)回归系数的检验:通常使用 Wald 统计量对 Logistic 回归系数进行显著 性检验,称为 Wald 检验 8)伪测定系数:SPSS 在 Logistic 回归估计结果中给出的是 Cox & Snell R Square 和 Nagelkerke R Square。前者是在似然函数值基础上模仿线性回归模型的 R2 来评价 Logistic 回归模型,但它的最大值往往小于 1,解释时有困难。后者对 之做了调整,使得取值范围在 0 和 1 之间,比较容易解释。 第二节 多元 Logistic 回归分析 1、主要内容:多元 Logistic 回归分析的原理与计算 2、基本概念与知识点: 1)多元 Logistic 回归模型 2)拟合优度检验:采用的是 Hosmer-Lemeshow 拟合优度检验。如果 P>α(如 α=0.05),表明模型对数据的拟合可以接受。 3)自变量的选择:SPSS 中提供了 7 种筛选自变量的方法:1 种是强迫进入

法,3种属于向前选择法(类似于线性回归中的逐步回归法),另有3种属于向 后剔除法(类似于线性回归中的向后剔除法) (三)思考与实践 思考:本章内容是回归分析的进一步发展,要让学生不仅熟悉理论, 更要熟练操作,确保数据分析的准确性和可靠性, 实践环节:Logistic回归分析的SPSS操作 课后练习:P2551-3题 (四)教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十二章因子分析 (一)目的与要求 了解因子分析模型及其主要概念,熟悉因子分析的过程,会解读因 子分析的结果。 (二)教学内容 1、主要内容:因子分析的原理与计算 2、基本概念与知识点: 因子分析(factor analysis)是根据相关性大小把变量分组,使得同组内变量 之间的相关性较高,不同组之间的相关性较低。 每组变量对应于一个所谓的因子(factor)。在因子分析中,因子被认为是造 成该组变量变化的共同原因。从量表的角度看,因子是一组题目测量到的潜在特 质。 1)、因子分析模型: 正交因子模型假设:公共因子都是均值为0,方差为1的变量。特殊因 子的均值为0。各公共因子之间、特殊因子与公共因子之间、特殊因子与特殊因 子之间均为零相关,即它们之间的协方差(或相关系数)等于零。 2)、因子模型基本概念: 因子负荷:变量与因子的相关系数,反映了变量对因子的依赖程度,也 反映了变量对因子的相对重要性。 共同度:因子负荷矩阵各行的平方和 方差贡献:因子负荷矩阵各列的平方和 3)、因子分析步骤 a),计算相关矩阵 b).因子提取。 c).因子旋转。 d).计算因子得分。 e).对因子做出解释 4、因子模型估计方法
法,3 种属于向前选择法(类似于线性回归中的逐步回归法),另有 3 种属于向 后剔除法(类似于线性回归中的向后剔除法) (三) 思考与实践 思考:本章内容是回归分析的进一步发展,要让学生不仅熟悉理论, 更要熟练操作,确保数据分析的准确性和可靠性。 实践环节:Logistic 回归分析的 SPSS 操作 课后练习:P255 1-3 题 (四) 教学方法与手段 本章教学主要采用课堂讲授、课堂讨论、实践操作等 第十二章 因子分析 (一)目的与要求 了解因子分析模型及其主要概念,熟悉因子分析的过程,会解读因 子分析的结果。 (二)教学内容 1、主要内容:因子分析的原理与计算 2、基本概念与知识点: 因子分析(factor analysis)是根据相关性大小把变量分组,使得同组内变量 之间的相关性较高,不同组之间的相关性较低。 每组变量对应于一个所谓的因子(factor)。在因子分析中,因子被认为是造 成该组变量变化的共同原因。从量表的角度看,因子是一组题目测量到的潜在特 质。 1)、因子分析模型: 正交因子模型假设:公共因子都是均值为 0,方差为 1 的变量。特殊因 子的均值为 0。各公共因子之间、特殊因子与公共因子之间、特殊因子与特殊因 子之间均为零相关,即它们之间的协方差(或相关系数)等于零。 2)、因子模型基本概念: 因子负荷:变量与因子的相关系数,反映了变量对因子的依赖程度,也 反映了变量对因子的相对重要性。 共同度:因子负荷矩阵各行的平方和 方差贡献:因子负荷矩阵各列的平方和 3)、因子分析步骤: a). 计算相关矩阵。 b). 因子提取。 c). 因子旋转。 d). 计算因子得分。 e). 对因子做出解释。 4)、因子模型估计方法