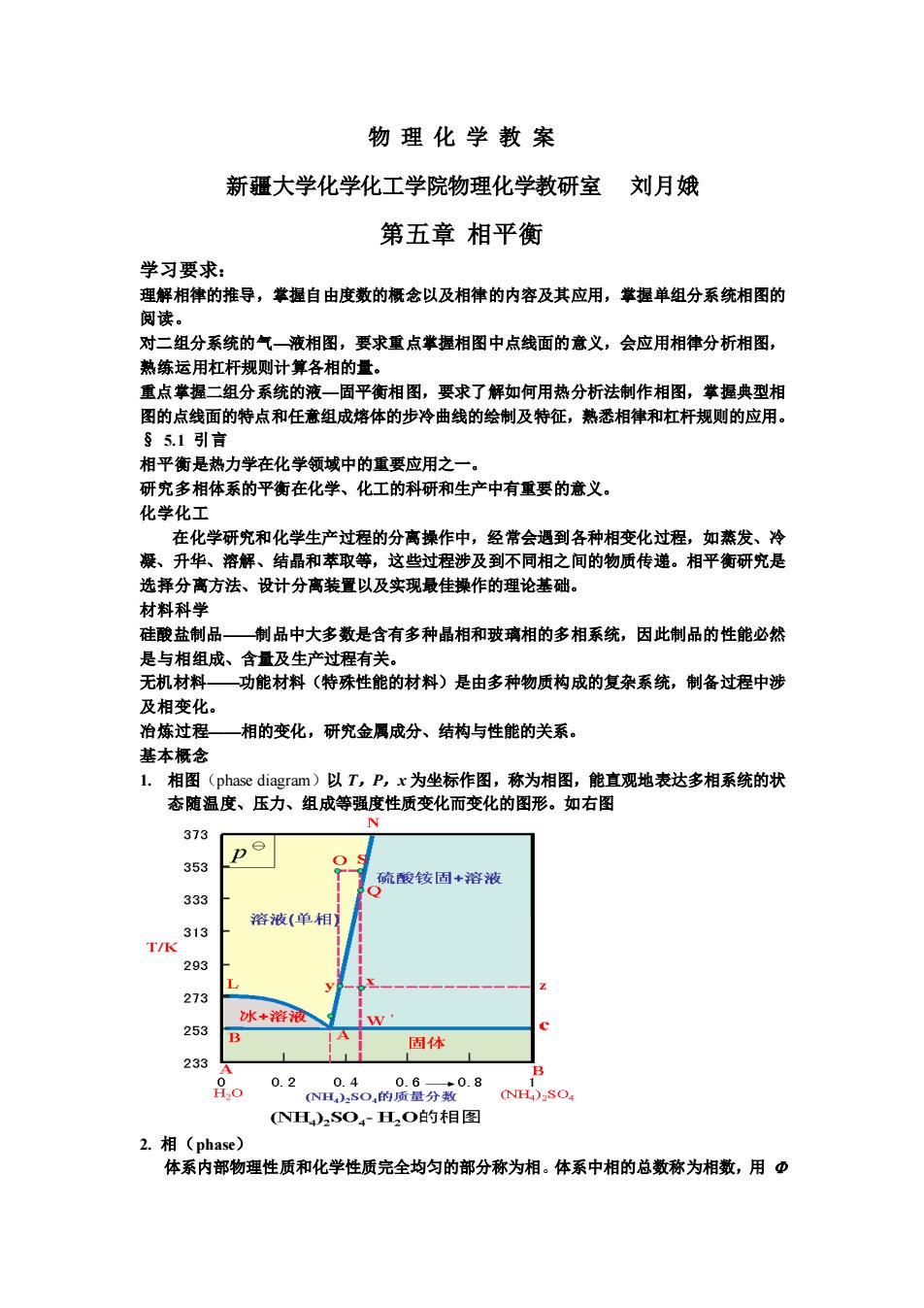
物理化学教案 新疆大学化学化工学院物理化学教研室刘月娥 第五章相平衡 学习要求: 理解相律的推导,举握自由度数的概念以及相律的内容及其应用,肇握单组分系统相图的 阅读。 对二组分系统的气一液相图,要求重点掌握相图中点线面的意义,会应用相律分析相图, 熟练运用杠杆规则计算各相的量。 重点掌握二组分系统的液一固平衡相图,要求了解如何用热分析法制作相图,掌握典型相 图的点梦的带点剂任意这培体的步冷曲线的绘制及特在,恭委相律鬼虹狂规则的应用。 相平衡是热力学在化学领域中的重婴应用之一。 研究多相体系的平衡在化学、化工的科研和生产中有重要的意义。 化学化工 在化学研究和化学生产过程的分高操作中,经常会通到各种相变化过程,如燕发、冷 凝、升华 溶解 过程涉及到不同相之 间的物质传递。相平衡研究是 选择分离方法、设计分高装置以及实现最佳操作的理论基础 材料科学 硅酸盐制品制品中大多数是含有多种晶相和玻璃相的多相系统,因此制品的性能必然 是与相组成、含量乃生产时程有关 无机材料 功能材料(特殊性能的材料)是由多种物质构成的复杂系统,制备过程中涉 及相变化。 治炼过程 —相的变化,研究金属成分、结构与性能的关系。 基本概念 L.相图(phase diagram)以T,P,x为坐标作图,称为相图,能直观地表达多相系统的状 态随温度、压力、组成等强度性质变化而变化的图形。如右图 373 353 硫酸铵固+溶液 333 313 溶液(单相】 T/k 293 273 253 冰+溶液 固体 233 o 0.2 NH)2SO4H,O的相图 2.相(phase) 体系内部物理性质和化学性质完全均匀的部分称为相。体系中相的总数称为相数,用币
物 理 化 学 教 案 新疆大学化学化工学院物理化学教研室 刘月娥 第五章 相平衡 学习要求: 理解相律的推导,掌握自由度数的概念以及相律的内容及其应用,掌握单组分系统相图的 阅读。 对二组分系统的气—液相图,要求重点掌握相图中点线面的意义,会应用相律分析相图, 熟练运用杠杆规则计算各相的量。 重点掌握二组分系统的液—固平衡相图,要求了解如何用热分析法制作相图,掌握典型相 图的点线面的特点和任意组成熔体的步冷曲线的绘制及特征,熟悉相律和杠杆规则的应用。 § 5.1 引言 相平衡是热力学在化学领域中的重要应用之一。 研究多相体系的平衡在化学、化工的科研和生产中有重要的意义。 化学化工 在化学研究和化学生产过程的分离操作中,经常会遇到各种相变化过程,如蒸发、冷 凝、升华、溶解、结晶和萃取等,这些过程涉及到不同相之间的物质传递。相平衡研究是 选择分离方法、设计分离装置以及实现最佳操作的理论基础。 材料科学 硅酸盐制品——制品中大多数是含有多种晶相和玻璃相的多相系统,因此制品的性能必然 是与相组成、含量及生产过程有关。 无机材料——功能材料(特殊性能的材料)是由多种物质构成的复杂系统,制备过程中涉 及相变化。 冶炼过程——相的变化,研究金属成分、结构与性能的关系。 基本概念 1. 相图(phase diagram)以 T,P,x 为坐标作图,称为相图,能直观地表达多相系统的状 态随温度、压力、组成等强度性质变化而变化的图形。如右图 2. 相(phase) 体系内部物理性质和化学性质完全均匀的部分称为相。体系中相的总数称为相数,用

表示。 相与相之间在指定条件下有明显的界面,在界面上宏观性质的改变是飞跃式的。 例如 冰两相平衡 冰与水之间有明显界面,越过这个截面,物理性质发生突变,冰与水 可以用物理方法分开 同一种物质的固体颗粒之间尽管有界面,但由于物理性质和化学性质完全相同,仍核一个相 对待。 3三种相态 :不论有多少种气 只有 相 液体:按其互溶程 可以组成一相、两相或三相共存。 固体:一般有一种固体便有一个相。两种固体粉末无论混合得多么均匀,仍是两个相(固体 溶液除外,它是单相)。 4相平衡:是指在一定条件下一个多相体系内各相 内的物质的种类和数量不随时间 变化的状岁 5,自由度 of freedom) 确定平衡体系的状态所必须的独立强度变量的数目称为自由度,用字母∫表示。这些强 度变量通常是压力、温度和浓度等。 这说明影响体系内相数的因素是强度性质而不是容量性质。例如水常温常压下是液体,与数 量无关若压力或温度改变则会引起相变。 如果已指定某个强度变量,除该变量以外的其它强度变量数称为条件自由度,用表示。 例如:指定了压力, 指定了压力和温度, 如水与水蒸气两相平衡:若指定了温度,水蒸气的压力使确定了:或者指定了水蒸气的压力, 温度便确定了,所以水与水蒸气两相平衡体系的自由度=1(温度或压): 若指定了水蒸气的压力或温度=0 §5.2多相系统平衡的一般条件 在一个封闭的多相体系中,相与相之间可以有热的交换、功的传递和物质的交流。对具有个 相体系的热力学平衡,实际上包含了如下四个平衡条件: (1)热平衡条件:设体系有α,B,.,F个相,达到平衡时,各相具有相同温度 Ta=TB=.=Th (2)压力平衡条件:达到平衡时各相的压力相等 D=p=.=p (3)相平衡条件:任一物质B在各相中的化学势相等,相变达到平衡 哈=唱==唱 (4)化学平衡条件:化学变化达到平衡 4B=0 B §5.3相律 l、相律(phase rule):
表示。 相与相之间在指定条件下有明显的界面,在界面上宏观性质的改变是飞跃式的。 例如水—冰两相平衡,冰与水之间有明显界面,越过这个截面,物理性质发生突变,冰与水 可以用物理方法分开。 同一种物质的固体颗粒之间尽管有界面,但由于物理性质和化学性质完全相同,仍按一个相 对待。 3.三种相态 气体:不论有多少种气体混合,只有一个气相。 液体:按其互溶程度可以组成一相、两相或三相共存。 固体:一般有一种固体便有一个相。两种固体粉末无论混合得多么均匀,仍是两个相(固体 溶液除外,它是单相)。 4.相平衡:是指在一定条件下一个多相体系内各相 内的物质的种类和数量不随时间 变化的状态 5.自由度(degrees of freedom) 确定平衡体系的状态所必须的独立强度变量的数目称为自由度,用字母 f 表示。这些强 度变量通常是压力、温度和浓度等。 这说明影响体系内相数的因素是强度性质而不是容量性质。例如水常温常压下是液体,与数 量无关,若压力或温度改变则会引起相变。 如果已指定某个强度变量,除该变量以外的其它强度变量数称为条件自由度,用 表示。 例如:指定了压力, 指定了压力和温度, 如水与水蒸气两相平衡:若指定了温度,水蒸气的压力便确定了;或者指定了水蒸气的压力, 温度便确定了,所以水与水蒸气两相平衡体系的自由度 f* =1(温度或压力); 若指定了水蒸气的压力或温度,f*=0 § 5.2 多相系统平衡的一般条件 在一个封闭的多相体系中,相与相之间可以有热的交换、功的传递和物质的交流。对具有 个 相体系的热力学平衡,实际上包含了如下四个平衡条件: (1)热平衡条件:设体系有 个相,达到平衡时,各相具有相同温度 (2)压力平衡条件:达到平衡时各相的压力相等 (3) 相平衡条件: 任一物质 B 在各相中的化学势相等,相变达到平衡 (4) 化学平衡条件:化学变化达到平衡 § 5.3 相律 1、相律(phase rule): , , ,F T T T = = = F p p p = = = F B B B = = = F B B B = 0

是表述平衡体系中相数、独立组分 、自由度数和影响物质性质的外界因素(如温度、压力 电场、磁场、重力场等)之间关系的规律 2.相律的推导 依据:自由度数=总变量数一方程式数 个多相多组分系统中,有S种物质1、2、3.S)分布在中个相(a、B、y.)中。 对于 相 必须知 、x口才能确定其状态 。所以 决定。相状态的变量共有(S+2)个。系统中共有中个相,则整个系统的变量数为 Φ(S+2) 但这些变量不是完全独立的,相互之间有联系 f=中(S+2)平衡时变量间的关系式数 (1)系统处于热力学平衡态,有 热平衡 Ta= (中1) 个等式 力平衡pa=.=p中 (中-1)个等式 相平衡4a1=.=4中1S(中-1)个等式 as=.=中 (2)每个相中有S种物质,2xB=1 xS =/-x1-x2-xs-1 中个浓度关系式。 (3)独立化学平衡数为R,独立浓度关系数为R'。 fS+2)-(-l)-(中-)-1)-中-R-R =S-R-R-Φ+2=C-+2 f=S-R-R-+2 相律是相平衡体系中揭示相数D,独立组分数C和自由度了之间关系的规律。式中2通常 指T,p两个变量。相律最早由Gibbs提出,所以又称为Gibbs相律。如果除T,p外,还受 其它力场影响,则2改用n表示,即: f+F=C+n 例如:盐溶液与纯溶剂达渗透平衡, Φ=2,S=2,=3温度和压力(渗透平衡时有两个压) R=0,R'-=0,C=2 f=C+3=2-2+3=3 3.物种数和独立组分数 (1)物种数 number of substance 一系统中所包含的可以单独分离出来、并能独立存在的化学物质的数目,称为系统的物 种敷”,记作S 如:NaC的水溶液中 Na 和OH.但只能算两种物质,S=2 处于不同相态的同种化学物质,只能算一个物种。如:液态水和水蒸气。 (2)独立组分数 (number ofindependent component
是表述平衡体系中相数、独立组分、自由度数和影响物质性质的外界因素(如温度、压力、 电场、磁场、重力场等)之间关系的规律。 2.相律的推导 依据:自由度数=总变量数-方程式数 设一个多相多组分系统中,有 S 种物质 1、2、3.S)分布在φ个相(α、β、γ.φ)中。 对于其中任意一相α相,必须知道 Tα、pα、xα1、.、xαs,才能确定其状态。所以, 决定α相状态的变量共有(S + 2)个。系统中共有φ个相,则整个系统的变量数为 Φ(S + 2) 但这些变量不是完全独立的,相互之间有联系 f = φ (S + 2)-平衡时变量间的关系式数 (1)系统处于热力学平衡态,有 热平衡 Tα= . = T φ (φ -1) 个等式 力平衡 pα = . = p φ (φ -1) 个等式 相平衡 μα1 = . = μφ 1 S(φ -1) 个等式 ┊ ┊ μαs = . = μφ s (2)每个相中有 S 种物质,ΣxB = 1, xS =1- x1 – x2-xs-1 φ个浓度关系式。 (3)独立化学平衡数为 R,独立浓度关系数为 R'。 f = φ(S + 2) –(φ–1) –(φ–1) –S(φ–1)- φ – R –R' = S – R – R` –φ+ 2 = C –φ + 2 f = S – R – R` –φ+ 2 = C –φ + 2 相律是相平衡体系中揭示相数 ,独立组分数 C 和自由度 f 之间关系的规律。式中 2 通常 指 T,p 两个变量。相律最早由 Gibbs 提出,所以又称为 Gibbs 相律。如果除 T,p 外,还受 其它力场影响,则 2 改用 n 表示,即: 例如:盐溶液与纯溶剂达渗透平衡, =2,S=2,n=3 温度和压力(渗透平衡时有两个压力) R=0,R’=0,C=2 f =C- +3=2-2+3=3 3.物种数和独立组分数 (1)物种数 ( number of substance ) ——系统中所包含的可以单独分离出来、并能独立存在的化学物质的数目,称为系统的“物 种数”,记作 S。 如:NaCl 的水溶液中,有 Na+、Cl-、H+和 OH- 但只能算两种物质,S = 2。 处于不同相态的同种化学物质,只能算一个物种。如:液态水和水蒸气。 (2)独立组分数 (number of independent component ) f C n + = + F

一足以确定平衡体系中的所有各相组成所需要的最少的物质的数目,记作C. S≥C C-S-R-R R是独立化学平衡数, R是独立浓度关系数。 (A)对于独立化学平衡数,要注意独立”两个字。 例如:系统中含有C(s以、C0(g、H20(g、C02(g、H2(g等五种物质,可能存 在的反应有 (1)C(s)+H20(g)=C0(g)+H2(g) (2)C(s)+C02(g)=2C0(g) 个反应 开 不是独立的,反应(3)可以由()和(2)得到,所以真正独立的平 衡数只有R=2. (B)对于浓度关数R”,要注意应限于在同一相中应用。假如分解产物(反应产物)分别 处于不同相中,则不能计算浓度关系数。 例如:CCO3(s) Cao (s)+co2 (g 这个分解反应,产物是固相,C02是气相,所以虽然两者的量之比是1:1, 因而,无浓度限制关系,所以 R=0,S=3,R=1.C=2。 例题 ()、冰水共存 C-1,D=2(冰、水),f=1-2+2=1(T或p) (2、NH4CI(S部分分解为NH3g和HC1(g S-3,R1,R=l,Φ2(NH4C固相、气相) f=3-1-1-2+2=1 (TP、xNH3或xHCI其中之一) (3)1000K下,NH3、H2、N2三气平衡 S=3,R=1(2NH3=3H2+N2),D=1 f=CD+1=2(p、xNH3、xH2或xN2其中之二) 4.相律的几点说明 一般情况下,只考虑温度T和压力p这两个因素时,式中的广2,于是相律为 f=C-Φ+2 若指定了温度或压力则 f*=CΦ+1 ∫*一条件自由度 若温度和压力同时固定,则 f齿*=CΦ
——足以确定平衡体系中的所有各相组成所需要的最少的物质的数目,记作 C。 S≥C C = S – R – R` R 是独立化学平衡数, R'是独立浓度关系数。 (A)对于独立化学平衡数,要注意“独立” 两个字。 例如:系统中含有 C(s)、CO(g)、H2O(g)、CO2(g)、H2(g)等五种物质,可能存 在的反应有 (1) C(s)+H2O(g)=CO(g)+H2(g) (2) C(s)+CO2(g)=2CO(g) (3)CO(g)+H2O(g)=CO2(g)+ H2(g) 但这三个反应并不是独立的,反应(3)可以由(1)和(2)得到,所以真正独立的平 衡数只有 R=2。 (B)对于浓度关数 R’,要注意应限于在同一相中应用。假如分解产物(反应产物)分别 处于不同相中,则不能计算浓度关系数。 例如:CaCO3(s)=CaO(s)+CO2(g) 这个分解反应,产物是固相,CO2 是气相,所以虽然两者的量之比是 1:1, 但 , , 因而,无浓度限制关系, 所以 R’=0,S=3,R=1, C=2。 例题 (1)、冰水共存 C=1, =2 (冰、水), f = 1-2+2=1 (T 或 p) (2)、NH4Cl(s)部分分解为 NH3(g)和 HCl(g) S=3,R=1,R’=1, =2 (NH4Cl 固相、气相) f = 3 – 1 – 1 – 2 + 2 = 1 (T、p、 x NH3 或 xHCl 其中之一) (3) 1000K 下,NH3、H2、N2 三气平衡 S=3,R=1 (2NH3=3H2+N2), =1 f = C- +1=2 (p、xNH3、x H2 或 x N2 其中之二) 4. 相律的几点说明 一般情况下,只考虑温度 T 和压力 p 这两个因素时,式中的 n=2,于是相律为 f =C- +2 若指定了温度或压力,则 f * =C- +1 f *—条件自由度; 若温度和压力同时固定,则 f ** = C-

5.相律的意义 多组分多相系统是十分复杂的,但借助相律可以确定研究的方向。相律表明了相平衡系统 中有几个独立变量,当独立变量选定了之后,相律还表明其他的变量必为这几个独立变量 的函数(但是相律不能告诉我们这些函数的具体形式)。 §5.4单组分体系的相平衡 单组分体系的相数与自由度 C=1,F=C-Φ+2=3-Φ (1)D1时,单相,双变量系统(T、p) (2)D=2时,两相共存,F=1,单变量系统 (T)—克克方程 (3)D-3时,三相共存,F=0,无变量系统 表示某个相状态(如相态、组成、温度等)的点称为相点。 物系点: 相图中表示体系总状态的点称为物系点。在下x图上,物系点可以沿着与温度坐标平 行的垂线上 下移动:在水盐体系图上,随着含水量的变化,物系点可沿着与组成坐标平 移 在单相区,物系点与相点重合:在两相区中,只有物系点,它对应的两个相的组成由对应 的相点表示。 一、单组分体系两相平衡一克拉贝龙方程 若原来在一定条件下建立了两相平衡,如果温度改变T,则燕气压必改变P,在新的条件下 建立新的平衡可表示为 1.克拉佩龙方程 B(a)K¥D→B(B) dG (a)=dG (B) dG(a) dG(B) dG.(a)=-S.(a)dT+V_(a)dp B(a←¥+中→B(B)dG.()=-S.(BaT+K.B dT-△y △2S。=A2Hn/T dT_T△y dp△gSn dp△2H 即克拉佩龙(Clapeyron BP E)方程 2.固液平衡,固固平衡积分式 3液气、固气平衡的蒸气压方程一克劳修斯-克拉佩龙方程 dT TAV
5. 相律的意义 多组分多相系统是十分复杂的,但借助相律可以确定研究的方向。相律表明了相平衡系统 中有几个独立变量,当独立变量选定了之后,相律还表明其他的变量必为这几个独立变量 的函数(但是相律不能告诉我们这些函数的具体形式)。 § 5.4 单组分体系的相平衡 单组分体系的相数与自由度 C = 1,F = C - + 2 = 3 – (1)=1 时,单相,双变量系统(T、p) (2)=2 时,两相共存,F=1,单变量系统 p=f(T)——克-克方程 (3)=3 时,三相共存,F=0,无变量系统 max=3, f max=2,双变量体系的相图可用平面图表示。 相点 : 表示某个相状态(如相态、组成、温度等)的点称为相点。 物系点 : 相图中表示体系总状态的点称为物系点。在 T-x 图上,物系点可以沿着与温度坐标平 行的垂线上、下移动;在水盐体系图上,随着含水量的变化,物系点可沿着与组成坐标平 行的直线左右移动。 在单相区,物系点与相点重合;在两相区中,只有物系点,它对应的两个相的组成由对应 的相点表示。 一、单组分体系两相平衡—克拉贝龙方程 若原来在一定条件下建立了两相平衡,如果温度改变 dT,则蒸气压必改变 dP,在新的条件下 建立新的平衡,可表示为 1. 克拉佩龙方程 即克拉佩龙(Clapeyron B P E)方程 2.固-液平衡,固-固平衡积分式 3.液-气、固-气平衡的蒸气压方程——克劳修斯-克拉佩龙方程 , B( ) B( ) T p ⎯⎯⎯→ 平衡 B( ) B( ) T T p p ⎯⎯⎯⎯⎯→ 平衡 + d , + d d ( ) Gm d ( ) Gm d ( ) d ( ) G G m m = d ( ) ( )d ( )d G S T V p m m m = − + d ( ) ( )d ( )d G S T V p m m m = − + = m m d d T V p S S H T m m = / = m m d d T T V p H = 1 fus m 2 fus m ln d T V p T H = fus m 1 fus m V T T p H = vap m vap m d d p H T T V

若m(g)>>m(),近似有△vapm≈m(g)将m(g-RTp代入上式得 出品 dlnp_△.apH dT RT 此即克劳修斯-克拉佩龙方程的微分式。克劳修斯-克拉佩龙方程定积分式 nh.-△H(1.1) P RT T 克一克方程的不定积分式 In p=-bHeC RT 对某液体若有一系列不同温度下饱和蒸气压的数据,做即-1T图,可得一直线,由此直线 的斜率和截矩即可求得液体的△vapHm及式中的C。 4.液体的燕发:与温度的关系 如果精确计算】 则需考虑△vapHm与温度的关系。 d(△anH) dT ≈△Cm(T) 5.Trouton规则(Trouton's Rule) 关于摩尔蒸发焙,Trouton根据大量的实验事实,总结出一个近似规则。 即对于多数非极性液体,在正常沸点b时燕发,熵变近似为常数,摩尔蒸发培变与正常沸 点之间有如下近似的定量关系: △=He8J-k1.mor 这就称为Trouton's Rule。对极性液体、有缔合现象的液体以及b小于150K的液体,该 规则不适用 二、外压对液(或固)体饱和蒸气压的影响 如果液体放在惰性气体(空气)中,并设空气不溶于液体,这时液体的燕气压将随着外压的 改变而作相应的改变,通常是外压增大,液体的蒸气压也升高 dp(g)。V四 dp①)V(g) 式中,p*(g和p心分别为液体的饱和蒸气压和液休所受的外压 假设气相为理想气体,则有如下的近似关系: -
若 Vm(g)>>Vm(l),近似有 ΔvapVm≈Vm(g) 将 Vm(g)=RT/p 代入上式得: 此即克劳修斯-克拉佩龙方程的微分式。克劳修斯-克拉佩龙方程定积分式: 克—克方程的不定积分式 对某液体若有一系列不同温度下饱和蒸气压的数据,做 lnp-1/T 图,可得一直线,由此直线 的斜率和截矩即可求得液体的ΔvapHm 及式中的 C。 4.液体的蒸发焓与温度的关系 如果精确计算,则需考虑ΔvapHm*与温度的关系。 5.Trouton 规则(Trouton’s Rule) 关于摩尔蒸发焓,Trouton 根据大量的实验事实,总结出一个近似规则。 即对于多数非极性液体,在正常沸点 Tb 时蒸发,熵变近似为常数,摩尔蒸发焓变与正常沸 点之间有如下近似的定量关系: 这就称为 Trouton’s Rule 。对极性液体、有缔合现象的液体以及 Tb 小于 150 K 的液体,该 规则不适用。 二、外压对液(或固)体饱和蒸气压的影响 如果液体放在惰性气体(空气)中,并设空气不溶于液体,这时液体的蒸气压将随着外压的 改变而作相应的改变,通常是外压增大,液体的蒸气压也升高 式中,p*(g)和 p(l)分别为液体的饱和蒸气压和液体所受的外压。 假设气相为理想气体,则有如下的近似关系: = vap m 2 d d / p H T RT p = vap m 2 dln d p H T RT = − − 2 vap m 1 2 1 1 1 ln p H p R T T = − + vap m ln H p C RT = * * m * m d (g) (l) d (l) (g) p V p V vap m -1 1 b 88 J K mol H T − * vap m β α ,m d( ) ( ) d p H C T T g m * * e g g (1) ln ( ) p V p p p RT = −

三、水的相图 1.20的相平衡实验数据 水的和和然 气 平换玉力MP 611.0 611.0×100 611.0 2.水的相图 水的相图是根据以上实验数据绘制 三个单相区:在汽、液、固三个单相区内,P=1,F=2温度和压力独立地有限度地变化不会引 起相的 三条两相平衡线:P-2,F1压力与温度只能改变一个指定了压力,则温度由体系自定 OA是气-液两相平衡线,即水的蒸气压曲线。它不能任意延长,终止于临界点。临界点 T=647K,D=2.2×107Pa这时气-液界面消失。 高于临界温度,EAF区为超临界流体区,气相区,不能用加压的方法使气体液化! 0B是气-固两相平衡线,即冰的升华曲线,理论上可延长至0K附近 是液固两相平衡线,当C点延长至压力大于210时,相图变得复杂,有不同结构的 冰生成。 OD是A0的延长线,是过冷水和水蒸气的介稳平衡线。因为在相同温度下,过冷水的蒸 气压大于冰的蒸气压,所以OD线在OB线之上。过冷水处于不稳定状态,一旦有凝豪中 心出现,就立即全部变成冰。 0点 是三相点(trip pont),气-液-固三相共存,P-3F-0,三相点的温度和压力皆由体 系自定。 H20的三相点温度为273.16K,压力为610.62Pa。 三相点与冰点不同: 三相点:是物质自身的特性,不能加以改变。是纯水在其饱和蒸气压下凝固点,单组分系 冰点:p101.325kP下,被空气饱和的水的嫌固点(27315K)。由于有空气溶入,是多组 份系统。改变外压,冰点也随之改变
三、水的相图 1.H2O 的相平衡实验数据 2.水的相图 水的相图是根据以上实验数据绘制 三个单相区:在汽、液、固三个单相区内,P=1,F=2 温度和压力独立地有限度地变化不会引 起相的改变。 三条两相平衡线: P=2,F=1 压力与温度只能改变一个指定了压力,则温度由体系自定。 OA 是气-液两相平衡线,即水的蒸气压曲线。它不能任意延长,终止于临界点。临界点 这时气-液界面消失。 高于临界温度, EAF 区为超临界流体区,气相区,不能用加压的方法使气体液化。 OB 是气-固两相平衡线,即冰的升华曲线,理论上可延长至 0 K 附近。 OC 是液-固两相平衡线,当 C 点延长至压力大于 2108时,相图变得复杂,有不同结构的 冰生成。 OD 是 AO 的延长线,是过冷水和水蒸气的介稳平衡线。因为在相同温度下,过冷水的蒸 气压大于冰的蒸气压,所以 OD 线在 OB 线之上。过冷水处于不稳定状态,一旦有凝聚中 心出现,就立即全部变成冰。 O 点 是三相点(triple point),气-液-固三相共存,P=3,F=0。三相点的温度和压力皆由体 系自定。 H2O 的三相点温度为 273.16 K,压力为 610.62 Pa。 三相点与冰点不同: 三相点:是物质自身的特性,不能加以改变。是纯水在其饱和蒸气压下凝固点,单组分系 统。 冰 点:p=101.325kPa 下,被空气饱和的水的凝固点(273.15K)。由于有空气溶入,是多组 份系统。改变外压,冰点也随之改变。 T = 647 K , 7 p = 2.2 10 Pa

0。+空气 np( Hp( 冰点温度比三相点温度低是由两种因素造成的:(1)因水中溶有空气,使凝固点下降 0.0023℃;(2)因外压从611.0P增加到101.325ka,使凝固点下降0.0075℃。两种结果 使冰点比三相点低0.0098℃。 酒相丙相苹垫的整津约可由Chusius-Chapcy1on方程或Cpg1on方密求得。 OA线 斜率为正 A0 OB线 斜率为正。 dlnp_△wHm dr RT2 △hHm>0 OC线斜率为负。 dp_△sH dT TAV △eH>0,△y<0 四、超临界状态 超临界流体((supercritical fuid)是指温度及压力均处于临界点以上的流体 如:CO2的相图 在临界点C以上就是超临界流体区。它基本上仍是一种气态,但又不同于一般气体,是一 种稠密的气态。 个数量级。 3、扩散速度比液体快,扩散系数比流体大两个数量级 故:有较好的流动性和传递性能(例如热传导等) 物质在超临界流体中的落解度,受压力和温度的影响很大,可以利用升温,降压手段或两 者兼用将超临界流体中所溶解的物质分离出来,达到分离提纯的目的(它兼有精馏和萃取两 种作用)
冰点温度比三相点温度低是由两种因素造成的:(1)因水中溶有空气,使凝固点下降 0.0023℃;(2)因外压从 611.0Pa 增加到 101.325 kPa,使凝固点下降 0.0075℃ 。两种结果 使冰点比三相点低 0.0098℃。 两相平衡线的斜率: 三条两相平衡线的斜率均可由 Clausius-Clapeyron 方程或 Clapeyron 方程求得。 OA 线 斜率为正 OB 线 斜率为正。 OC 线 斜率为负。 四、超临界状态 超临界流体(supercritical fluid)是指温度及压力均处于临界点以上的流体。 如:CO2 的相图 在临界点 C 以上就是超临界流体区。它基本上仍是一种气态,但又不同于一般气体,是一 种稠密的气态。 1、密度比一般气体要大两个数量级,与液体相近 2、黏度比液体小 ,黏度系数一般比液体小一个数量级。 3、扩散速度比液体快,扩散系数比流体大两个数量级 故:有较好的流动性和传递性能(例如热传导等) 物质在超临界流体中的溶解度,受压力和温度的影响很大,可以利用升温,降压手段(或两 者兼用)将超临界流体中所溶解的物质分离出来,达到分离提纯的目的(它兼有精馏和萃取两 种作用)。 vap m 2 d ln d p H T RT = vap m H 0 m 2 d ln d p subH T RT = sub m H 0 fus m fus d d p H T T V = fus fus H V 0, 0

招临界流体荟取 超临界流体的实际应用 超临界流体色谱 超临界流体中的化学反应 超临界流体萃取(从天然物「用超临界C02从如啡豆中除去咖啡因 中抽取有效成分 从烟草中脱 尼古 从大豆或玉米胚芽中分离油脂 对花生油棕榈油大豆油脱臭 从红花中提取红花甙(苷)及红花醌甙 (治疗高血压和肝病的有效成分) 缺点:涉及高压系统大规模使用时,其工艺过程和技术的要求高设备费用也大 §5.5二组分系统的相图及其应用 p-r图和Tx图 一组分 f=C-b+2=4-D mmx=3,(T,p,x)一立体图:保持一个变量为常量,从立体图上得到 平面截面图 (1)保持温度不变,得pP-x图较常用 (2)保特压力不变,得Tx图常用 (3)保持组成不变,得TD图不常用 Dma=4,∫min=0,无变量系统,最多四相共存,此时T、p、x为定值不能政变 一、二组分气液平衡体系 (一)、理想的二组分液态混合物:完全互溶双液系 定义:两个纯液体可按任意比例互溶形成理想的液体混合物,每个组分都服从拉乌尔定律。 如苯和甲苯正已烷与正庚烧等可形成这种双液系 1.压力组成图 (1)液相线(pxA)的绘制 PA=PAXA P=P+Pu =0,p=Pi Pu=Pixa =(-Ps)+Pe x=1,p=p 等温Px图 p-Px+Pa XA
超临界流体萃取 超临界流体的实际应用 超临界流体色谱 超临界流体中的化学反应 超临界流体萃取 (从天然物 用超临界 CO2 从咖啡豆中除去咖啡因 中抽取有效成分) 从烟草中脱除尼古丁 从大豆或玉米胚芽中分离油脂 对花生油/棕榈油/大豆油脱臭 从红花中提取红花甙(苷)及红花醌甙 (治疗高血压和肝病的有效成分) 缺点:涉及高压系统,大规模使用时,其工艺过程和技术的要求高,设备费用也大。 § 5.5 二组分系统的相图及其应用 p-x 图 和 T-x 图 二组分 f = C – + 2 = 4 – min= 1, f max= 3,(T,p , x)——立体图;保持一个变量为常量,从立体图上得到 平面截面图 (1)保持温度不变,得 p-x 图 较常用 (2)保持压力不变,得 T-x 图 常用 (3)保持组成不变,得 T-p 图 不常用。 max= 4, f min= 0,无变量系统,最多四相共存,此时 T、p、x 为定值不能改变 一、二组分气-液平衡体系 (一)、理想的二组分液态混合物:完全互溶双液系 定义: 两个纯液体可按任意比例互溶形成理想的液体混合物,每个组分都服从拉乌尔定律。 如苯和甲苯;正己烷与正庚烷等可形成这种双液系。 1. 压力-组成图 (1)液相线(p-xA)的绘制 A A A B B B p p x p p x = = A B * A B A B ( ) p p p p p x p = + = − + A B A A 0 1 , , x p p x p p = = = =

(2气相线(p)的绘制 YA=PA a=1- D P=PA+Pa=Px+puxa Px+pa(1-xa)pa+(pk -pa)xa 各+巴- 等温p-y图 p-P+P 液相线 g-l PA x XA- A( (3)相图分析 ①在液相线之上,体系压力高于任一混合物的饱和蒸气压,气相无法存在,是液相区。 ②在气相线之下,体系压力低于任一混合物的饱和蒸气压,液相无法存在,是气相区。 这两个区为双变量系统,T 定时,F=21+1=之,有两个自由度,压力、组成可发生改变 ®在液相线和气相线之间的梭形区内,是气液两相平衡,为单变量系统, F=2-2+1=1 只有一个自由度,p和y为x的函数。 0点:当压力为p时,液相组成为xG,气相组成为xL。 G、L点分别表示气、液两相中B的组成一相点。两相点的连线称为结线(tie line)。 0点表示整个系统中B的组成一系统点 2.温度组成图(沸点-组成下x) (1)沸点一溶液的蒸气压等于外压时,溶液开始沸腾,此时温度称为该溶液的沸点。 一般,燕气压越高的溶液(易挥发),其沸点越低。反之蒸气越低的溶液,其沸点越高 pAT。Tx图在讨论蒸馏时十分有用,因为 蒸馏通常在等压下进行 (2)温度一组成图(沸点一组成Tx) 若已知两个纯液体在不同温度下蒸气压的数据,可通过计算得出温度一组成图。 人==1-= P(1-x8) D D +(pa-pA)x L2为液体开始沸腾的温度,开始有气泡出现,相应的温度成为溶液的泡点(bubble point)。 液相线—泡点线
(2)气相线(p-y)的绘制 (3)相图分析 ①在液相线之上,体系压力高于任一混合物的饱和蒸气压,气相无法存在,是液相区。 ②在气相线之下,体系压力低于任一混合物的饱和蒸气压,液相无法存在,是气相区。 这两个区为双变量系统,T 一定时,F = 2-1+1=2,有两个自由度,压力、组成可发生改变。 ③在液相线和气相线之间的梭形区内,是气-液两相平衡,为单变量系统,F = 2-2+1 = 1, 只有一个自由度,p 和 y 为 x 的函数。 O 点:当压力为 p 时,液相组成为 xG,气相组成为 xL。 G、L 点分别表示气、液两相中 B 的组成——相点。两相点的连线称为结线(tie line)。 O 点表示整个系统中 B 的组成——系统点 2.温度—组成图(沸点—组成 T-x) (1)沸点——溶液的蒸气压等于外压时,溶液开始沸腾,此时温度称为该溶液的沸点。 一般,蒸气压越高的溶液(易挥发),其沸点越低。反之蒸气越低的溶液,其沸点越高。 若 A B p p ,在一定 p 下, T T A B T-x 图在讨论蒸馏时十分有用,因为 蒸馏通常在等压下进行。 (2)温度—组成图(沸点—组成 T-x) 若已知两个纯液体在不同温度下蒸气压的数据,可通过计算得出温度-组成图。 L2 为液体开始沸腾的温度,开始有气泡出现,相应的温度成为溶液的泡点(bubble point)。 液相线——泡点线。 A A p y p = B A y y = −1 * * A B A B B A p p p p x p x = + = + * * A A B (1 ) A = + − p x p x * * * B A B A = + − p p p x ( ) * * * * ( ) A A A A A A B A P P x y P P P P x = = + − A A A B A B A B A B A B (1 ) (1 ) 1 ( ) p x p x p x y y p p p p p x − − = = − = + −