新疆大学：《物理化学》课程授课教案（讲义）第六章 化学平衡

物理化学教案 新疆大学化学化工学院物理化学教研室刘月娥 第六章化学平衡 教学目的：本章应用热力学原理来研究化学反应进行的限度，要求学生掌握平衡常数的计 算，并根据热力学原理，判断压力、温度、情性气体等因素对平衡移动的影响，为实际生 产提供依据， 学习要求： 重点掌握化学反应等温方程。 掌握各种反应体系标准平衡常数和其他平衡常数的表达式及相互间变换。 里点誉握温度对平衡常数的影响一Van'tHoff方程的定积分式、不定积式 压力 反应平衡移动的影响和 成变化的计算。 了解同时平衡计算原则及方法。 引言 化学平衡的定义、特点及分类： 1化学平衡的动力学定义：化学平衡是指在一定条件下，化学反应的正向反应速率与逆向反 应速度相等，反应体系中宏观性质不随时间变化的状态。 2.化学平衡的特点：达到平衡时正逆反应的速率相同，体系中各物质的量均不随时间而改 变，当外界条件改变时，平衡状态就可能发生改变，所以化学平衡是一种动态平衡。 3.化学平衡反应分类 为了过论问颗方便，把化学平衡反应分为两大举！ ()均相化学平衡 指平衡体系中各物质处于同一相。 均相化学平衡体系又可分为气相反应平衡和液相反应平衡两类 如N2(g+3H2(g)=2NH3(g)都处于气相 (2)复相化学反应指平衡体系中各物质以不同相态存在 CaC03(s)=CaO(s)+C02(g) 化工生产或化学研究中的问题： A B- 一定条件：→ T、p、c 何时平衡（限度）？ 改变外界因素如：温度、压力、浓度平衡如何 研究方法：热力学基本原理、方法 反应： 0=∑yB 一自发 △，Gm≤0 (dp=-0、dT=0、=0) ~平衡

1 物 理 化 学 教 案 新疆大学化学化工学院物理化学教研室 刘月娥 第六章 化学平衡 教学目的： 本章应用热力学原理来研究化学反应进行的限度，要求学生掌握平衡常数的计 算，并根据热力学原理，判断压力、温度、惰性气体等因素对平衡移动的影响，为实际生 产提供依据。 学习要求： 重点掌握化学反应等温方程。 掌握各种反应体系标准平衡常数和其他平衡常数的表达式及相互间变换。 重点掌握温度对平衡常数的影响－Van't Hoff 方程的定积分式、不定积式。 压力、惰性气体对气相反应平衡移动的影响和组成变化的计算。 了解同时平衡计算原则及方法。 引 言 化学平衡的定义、特点及分类： 1.化学平衡的动力学定义：化学平衡是指在一定条件下，化学反应的正向反应速率与逆向反 应速度相等，反应体系中宏观性质不随时间变化的状态。 2. 化学平衡的特点：达到平衡时正逆反应的速率相同，体系中各物质的量均不随时间而改 变，当外界条件改变时，平衡状态就可能发生改变，所以化学平衡是一种动态平衡。 3. 化学平衡反应分类: 为了讨论问题方便，把化学平衡反应分为两大类： (1) 均相化学平衡 指平衡体系中各物质处于同一相。 均相化学平衡体系又可分为气相反应平衡和 液相反应平衡两类 如 N2(g)+3H2(g ) =2NH3(g ) 都处于气相 (2) 复相化学反应 指平衡体系中各物质以不同相态存在 如 CaCO3(s)=CaO(s)+CO2(g) 化工生产或化学研究中的问题： 何时平衡（限度）? 改变外界因素如：温度、压力、浓度平衡如何? 研究方法：热力学基本原理、方法 反应： 自发 r m G ≤0 (dp=0、dT=0、W'=0) 平衡 0 B B B = 

§6.1化学平衡的条件和反应的亲和势 一、化学反应的平衡条件和反应进度的关系 为了探讨化学平衡的条件，从化学热力学角度看化学平衡。 考察一个封闭的单相体系，不作非膨张功，发生了一个化学反应，设为： dD+eE+.→F+gG+ 即各物质的变化量必须满足： 0=2B 根据反应进度的定义，可以得到： ds、a d。=yd5 VB 根据热力学基本方程 dG=-S7++4，dn, 等温、等压条件下， (dGp=hadh=∑n4hd5 (dna=vads) ,-4 (a) 当5-1mol时 (a,G.n=∑4 (b) 密4回 (A,G.=∑hO 这两个公式适用条件： (1)等温、等压、不作非膨胀功的一个化学反应： (2)反应过程中，各物质的化学势保持不变。即反应过程中各物质的浓度不变。 所以公式(a)表示有限体系中发生微小的变化： 公式(b)表示在大量的体系中发生了反应进度等于1ml的变化，这时各物质的浓度基本不 变，化学势才保持不变。 用以上两式，可以判断化学反应的方向和限度 用 定p,∑4或(aChp 判断都是等效的。 (A.G).0 等温等压下反应自发地向左进行，不可能自发向右进行 (△，Gm)rp=0 反应等温等压下达到平衡

2 §6.1 化学平衡的条件和反应的亲和势 一、化学反应的平衡条件和反应进度的关系 为了探讨化学平衡的条件，从化学热力学角度看化学平衡。 考察一个封闭的单相体系，不作非膨胀功，发生了一个化学反应，设为： 即各物质的变化量必须满足： 根据反应进度的定义，可以得到： 根据热力学基本方程 等温、等压条件下， 当 时 这两个公式适用条件： （1）等温、等压、不作非膨胀功的一个化学反应； （2）反应过程中，各物质的化学势 保持不变。即反应过程中各物质的浓度不变。 所以公式（a)表示有限体系中发生微小的变化； 公式(b)表示在大量的体系中发生了反应进度等于 1 mol 的变化，这时各物质的浓度基本不 变，化学势才保持不变。 用以上两式，可以判断化学反应的方向和限度 用 判断都是等效的。 等温等压下反应自发地向右进行 等温等压下反应自发地向左进行，不可能自发向右进行 反应等温等压下达到平衡 d e f g D E F G + +  → + +  B B 0 B = B B d d n   = d d nB B =  B B B d d d d G S T V p n = − + + , B B B B B B （ ）d d d G n T p = =       B B (d d ) n =  , B B B ( ) (a) T p G     =    = 1 mol r m , B B B (b) （ ）  = G T p   , B B B ( ) (a) T p G     =   r m , B B B (b) （ ）  = G T p   , B r m , B ( ) , ( ) T p B T p G   G      或 r m , ( )  G T p  0 r m , ( ) 0  G T p  r m , ( ) 0  G T p =

0-1mol之间。 爱，0 反应自发向左进行，趋向平衡 ，0 反应达到平衡 由此可见：化学反应平衡的本质 从动力学看是正逆反应速率相等 从热力学看，当各个反应物的化学势与其计量系数乘积之和等于各个产物的化学势与其计量 系数乘积之和时反应达平衡。 由于化学势的绝对值不知道，所以不能用化学势来检验一个化学反应是否达到平衡，而是用 动力学方法来判断是否平衡 二、为什么化学反应通常不能进行到底？ 实际的化学反应进行时，总是反应物与产物混合条件下进行，这样随着反应进行各组分的浓 度随反应进度的改变而改变，所以各物质的化学势是反应进度的函数 随着反应进行，反应物浓度减少（化学势减小），产物浓度增加（化学势增加），达到某浓度 时各个反应物的化学势与其计量系数乘积之和等于各个产物的化学势与其计量系数乘积之 和时反应达平衡，这就是化学反应总是存在平衡的原因。 所以说严格讲，反应物与产物处于同一体系的反应都是可逆的，不能进行到底。 只有逆反应与正反应相比小到可以忽略不计的反应， 可以粗略地认为可以进行到底

3 用 判断，这相当于 图上曲线的斜率，因为是微小变化，反应进度处于 0~1 mol 之间。 反应自发向右进行，趋向平衡 反应自发向左进行，趋向平衡 反应达到平衡 由此可见：化学反应平衡的本质 从动力学看是正逆反应速率相等 从热力学看，当各个反应物的化学势与其计量系数乘积之和等于各个产物的化学势与其计量 系数乘积之和时反应达平衡。 由于化学势的绝对值不知道，所以不能用化学势来检验一个化学反应是否达到平衡，而是用 动力学方法来判断是否平衡 二、为什么化学反应通常不能进行到底？ 实际的化学反应进行时，总是反应物与产物混合条件下进行，这样随着反应进行各组分的浓 度随反应进度的改变而改变，所以各物质的化学势是反应进度的函数。 随着反应进行，反应物浓度减少（化学势减小），产物浓度增加（化学势增加），达到某浓度 时各个反应物的化学势与其计量系数乘积之和等于各个产物的化学势与其计量系数乘积之 和时反应达平衡，这就是化学反应总是存在平衡的原因。 所以说严格讲，反应物与产物处于同一体系的反应都是可逆的，不能进行到底。 只有逆反应与正反应相比小到可以忽略不计的反应， 可以粗略地认为可以进行到底。 , ( )T p G    G ~  , ( ) 0 T p G     , ( ) 0 T p G     , ( ) 0 T p G   = 

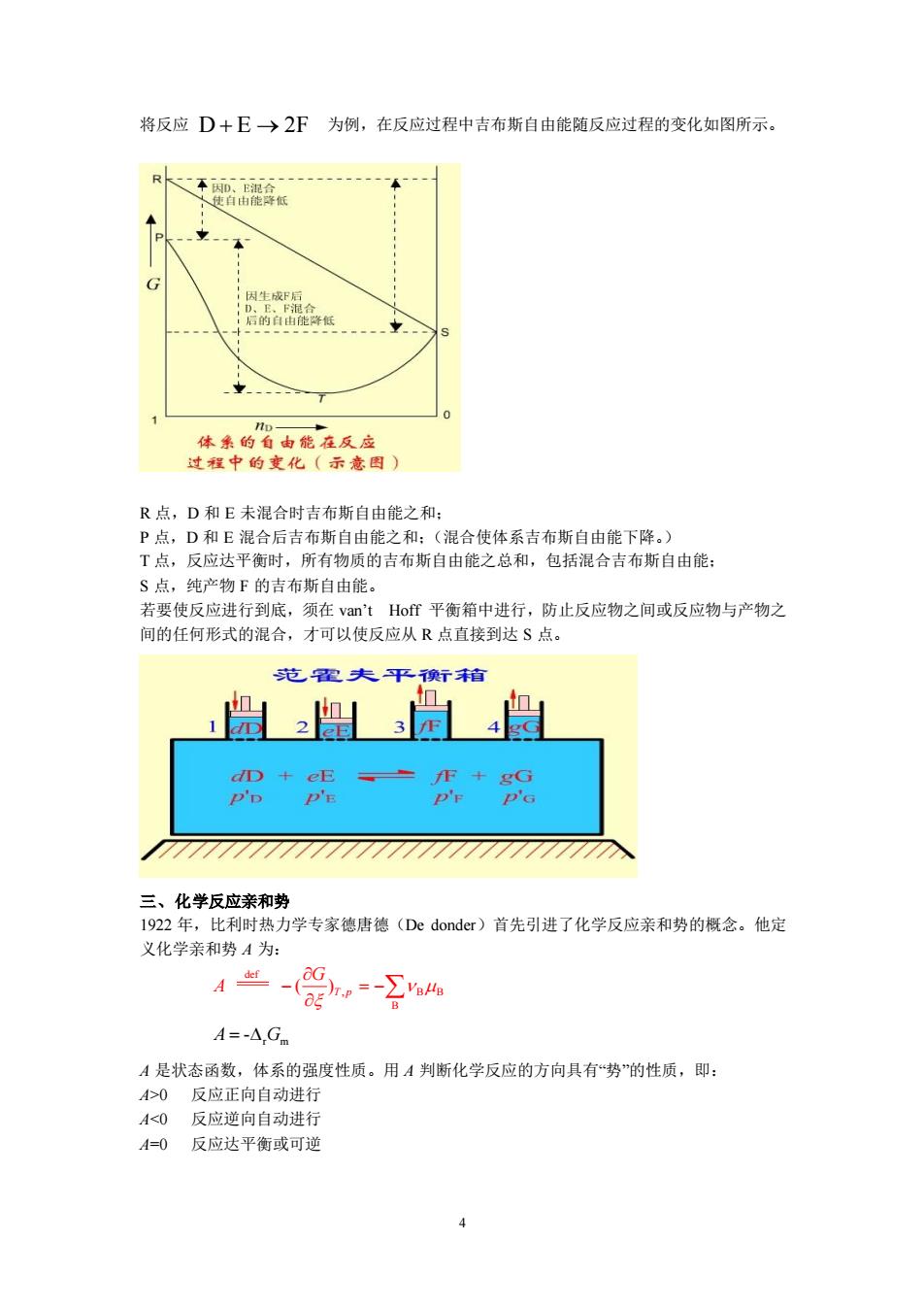
将反应D+E→2F为例，在反应过程中吉布斯自由能随反应过程的变化如图所示。 R 体米的自由能在反应 过程中的变化（示意图 R点，D和E未混合时吉布斯自由能之和： P点，D和E混合后吉布斯自由能之和：（混合使体系吉布斯自由能下降。） T点，反应达平衡时，所有物质的吉布斯自由能之总和，包括混合吉布斯自由能 S点，纯产物F的吉布斯自由能。 若要使反应进行到底，须在van'tHof平衡箱中进行，防止反应物之间或反应物与产物之 间的任何形式的混合，才可以使反应从R点直接到达S点。 范配夫平衡际箱 盟 D+e产P+G P'p P'E 777777777777777777777777777の 三、化学反应亲和势 1922年，比利时热力学专家德唐德(De donder)首先引进了化学反应亲和势的概念。他定 义化学亲和势4为： 4-，=- A=-△，Gm A是状态函数，体系的强度性质。用A判断化学反应的方向具有“势”的性质，即： A>0反应正向自动进行 A<0反应逆向自动进行 A=0反应达平衡或可逆

4 将反应 为例，在反应过程中吉布斯自由能随反应过程的变化如图所示。 R 点，D 和 E 未混合时吉布斯自由能之和； P 点，D 和 E 混合后吉布斯自由能之和；（混合使体系吉布斯自由能下降。） T 点，反应达平衡时，所有物质的吉布斯自由能之总和，包括混合吉布斯自由能； S 点，纯产物 F 的吉布斯自由能。 若要使反应进行到底，须在 van’t Hoff 平衡箱中进行，防止反应物之间或反应物与产物之 间的任何形式的混合，才可以使反应从 R 点直接到达 S 点。 三、化学反应亲和势 1922 年，比利时热力学专家德唐德（De donder）首先引进了化学反应亲和势的概念。他定 义化学亲和势 A 为： A 是状态函数，体系的强度性质。用 A 判断化学反应的方向具有“势”的性质，即： A>0 反应正向自动进行 A<0 反应逆向自动进行 A=0 反应达平衡或可逆 D E 2F + → def , B B B ( )T p G A     − = −   r m A G = -

§6.2化学反应的平衡常数和等温方程式 1、理相气体反应的热力学平衡常数 理想气体之间反应，反应物与产物混合，各组分的分压服从道尔顿定律，其中某一组分的化 学势为； (T,p)=店(T)+RTnB 将其代入 4G=∑y4 A,G.=∑层+RTΠ3r 是交的标雅果尔本布斯香版交 4,G8=∑yA层 压力商 Q=Π哈” 化学反应等温方程 △，Gn=△.Ge+RTInQ, 反应达平衡时，Qp=K9 △，G=-RTInK K9是指压力的标准态为P反应达平衡时的平衡常数，所以叫标准平衡常数或热力学平衡 常数，与压力无关，与温度、标准态的选择及反应方程式的写法有关。 由此可见， 个化学反应△rGm与反应的方向有关，△rGm0与反应的限度有关 (a)若Kp>Qr时，△rGm0,反应自右向左自发进行 (c)若KpP=Oe时.△rGm=0.反应达平衡。 2、非理想气体反应的等温方程式 若反应气体是非理想气体，则用逸度表示 (T,p)=后(T)+RTIn 对于化学反应 dD+eE+.→gG+hH+ 将化学势表示式代入（△，Gn)p的计算式：（△，G)p=∑Ma △，Gn=A,G(+RTn6/p'P. (f61p3)f1p)° =△，Ga(T)+RTInQ

5 §6.2 化学反应的平衡常数和等温方程式 1、理想气体反应的热力学平衡常数 理想气体之间反应，反应物与产物混合，各组分的分压服从道尔顿定律，其中某一组分的化 学势为： 将其代入 反应的标准摩尔吉布斯函数变 定义: 压力商 化学反应等温方程 反应达平衡时,Qp=KP Ө KP Ө 是指压力的标准态为 P Ө 反应达平衡时的平衡常数，所以叫标准平衡常数或热力学平衡 常数，与压力无关，与温度、标准态的选择及反应方程式的写法有关。 由此可见，一个化学反应ΔrGm 与反应的方向有关，ΔrGmӨ 与反应的限度有关 （a)若 KP Ө>QP时， ΔrGm 0，反应自右向左自发进行 （c)若 KP Ө=QP时, ΔrGm =0,反应达平衡。 2、非理想气体反应的等温方程式 若反应气体是非理想气体,则用逸度表示 对于化学反应 将化学势表示式代入 的计算式： B B B ( , ) ( ) ln P T p T RT p   = + $ $ r m B B B  = G   B B r m B B B ln ( ) p G RT p   = +     r m B B B  = G   B B B Q ( ) P p p  =  $ r m r m ln  =  + G G RT Qp ln r P m  = − G RT K $ $ B B B ( , ) ( ) ln f T p T RT p   = + $ $ d e g h D E G H + + → + + rGm T , p ( ) r m , B B B ( )  = G T p   g h G H r m r m d e D E ( / ) ( / ) ( ) ln ( / ) ( / ) f p f p G G T RT f p f p  =  + $ $ $ $ $ r m =  + G T RT Q ( ) ln f $

这就是非理想气体化学反应等温方程式。Q,称为逸度商”，可以通过各物质的逸度求算 △，G(T值也可以通过多种方法计算，从而可得△，G。的值。 △，G(T)称为化学反应标准摩尔Gibs自由能变化值，只是温度的函数，与反应方程式写 法和标准态有关。 非理想气体反应的热力学平衡常数 当体系达到平衡，△，Gm=0 ，则 A.G(T)=-RTIn (s )(s )". =-RTInK (f1p)(fE1p)° K;称为热力学平衡常数，它仅是温度的函数，与反应方程式写法有关。在数值上等于 平衡时的逸度商”，是量纲为1的量，单位为1。因为它与标准化学势有关，所以又称为标 准平衡常数 非理想气体反应的化学反应等温式可表示为： △，Gm=-RTIn K+RTInO Ki>O A,G 0 反应向左自发进行 K= △Gm=0 反应达平衡 3、均相液相反应的平衡常数 均相液相反应的平衡常数表大式与气相反应的类似，只是标准态不同 (1)若反应物和产物均为液相，若是理想液态混合物，则各组分等同对待，任一组分的化 学势可表示为： ug =u RTInxa 因为液体的化学势受压力的影响不大 a=g+∫"dP≈ Hg=+RT Inxg=+RT Inxg 对于反应dD(L)+eE(L)FgGL+F(U △，Gn=Eya4a≈g(店+RTInxG)+f+RTInxe) -d+RTinx,)-e店+RTInxe)=△，G+RTin 平衡时 △，G=-RTIn K (2)若为非理想液态混合物，用活度表示 △，G=-RTIn K 6

6 这就是非理想气体化学反应等温方程式。 称为“逸度商”，可以通过各物质的逸度求算 值也可以通过多种方法计算，从而可得 的值。 称为化学反应标准摩尔 Gibbs 自由能变化值，只是温度的函数，与反应方程式写 法和标准态有关。 非理想气体反应的热力学平衡常数 当体系达到平衡， ，则 称为热力学平衡常数，它仅是温度的函数,与反应方程式写法有关。在数值上等于 平衡时的“逸度商”，是量纲为 1 的量，单位为 1。因为它与标准化学势有关，所以又称为标 准平衡常数。 非理想气体反应的化学反应等温式可表示为： 反应向右自发进行 反应向左自发进行 反应达平衡 3、均相液相反应的平衡常数 均相液相反应的平衡常数表达式与气相反应的类似，只是标准态不同。 （1）若反应物和产物均为液相,若是理想液态混合物，则各组分等同对待，任一组分的化 学势可表示为： 因为液体的化学势受压力的影响不大 对于反应 dD(L)+eE(L)=gG(L)+fF(L) 平衡时 （2）若为非理想液态混合物，用活度表示 g h G H r m d e D E ( / ) ( / ) ln ( / ) ) ) ( / ( f p f p RT f p f T p  G = − $ $ $ $ $ = −RT K ln f $ Qf r m  G T( ) $ rGm r m  G T( ) $ rGm = 0 K f $ r m  = − + G RT K RT Q ln ln f f $ K Q G f f    r m 0 $ K Q G f f    r m 0 $ K Q G f f =  = r m 0 $ ln   B B B RT x  = + P B B m B P    V dP  = +   $ $ $ ln ln    B B B B B RT x RT x  = +  + $ ( ln ) ( ln ) ( ln ) ( ln ) ln r m B B G G F F f g F G D D E E r m d e D E G g RT x f RT x x x d RT x e RT x G RT x x        =   + + + − + − + =  + $ $ $ $ $ ln  = − r m x G RT K $ $ ln  = − r m a G RT K $ $

§6.3平衡常数的表示式 经验平查常数 反应达平衡 ,用反应物和生成物的实际压力、摩尔分数或浓度代入计算，得到的平衡常数 称为经验平衡常数，一般有单位。例如，对任意反应： dD+eE+.→gG+hH+. 1.用压力表示的经验平衡常数 K。-5哈=哈 P哈p呢. Kp= -=Kpps-Ev 理想气体的KP只是温度的函数 (y 一= -=Kpk ps-Eva 因为K是温度和压力的函数所以非理想气体K氵是温度和压力的函数 2.用摩尔分数表示的平衡常数 对理想气体，符合Dalton分压定律P=pxB 水=太，p =K,pw=Kp3p=（号 D Kx不仅与温度有关，还与压力有关 3.用物质的量浓度表示的平衡常数 k=%二-哈 c8·C

7 §6.3 平衡常数的表示式 经验平衡常数 反应达平衡时，用反应物和生成物的实际压力、摩尔分数或浓度代入计算，得到的平衡常数 称为经验平衡常数，一般有单位。例如，对任意反应： 1. 用压力表示的经验平衡常数 理想气体的 KP 只是温度的函数 因为 Kr 是温度和压力的函数,所以非理想气体 是温度和压力的函数 2.用摩尔分数表示的平衡常数 对理想气体，符合 Dalton 分压定律 Kx 不仅与温度有关,还与压力有关 3．用物质的量浓度表示的平衡常数 d e g h D E G H + + → + + G H B d B B D E g h p e p p K p p p   = =   H G E D ( ) ( ) ( ) ( ) B h g P P e d P P p p K K p P P p p −  = = $ $ $ $ $ $ H H G G E D E D ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) B h g h g H G f P r e d e d E D f P r f P r p p p p K K K p f f P r P r p p p p −  = = = $ $ $ $ $ $ $ $ $ $ K f $ G H B B B D E g h x d e x x K x x x   = =   B B p px = B B K K p x p − = H G E D ( ) ( ) ( ) ( ) B h g P P e d P P p p K K p P P p p −  = = $ $ $ $ $ $ B B B B ( ) B x x p K p p K p   −    = = $ $ G H B B B D E g h c d e c c K c c c   = =  

对理想气体，p=cRT ry K.=RT R K(R) 4.液相反应用活度表示的平衡常数 K。=Ia哈 d Yacp K。=K。·K,Π(c)a 平衡常数与化学方程式写法的关系 A,Gs(T)=-RTIn K 下标m表示反应进度为1mol时的标准Gibbs自由能的变化值。显然，化学反应方程中计 量系数呈倍数关系，△，G(T的值也呈倍数关系，而K值则呈指数的关系。 例如：H,(g)+1,(g)=H(g) H2(g+l2(g=2H(g) △，G22=2A,G K2=(K)月 §6.4复相化学平衡 1、什么叫复相化学反应？ 有气相和凝聚相（液相、固体）共同参与的反应称为复相化学反应。 例如，有下述反应，并设气体为理想气体： CaCO,(s)>CaO(s)+CO,(g) K p(CO,)/p p(CO2)称为CaCO,(s)的解高压力。 只考虑凝聚相是纯态的情况，由于压力对凝聚相的化学势影响不大，压力为P时纯态的化 学势约等于它的标准态化学势，所以复相反应的热力学平衡常数只与气态物质的压力有关。 2、解离压力(dissociatio ra) 某因体物质发生解离反位时”所产生气体的压力，称为解离压力，是然这压力在定温下有定 值。 如果产生的气体不止一种，则所有气体压力的总和称为解离压力。 NH,HS(s)=NH,(g)+H.S(g) p=p(NH)+p(H2S) 力学平衡常数K-pNH.PHS)=p/py 8

8 对理想气体， 4．液相反应用活度表示的平衡常数 平衡常数与化学方程式写法的关系 下标 m 表示反应进度为 1 mol 时的标准 Gibbs 自由能的变化值。显然，化学反应方程中计 量系数呈倍数关系， 的值也呈倍数关系，而 值则呈指数的关系。 例如： §6.4 复相化学平衡 1、什么叫复相化学反应？ 有气相和凝聚相（液相、固体）共同参与的反应称为复相化学反应。 例如，有下述反应，并设气体为理想气体： 称为 的解离压力。 只考虑凝聚相是纯态的情况，由于压力对凝聚相的化学势影响不大，压力为 P 时纯态的化 学势约等于它的标准态化学势，所以复相反应的热力学平衡常数只与气态物质的压力有关。 2、解离压力（dissociation pressure） 某固体物质发生解离反应时，所产生气体的压力，称为解离压力，显然这压力在定温下有定 值。 如果产生的气体不止一种，则所有气体压力的总和称为解离压力。 则热力学平衡常数 p = cRT B B ( ) ( ) ( ) ( ) ( ) G g f F c p E D e d P P RT RT K K RT P P RT RT − = = B B B K a a  =  B B B c a c  = $ B B ( ) K K K c a c r − =   $ r m  = − G T RT K ( ) ln f $ $ r m G T( ) $ K f $ 1 1 2 2 H (g) I (g) HI(g) 2 2 + = H (g) I (g) 2HI(g) 2 + 2 =  =  r m,2 r m,1 G G 2 $ $ 2 ,2 ,1 ( ) K K f f = $ $ CaCO (s) CaO(s) CO (g) 3 2 → + 2 (CO )/ K p p p = $ $ (CO ) p 2 CaCO (s) 3 NH HS(s) NH (g) H S(g) 4 = 3 + 2 (NH ) (H S) p = p 3 + p 2 3 2 (NH ) (H S) p p p p K p =  $ $ $ 1 2 4 = ( / ) p p $

§65标准摩尔生成古布斯自由能 1、标准状态下反应吉布斯自由能的变化值 在温度为T时，当反应物和生成物都处于标准态，发生反应进度为1mal的化学反应Gibbs 自由能的变化值，称为该反应的标准摩尔反应吉布斯自由能变化值△，G △G的用途 (1)计算热力学平衡常数 △G=-RT In Ks K=exp(-△，GIRT) (2)用赫斯定律计算实验不易测定的平衡常数 例如，求C(S)+02(g)→CO(g) 的平衡常数 (1)C(s)+O2(g)→C02(g) △G0(①) (2)C0(g)+02(g)→C02(g)△，G(2) (1)-(2)得(3) (3)C(s)+02(g)→C0(g) △.Gm(3) △，G(3)=A,G(1)-△，G(2) K(3)= K(1) K(2) (3)近似估计反应的可能性 只能用AG 判断反应的方向。但是，当△，G日的绝对值很大时，基本上决定 AG的所可以用米近伤什发位的司可能。 -般认为a)当△，G品>41.84KJ·m01 反应不能正向进行 A之时n (心)当△，G。=0反应可能性存在 （仙当△，G品<0反应有可能性进行，平衡位置对产物的生成有利。 尤其是在有机合成中，可能有若干条路线，用计算 (④用A,G值求出热力学平衡常数K值。根据K与温度的关系（后达.可以 决定用升温还是降温的办法反应顺利进行。 2、标准摩尔生成吉布斯自由能△，G 对于化学反应，若知道反应物和产物的摩尔吉布斯自由能，就可以计算△，G,就可以求 出平衡常数，但吉布斯自由能的绝对值不知道，使这种方法不可能。 解决的方法：用相对标准，即将标准压力下稳定单质（包括纯理想气体，纯周体或液体）的 生成吉布斯自由能看作零，则：

9 §6.5 标准摩尔生成吉布斯自由能 1、标准状态下反应吉布斯自由能的变化值 在温度为 T 时，当反应物和生成物都处于标准态，发生反应进度为 1 mol 的化学反应 Gibbs 自由能的变化值，称为该反应的标准摩尔反应吉布斯自由能变化值 的用途 （1）计算热力学平衡常数 （2）用赫斯定律计算实验不易测定的平衡常数 例如，求 的平衡常数 (1) - (2) 得（3） （3）近似估计反应的可能性 只能用 判断反应的方向。但是，当 的绝对值很大时， 基本上决定 了 的值，所以可以用来近似地估计反应的可能性。 一般认为(a)当 反应不能正向进行 (b)当 存在着改变外界条件使反应向更有利于生成产物方向转化的可能性； （c）当 反应可能性存在 (d) 当 反应有可能性进行，平衡位置对产物的生成有利。 尤其是在有机合成中，可能有若干条路线，用计算 的方法，看那条路线的值最小， 则可能性最大。若 是一个很大的正数，则该反应基本上不能进行。 （4） 用 值求出热力学平衡常数 值。根据 与温度的关系（后述），可以 决定用升温还是降温的办法反应顺利进行。 2、标准摩尔生成吉布斯自由能 对于化学反应，若知道反应物和产物的摩尔吉布斯自由能，就可以计算 ，就可以求 出平衡常数，但吉布斯自由能的绝对值不知道，使这种方法不可能。 解决的方法：用相对标准，即将标准压力下稳定单质（包括纯理想气体，纯固体或液体）的 生成吉布斯自由能看作零，则： r m G $ r m G $ r m  = − G RT K ln a $ $ r m exp( / ) K G RT a = − $ $ 1 C(s) O (g) CO(g) + → 2 2 2 2 r m (1) C(s) O (g) CO (g) (1) + →  G $ 1 2 2 2 r m (2) CO(g) O (g) CO (g) (2) + →  G $ 1 2 2 r m (3) C(s) O (g) CO(g) (3) + →  G $ r m r m r m  =  −  G G G (3) (1) (2) $ $ $ (1) (3) (2) p p p K K K = $ $ $ r m , , f 0 ( )  G T p w = r m G $ rGm 1 r m G KJ mol 41.84 −  • $ 1 r m G KJ mol 41.84 0 −  − − • $ 在 之间时 r m  = G 0 $ r m  G 0 $ r m G $ r m G $ r m G $ K $ K $ f m G $ r m G $

在标准压力下，由稳定单质生成1ml某物质时吉布斯自由能的变化值，称为该物质的标准 摩尔生成吉布斯自由能，用下述符号表示： △，G(化合物，物态，温度) 通常在298.15K时的值有表可查。483页表16 3、离子的标准廉尔生成吉布斯自由能 △，G(H,ag,m=1 mol.kg")=0 规定水溶液中，氢离子的浓度为 =I mol 并且指定 H (H',ag.m=1 mol.kg)=0 Ss (H'ag.m=1 mol-kg)=0 4、△，G数值的用处 利用，G数值计算化学反应的△，G △G品的值在定义时没有规定温度，通常在298.15K时的数值有表可查，利用这些 表值，我们可以计算任意反应在298.15K时的△，G A,G=∑yA,G(B) 如反应dD+eE=F+gG △，G=gA,G2(G)+f△，G(F)-d△，G(D)-A,G(E) §6.6温度、压力及情性气体对化学平衡的影响 1 温度对化学平衡的影响 理想气体：△，G=-RTIn K 根据吉布斯一亥姆霍兹方程 △.H T2 a△G) a(-RTInK T aT =-4 van't Hoff公式的徽分式 din K. dr RT 对吸热反应，△，H>0，升高温度，K增加，对正反应有利

10 在标准压力下，由稳定单质生成 1 mol 某物质时吉布斯自由能的变化值，称为该物质的标准 摩尔生成吉布斯自由能，用下述符号表示： （化合物，物态，温度） 通常在 298.15 K 时的值有表可查。483 页表 16 3、离子的标准摩尔生成吉布斯自由能 有离子参加的反应，主要是电解质溶液。溶质的浓度主要用质量摩尔浓度表示，用的标准态 是 且具有稀溶液性质的假想状态，这时规定的相对标准为： 规定水溶液中,氢离子的浓度为 时标准摩尔生成吉布斯自由能为零,由 此而得到其他离子的标准摩尔生成吉布斯自由能的数值 并且指定 4、 数值的用处 利用 数值计算化学反应的 的值在定义时没有规定温度，通常在 298.15 K 时的数值有表可查，利用这些 表值，我们可以计算任意反应在 298.15 K 时的 如反应 dD+eE=fF+gG §6.6 温度、压力及惰性气体对化学平衡的影响 1、温度对化学平衡的影响 理想气体： 根据吉布斯—亥姆霍兹方程 van’t Hoff 公式的微分式 对吸热反应， ，升高温度， 增加，对正反应有利。 f m G $ -1 m =  1 mol kg $ -1 f m G aq m (H , , 1 mol kg ) 0 +  =  = $ -1 m =  1 mol kg -1 f m H aq m (H , , 1 mol kg ) 0 +  =  = $ -1 S (H , , 1 mol kg ) 0 aq m + =  = $ f m G $ f m G $ r m G $ f m G $ r m G $ r m B f m B  =  G G  (B) $ $ ( ) ( ) ( ) ( )  =  +  −  −  r m f m f m f m f m G g G G f G F d G D e G E $ $ $ $ $ ln p  = − r m G RT K $ $ 2 ( ) [ ] r m r m P G T H T T    = −  $ $ 2 ln ( ) ( ) [ ] [ ] r m P r m P P G RT K T T H T T T  −    = − = −   $ $ $ r m 2 dln d Kp H T RT  = $ $ r m   H 0 $ K p $