新疆大学：《物理化学》课程授课教案（讲义）第一章 气体（主讲：刘月娥）

物理化学教案 新疆大学化学化工学院物理化学教研室 刘月娥 第一章气体 聚集状态一物质的聚集状态通常有气、固、液三种状态。在研究放电管中电离气体 的性质时，发现了一表 新的导电流体， (包括带正负电荷的离子、电子以及少量未经电离的 分子、原子等，整体呈电中性，故称为等离子体。 被称为物质的第四态。另外有人把超高 压、超高温下的状态称为第五态。此外还有超导态、超流态等等。 历史上人们对气态物质的性质研究的比较多，获得了许多经验定律，然后对气体分子 的运动设计微观运动模型，从理论的角度深入研究气体分子运动的规律一一即从宏观到微 观并利用徽观图像使宏观现象得到解释 1.1气体分子动理论 对于气体在低压及较高温度下的行为，在历史上曾经归钠出一些经验定律：波义尔 (R.Bolye,.1662)定律，盖吕萨克(U.Ga-Lussac,1808)定律等。从这些经验定律可以导出低 压下气体的P、V、T之间的关系式p=mRT。 这种群系压力 、体积和温度 者间的关系式称为状态方程式。我们把在任何压力任何温 度下都能严格遵从pV=RT的气体叫做理想气体。此式又叫做理想气体的状态方程式 理想气体实际上是一个科学的抽象概念，客魂上并不存在，它只能看作是实际气体在压 力很低时的一种极限状况。 ,气体分子动理论的基太公式 为进 步说 为什么理想气体的P、V、T之间会具有Ψ nRT这样简单的关系，人们 根据对宏观现象的认识，提出了分子运动的微观模型，然后根据所设想的运动棋型来推导 运动的规律。如果据此所推出的结论与实验事实相符，则说明所设想的模型是合理正确的，经 反复考验缘正后即可上升为理论。 1、气体 分子运动的微观模型动理论P10-11 量分 子的集合体 ,相对于分子与分子间的距离以及整个容器的体积来说，气 体分子本身的体积是很小的，可以忽略不计，因此常可以将气体分子当作质点来处理。 (2)气体分子不断地作无规则的运动，均匀分布在整个容器之中 (3)分子彼此的碰靠以及分子与器壁的碰撞是完全弹性的（即在碰章前后总动量不损失）。 2、气体分子动理论的基本方程式 根据气体分子动理论微观模型)所导出的基本方程式 PV=l/3mNμ 推导过程P) 式中P是N个分子与器壁碰撞后所产生的总效应，它具有统计平均的意义 式中根均方速率μ，也是一个徽观量的统计平均值，它不能由实验直接测量， 而P和V则是可以直接由实验量度的宏观量。 因此式PV=1/3mNu2 是联系宏观可测量与微观不可测量之间的桥梁 二、压力和温度的统计概念 1、压力的统计平均意义（压力定义见P)

1 物 理 化 学 教 案 新疆大学化学化工学院物理化学教研室 刘月娥 第一章 气体 聚集状态-物质的聚集状态通常有气、固、液三种状态。在研究放电管中电离气体 的性质时，发现了一种新的导电流体，(包括带正负电荷的离子、电子以及少量未经电离的 分子、原子等，整体呈电中性，故称为等离子体。 )被称为物质的第四态。另外有人把超高 压、超高温下的状态称为第五态。此外还有超导态、超流态等等。 历史上人们对气态物质的性质研究的比较多，获得了许多经验定律，然后对气体分子 的运动设计微观运动模型，从理论的角度深入研究气体分子运动的规律-即从宏观到微 观并利用微观图像使宏观现象得到解释 1.1 气体分子动理论 对于气体在低压及较高温度下的行为，在历史上曾经归纳出一些经验定律:波义尔 (R.Bolye, 1662)定律，盖·吕萨克(J. Gay-Lussac, 1808)定律等。从这些经验定律可以导出低 压下气体的 P、V、T 之间的关系式 pV = nRT。 这种联系压力、体积和温度三者间的关系式称为状态方程式。我们把在任何压力任何温 度下都能严格遵从 pV = nRT 的气体叫做理想气体。此式又叫做理想气体的状态方程式。 理想气体实际上是一个科学的抽象概念，客观上并不存在，它只能看作是实际气体在压 力很低时的一种极限状况。 一. 气体分子动理论的基本公式 为进一步说明为什么理想气体的 P、V、T 之间会具有 pV = nRT 这样简单的关系，人们 根据对宏观现象的认识，提出了分子运动的微观模型，然后根据所设想的运动模型来推导 运动的规律。如果据此所推出的结论与实验事实相符,则说明所设想的模型是合理正确的,经 反复考验修正后,即可上升为理论。 1、气体分子运动的微观模型(动理论)P10-11 (1)气体是大量分子的集合体。相对于分子与分子间的距离以及整个容器的体积来说，气 体分子本身的体积是很小的，可以忽略不计，因此常可以将气体分子当作质点来处理。 (2)气体分子不断地作无规则的运动，均匀分布在整个容器之中 (3)分子彼此的碰撞以及分子与器壁的碰撞是完全弹性的(即在碰撞前后总动量不损失）。 2、气体分子动理论的基本方程式 根据气体分子动理论(微观模型)所导出的基本方程式 PV=1/3mNμ2 (推导过程 P11-14) 式中 P 是 N 个分子与器壁碰撞后所产生的总效应，它具有统计平均的意义。 式中根均方速率μ，也是一个微观量的统计平均值，它不能由实验直接测量。 而 P 和 V 则是可以直接由实验量度的宏观量。 因此式 PV=1/3mNμ2 是联系宏观可测量与微观不可测量之间的桥梁。 二、压力和温度的统计概念 1、压力的统计平均意义(压力定义见 P12)

()对于气体中的某一个分子来说，它与器壁的碰撞是不连续的，而且它的速度也因分子间 的互相碰撞而不断地变化，所以个别分子与器壁碰撞时，在单位时间、单位体积上所引起 的动量变化是起代不定，但由于气体是大量分子的集合， 尽管个别分子的动量变化起伏不 定，但是平均压力却是一个定位，并且是一个宏观可测的物理量。 (2)根均方速率“，是一个统计平均数值，它与各个分子的速率有关，但又不等于任何单个 分子的速率。所以压力是大量分子集合所产生的总效应。 2、温度的统 含藏 子的平 平动能®=12mμ2和温度具有平行的关系，温度越高则分子的平均动能 就越大，可写成 1/2m42-fm 温度与大量分子的平均平动能具有函数的关系，所以温度也具有宏观的统计概念。 三、气体分子运动公式对几个经验定律的说明 如 气体分子动理论所提出的关于分子运动的模型以及由此而导出的气体分子运动公 式是对的，则能够对一些经验规律给以说明。 1、Boyle-Marriote定律 将PV=13mNu2写作PV=12mu2,N,2/3对于一定量的气体，在定温下，N和12mu2 均为定值。所以上式可写作PV=C。 即定温下 定量的气 体，其体积与压力成反比 ,这个定律最初是在低压下由实验所总结出来的经验规律 。(结论 与实验事实相符) 2、Charles-GaV-Lussac定律 温度越高分子的平动能越大12mμ2=fT 低压下实验表明 P具有线性关系，根据分子动理论PV=13mN?故而可得分子的平 动能与t也具有线性关系 。设温度在0C和t时平均平动能分别是E和配 则E=Bw(l+at) 根据气体分子动理论的公式，在0C和t时， ,= 馆 2 Vo-3p -3p NEa 则y,=%1+a) 式中a就是体膨胀系数。令T=t+1/a则Vt=V0Ta=CT 即对定量的气体，在定压下，体积和T成正比，这就是Charles-Gay-Lussac定律。 3 Avogadro定律 任意两种气体当温度相同时，具有相等的平均平动能1/2mu?-12mμ： 从分子运动公式 p=Nm=子m)

2 (1)对于气体中的某一个分子来说，它与器壁的碰撞是不连续的，而且它的速度也因分子间 的互相碰撞而不断地变化，所以个别分子与器壁碰撞时，在单位时间、单位体积上所引起 的动量变化是起伏不定。但由于气体是大量分子的集合，尽管个别分子的动量变化起伏不 定，但是平均压力却是一个定值，并且是一个宏观可测的物理量。 (2)根均方速率μ，是一个统计平均数值，它与各个分子的速率有关，但又不等于任何单个 分子的速率。所以压力是大量分子集合所产生的总效应。 2、温度的统计含意 由于分子的平均平动能(Ēt=1/2 mμ2 )和温度具有平行的关系，温度越高则分子的平均动能 就越大，可写成： 1/2 mμ2 =ƒ(T) 温度与大量分子的平均平动能具有函数的关系，所以温度也具有宏观的统计概念。 三、气体分子运动公式对几个经验定律的说明 如果气体分子动理论所提出的关于分子运动的模型以及由此而导出的气体分子运动公 式是对的，则能够对一些经验规律给以说明。 1、Boyle-Marriote 定律 将 PV=1/3mNμ2 写作 PV=1/2mμ2 •N•2/3 对于一定量的气体，在定温下，N 和 1/2mμ2 均为定值。所以上式可写作 PV=C。 这就是 Boyle-Marriote 定律。 即定温下一定量的气 体，其体积与压力成反比。这个定律最初是在低压下由实验所总结出来的经验规律。（结论 与实验事实相符） 2、Charles-Gay-Lussac 定律 温度越高分子的平动能越大Ēt=1/2 mμ2 = ƒ(T) 低压下实验表明 PV-t 具有线性关系，根据分子动理论 PV=1/3mNμ2故而可得分子的平 动能与 t 也具有线性关系。设温度在 0 0C 和 t 时平均平动能分别是Ēt0 和Ētt 则 Ētt=Ēt0(1+at) 根据气体分子动理论的公式，在 0 0C 和 t 时， 式中α就是体膨胀系数。令 T=t+1/α 则 Vt=V0Tα=C’T 即对定量的气体，在定压下，体积和 T 成正比，这就是 Charles-Gay-Lussac 定律。 3、Avogadro 定律 任意两种气体当温度相同时，具有相等的平均平动能 1/2 m1μ1 2 =1/2 m2μ2 2 从分子运动公式 2 , 1 2 3 3 V Nm NE t t t t p p = =  2 0 0 ,0 1 2 3 3 V Nm NEt p p = =  0 (1 ) 则V V t t = + 2 2 1 1 1 1 1 1 1 1 1 2 1( ) 3 3 2 p V N m N m = =  

p=Nm店=N,(m) 因此在同温、同压下，同体积的气体应有NN: 即同温同压下，同体积的各种气体所含有的分子个数相同，这就是Avogadro定律 4、理想气体的状态方程式 由气体分子的运动模型导出了上面三个定律，则合并后就可等到理翘气体的状态方程式。 PV=nRT. V=f(P,T,N) 假r-微 对于一定量的气体，N为常数，dN0,所以， -()(r 根据Boyle-Marriote定律， r- )日 根据Charles-Gay-Lussac定律， V=CT c-号 代入上式后得 aw=-5r+号n av 上式积分得 lnV+Hnp=nT+常数 若所取气体的量是1mol,则体积写作Vm,常数写作R,即得PV=RT 上式两边同乘以物质的量，则得 PV-nRT 5、Dalton分压定律 若在定温下，把几种不同的气体混合于容积为V的容器中，各种分子的数目分别为N,2, .,总分子数为N+八2+=N。混合气体可设想是通过如下的混合过程来完成

3 因此在同温、同压下，同体积的气体应有 N1=N2 即同温同压下，同体积的各种气体所含有的分子个数相同，这就是 Avogadro 定律 4、理想气体的状态方程式 由气体分子的运动模型导出了上面三个定律，则合并后就可等到理想气体的状态方程式， PV=nRT。 V=ƒ(p,T,N) 对于一定量的气体，N 为常数，dN=0，所以， 根据 Boyle-Marriote 定律， 根据 Charles-Gay-Lussac 定律， 代入上式后得 上式积分得 lnV+lnp=lnT+常数 若所取气体的量是 1mol，则体积写作 Vm，常数写作 R，即得 PVm=RT 上式两边同乘以物质的量 n，则得 PV=nRT 5、Dalton 分压定律 若在定温下，把几种不同的气体混合于容积为 V 的容器中，各种分子的数目分别为 N1，N2， ••••••，总分子数为 N1+ N2+ •••=N。混合气体可设想是通过如下的混合过程来完成。 2 2 2 2 2 2 2 2 2 2 1 2 1( ) 3 3 2 p V N m N m = =   T N P N T P , , , V V V dV dP dT dN P T N          = + +                T N P N , , V V dV dP dT P T       = +           C V P = 2 T N, V C V P P P      = − = −    ' V C T = ' P N, V V C T T      = =    V V dV dP dT P T = − + dV dP dT V P T = − +

T,V T,V 十。→ T,V,p=? Ni,pi N2,P2 N1+W2+. 混合前 混合后 混合前， B证Nm片=E 3V 1 2N2E2 B3N,m6=37 诸式相加 ∑R=NE+NE+时 混合后 P= 3V 由于相同温度下，各气体分子具有相同的平均动能，即 E1=E2=.=E Nmx=W1+N2+. 所以 P=P+P+. 这就是Dalton分压定律(Dalton's law of partial pressure)): 即混合气体的总压等于各气体分压之和。 所谓分压，就是在同一温度下，各别气体单独存在、并占有与混合气体相同体积时所具有 的压力。 若任一种气体的分压除以总压，则得 P [2.NE 3*V N -=X 3x V 式中xi是摩尔分数。这是Dalton分压定律的另一种形式

4 诸式相加 混合后 由于相同温度下，各气体分子具有相同的平均动能，即 而 所以 这就是 Dalton 分压定律(Dalton’s law of partial pressure)： 即混合气体的总压等于各气体分压之和。 所谓分压，就是在同一温度下，各别气体单独存在、并占有与混合气体相同体积时所具有 的压力。 若任一种气体的分压除以总压，则得 式中 xi 是摩尔分数。这是 Dalton 分压定律的另一种形式。 混合前 混合后 T, V N1, p1 T, V N2, p2 T, V ,p=? N1 +N2 + ••• + 混合前， + ••• 2 1 1 1 1 1 1 1 2 3 3 N p N m E V V = =  2 2 2 2 2 2 2 1 2 3 3 N p N m E V V = =  1 2 1 2 2 [ ] 3 i i P N E N E V  = + +  2 3 P N E mix mix V = E E E 1 2 = =  = mix N N N mix = + + 1 2 P P P = + + 1 2 2 3 2 3 i i i i i mix mix mix N E P N V x P N N E V      = = =       

6、Amagate(阿马格)分体积定律 在一定的T,P时，混合气体的体积等于组成该混合气体的各组分的分体积之和，即 V=V+V+. 这就是Amagat分体积定律(Amagat's law of partial volune),所谓某一组分的分体积， 它等于该气体在温度T和总压P时单独存在时所占据的体积。 设有两种气体的混合过程如下图所示， T,p T,P T,p N1,V N2,V2 N1+N2,V=? 混合前 V=V+V2 混合后 由此并可导出 2N, E 31 N 2 =X L31 在混合气体中各气体的体积分数就等于它的摩尔分数 四、分子平均平动能与温度的关系 已知气体分子的平均平动能是温度的函数，即 瓦=mr2=f0 根据气体分子运动的基本公式，可以导出与T的定量关系 从Pr=Nm=(mX号M=P(号NW 和PV=NkaT 对一数量为1m0l的分子而言，其平均平动能为 可得E=多R 式中 ko 所以气体分子的平均平动能仅与温度有关，且与热力学温度T成正比。在相同温度下各种 气体分子的平均平动能相等

5 6、Amagat(阿马格)分体积定律 在一定的 T，P 时，混合气体的体积等于组成该混合气体的各组分的分体积之和，即 这就是 Amagat 分体积定律(Amagat’s law of partial volune),所谓某一组分的分体积， 它等于该气体在温度 T 和总压 P 时单独存在时所占据的体积。 设有两种气体的混合过程如下图所示， 混合前 由此并可导出 在混合气体中各气体的体积分数就等于它的摩尔分数 四、分子平均平动能与温度的关系 已知气体分子的平均平动能是温度的函数，即 根据气体分子运动的基本公式，可以导出与 T 的定量关系 对一数量为 1mol 的分子而言，其平均平动能为 式中 所以气体分子的平均平动能仅与温度有关，且与热力学温度 T 成正比。在相同温度下各种 气体分子的平均平动能相等。 T, p N1, V1 T, p N2, V2 T, p N1+N2, V=? + V V V = + + 1 2 混合后 V V V = +1 2 2 3 2 3 i i i i i mix mix mix N E V N P x V N N E P      = = =        1 2 ( ) 2 E m f T t = =  1 1 2 2 2 2 ( )( ) ( ) 3 2 3 3 从PV Nm m N N = = =   和PV Nk T = B 3 2 B 可得Et = k T , 3 2 可得Et m = RT B R k L =

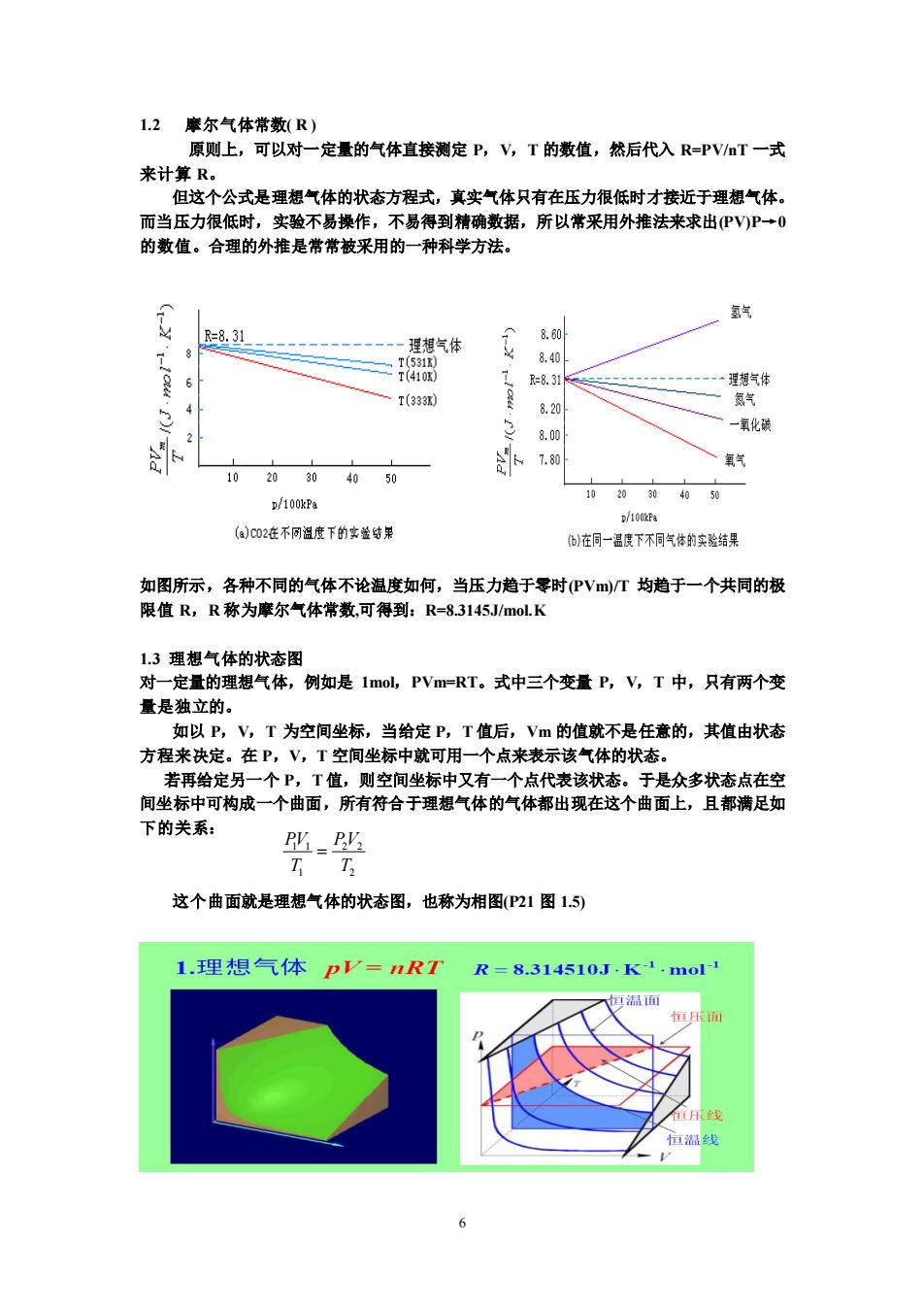
12毫尔气体常数R) 原则上，可以对一定量的气体直接测定P,V,T的数值，然后代入R=PVT一式 来计 但这个公式是理想气体的状态方程式，真实气体只有在压力很低时才接近于理想气体。 而当压力很低时，实验不易操作，不易得到精确数据，所以常采用外推法来求出PV)P→0 的数值。合理的外推是常常被采用的一种科学方法。 复气 一理想气体 8.40 T(333 820 都气 一氧化碳 氧气 1020304050 ()c02在不网温度下的实险结用 在同一温下不同气体的实验结果 如图所示，各种不同的气体不论温度如何，当压力趋于零时PVm)/T均趋于一个共同的极 限值R,R称为摩尔气体常数，可得到：R-83145J/mol.K 13拥想气估的状态图 对一定量的理想气体，例如是1mol,PVm=RT。式中三个变量P,V,T中，只有两个变 量是独立的。 如以P,V,T为空间坐标，当给定P,T值后，Vm的值就不是任意的，其值由状态 方程来决定。在P,V,T空间坐标中就可用一个点来表示该气体的状态。 若再给定另一个P,T值，则空间坐标中又有一个点代表该状态。于是众多状态点在空 间坐标中可构成一个曲面，所有符合于理想气体的气体都出现在这个曲面上， 日都满显加 下的关系： 叱- 这个曲面就是理想气体的状态图，也称为相图(P21图15) 1.理想气体pV=nRT R=8.314510JK1mol 妈温面

6 1.2 摩尔气体常数( R ) 原则上，可以对一定量的气体直接测定 P，V，T 的数值，然后代入 R=PV/nT 一式 来计算 R。 但这个公式是理想气体的状态方程式，真实气体只有在压力很低时才接近于理想气体。 而当压力很低时，实验不易操作，不易得到精确数据，所以常采用外推法来求出(PV)P→0 的数值。合理的外推是常常被采用的一种科学方法。 如图所示，各种不同的气体不论温度如何，当压力趋于零时(PVm)/T 均趋于一个共同的极 限值 R，R 称为摩尔气体常数,可得到：R=8.3145J/mol.K 1.3 理想气体的状态图 对一定量的理想气体，例如是 1mol，PVm=RT。式中三个变量 P，V，T 中，只有两个变 量是独立的。 如以 P，V，T 为空间坐标，当给定 P，T 值后，Vm 的值就不是任意的，其值由状态 方程来决定。在 P，V，T 空间坐标中就可用一个点来表示该气体的状态。 若再给定另一个 P，T 值，则空间坐标中又有一个点代表该状态。于是众多状态点在空 间坐标中可构成一个曲面，所有符合于理想气体的气体都出现在这个曲面上，且都满足如 下的关系： 这个曲面就是理想气体的状态图，也称为相图(P21 图 1.5) 1 1 2 2 1 2 PV PV T T =

1.4分子运动的速率分布 一、Maxwell速率分布定律 本节中所要讨论的问题是 速率落在 一定间隔Y+w内的分子有多少，落在哪一个间隔中的分子数最多： Maxwell于18s9年首先导出了分子速率的分布公式，后来Boltzmann用统计力学的方 法也得到相同的公式。 今设容器内有N个分子，速率在vv+dy范图内的分子有dv个，dNvN表示分子速率 在此范围中的分子占总分子数的分数。对于一个分 子来说，就是该分子的速率在一v+间 隔中的概率 (山)dNv显然与N和dv有关：总分子数越多，速率间隔越大，则dNv必越大。 (2)Nv也与速率v的大小有关，即虽然速率的间隔相同，而速率不同，则其分子数也不同。 dN.o Ndui或dN,=Nf(o)du 书P(1.20) fv:是一个与v及温度有关的函数，称为分布函数(distribution function) 一它的意义相当 于d小v=1时，即速率在V至v+1之间的分子在总分子中所占的分数。 Maxwell证得 将上式代入式1.20)则得Maxwell速率分布公式 P28图1.8是根据上式（书121）所画出的图形，图中纵坐标代表速率介于v至v+1之 间的分子占总分子数的分数，横坐标代表速率。每一条曲线下的面积恒等于1。 当温度升高时，速率的分布曲线变得较宽面平坦，最高点下移。这表明高温时，速率 的分布较宽广。 当温度较低时曲线陡峭，分子速率的分布为集中， 二、分子速率的三个统计平均值-最 然速率、数学平均速率与根均方速率 1、最概然速率：在Maxw速率分布曲线上有一最高点P28图(L8),该点表示具有这种速 率的分子所占的分数最大，这个最高点所对应的速率称之为最橛然速率(vm) 解得 ,2k7 m 或 2RT D.M 式中M为气体的摩尔质量。由此可见，最概然速率与质量的平方根成反比。在相同的温度 下，摩尔质量小的分子，其最概然速率大P2图(13) 2、分子的数学平均速率v:所有分子速率的数学平均值 8kT 3、根均方速率()： >

7 1.4 分子运动的速率分布 一、Maxwell 速率分布定律 本节中所要讨论的问题是: 速率落在一定间隔 v∼v+dv 内的分子有多少，落在哪一个间隔中的分子数最多? Maxwell 于 1859 年首先导出了分子速率的分布公式，后来 Boltzmann 用统计力学的方 法也得到相同的公式。 今设容器内有 N 个分子，速率在 v∼v+dv 范围内的分子有 dNv 个， dNv /N 表示分子速率 在此范围中的分子占总分子数的分数。对于一个分子来说，就是该分子的速率在 v∼v+dv 间 隔中的概率。 (1) dNv 显然与 N 和 dv 有关:总分子数越多，速率间隔越大，则 dNv 必越大。 (2)dNv 也与速率 v 的大小有关，即虽然速率的间隔相同，而速率不同，则其分子数也不同。 f(v):是一个与 v 及温度有关的函数，称为分布函数(distribution function)——它的意义相当 于 dv=1 时，即速率在 v 至 v+1 之间的分子在总分子中所占的分数 。 Maxwell 证得 将上式代入式(1.20)则得 Maxwell 速率分布公式 P28 图 1.8 是根据上式(书 1.21)所画出的图形，图中纵坐标 f(v) 代表速率介于 v 至 v+1 之 间的分子占总分子数的分数，横坐标代表速率。每一条曲线下的面积恒等于 1。 当温度升高时，速率的分布曲线变得较宽面平坦，最高点下移。这表明高温时，速率 的分布较宽广。 当温度较低时曲线陡峭，分子速率的分布为集中。 二、分子速率的三个统计平均值-最概然速率、数学平均速率与根均方速率 1、最概然速率:在 Maxwell 速率分布曲线上有一最高点 P28 图（1.8），该点表示具有这种速 率的分子所占的分数最大，这个最高点所对应的速率称之为最概然速率(vm) 解得 或 式中 M 为气体的摩尔质量。由此可见，最概然速率与质量的平方根成反比。在相同的温度 下，摩尔质量小的分子，其最概然速率大 P28 图（1.8） 。 2、分子的数学平均速率(va):所有分子速率的数学平均值。 3、根均方速率(u)： dN Nd dN Nf d ( )    =    或 22 书P (1.20) 1.5 2 4 2 ( ) exp 2 2 m m f kT kT         − =         1.5 2 4 2 exp 2 2 dN m m d N kT kT          − =         2 b m k T m  = 2 m RT M  = 8 a kT m   =

所有粒子的速率的平方值，除以粒子数N得到速率平方的平均值，然后再开方，称 为根均方速率。 B3kT μ=m 4、三种速率之比 2k互77=1：1128：124 :v.4=m VmV m 在三者中，最概然速率最小，根均方速率最大，数学平均速率居中。 在计算分子运动的平均距离时要用数学平均速率，而在计算平均平动能时要用根均方 速率。 1.5分子平动能的分布 上节介绍了分子运动速率的分布公式 dN= 4(m)} 由此很容易导出能量的分布公式： 各分子的能量 E=Im 所以 dE=mxdv 代入速率分布公式，则得 dNEN是分子能量处于E~E+E之间的分子占总分子中的分数，将式中dE前的系数写作 (E): 「E)称为能量分布函数。 如以能量分布函数E)为纵坐标，为横坐标作图，得图P32(图1.10) 此图与速率的分布（图P28图 1.8有大体相似之处。整个曲线下面的面积等于1，曲线下任 一区间的面积，代表能量落在该区间的分子占总分子数中的分数。不同的是：()曲线在开始 时较陡，升高很快，而速率分布曲线在起始时接近于水平。 (2)能量分布曲线通过最高点后，迅速降低（即比速率分布曲线降低得快）。 若设NE1©是能量超过E1的分子数，如果E1》kT 上式是三度空间中的公式。(P321.49) 8

8 所有粒子的速率的平方值，除以粒子数 N 得到速率平方的平均值，然后再开方，称 为根均方速率。 4、三种速率之比 在三者中，最概然速率最小，根均方速率最大，数学平均速率居中。 在计算分子运动的平均距离时要用数学平均速率，而在计算平均平动能时要用根均方 速率。 1.5 分子平动能的分布 上节介绍了分子运动速率的分布公式 由此很容易导出能量的分布公式: 各分子的能量 所以 代入速率分布公式，则得 dNE/N 是分子能量处于 E~(E+dE)之间的分子占总分子中的分数，将式中 dE 前的系数写作 f(E): 令 f(E)称为能量分布函数。 如以能量分布函数 f(E)为纵坐标，E 为横坐标作图，得图 P32(图 1.10) 此图与速率的分布(图 P28 图 1.8)有大体相似之处。整个曲线下面的面积等于 1。曲线下任 一区间的面积，代表能量落在该区间的分子占总分子数中的分数。不同的是:(1)曲线在开始 时较陡，升高很快，而速率分布曲线在起始时接近于水平。 (2)能量分布曲线通过最高点后，迅速降低(即比速率分布曲线降低得快)。 若设 NE1￫∞ 是能量超过 E1 的分子数，如果 E1》kT 上式是三度空间中的公式。（P32 1.49） 3kT m  = 2 8 3 : : : : 1:1.128:1.224 b m a k T kT kT m m m     = = 1.5 2 4 2 exp 2 2 dN m m d N kT kT          − =         1 2 2 E m =  dE m d =   1.5 1 2 2 1 exp E dN E E dE N kT kT      − =         1.5 1 2 2 1 ( ) exp E f E E  kT kT     − =         1 2 1 1 1 2 exp NE E E N kT kT  →     − =        

通常在物理化学中，只需要能量分布的近似公式，故从二度空间的速率分布公式导出相应 的能量分布公式，其结果为：推导过程在P33) 同理可得： Ns=ep-B-E）-指 N 代表能量超过E2与能量超过E1的分子数的比值。 1.6气体分子在重力场中的分布 通常我们所考虑的容器一般不是很大，总认为气体在容器中是均匀分布的，密度也不 随高度而变化，且各处的压力一样。 实际上，严格地讲在重力作用下，容器中上下层各处的密度并不完全一样，只不过差 别极其微小，可以忽略不计要了。如果高度差别较大，这种差别就不能忽略。 在重力场中，气体分子受到两种互相相反的作用。 (1无规则热运动将使气体分 子均匀分布 于它们所能达到的空间 (②)重力的作用则要使重的分子向下聚集。 由于这两种相反的作用，达到平衡时，气体分子在空间中并非均匀的分布，密度随高 度的增加而减少。 设在高度为h处的压力为P,高度h+dh处的压力为p-dp,两层的压力差为dp=pgdh P34图1.12气体随不同高度的分布 假定气体符合理想气体公式则。=MPRT 代入上式后得 dP Mg dh 对上式积分 人 假定在0一h的高度范围内温度不变，得 密 Po

9 通常在物理化学中，只需要能量分布的近似公式，故从二度空间的速率分布公式导出相应 的能量分布公式，其结果为：(推导过程在 P33) 同理可得： 代表能量超过 E2 与能量超过 E1 的分子数的比值。 1.6 气体分子在重力场中的分布 通常我们所考虑的容器一般不是很大，总认为气体在容器中是均匀分布的，密度也不 随高度而变化，且各处的压力一样。 实际上，严格地讲在重力作用下，容器中上下层各处的密度并不完全一样，只不过差 别极其微小，可以忽略不计罢了。如果高度差别较大，这种差别就不能忽略。 在重力场中，气体分子受到两种互相相反的作用。 (1)无规则热运动将使气体分子均匀分布于它们所能达到的空间 (2) 重力的作用则要使重的分子向下聚集。 由于这两种相反的作用，达到平衡时，气体分子在空间中并非均匀的分布，密度随高 度的增加而减少。 设在高度为 h 处的压力为 P,高度 h+dh 处的压力为 p-dp,两层的压力差为 dp=-ρgdh P34 图 1.12 气体随不同高度的分布 假定气体符合理想气体公式 则ρ= MP/RT 代入上式后得 对上式积分 假定在 0—h 的高度范围内温度不变，得 1 1 exp NE E N kT →   − =     2 2 1 1 exp E E kT E N E E N kT  − → →   − = − =     2 1 E E N N → → dP Mg dh P RT − = 0 0 p h p dp Mgdh p RT − =   0 ln p Mgh p RT = −

(1.52) 在即温数下，来精气体的省度女年华位体积内该气体的分子数成正出，与压力电威正 p n p Po no Po 式(1.52)可写为 p=Aen等) ”=等) 式(L.52八、式(L.53均称为Boltzmann(玻耳兹曼)公式。它指出了分子在重力场的分布规律， 指出压力、密度、单位体积中的分子数与高度的关系。 利用上述几个公式，可以近似地估计在不同高度处的大气压，或者反过来根据压力来计算 高度。但由于在上述公式的积分过程中，均将温度看作常数，所以只在高度相差不太大的 范围内，计算结果才与实际情况符合。 例题 已知某山区，其地面的大气压力1.013x105Pa,山顶的大气压力为.98X104P,设若 近似地认为山上和山下的温度不变，都是300K。请计算山项的高度（设空气在此高度花围内 组成不变，其摩尔质量为28.9X10-3 kg mol-1)。 解：根据式(152) Po RT 1.7分子的碰撞频率与平均自由程 一、分子的平均自由程 分子以很高的谏度做无规则云动，它们彼此不断地相互影撞 在分子的每两次连续碰撞之间所经过的略程叫做自由程，用L表示。自由程也是在不 断地无规则地改变着，其平均值叫做平均自由程 当一个分子趋向另一个分子，当它们之间的距离小到某一程度，斥力变得很大，分子 就要改变原来的方向而相互远离。这就完成了一次碰撞过程。 两个分子的质心碰撞时所能达到的最短距离称为有效直径或称为碰撞直径)。 设单位时间内 个分 子的平均速度为,在单位时间内与其他分子相碰的次数为，显然 i=U 在一群分子里（单位体积的分子数设为），假定只有一个分子移动，其他分子静止不动，移动 着的分子在单位时间内与其他分子相碰的次数（亿）为 02 (1.55) 实际上每个分子都是移动的，应该用相对速率()来代替上式中的平均速率， 相对速率：如果两个分子的运动方向是一致的，P37图1.15则V灯=0：如果两个分子的运动 方向是相反的，则Vr=2Va；若平均说来，分子以9的角度互相碰撞，每一个分子的速 率在两个分子质心连线上的分量为： 0

10 (1.52) 在同一温度下，某种气体的密度与每单位体积内该种气体的分子数成正比，与压力也成正 比，即 式(1.52)可写为 (1.53) 式(1.52)、式(1.53)均称为 Boltzmann(玻耳兹曼)公式。它指出了分子在重力场的分布规律， 指出压力、密度、单位体积中的分子数与高度的关系。 利用上述几个公式，可以近似地估计在不同高度处的大气压，或者反过来根据压力来计算 高度。但由于在上述公式的积分过程中，均将温度看作常数，所以只在高度相差不太大的 范围内，计算结果才与实际情况符合。 例题： 已知某山区，其地面的大气压力 1.013Х105Pa，山顶的大气压力为 7.98Х104Pa，设若 近似地认为山上和山下的温度不变，都是 300K。请计算山顶的高度(设空气在此高度范围内 组成不变，其摩尔质量为 28.9 Х10-3kg mol-1)。 解：根据式(1.52) 1.7 分子的碰撞频率与平均自由程 一、分子的平均自由程 分子以很高的速度做无规则运动，它们彼此不断地相互碰撞。 在分子的每两次连续碰撞之间所经过的路程叫做自由程，用 L 表示。自由程也是在不 断地无规则地改变着，其平均值叫做平均自由程 当一个分子趋向另一个分子，当它们之间的距离小到某一程度，斥力变得很大，分子 就要改变原来的方向而相互远离。这就完成了一次碰撞过程。 两个分子的质心碰撞时所能达到的最短距离称为有效直径(或称为碰撞直径)。 设单位时间内一个分子的平均速度为 va，在单位时间内与其他分子相碰的次数为 z’，显然 在一群分子里(单位体积的分子数设为 n),假定只有一个分子移动，其他分子静止不动,移动 着的分子在单位时间内与其他分子相碰的次数(Z’)为 (1.55) 实际上每个分子都是移动的，应该用相对速率(Vr) 来代替上式中的平均速率。 相对速率:如果两个分子的运动方向是一致的，P37 图 1.15,则 Vr =0；如果两个分子的运动 方向是相反的，则 Vr =2 Va ；若平均说来，分子以 900的角度互相碰撞，每一个分子的速 率在两个分子质心连线上的分量为： 0 exp Mgh p p RT   = −    0 0 0 p n p n   = = 0 exp Mgh RT     = −    0 exp Mgh n n RT   = −    0 ln p Mgh p RT = − ' a l z  = ' 2 a z d n =  1 2 2 a