《高等数学B》课程教学大纲 一、课程基本信息 课程 课程 9388002 高等数学 编号 名称 学分/学时 8学分/128学时(4/64,4/64) 开课时间 第1学期(13周)、第2学期(16周) 课程性质 专业基础课 先修课程 高中数学 考核方式 考试(平时30%、期末考试70%) 课程基 课程负责人 本情况 教材: 《高等数学》上下册,同济大学数学系编,人民邮电出版社, 2016年。 参考书目: 教材及 ①《高等数学》(第七版),同济大学数学系编,高等教育出版社, 2004年: 参考书 ② 《高等数学》(第二版)上下册,华东师范大学数学系编,华东 师范大学出版社: ③《高等数学》上下册,上海交通大学数学系编,上海交通大学出 版社,2017年 《高等数学》是生命、化学、食品科学等理工类专业开设专业必修课。本课程讲授函 课程 数、极限与连续,一元函数微分学及其应,一元函数积分学及其应用,微分方程,多 简介 元函数微分学,多元函数积分学,无穷级数。本课程是进一步学习与高等数学有关的 后续课程打基础。 学习目标1:了解高等数学课程的地位与性质,系统掌握高等数学的基本概念、基本 理论和基本方法。 课程学习 学习目标2:培养学生分析问题、解决问题的能力。 目标 学习目标3:为进一步学习后续课程,打下坚实的基础
1 《高等数学 B》课程教学大纲 一、课程基本信息 课程 编号 9388002 课程 名称 高等数学 课 程 基 本 情 况 学分/学时 8 学分/128 学时(4/64,4/64) 开课时间 第 1 学期(13 周)、第 2 学期(16 周) 课程性质 专业基础课 先修课程 高中数学 考核方式 考 试(平时 30%、期末考试 70%) 课程负责人 教材及 参考书 教材:《高等数学》上下册,同济大学数学系编,人民邮电出版社, 2016 年。 参考书目: ① 《高等数学》(第七版),同济大学数学系编,高等教育出版社, 2004 年; ② 《高等数学》(第二版)上下册,华东师范大学数学系编,华东 师范大学出版社; ③ 《高等数学》上下册,上海交通大学数学系编,上海交通大学出 版社,2017 年 课 程 简 介 《高等数学》是生命、化学、食品科学等理工类专业开设专业必修课。本课程讲授函 数、极限与连续,一元函数微分学及其应,一元函数积分学及其应用,微分方程,多 元函数微分学,多元函数积分学,无穷级数。本课程是进一步学习与高等数学有关的 后续课程打基础。 课程学习 目标 学习目标 1:了解高等数学课程的地位与性质,系统掌握高等数学的基本概念、基本 理论和基本方法。 学习目标 2:培养学生分析问题、解决问题的能力。 学习目标 3:为进一步学习后续课程,打下坚实的基础

二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 了解本专业的发展概况及其在社会发展中的重要作用,了 解本学科中学教学领域的一些新研究成果和教学方法;掌握教 育学、心理学和数学教育的基本理论,熟悉中小学教学技能以 2.3知识整合 及教育法规;学习人类文明进步与文化发展的通识知识。具 课程学习目标1、2、3 有整合数学、教育技术、教育学、心理学及本学科的知识和教 育技术并进行知识与技能重构的能力。 具备良好的数学素养,深入理解高等数学并掌握的基本理 论和方法,并能获得较强的逻辑推理能力和抽象思维能力。初 2.4教学能力 步掌握高等数学的基本思想方法,具有分析问题、解决实际问 课程学习目标1、2、3 题等基本能力:具有较强的独立学习能力和创新思维方式,懂 得教育教学基本规律,掌握现代教育教学、心理学的基本理论。 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章函数、极限与连续(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握集合及其运算、邻域、基本初等函数及初等函数的基本概念:数列、函数极限的基本 概念、求极限的基本方法及极限的性质及其证明:两个重要极限的应用:无穷大与无穷小的基本 概念及其关系、无穷小阶的比较:函数的连续性及其性质。 2.教学内容 第1.1节:集合与函数 第1.2节:数列极限的定义与计算 第1.3节:函数极限的定义与计算 第1.4节:极限性质 第1.5节:两个重要极限 第1.6节:无穷小与无穷大
2 二、课程学习目标与毕业要求指标点的对应关系 专业毕业要求 专业毕业要求指标点 对应的课程学习目标 2.3 知识整合 课程学习目标 1、2、3 2.4 教学能力 高等数学 课程学习目标 1、2、3 三、课程各要素与课程学习目标的对应关系及达成度分析 (一)课程教学内容、教学目标、学时分配与课程学习目标的对应关系 第一章 函数、极限与连续(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握集合及其运算、邻域、基本初等函数及初等函数的基本概念;数列、函数极限的基本 概念、求极限的基本方法及极限的性质及其证明;两个重要极限的应用;无穷大与无穷小的基本 概念及其关系、无穷小阶的比较;函数的连续性及其性质。 2 . 教学内容 第 1.1 节:集合与函数 第 1.2 节:数列极限的定义与计算 第 1.3 节:函数极限的定义与计算 第 1.4 节:极限性质 第 1.5 节:两个重要极限 第 1.6 节:无穷小与无穷大

第1.7节:函数的连续性及其性质 3·重点:数列极限的概念及性质,函数极限的概念与性质,函数极限与数列极限的关系,极限 存在准则两个重要极限和闭区间上连续函数的性质 4.难点:难点是数列极限与函数极限的概念。 5.参考习题: 习题1-1:第1(4)、2、3、4题(3、5、6)、6(2、5-8)、9-11、14-15题 习题1-2:第2(2-10)、3题 习题1-3:第1(3、5、6、8-14)、2-4题 习题1-5:第13(1)题 习题1-6:第2-4题 习题1-7:第1-12题 6.学时:20学时 第二章一元函数微分学及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握导数的基本概念及基本求导公式:求导数、高阶导数的方法与技巧:掌握微分的基本 概念及微分的求法:掌握微分中值定理的内容、证明方法及其应用:熟练掌握函数单调性的判别 方法、求函数的单调区间与极值、凹凸区间与拐点,求函数的最值、曲率,并可以解决一些简单 的实际问题 2.教学内容 第2.1节:导数的概念及基本求导公式 第2.2节:导数的计算法则 第2.3节:微分的概念应用 第2.4节:微分中值定理及其应用 第2.6节:函数的性态与图形 第27节:微分学的实际应用 3.重点:导数的定义,函数的求导法则及函数的微分,微分中值定理,洛必达法则,函数的单调 性与凹凸性,函数的极值与最值; 4难点:复合函数的求导法则,反函数及参数方程求高阶导数微分中值定理及其应用,函数图形 的描绘。 5.参考习题: 习题2-1:第1、3、4、6、8-11题 习题2-2:第1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19题 3
3 第 1.7 节:函数的连续性及其性质 3 . 重点: 4 . 难点: 5 . 参考习题: 习题 1-1:第 1(4)、2、3、4 题(3、5、6)、6(2、5-8)、9-11、14-15 题 习题 1-2:第 2(2-10)、3 题 习题 1-3:第 1(3、5、6、8-14)、2-4 题 习题 1-5:第 1-3(1)题 习题 1-6:第 2-4 题 习题 1-7:第 1-12 题 6 . 学时:20 学时 第二章 一元函数微分学及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握导数的基本概念及基本求导公式;求导数、高阶导数的方法与技巧;掌握微分的基本 概念及微分的求法;掌握微分中值定理的内容、证明方法及其应用;熟练掌握函数单调性的判别 方法、求函数的单调区间与极值、凹凸区间与拐点,求函数的最值、曲率,并可以解决一些简单 的实际问题 2 . 教学内容 第 2.1 节:导数的概念及基本求导公式 第 2.2 节:导数的计算法则 第 2.3 节:微分的概念应用 第 2.4 节:微分中值定理及其应用 第 2.6 节:函数的性态与图形 第 2.7 节:微分学的实际应用 3.重点: 5 . 参考习题: 习题 2-1:第 1、3、4、6、8-11 题 习题 2-2:第 1、2、3(5、6、11、13-16)、4(14-18)、5(11-18)、6、7(7-10)、8-19 题

习题2-3:第1、5、6、8、9题 习题2-4:第1-10题 习题2-6:第1(4、7、8)、2-6、914题 习题2-7:第1-25题 章节测试题:全部 6.学时:24学时 第三章一元函数积分学及其应用(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握不定积分的概念与性质,求不定积分的方法与技巧,定积分概念与性质,微积分基本公 式,求定积分的方法与技巧,定积分的应用,反常定积的基本概念及计算。 2.教学内容 第3.1节:不定积分的概念与性质 第3.2节:不定积分的换元法与分部法 第3.4节:定积分的概念与性质 第3.5节:微积分基本定理 第3.6节:定积分的换元法与分部法 第3.7节:定积分的几何应用 第3.8节:反常积分 3.重点:不定积分的概念与性质,不定积分的换元法与分部积分法;定积分的概念与性质,微积 分基本公式,定积分的换元积分与分部积分法;定积分微元法的思想,定积分在几何学方面的应 用。 4难点:利用第二换元积分法求不定积分;利用换元法求定积分;掌握微元法的思想及微元法的 应用。 5.参考习题: 习题3-1:第2(11、13、14、18-26)、3-7题 习题3-2:第2、4-6题 习题3-4:第3、4、6题 习题3-5:第113题 习题3-6:第1-10题 习题3-7:第1-8题 习题3-8:第1-3题
4 习题 2-3:第 1、5、6、8、9 题 习题 2-4:第 1-10 题 习题 2-6:第 1(4、7、8)、2-6、9-14 题 习题 2-7:第 1-25 题 章节测试题:全部 6 . 学时:24 学时 第三章 一元函数积分学及其应用(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握 2 . 教学内容 第 3.1 节:不定积分的概念与性质 第 3.2 节:不定积分的换元法与分部法 第 3.4 节:定积分的概念与性质 第 3.5 节:微积分基本定理 第 3.6 节:定积分的换元法与分部法 第 3.7 节:定积分的几何应用 第 3.8 节:反常积分 3.重点: 5 . 参考习题: 习题 3-1:第 2(11、13、14、18-26)、3-7 题 习题 3-2:第 2、4-6 题 习题 3-4:第 3、4、6 题 习题 3-5:第 1-13 题 习题 3-6:第 1-10 题 习题 3-7:第 1-8 题 习题 3-8:第 1-3 题

章节测试题:第1-5题 6.学时:22学时 第四章微分方程(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握微分方程的基本概念,可分离变量的微分方程,齐次方程,一阶线性微分方程,可降阶 的二阶微分方程,线性微分方程解的结构,常系数齐次线性微分方程,常系数非齐次线性微分方 程。 2.教学内容 第4.1节:微分方程的概念 第4.2节:一阶微分方程 第4.3节:二阶微分方程 3.重点:一阶线性微分方程,高阶线性微分方程,常系数非齐次线性微分方程; 4.难点:可降阶的高阶微分方程,常系数非齐次线性微分方程中特解的求法。 5.参考习题: 习题4-1:第1、2、5-7题 习题4-2:第1-3、5-7题 习题4-3:第1、4-6、8-9题 章节测试题:1、2、4-6 6.学时:14学时 第六章多元函数微分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二元函数的概念、极限与连续,偏导数,全微分,多元复合函数的求导法则,隐函数的 求导公式,方向导数与梯度,多元函数的极值及其求法。 2.教学内容 第6.1节:多元函数的概念、极限与连续 第6.2节:多元函数的偏导数与全微分 第6.3节:复合求导、隐函数求导 第6.4节:多元函数微分学的应用(多元函数的极值) 3.重点:多元函数的偏导数,全微分,复合函数的求导法则,隐函数的求导公式,多元函数的 极值及其求法; 4.难点:复合函数的高阶导数求法,隐函数的求导,多元函数的极值及求法。 5.参考习题: 5
5 章节测试题:第 1-5 题 6 . 学时:22 学时 第四章 微分方程(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握 2 . 教学内容 第 4.1 节:微分方程的概念 第 4.2 节:一阶微分方程 第 4.3 节:二阶微分方程 3.重 5 . 参考习题: 习题 4-1:第 1、2、5-7 题 习题 4-2:第 1-3、5-7 题 习题 4-3:第 1、4-6、8-9 题 章节测试题:1、2、4-6 6 . 学时:14 学时 第六章 多元函数微分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握 2 . 教学内容 第 6.1 节:多元函数的概念、极限与连续 第 6.2 节:多元函数的偏导数与全微分 第 6.3 节:复合求导、隐函数求导 第 6.4 节:多元函数微分学的应用(多元函数的极值) 3. 5 . 参考习题:

习题6-1:第1-3题 习题6-2:第1-14题 习题6-3:第138题 习题6-4:第15-24题 章节测试题:1(1-5)、2、6、7 6.学时:22学时 第七章多元函数积分学(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握二重积分的概念与性质,二重积分的计算法及应用 2.教学内容 第7.1节:二重积分的概念、计算及应用 3.重点:二重积分的概念与性质,二重积分的计算及应用 4.难点:在极坐标系下计算二重积分 5.参考习题: 习题7-1:第131题 章节测试题:第1(1)、2、3、4题 6.学时:10学时 第八章无穷级数(可支撑课程学习目标1、2、3) 1.教学目的和要求 掌握常数项级数的概念和性质,常数项级数的审敛法,幂级数,函数展开成幂级数,函数的 幂级数展开式的应用。 2.教学内容 第81节:常数项级数的概念与性质 第82节:常数项级数的审敛准则 第83节:幂级数的收敛及函数的展开式 3.重点:常数项级数的审敛法,幂级数,函数展开成幂级数及其应用。 4难点:常数项级数的审敛法,幂级数求和,函数展开成幂级数 5.参考习题: 习题8-1:第1、5-10题 习题8-2:第1-13题 习题8-3:第1-7题 6
6 习题 6-1:第 1-3 题 习题 6-2:第 1-14 题 习题 6-3:第 1-38 题 习题 6-4:第 15-24 题 章节测试题:1(1-5)、2、6、7 6 . 学时:22 学时 第七章 多元函数积分学(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握 2 . 教学内容 第 7.1 节:二重积分的概念、计算及应用 3. 5 . 参考习题: 习题 7-1:第 1-31 题 章节测试题:第 1(1)、2、3、4 题 6 . 学时:10 学时 第八章 无穷级数(可支撑课程学习目标 1、2、3) 1 . 教学目的和要求 掌握 2 . 教学内容 第 8.1 节:常数项级数的概念与性质 第 8.2 节:常数项级数的审敛准则 第 8.3 节:幂级数的收敛及函数的展开式 3.重点: 5 . 参考习题: 习题 8-1:第 1、5-10 题 习题 8-2:第 1-13 题 习题 8-3:第 1-7 题

章节测试题:第1(1-5)、2、3(1-5)题 6.学时:16学时 (二) 《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标1 课程学习目标2 课程学习目标3 第1.1-1.7节 H M M 第2.1-2.4,2.6-2.7节 H H H 第3.1-3.2,3.4-3.8节 H H H 第4.1-4.3节 H L H 第6.1-6.4节 H H H 第7.1节 H 第8.1-8.3节 H L L (三)《高等数学》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 学习目标1:了解高等数学课程的地位与性 质,系统掌握高等数学的基本概念、基本解法 和基本理论。 1.根据《高等数学》课程的特点,采用板书授 课的方式进行教学。注重高等数学基本概念、 学习目标2:会利用高等数学解决某些实际问 基本方法和基本理论的详细讲解。 题。 学习目标3:为进一步学习与高等数学有关的 后续课程,打下坚实的基础。 2.在理论讲授中,注意渗透数学思想、方法和 学习目标2:会利用高等数学解决某些实际问 原理:注意培养学生解决实际问题的能力,培 题。 >
7 章节测试题:第 1(1-5)、2、3(1-5)题 6 . 学时:16 学时 (二)《高等数学》课程学习目标与教学内容达成度矩阵图 章节名称 课程学习目标 1 课程学习目标 2 课程学习目标 3 第 1.1-1.7 节 H M M 第 2.1-2.4,2.6-2.7 节 H H H 第 3.1-3.2,3.4-3.8 节 H H H 第 4.1-4.3 节 H L H 第 6.1-6.4 节 H H H 第 7.1 节 H H H 第 8.1-8.3 节 H L L (三)《高等数学》课程教学方法与课程学习目标的对应关系矩阵图 课程教学方法 可支撑的课程学习目标 1. 根据《高等数学》课程的特点,采用板书授 课的方式进行教学。注重高等数学基本概念、 基本方法和基本理论的详细讲解。 学习目标 1:了解高等数学课程的地位与性 质,系统掌握高等数学的基本概念、基本解法 和基本理论。 学习目标 2:会利用高等数学解决某些实际问 题。 学习目标 3:为进一步学习与高等数学有关的 后续课程,打下坚实的基础。 2.在理论讲授中,注意渗透数学思想、方法和 原理;注意培养学生解决实际问题的能力,培 学习目标 2:会利用高等数学解决某些实际问 题
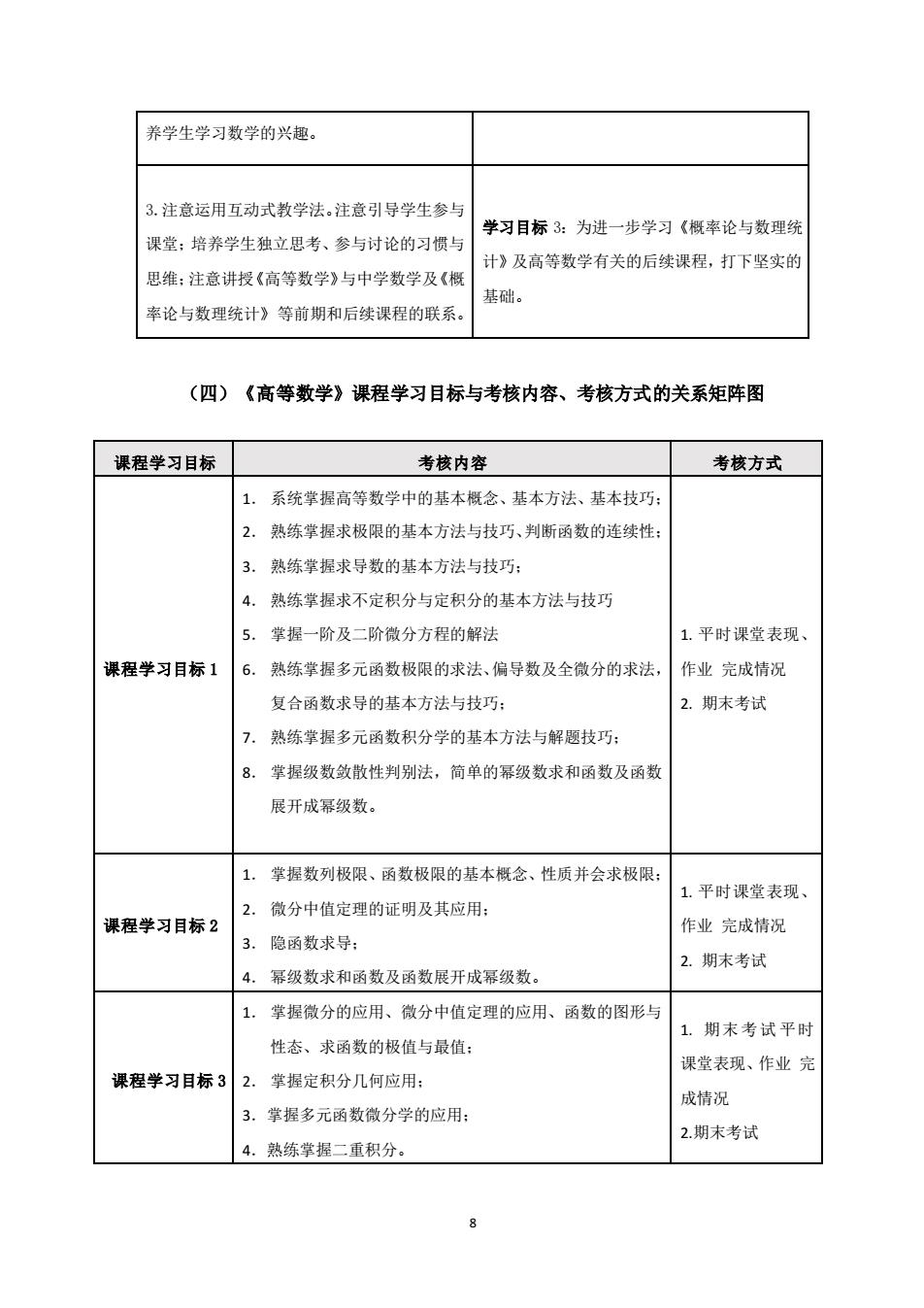
养学生学习数学的兴趣。 3.注意运用互动式教学法。注意引导学生参与 学习目标3:为进一步学习《概率论与数理统 课堂:培养学生独立思考、参与讨论的习惯与 计》及高等数学有关的后续课程,打下坚实的 思维:注意讲授《高等数学》与中学数学及《概 基础。 率论与数理统计》等前期和后续课程的联系。 (四)《高等数学》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 1. 系统掌握高等数学中的基本概念、基本方法、基本技巧: 2. 熟练掌握求极限的基本方法与技巧、判断函数的连续性: 3. 熟练掌握求导数的基本方法与技巧: 4. 熟练掌握求不定积分与定积分的基本方法与技巧 5. 掌握一阶及二阶微分方程的解法 1.平时课堂表现、 课程学习目标1 6.熟练掌握多元函数极限的求法、偏导数及全微分的求法, 作业完成情况 复合函数求导的基本方法与技巧: 2.期末考试 7. 熟练掌握多元函数积分学的基本方法与解题技巧: 8. 掌握级数敛散性判别法,简单的幂级数求和函数及函数 展开成幂级数。 1. 掌握数列极限、函数极限的基本概念、性质并会求极限: 1.平时课堂表现、 2.微分中值定理的证明及其应用: 课程学习目标2 作业完成情况 3. 隐函数求导: 2.期末考试 4. 幂级数求和函数及函数展开成幂级数。 1. 掌握微分的应用、微分中值定理的应用、函数的图形与 1.期末考试平时 性态、求函数的极值与最值: 课堂表现、作业完 课程学习目标3 2. 掌握定积分几何应用: 成情况 3.掌握多元函数微分学的应用: 2.期末考试 4. 熟练掌握二重积分
8 养学生学习数学的兴趣。 3.注意运用互动式教学法。注意引导学生参与 课堂;培养学生独立思考、参与讨论的习惯与 思维;注意讲授《高等数学》与中学数学及《概 率论与数理统计》等前期和后续课程的联系。 学习目标 3:为进一步学习《概率论与数理统 计》及高等数学有关的后续课程,打下坚实的 基础。 (四)《高等数学》课程学习目标与考核内容、考核方式的关系矩阵图 课程学习目标 考核内容 考核方式 课程学习目标 1 1. 系统掌握高等数学中的基本概念、基本方法、基本技巧; 2. 熟练掌握求极限的基本方法与技巧、判断函数的连续性; 3. 熟练掌握求导数的基本方法与技巧; 4. 熟练掌握求不定积分与定积分的基本方法与技巧 5. 掌握一阶及二阶微分方程的解法 6. 熟练掌握多元函数极限的求法、偏导数及全微分的求法, 复合函数求导的基本方法与技巧; 7. 熟练掌握多元函数积分学的基本方法与解题技巧; 8. 掌握级数敛散性判别法,简单的幂级数求和函数及函数 展开成幂级数。 1. 平时课堂表现、 作业 完成情况 2. 期末考试 课程学习目标 2 1. 掌握数列极限、函数极限的基本概念、性质并会求极限; 2. 微分中值定理的证明及其应用; 3. 隐函数求导; 4. 幂级数求和函数及函数展开成幂级数。 1. 平时课堂表现、 作业 完成情况 2. 期末考试 课程学习目标 3 1. 掌握微分的应用、微分中值定理的应用、函数的图形与 性态、求函数的极值与最值; 2. 掌握定积分几何应用; 3.掌握多元函数微分学的应用; 4.熟练掌握二重积分。 1. 期末考试 平时 课堂表现、作业 完 成情况 2.期末考试

(五)课程考核方法 1.平时课堂表现、作业完成情况(30%) 2.期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课题表现、作业完成情况(30%)、期末考试(闭卷,70%) 课程学习目标 期末考试(闭 课程分目标达成评价方法 成绩评定方法 卷) 课程学习目标1 约60% 课程学习目标2 约15% 分目标达成度=0.3×(平时课题表现、作业完成情况) 课程学习目标3 约25% +0.7×(期末考试) 合计 100 (七)课程学习目标与评分标准的对应关系 评分标准 课程学习目标 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 1.系统掌握高等数学中 1.掌握高等数学中 1.基本掌握高等数 对于高等数学的基 的基本概念、基本方法、 的基本概念、基本方 学中的基本概念、基 本概念、基本方法、 基本技巧: 法、基本技巧: 本方法、基本技巧: 基本理论,掌握比较 2.熟练掌握求极限的基 2.掌握求极限的基 2.会求数列和函数 欠缺。 本方法与技巧、判断函 本方法与技巧、判断 极限、判断函数的连 数的连续性: 函数的连续性: 续性: 3.熟练掌握求导数的基 3.掌握求函数的导 3.基本掌握求导数 课程学习目标1 本方法与技巧: 数的基本方法与技 的基本方法: 4.熟练掌握求不定积分 巧: 4.基本掌握求不定 与定积分的基本方法与 4.掌握求不定积分 积分与定积分的基 技巧: 与定积分的基本方 本方法: 5.熟练掌握一阶及二阶 法与技巧: 5.基本掌握一、二阶 微分方程的解法 5.掌握一阶及二阶 微分方程的解法 6.熟练掌握多元函数极 微分方程的解法 6.基本掌握多元函 9
9 (五)课程考核方法 1. 平时课堂表现、作业完成情况 (30%) 2. 期末考试(闭卷,70%) (六)课程成绩评定方法及其与课程学习目标的关系 平时课题表现、作业完成情况(30%)、期末考试(闭卷,70%) (七)课程学习目标与评分标准的对应关系 课程学习目标 评分标准 90-100 80-89 60-79 0-59 优 良 中/及格 不及格 课程学习目标1 1.系统掌握高等数学中 的基本概念、基本方法、 基本技巧; 2.熟练掌握求极限的基 本方法与技巧、判断函 数的连续性; 3.熟练掌握求导数的基 本方法与技巧; 4.熟练掌握求不定积分 与定积分的基本方法与 技巧; 5.熟练掌握一阶及二阶 微分方程的解法 6.熟练掌握多元函数极 1. 掌握高等数学中 的基本概念、基本方 法、基本技巧; 2. 掌握求极限的基 本方法与技巧、判断 函数的连续性; 3. 掌握求函数的导 数的基本方法与技 巧; 4. 掌握求不定积分 与定积分的基本方 法与技巧; 5. 掌握一阶及二阶 微分方程的解法 1. 基本掌握高等数 学中的基本概念、基 本方法、基本技巧; 2. 会求数列和函数 极限、判断函数的连 续性; 3. 基本掌握求导数 的基本方法; 4. 基本掌握求不定 积分与定积分的基 本方法; 5.基本掌握一、二阶 微分方程的解法 6. 基本掌握多元函 对于高等数学的基 本概念、基本方法、 基本理论,掌握比较 欠缺。 课程学习目标 成绩评定方法 期末考试(闭 卷) 课程分目标达成评价方法 课程学习目标 1 约 60% 分目标达成度=0.3×(平时课题表现、作业完成情况) +0.7×(期末考试) 课程学习目标 2 约 15% 课程学习目标 3 约 25% 合计 100
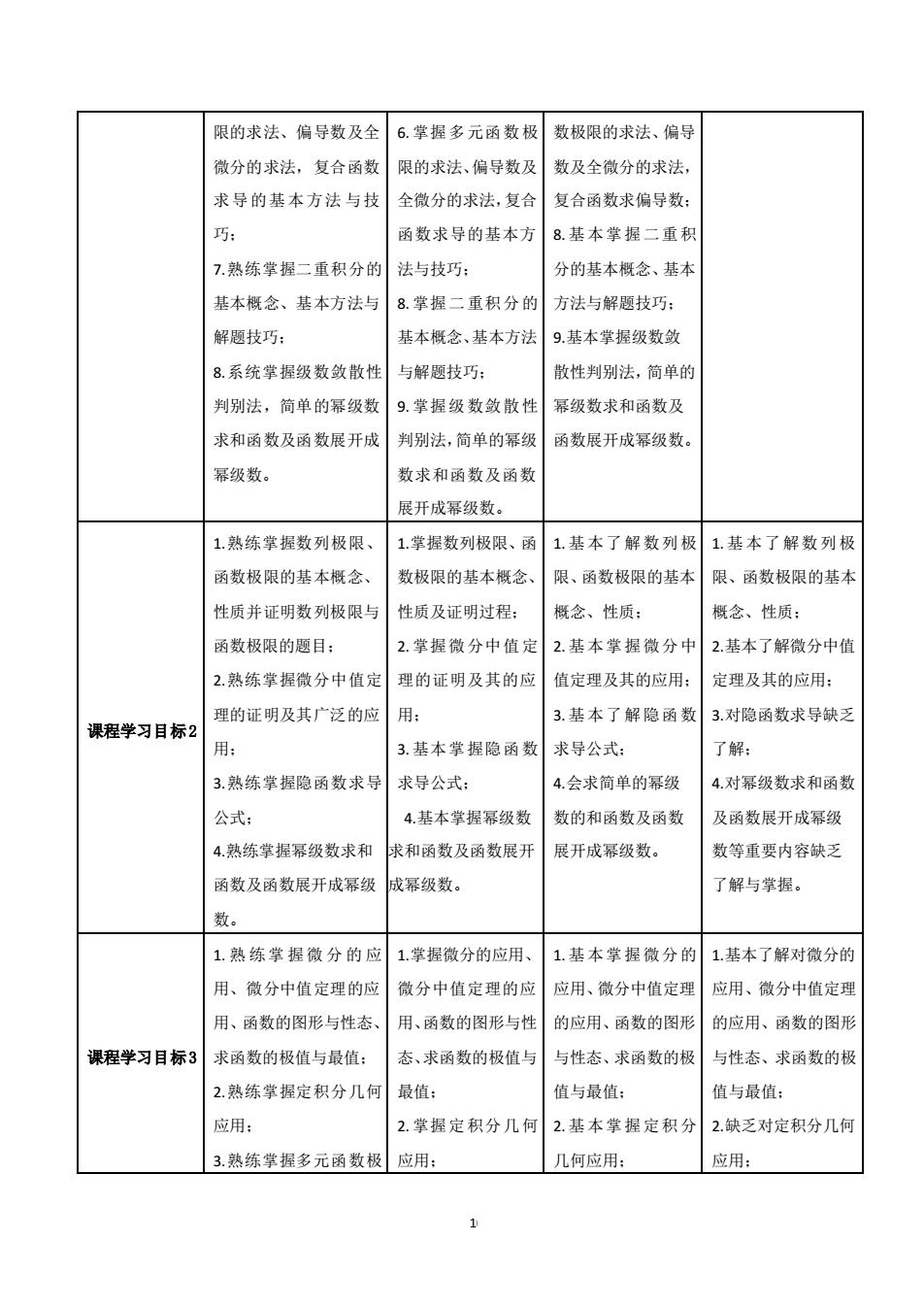
限的求法、偏导数及全 6.掌握多元函数极 数极限的求法、偏导 微分的求法,复合函数 限的求法、偏导数及 数及全微分的求法, 求导的基本方法与技 全微分的求法,复合 复合函数求偏导数: 巧: 函数求导的基本方 8.基本掌握二重积 7.熟练掌握二重积分的 法与技巧: 分的基本概念、基本 基本概念、基本方法与 8.掌握二重积分的 方法与解题技巧: 解题技巧: 基本概念、基本方法 9.基本掌握级数敛 8.系统掌握级数敛散性 与解题技巧: 散性判别法,简单的 判别法,简单的幂级数 9.掌握级数敛散性 幂级数求和函数及 求和函数及函数展开成 判别法,简单的幂级 函数展开成幂级数。 幂级数。 数求和函数及函数 展开成幂级数。 1.熟练掌握数列极限、 1.掌握数列极限、函 1.基本了解数列极 1.基本了解数列极 函数极限的基本概念、 数极限的基本概念、 限、函数极限的基本 限、函数极限的基本 性质并证明数列极限与 性质及证明过程: 概念、性质: 概念、性质: 函数极限的题目: 2.掌握微分中值定 2.基本掌握微分中 2.基本了解微分中值 2.熟练掌握微分中值定 理的证明及其的应 值定理及其的应用: 定理及其的应用: 理的证明及其广泛的应 用: 3.基本了解隐函数 3.对隐函数求导缺乏 课程学习目标2 用: 3.基本掌握隐函数 求导公式: 了解: 3.熟练掌握隐函数求导 求导公式: 4.会求简单的幂级 4.对幂级数求和函数 公式: 4.基本掌握幂级数 数的和函数及函数 及函数展开成幂级 4.熟练掌握幂级数求和 求和函数及函数展开 展开成幂级数。 数等重要内容缺乏 函数及函数展开成幂级 成幂级数。 了解与掌握。 数。 1.熟练掌握微分的应 1.掌握微分的应用、 1.基本掌握微分的 1.基本了解对微分的 用、微分中值定理的应 微分中值定理的应 应用、微分中值定理 应用、微分中值定理 用、函数的图形与性态、 用、函数的图形与性 的应用、函数的图形 的应用、函数的图形 课程学习目标3 求函数的极值与最值: 态、求函数的极值与 与性态、求函数的极 与性态、求函数的极 2.熟练掌握定积分几何 最值: 值与最值: 值与最值: 应用: 2.掌握定积分几何 2.基本掌握定积分 2.缺乏对定积分几何 3.熟练掌握多元函数极 应用: 几何应用: 应用:
10 限的求法、偏导数及全 微分的求法,复合函数 求导的基本方法 与技 巧; 7.熟练掌握二重积分的 基本概念、基本方法与 解题技巧; 8.系统掌握级数敛散性 判别法,简单的幂级数 求和函数及函数展开成 幂级数。 6. 掌握多元函数极 限的求法、偏导数及 全微分的求法,复合 函数求导的基本方 法与技巧; 8. 掌握二重积分的 基本概念、基本方法 与解题技巧; 9. 掌握级数敛散性 判别法,简单的幂级 数求和函数及函数 展开成幂级数。 数极限的求法、偏导 数及全微分的求法, 复合函数求偏导数; 8. 基本掌握二重积 分的基本概念、基本 方法与解题技巧; 9.基本掌握级数敛 散性判别法,简单的 幂级数求和函数及 函数展开成幂级数。 课程学习目标2 1.熟练掌握数列极限、 函数极限的基本概念、 性质并证明数列极限与 函数极限的题目; 2.熟练掌握微分中值定 理的证明及其广泛的应 用; 3.熟练掌握隐函数求导 公式; 4.熟练掌握幂级数求和 函数及函数展开成幂级 数。 1.掌握数列极限、函 数极限的基本概念、 性质及证明过程; 2. 掌握微分中值定 理的证明及其的应 用; 3. 基本掌握隐函数 求导公式; 4.基本掌握幂级数 求和函数及函数展开 成幂级数。 1. 基本了解数列极 限、函数极限的基本 概念、性质; 2. 基本掌握微分中 值定理及其的应用; 3. 基本了解隐函数 求导公式; 4.会求简单的幂级 数的和函数及函数 展开成幂级数。 1. 基本了解数列极 限、函数极限的基本 概念、性质; 2.基本了解微分中值 定理及其的应用; 3.对隐函数求导缺乏 了解; 4.对幂级数求和函数 及函数展开成幂级 数等重要内容缺乏 了解与掌握。 课程学习目标3 1. 熟 练掌 握微 分 的 应 用、微分中值定理的应 用、函数的图形与性态、 求函数的极值与最值; 2.熟练掌握定积分几何 应用; 3.熟练掌握多元函数极 1.掌握微分的应用、 微分中值定理的应 用、函数的图形与性 态、求函数的极值与 最值; 2. 掌握定积分几何 应用; 1. 基本掌握微分的 应用、微分中值定理 的应用、函数的图形 与性态、求函数的极 值与最值; 2. 基本掌握定积分 几何应用; 1.基本了解对微分的 应用、微分中值定理 的应用、函数的图形 与性态、求函数的极 值与最值; 2.缺乏对定积分几何 应用;