
MTSD@UPC 第二章 运动的量子理论 任浩 材料物理系 renh @upc.edu.cn 2022/3/24 材料化学系:结构化学 1
MTSD@UPC 第二章 运动的量子理论 任浩 材料物理系 renh@upc.edu.cn 2022/3/24 材料化学系:结构化学 1

MTSD@UPC ·分子的三种基本运动方式: ·平动 ·振动 。转动 ·用于存储能量 ·平动:如气体分子运动论 ·振动:如固体比热容 ·特殊的光谱学信号,用于表征微观结构 ·振动谱:红外、拉曼、中子散射、非弹性电子散射 ·电子一振动耦合 ·振动一转动谱 2022/3/24 材料化学系:结构化学 2
MTSD@UPC • 分子的三种基本运动方式: • 平动 • 振动 • 转动 • 用于存储能量 • 平动:如气体分子运动论 • 振动:如固体比热容 • 特殊的光谱学信号,用于表征微观结构 • 振动谱:红外、拉曼、中子散射、非弹性电子散射 • 电子—振动耦合 • 振动—转动谱 • …… 2022/3/24 材料化学系:结构化学 2

MTSD@UPC 第一节平动 平动(translation ·平动:物体在空间中位置的变动,注意与转动的 区别 ·Whittaker的定义: ·若物体从一个位置移动至另一个位置,且物体上每个 点初、末位置连线均互相平行,且长度为,(即物 体在空间中朝向不变),则此运动为平动,其方向平 行于这些连线,长度为。 ·最简单的运动方式,仍揭示了量子力学与经典力 学的不同,且有重要应用。 2022/3/24 材料化学系:结构化学 3
MTSD@UPC • 平动:物体在空间中位置的变动,注意与转动的 区别 • Whittaker的定义: • 若物体从一个位置移动至另一个位置,且物体上每个 点初、末位置连线均互相平行,且长度为𝑙,(即物 体在空间中朝向不变),则此运动为平动,其方向平 行于这些连线,长度为𝑙。 • 最简单的运动方式,仍揭示了量子力学与经典力 学的不同,且有重要应用。 2022/3/24 材料化学系:结构化学 3 第一节 平动 平动(translation)

MTSD@UPC 第一节平动 一维自由运动 ·一维空间中质量为m的自由粒子SEQ为 五2db(x) 2m dx2 =E() ·其通解为 (c)=Aei十Bei,E= 九22 2m ·A和B为常数,波函数和能量均依赖于k ·k可以连续取值:对任意飞,波函数满足约束条件 ·能量是k的函数,也可以取任意非负值 →自由粒子的平动能量不是量子化的 ·常数A和B的取值取决于运动状态: ·若粒子向正方向运动,卫=十k,则B=0,A为归一化常数 ·反之亦然 2022/3/24 材料化学系:结构化学 4
MTSD@UPC • 一维空间中质量为m的自由粒子SEQ为 • 其通解为 • A和B为常数,波函数和能量均依赖于𝑘 • 𝑘可以连续取值:对任意𝑘,波函数满足约束条件 • 能量是𝑘的函数,也可以取任意非负值 ➔自由粒子的平动能量不是量子化的 • 常数𝐴和𝐵的取值取决于运动状态: • 若粒子向正方向运动,𝑝 = +ℏ𝑘,则𝐵 = 0,𝐴为归一化常数 • 反之亦然 2022/3/24 材料化学系:结构化学 4 第一节 平动 一维自由运动
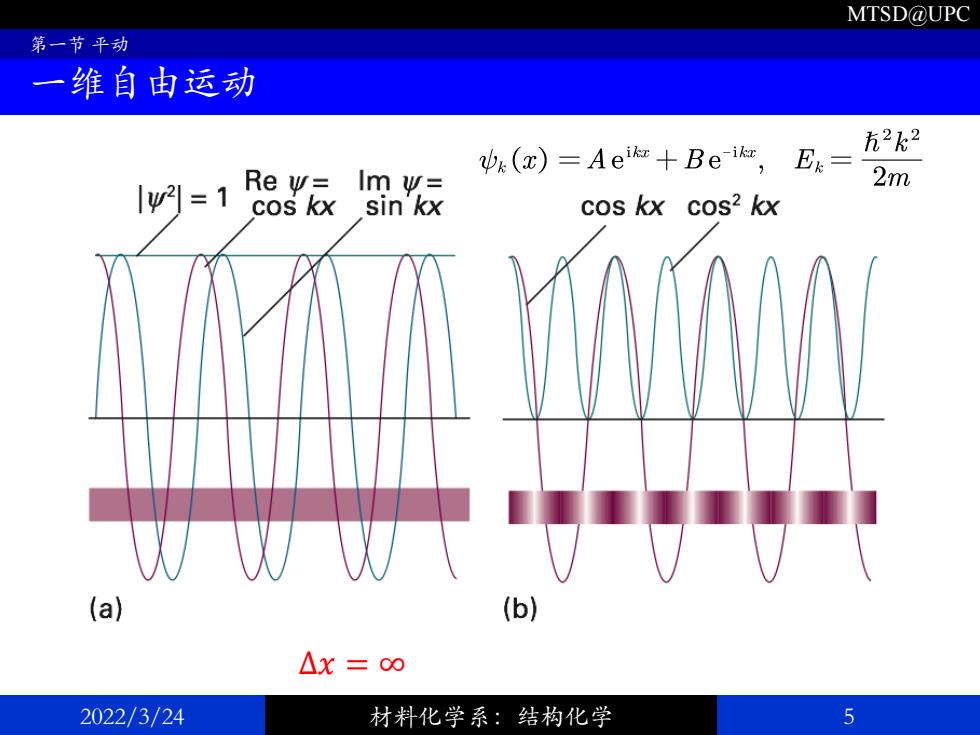
MTSD@UPC 第一节平动 一维自由运动 x (x)=Aeik+Be-ikr, 五2k2 Iw列=18san 2m cos kx cos2 kx (a) (b) △X=∞ 2022/3/24 材料化学系:结构化学 5
MTSD@UPC 2022/3/24 材料化学系:结构化学 5 第一节 平动 一维自由运动 例:使用加速器将一个电子由静止开始向+𝑥 方向加速,经过1.0 V电势加速后, 电子的动能为1.0 𝑒𝑉,或0.16 𝑎𝐽 (1.6 × 10−19 𝐽)。此时电子的波函数由上式给 出,其中B=0, 故波函数为 练习:若电子被10 kV加速器向负方向加速,写出其波函数。 Δ𝑥 = ∞

MTSD@UPC 第一节平动 一维约束体系:限制性运动 ·一维势箱 V(x)= 0, 0I ·在势箱内部,SEQ同自由粒子相同 ·具有相同通解 吵k(x)=Aei+Beik Location,x 验证与三角函数形式相同 ·势箱外部,由于势能为无穷大,波函数为零(粒子跑不到外面) 吵(x)=0,forxL ·与自由粒子波函数有何不同? 2022/3/24 材料化学系:结构化学 6
MTSD@UPC • 一维势箱 • 在势箱内部,SEQ同自由粒子相同 • 具有相同通解 • 势箱外部,由于势能为无穷大,波函数为零(粒子跑不到外面) • 与自由粒子波函数有何不同? 2022/3/24 材料化学系:结构化学 6 第一节 平动 一维约束体系:限制性运动 验证与三角函数形式相同

MTSD@UPC 第一节平动 一维约束体系:考虑波函数约束条件 ·已知波函数具有如下形式 (x)= ∫Aei+Bei, 0L ·波函数必须连续:引入边界条件 ψk(0)=0,andψk(L)=0 ·允许的波函数及能量具有如下形式: (0)=Csin m7πx n=1,2,… En= n2h2 验证 8mL2, n=1,2,… ·引入边界条件导致能量量子化:约束条件要求波函数具有特定形式, 从而限制了力学量(此处为能量)只能取离散值。 2022/3/24 材料化学系:结构化学 7
MTSD@UPC • 已知波函数具有如下形式 • 波函数必须连续:引入边界条件 • 允许的波函数及能量具有如下形式: • 引入边界条件导致能量量子化:约束条件要求波函数具有特定形式, 从而限制了力学量(此处为能量)只能取离散值。 2022/3/24 材料化学系:结构化学 7 第一节 平动 一维约束体系:考虑波函数约束条件 验证

MTSD@UPC 第一节平动 一维约束体系:归一化 波函数: (0)=Csin 27πc m=1,2,… 代入归一化条件: =c血() -c号-1 故有C=(2/L)12。则一维势箱中波函数的最终形式为: 1/2 0L 能级为: En= n2h2 8mL2, m=1,2,… 2022/3/24 材料化学系:结构化学 8
MTSD@UPC 波函数: 代入归一化条件: 故有 𝐶 = 2Τ𝐿 1/2。则一维势箱中波函数的最终形式为: 能级为: 2022/3/24 材料化学系:结构化学 8 第一节 平动 一维约束体系:归一化

MTSD@UPC 第一节平动 一维约束体系:讨论 2 1/2 v(x) 0L 赖于整数no ·一维势箱中,n=1,2, En= n2h2 8mL2, n=1,2,… ·波函数的个数无限 n 100 10 ·无限个能级 Classically allowed energies 81 9 ·能量随n增大而增加 8 ·能级差随n增大而增加 > 3 6 5 6 432 0 2022/3/24 材料化学系:结构化学 9
MTSD@UPC • 量子数:波函数和能级均依 赖于整数 𝑛。 • 一维势箱中,𝑛 = 1, 2, … • 波函数的个数无限 • 无限个能级 • 能量随𝑛增大而增加 • 能级差随𝑛增大而增加 2022/3/24 材料化学系:结构化学 9 第一节 平动 一维约束体系:讨论
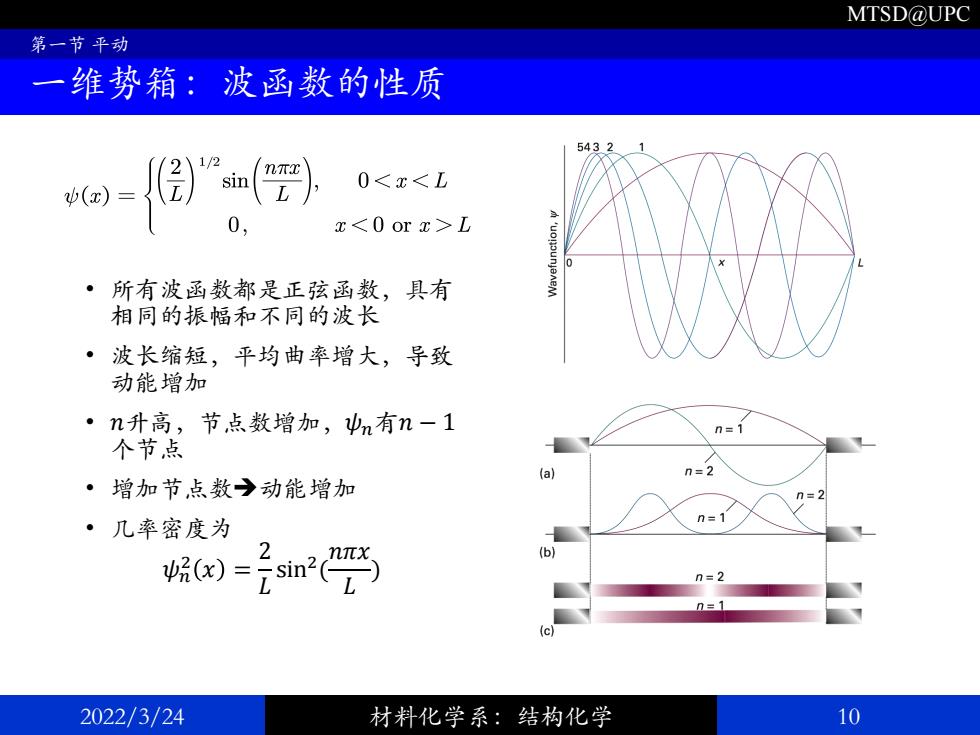
MTSD@UPC 第一节平动 一维势箱:波函数的性质 541 / v(x) sin(nmr) 0L ·所有波函数都是正弦函数,具有 相同的振幅和不同的波长 ·波长缩短,平均曲率增大,导致 动能增加 ·n升高,节点数增加,n有n-1 n三 个节点 a】 ·增加节点数→动能增加 n=2 ·几率密度为 呢6e=元sin2 2 6 n=2 2022/3/24 材料化学系:结构化学 10
MTSD@UPC • 所有波函数都是正弦函数,具有 相同的振幅和不同的波长 • 波长缩短,平均曲率增大,导致 动能增加 • 𝑛升高,节点数增加,𝜓𝑛有𝑛 − 1 个节点 • 增加节点数➔动能增加 • 几率密度为 𝜓𝑛 2 𝑥 = 2 𝐿 sin2 ( 𝑛𝜋𝑥 𝐿 ) 2022/3/24 材料化学系:结构化学 10 第一节 平动 一维势箱:波函数的性质