Introduction 1.对称性是物理体系、化学体系的普遍性质之一 对不同形式的体系,对称性具有不同的内涵 2.应用对称性原理可以建立体系状态性质与其特定对称 性质的关联,使问题的研究得以简化 Example1CH4电子结构 8个价电子分为两组:~14eV(6个电子);~23eV(2个电子) HΨ=EΨ Ta点群 月=-+ C CH, 4H =3 2a 2++↓ 对称化的MOs 2p+++ 十十+十 ↓ 2x1 扑扑扑Ps:V) 1.3 1.5 1.8 2.1 24 Ionization energy MJ.mol a.2 UrS:210) A0s(C:2s,2p,/2p,2p;4H:41s)
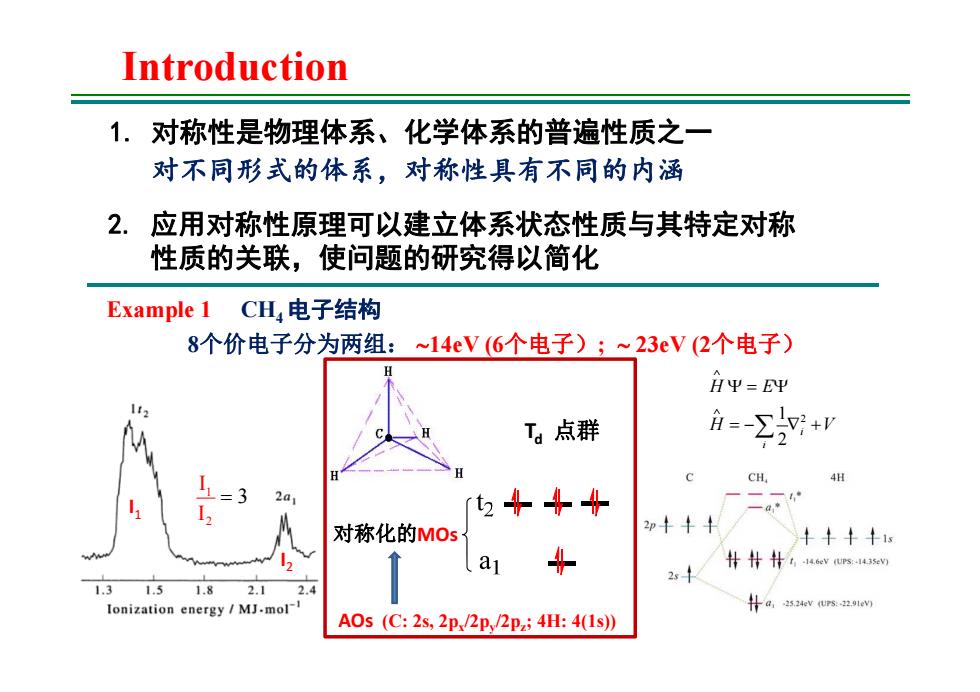
Introduction 1. 对称性是物理体系、化学体系的普遍性质之一 对不同形式的体系,对称性具有不同的内涵 2. 应用对称性原理可以建立体系状态性质与其特定对称 性质的关联,使问题的研究得以简化 Example 1 CH4 电子结构 8个价电子分为两组: 14eV (6个电子); 23eV (2个电子) I1 I2 1 2 I I 3 Td 点群 AOs (C: 2s, 2px/2py/2pz; 4H: 4(1s)) 对称化的MOs H V H E i i 2 2 1
Example2球对称场中Ym(e,中)的性质(形式) V(r)→球对称场 e(r06) dr=dx dy dz =r2sinedr dedo x'yizk x=rsinecos 1=i+j+ki方k为整数 y=rsinesino z=rcos0 对给定的,可能的次函数集合构成其不变 V=(Ze)e 的子空间 r i=j=1,k=0 ¥,dy i=k=1,j=0 ,d 1=0,i=j=k=0, 1,s jk=1,i=0 ,dz 1=2,i+j+k=2 r i=1,j=k=0 Px i=2,jk=0 j2,i=k=0 1=1,i+j+k=1- j1,ik=0¥,py Lk=2,i=j=0 k=1,ij=0,P2 x2-y ,z2 在球对称场中(原子体系) 3r2-2 5个d轨道是简并的 d
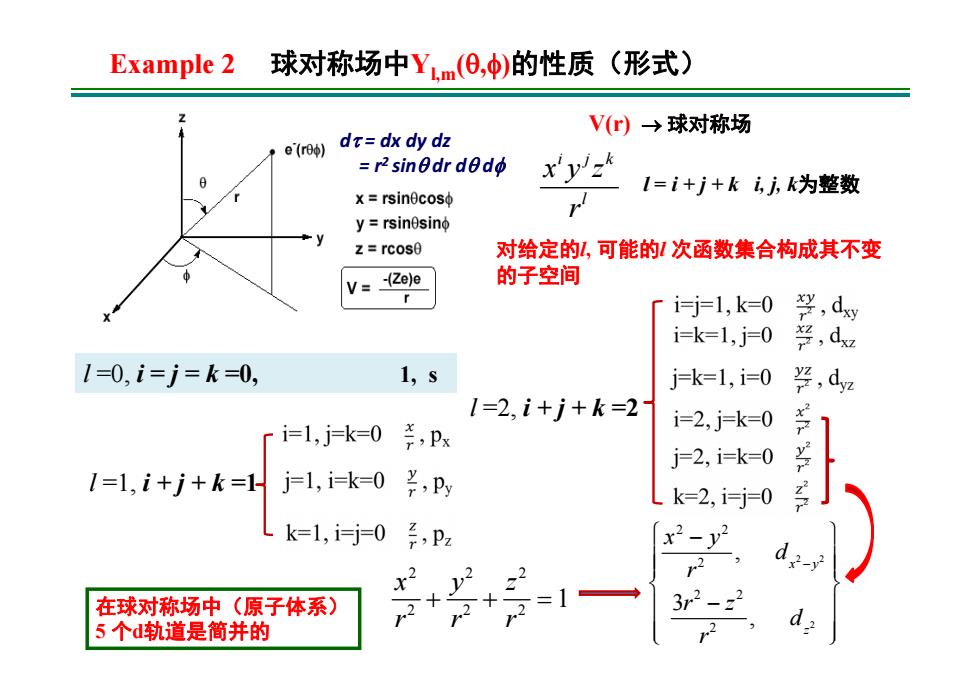
Example 2 球对称场中Yl,m(,)的性质(形式) i jk l x y z r V(r) 球对称场 l = i + j + k i, j, k为整数 对给定的l, 可能的l 次函数集合构成其不变 的子空间 l =1, i + j + k =1 l =0, i = j = k =0, 1, s l =2, i + j + k =2 2 22 222 1 xyz rrr 2 2 2 2 2 2 2 2 2 , 3 , x y z x y d r r z d r 在球对称场中(原子体系) 5 个d轨道是简并的 d = dx dy dz = r2 sin dr d d
低对称性下简并轨道能级的分裂 八面体场(0/0) 在八面体群操作下不变 dy de,d a-,d} 进一步降低对称性→C4轴拉长 C4X。→y C3消失,轨道分组: {dw,de,d}→{d,d} dy ad}-a月 {d} dy d 0& d ag 炉为 be 是的 g dd eg 0 Dab/Cab
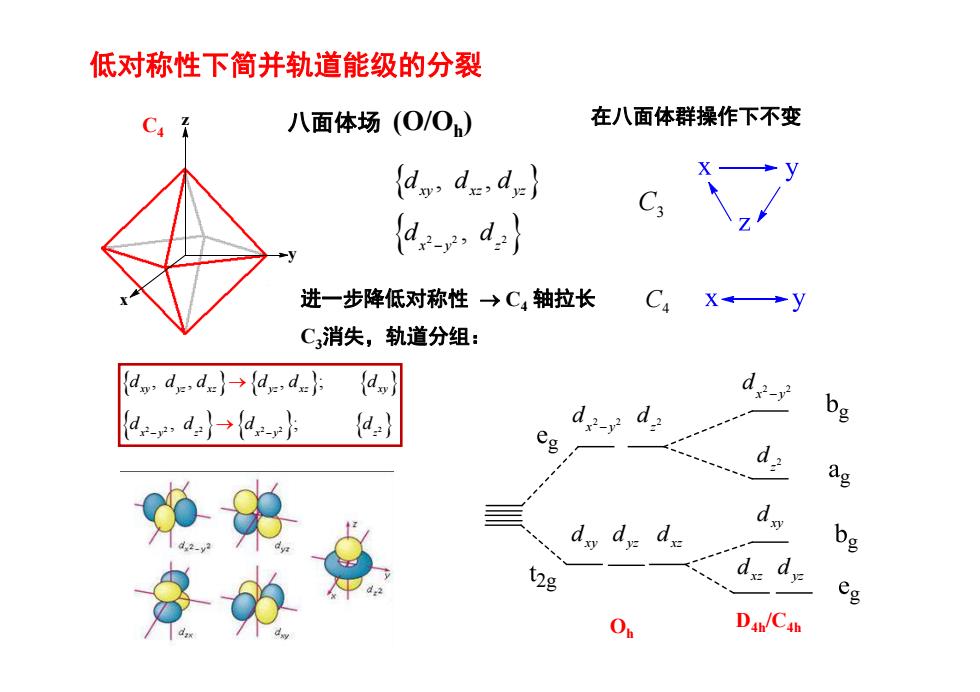
低对称性下简并轨道能级的分裂 22 2 , , , xy xz yz xy z d dd d d 进一步降低对称性 C 4 轴拉长 C 3消失,轨道分组: 八面体场 (O/O h ) C3 C4 x y C z 在八面体群操作下不变 4 22 2 22 2 , , , ; , ; xy yz xz yz xz xy xy z xy z d dd dd d dd d d g 2g g g g g 22 2 x y z d d xz yz d d 2 2 x y d 2z d xy d xy yz xz dd d O h D4h/C4h
dx2y2 big dz2 dx2-y2 eg t29 d22 a1g t2 6Dq d网p29 dxy 4Dq b2g -e dz2 dx2-y2 dz2 _a1g eg dyz dxz eg 立方体场 四面体场 球形场 八面体场四方畸变 平面四方场 Ou Ta On Dah Dah
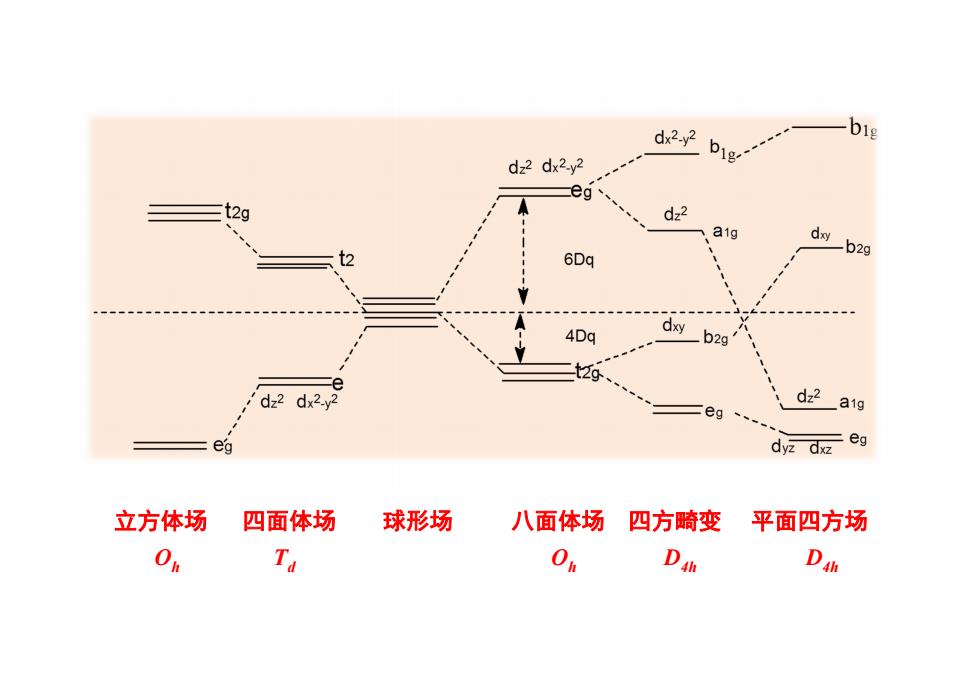
立方体场 四面体场 球形场 八面体场 四方畸变 平面四方场 O h Td O h D4h D4h
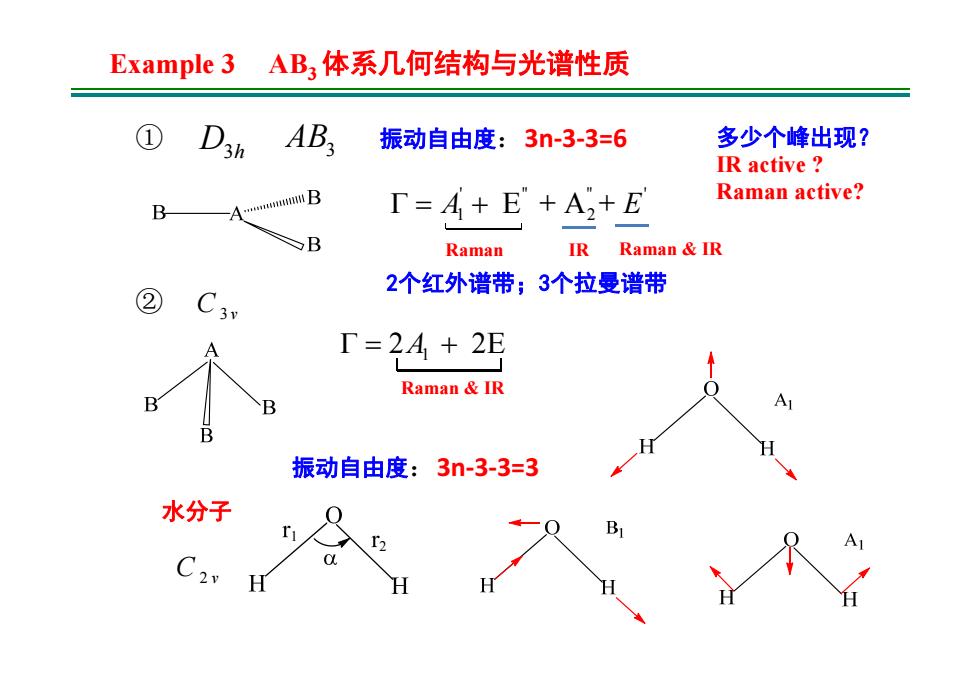
Example3AB,体系几何结构与光谱性质 ① D3h AB. 振动自由度:3n-3-3=6 多少个峰出现? IR active Raman active? B B T=4+E+A,+E ✉B Raman IR Raman IR 2个红外谱带;3个拉曼谱带 2 C3 Γ=2A+2E Raman IR 振动自由度:3n-3-3=3 水分子
多少个峰出现? IR active ? Raman active? C3 v ① AB3 ' " "' A1 2 E + A + E ② D3h 振动自由度:3n‐3‐3=6 Raman Example 3 AB3 体系几何结构与光谱性质 IR Raman & IR 2个红外谱带;3个拉曼谱带 1 2 2E A Raman & IR C 2 v 1 2 振动自由度:3n‐3‐3=3 水分子

内容简介 本课程包括四个部分的内容:群论基础、群表示理论、 分子对称群的不可约表示、光谱学和量子化学中的一 些群论问题。从群论的严格数学基础开始,以化学工 作者易接受的方式介绍群的定义、分子对称性、群表 示、分子对称群不可约表示特征标的构造等基础知识, 并以实例说明群论方法在量子化学计算、化学键理论、 化学反应性、分子光谱等化学领域中的应用
内容简介 本课程包括四个部分的内容:群论基础、群表示理论、 分子对称群的不可约表示、光谱学和量子化学中的一 些群论问题。从群论的严格数学基础开始,以化学工 作者易接受的方式介绍群的定义、分子对称性、群表 示、分子对称群不可约表示特征标的构造等基础知识, 并以实例说明群论方法在量子化学计算、化学键理论、 化学反应性、分子光谱等化学领域中的应用

主要参考文献 1.群论在化学中的应用,[美]F.A.Cotton著,刘春万等译,福 建科学技术出版社,第三版,1999 2.Group Theory and its Application to Physical Problems,M. Hamermesh,Dover Publications,Inc.New York,1989 3.群论及其在固体物理中的应用,徐婉棠,喀兴林编著,高等 教育出版社,1999 4.Group Theory and its Application to the Quantum Mechanics of Atomic Spectra,E.P.Wigner,Academic Press,1959. 5.群论,韩其智,孙洪洲,北京大学出版社,1988
主要参考文献 1. 群论在化学中的应用,[美] F. A. Cotton 著,刘春万等译,福 建科学技术出版社,第三版,1999 2. Group Theory and its Application to Physical Problems, M. Hamermesh, Dover Publications, Inc. New York, 1989 3. 群论及其在固体物理中的应用,徐婉棠,喀兴林 编著,高等 教育出版社,1999 4. Group Theory and its Application to the Quantum Mechanics of Atomic Spectra, E. P. Wigner, Academic Press, 1959. 5. 群论,韩其智,孙洪洲,北京大学出版社,1988