
第六章群论 6.1群论基础 1群的定义 设G是一些元素的集合,G={80,1,,}在G中定义了乘 法运算,如果G对这种运算满足下面四个条件: (I)有唯一的单位元e.e∈G,对任意feG,都有 ef=fe=f (2)封闭性.对任意f,g∈G,若fg=h必有h∈G (3)结合律.对任意f,g,h∈G,都有 (fg)h=f(gh) (4)逆元素.对任意f∈G,有唯一的f∈G,使 ff=ff=e, 则称G为一个群e称为群G的单位元,f称为f的逆元素。有限 群中群元素的数目称为群的阶。 2群的乘法表 二阶群 G2E A E EA AA E
第六章 群论 6.1 群论基础 1 群的定义 设 G 是一些元素的集合,G = {g0, g1, …, gi, …}. 在 G 中定义了乘 法运算,如果 G 对这种运算满足下面四个条件: (1) 有唯一的单位元 e. e ∈G, 对任意 f ∈G, 都有 ef = fe = f (2) 封闭性. 对任意 f , g∈G, 若 f g= h, 必有 h ∈G. (3) 结合律 . 对任意 f , g, h∈G, 都有 (f g) h = f (g h) (4) 逆元素. 对任意 f ∈G, 有唯一的 f -1 ∈G,使 f f -1= f -1f = e, 则称 G 为一个群. e 称为群 G 的单位元,f –1 称为 f 的逆元素。有限 群中群元素的数目称为群的阶。 2 群的乘法表 二阶群 G2 E A E E A A A E

三阶群 G3E A B EAB A ABE BB E A (①若AA=A2=E>BB=B2=E,>AB=B>A=E(不合理) (ii)AA=A2=B,AB=AA2=A3=E;BA=E,BB=A G3E A A2 E E A A2 A AA2E 一循环群 G={X,X2,X3,,X=E} 一Abel群AB=BA 四阶群 ()四阶循环群 X=A X2=B X3=C X=E G()E A B C EE A B C A A B C E BB C E A CC EA B
三阶群 G3 E A B E E A B A A B E B B E A (i) 若 AA = A2 = E -> BB = B2 = E; -> AB = B -> A = E(不合理) (ii) 若 AA = A2 = B, AB = AA2 = A3 = E; BA = E, BB = A. G3 E A A2 E E A A2 A A A2 E A2 A2 E A — 循环群 G = { X, X2 , X3 , …, Xn = E} — Abel 群 AB = BA. 四阶群 (i) 四阶循环群 X = A X2 = B X3 = C X4 = E G4 (1) E A B C E E A B C A A B C E B B C E A C C E A B

( G②EABC E EAB C A AECB B B Ex1构造五阶群的乘法表。 3子群 在G2中,子集:{E,A5;{E,B;{E,C}构成较小的群一一子 群。 定理:g阶群G的任意子群H,它的阶h必为g的除数。即, 8=hn,n为整数。 如:G6的子群的阶是:6和1,2,3。 4类 若A=XBX,称A和B共轭。若A和B及C共轭,则B与C 共轭。相互共轭的元素完整集合称为群的类。 所有类的阶必定是群阶的整数因子 Ex2把G3,G:四G,②,G群的元素整理成类
(ii) G4 (2) E A B C E E A B C A A E C B B B C E A C C B A E Ex1 构造五阶群的乘法表。 3 子群 在 G4 (2)中,子集:{E, A}; {E, B}; {E, C} 构成较小的群——子 群。 定理: g 阶群 G 的任意子群 H, 它的阶 h 必为 g 的除数。即, g =hn, n 为整数。 如:G6的子群的阶是:6 和 1,2,3。 4 类 若 A = X-1BX, 称 A 和 B 共轭。若 A 和 B 及 C 共轭,则 B 与 C 共轭。相互共轭的元素完整集合称为群的类。 所有类的阶必定是群阶的整数因子。 Ex 2 把 G3, G4 (1), G4 (2), G5群的元素整理成类
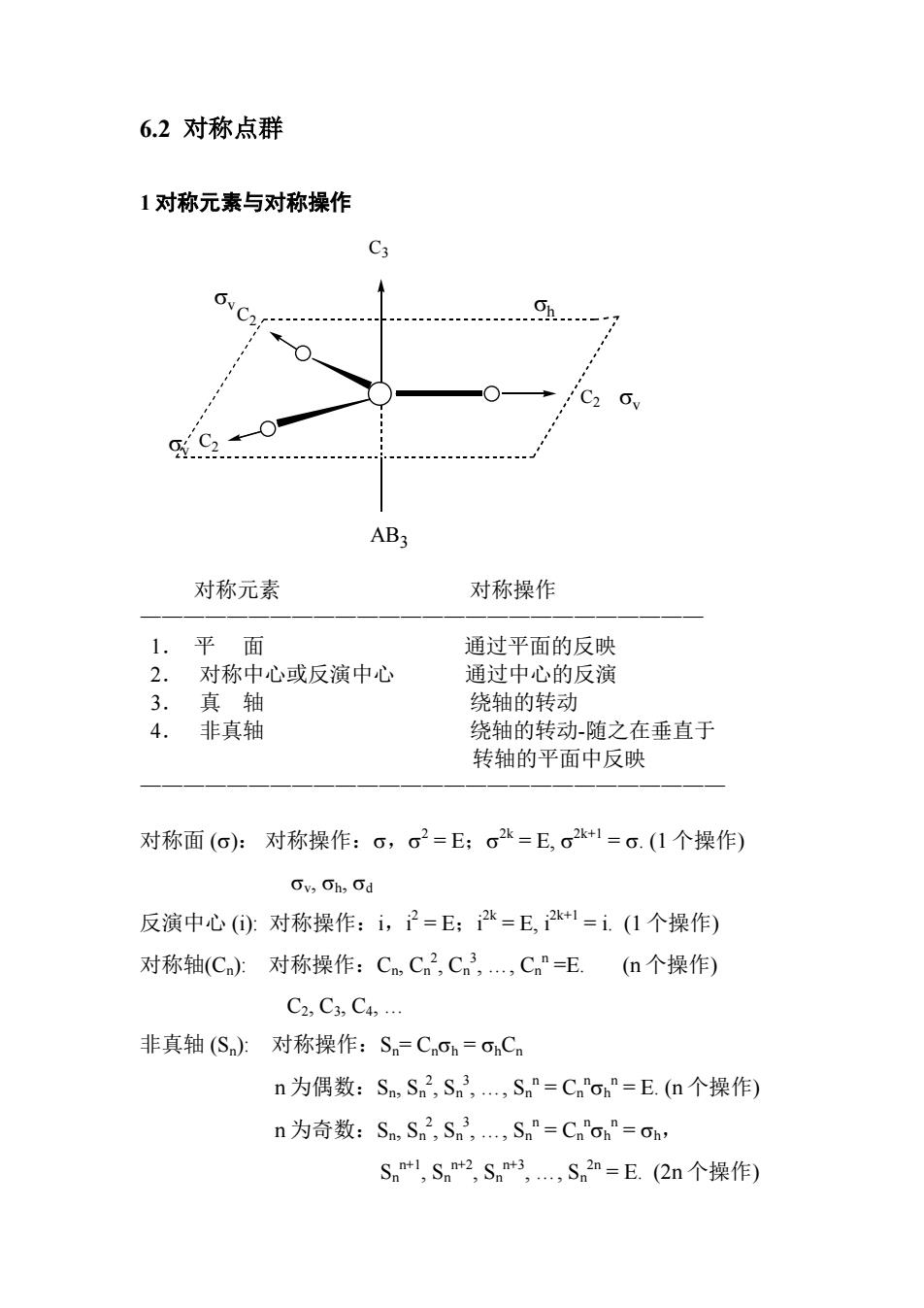
6.2对称点群 1对称元素与对称操作 C2 v AB3 对称元素 对称操作 1.平面 通过平面的反映 2 对称中心或反演中心 通过中心的反演 3. 真轴 绕轴的转动 非真轴 绕轴的转动-随之在垂直于 转轴的平面中反映 对称面(o):对称操作:6,σ2=E;o2k=E,。2k+1=。.(1个操作) Gv,Oh,Od 反演中心①):对称操作:i,子-E:=E,1=i(1个操作) 对称轴(C)对称操作:Cm,C2,Cn3,Cn=E.n个操作) C2,C,C4, 非真轴(S):对称操作:S。=Cnoh=oCn n为偶数:Sm,Sa2,Sn3,,Snn=Cmoh"=E.(n个操作) n为奇数:Sn,Sn2,Sn3,,Sm”=Cnoh"=oh, Sm,Snmt2,Sn*3,,Sn2n=E.(2n个操作)
6.2 对称点群 1 对称元素与对称操作 C3 C2 C2 C2 σv σv σv σh AB3 对称元素 对称操作 —————————————————————————— 1. 平 面 通过平面的反映 2. 对称中心或反演中心 通过中心的反演 3. 真 轴 绕轴的转动 4. 非真轴 绕轴的转动-随之在垂直于 转轴的平面中反映 ——————————————————————————— 对称面 (σ): 对称操作:σ,σ 2 = E;σ 2k = E, σ 2k+1 = σ. (1 个操作) σv, σh, σd 反演中心 (i): 对称操作:i,i 2 = E;i 2k = E, i2k+1 = i. (1 个操作) 对称轴(Cn): 对称操作:Cn, Cn 2 , Cn 3 , …, Cn n =E. (n 个操作) C2, C3, C4, … 非真轴 (Sn): 对称操作:Sn= Cnσh = σhCn n 为偶数:Sn, Sn 2 , Sn 3 , …, Sn n = Cn n σh n = E. (n 个操作) n 为奇数:Sn, Sn 2 , Sn 3 , …, Sn n = Cn n σh n = σh, Sn n+1, Sn n+2, Sn n+3, …, Sn 2n = E. (2n 个操作)

2等价对称元素 若一个对称元素A被一个操作变为元素B,这一操作是由第三个 元素X所生成的,当然可以用X把B变回A.A和B两个元素称为 等价. 例如:NH分子:对称元素:{C3,o,(I),o,(2),,(3)} 0(2) 51) (3) C3o(1)=o(2),C3C3o,(1)=C32o,(1)=o,(3) 所以,三个对称面等价。 3对称点群 分子点群:对称操作的完全集合构成的群一一对称点群。 例1:G={ov,o,2=E}FONO:Cs点群 单位元:E,封闭性.c,ov=o,2=E,oE=cv 逆元素.ov=ov 例2:G={E,C2,o,(1),o(2)}H20:C2v点群 单位元:E 封闭性.G(1)C2=C25(1)=G,(2),5(1)G,(2)=C 逆元素:C2=C2,Gv=o 结合律.{C2o,(1)}c(2)=C2{c1)c,(2)}
2 等价对称元素 若一个对称元素 A 被一个操作变为元素 B,这一操作是由第三个 元素 X 所生成的,当然可以用 X-1把 B 变回 A. A 和 B 两个元素称为 等价. 例如: NH3分子:对称元素:{C3,σv(1),σv(2),σv(3)} σv(1) σv(2) σv(3) H H H C3 σv(1) = σv(2), C3C3 σv(1) = C3 2 σv(1) = σv(3) 所以,三个对称面等价。 3 对称点群 分子点群:对称操作的完全集合构成的群——对称点群。 例 1: G = { σv, σv 2 = E} FONO: Cs点群 单位元: E; 封闭性. σvσv = σv 2 = E, σvE = σv 逆元素. σv -1 = σv 例 2: G = {E, C2, σv(1), σv(2)} H2O: C2V点群 单位元: E 封闭性. σv(1) C2 = C2 σv(1) =σv(2), σv(1) σv(2) = C2 逆元素: C2 -1 = C2, σv -1 = σv 结合律. {C2 σv(1) } σv(2) = C2 {σv(1) σv(2)}
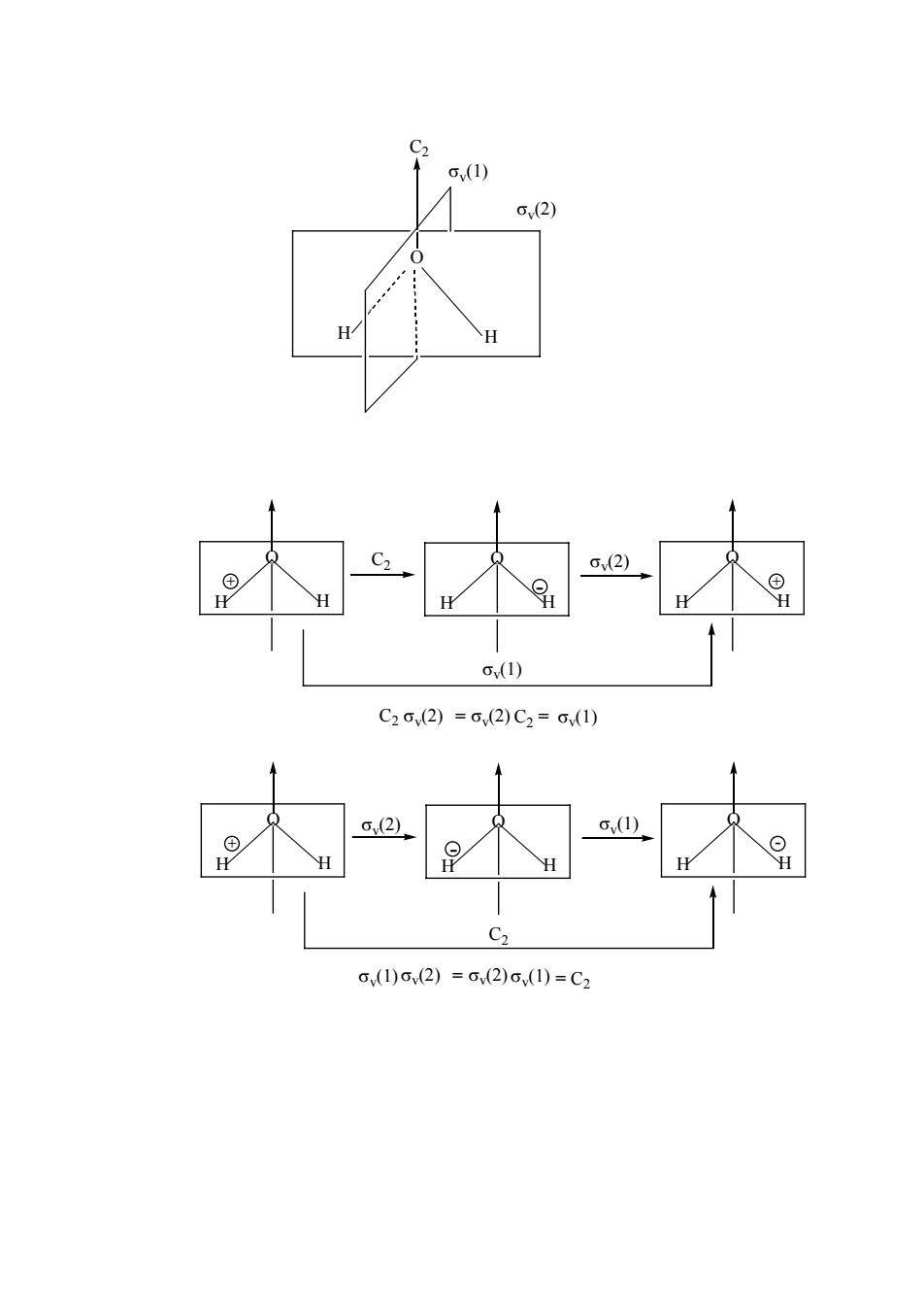
.2 G(1) C2,(2)=G2)C2=(1) C2 c(1)(2)=(2)c(1)=C2
O H H C2 σv(1) σv(2) - O H H C2 + O H H O H H σv(2) + σv(1) O H H C2 + O H H - O H H σv(2) σv(1) - C2 σv(2) σv = = (2) C2 σv(1) C2 σv(2) σv σv(1) = (2) σv(1) =
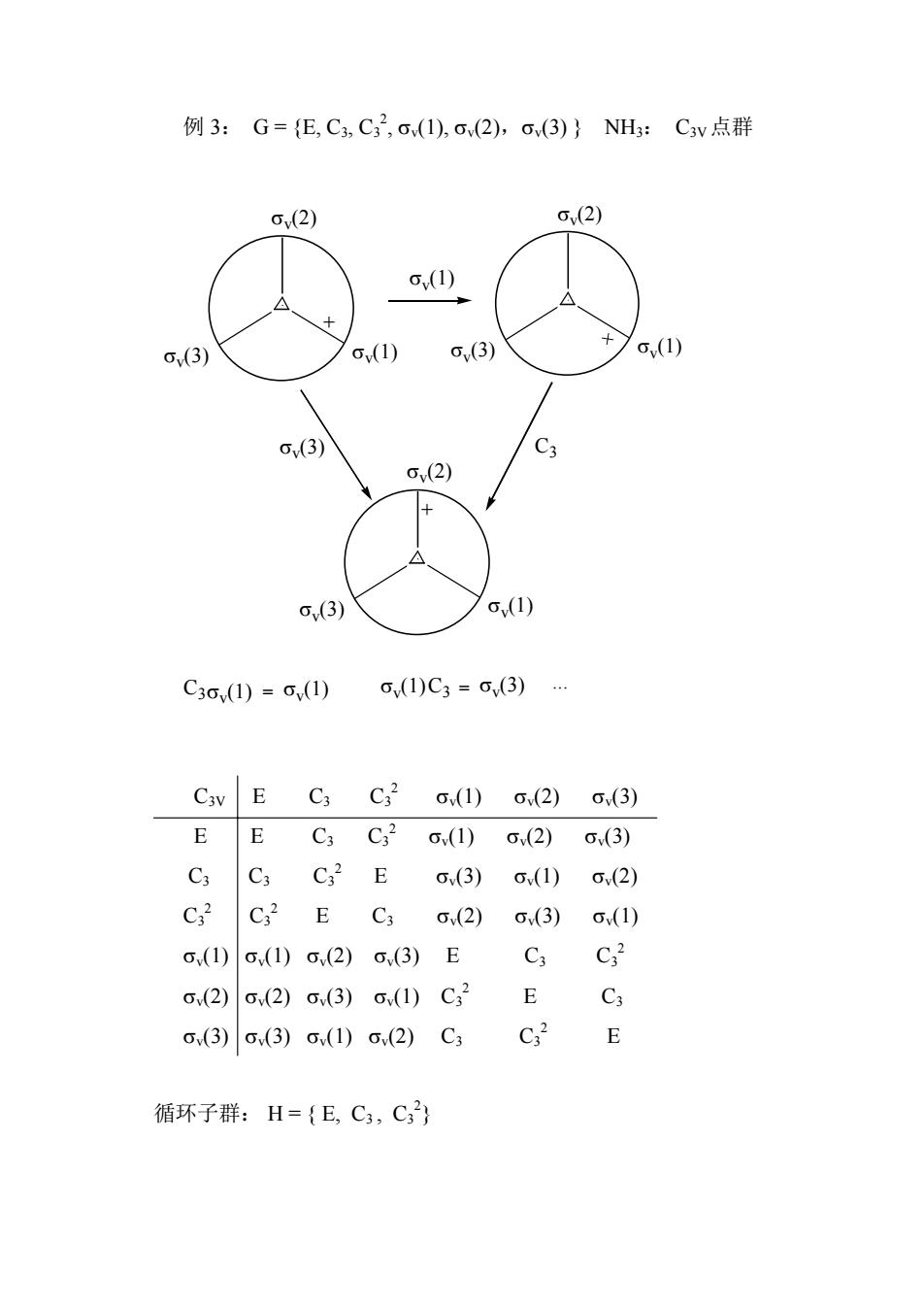
例3:G={E,C,C32,o(1),o(2),G(3)}NH3:C3v点群 0(2) 2) σ(1) o(3) o(1) c(3) o(1) (3) o(2) (3) C361)=o(1) o(1)C3=(3)… Cav E C3 C (1)G(2)G(3) EEC3C,2o(1)c2)o(3) CC3C2Eo.(3)G(1)o(2) C C2 E C3 (2)(3)(10) ()o,().2)(3)ECC2 o(2)o,(2)0(3)6(1)C32EC3 o(3)σ(3)(6.2)C3C2E 循环子群:H={E,C,C)
例 3: G = {E, C3, C3 2 , σv(1), σv(2),σv(3) } NH3: C3V点群 σv(1) σv(2) σv(3) + σv(1) σv(2) σv(3) σv(1) σv(1) σv(2) σv(3) + σv C3 (3) σv C3 (1) = σv(1) σv(1)C3 = σv(3) ... C3V E C3 C3 2 σv(1) σv(2) σv(3) E E C3 C3 2 σv(1) σv(2) σv(3) C3 C3 C3 2 E σv(3) σv(1) σv(2) C3 2 C3 2 E C3 σv(2) σv(3) σv(1) σv(1) σv(1) σv(2) σv(3) E C3 C3 2 σv(2) σv(2) σv(3) σv(1) C3 2 E C3 σv(3) σv(3) σv(1) σv(2) C3 C3 2 E 循环子群: H = { E, C3 , C3 2 }
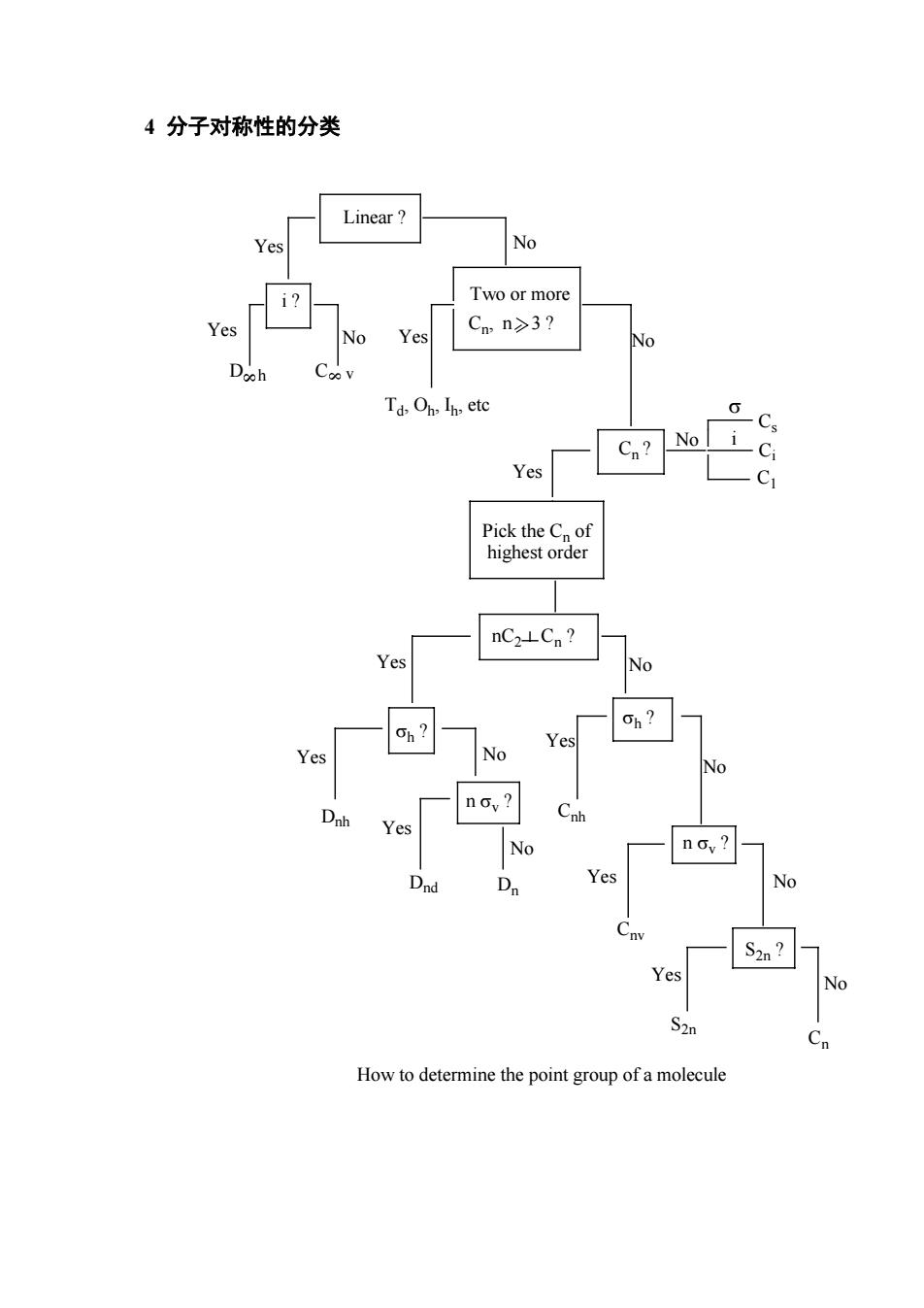
4分子对称性的分类 Linear? Yes i? Two or more Ye Td.Oh-Ih etc Yes ca nC2-Cn? Yes Ch? Ch? Yes No n Gy? Yes No Dnd Dn Yes How to determine the point group of a molecule
4 分子对称性的分类 Linear ? i ? No Two or more Cn, n 3 ? Yes No Yes D h C v Td, Oh, Ih, etc Yes No Cn ? Cs Ci C1 No σ i Pick the Cn of highest order nC2 Cn ? Yes Yes No σh ? n σv ? σh ? Yes No Dnh Yes No Dnd Dn Yes Cnh n σv ? No Yes No Cnv S2n ? Yes No S2n Cn How to determine the point group of a molecule
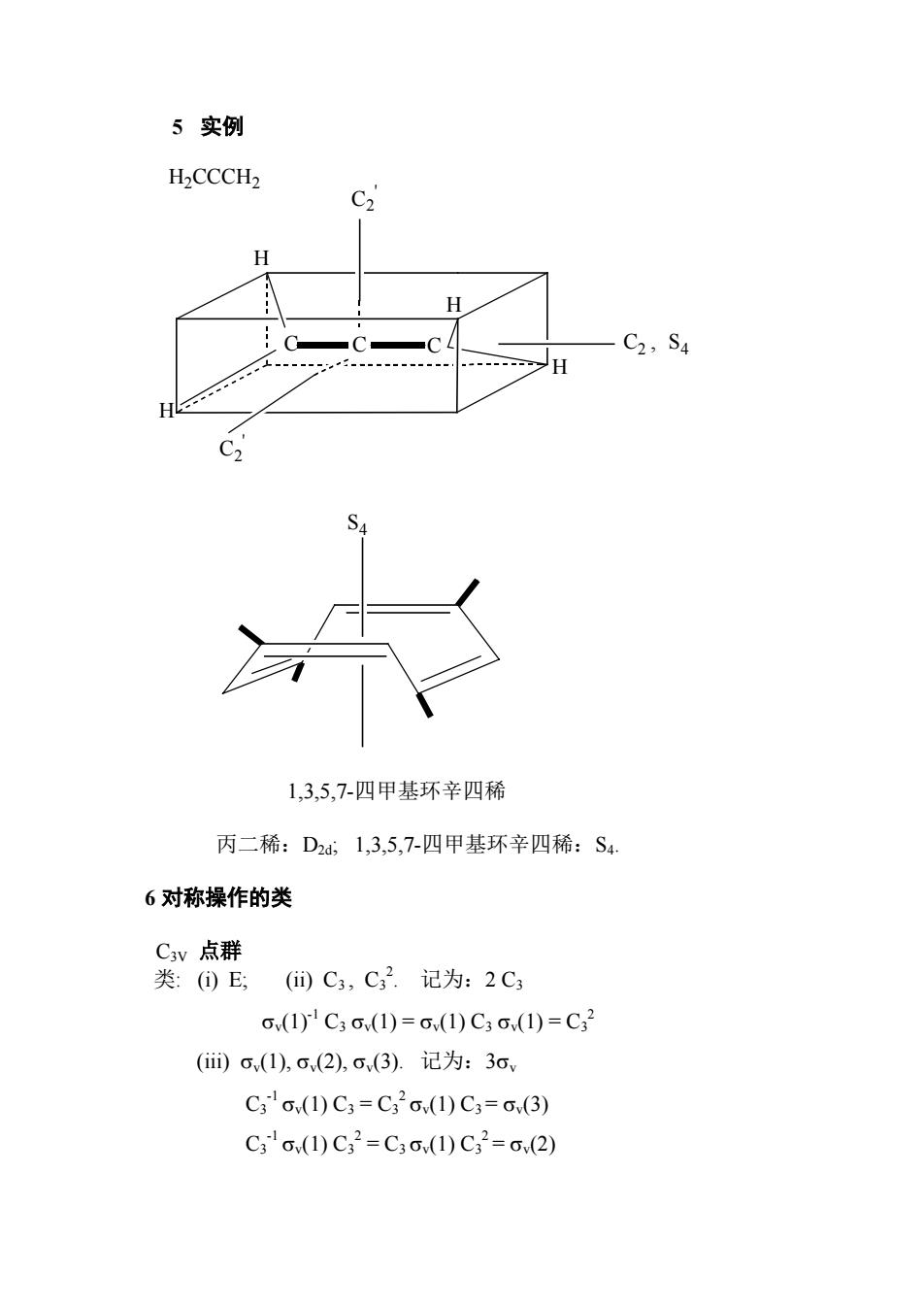
5实例 H>CCCH2 C,1 C2,S4 ..H 1,3,5,7-四甲基环辛四稀 丙二稀:D2d,1,3,5,7-四甲基环辛四稀:S4 6对称操作的类 C3v点群 类:(①E,(C,C2.记为:2C (1)'C3o(1)=o(1)C3o(1)=C2 (ii)o,(1),o(2),o(3).记为:3o C3o(1)C3=C32o(1)C3=o,(3) C3o1)C32=C3o1)C32=o(2)
5 实例 C C C H H H H C2 ' C2 ' C2 , S4 H2CCCH2 S4 1,3,5,7-四甲基环辛四稀 丙二稀:D2d; 1,3,5,7-四甲基环辛四稀:S4. 6 对称操作的类 C3V 点群 类: (i) E; (ii) C3 , C3 2 . 记为:2 C3 σv(1)-1 C3 σv(1) = σv(1) C3 σv(1) = C3 2 (iii) σv(1), σv(2), σv(3). 记为:3σv C3 -1 σv(1) C3 = C3 2 σv(1) C3 = σv(3) C3 -1 σv(1) C3 2 = C3 σv(1) C3 2 = σv(2)
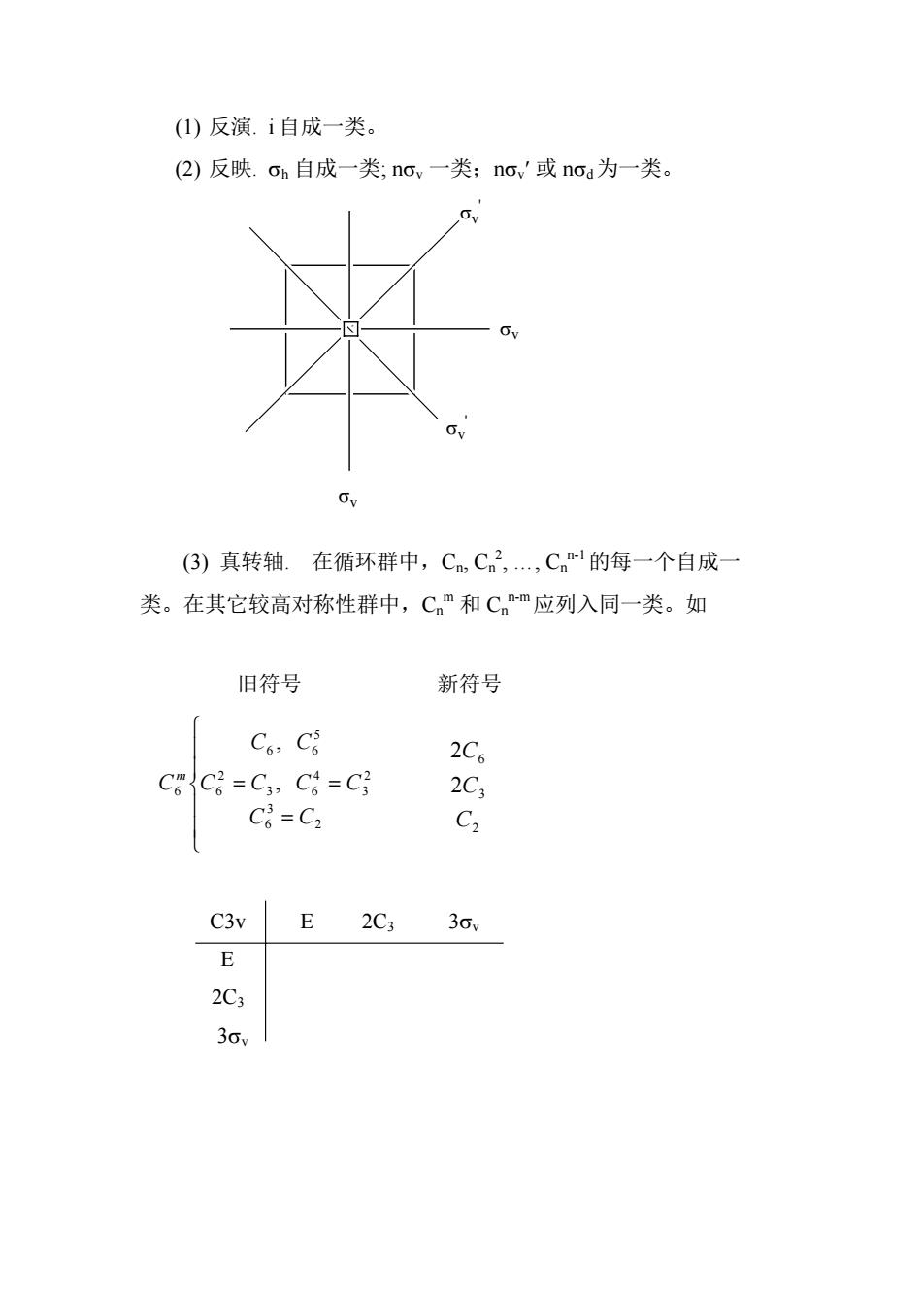
()反演.i自成一类。 (2)反映.oh自成一类;ncv一类;no,'或noa为一类。 (3)真转轴.在循环群中,C,C2,,Cn-的每一个自成 类。在其它较高对称性群中,Cnm和Cm应列入同一类。如 旧符号 新符号 C6,C8 2C6 CC=C3 C4=C3 2C3 C8=C2 C2 C3vE 2C3 30v E 2C3 36
(1) 反演. i 自成一类。 (2) 反映. σh 自成一类; nσv 一类;nσv′ 或 nσd为一类。 σv σv σv ' σv ' (3) 真转轴. 在循环群中,Cn, Cn 2 , …, Cn n-1的每一个自成一 类。在其它较高对称性群中,Cn m 和 Cn n-m应列入同一类。如 旧符号 新符号 = = = 2 3 6 2 3 4 3 6 2 6 5 6 6 6 , , C C C C C C C C C m 2 3 6 2 2 C C C C3v E 2C3 3σv E 2C3 3σv