
Chapter 11酉空间(Unitary Space) l.内积(scalar product) 向量x,yCL,如果复数(x,)满足条件: (1)(xy)=(y,x)° (2)(x,0y)=0(x,y) (ax,y)=(y,ax)"=a'(y,x)"=a'(x,y) (3)(x,+2)=(x,)+(x,2) (4)(x,x)≥0只有当x=0时,(x,x)=0 复数(x,y)则称为向量x和y的内积
Chapter 11 酉空间 (Unitary Space) 1. 内积(scalar product) 向量 x y L , ,如果复数 ( , ) x y 满足条件: * (1) ( , ) ( , ) x y y x (2) ( , ) ( , ) x y x y * * * * ( , ) ( , ) ( , ) ( , ) x y y x y x x y 1 2 1 2 (3) ( , ) ( , ) ( , ) x y y x y x y (4) ( , ) 0 x x 只有当 x=0时, ( , ) 0 x x 复数 ( , ) x y 则称为向量x和y的内积

X X=(4,h,…4n) y2 ,y=((41,2,…un) : Xn yn 2.构造正交归一化的{4,} 1 i=j u,西,)=6,{0i≠j (4,4)组成方阵,正交化 令(u,u,)=1 若(4,w)=a又令4j=u,-04 →(4,4)=(4,4)-a(4,4,)=0
1 1 2 2 1 2 1 2 , , , ( , , ) n n n n x y x y u u u y u u u x y 2. 构造正交归一化的 ui 1 ( , ) 0 i j ij i j u u i j ( , ) i j u u 组成方阵,正交化 ( , ) 1 i i 令 u u ( , ) i j 若 u u ' j j i 又令 u u u ' ( , ) ( , ) ( , ) 0 u u u u u u i j i j i i

归一化:令(4,4)=k 内积x月=(∑w,∑4,∑y,4,少卢∑m,少=XmY 米 X 其中X+=(x,x2,…x)= 转置共轭conjugate transposed
( , ) i i 归一化:令 u u k ' i i u u k 则: ' ' 1 ( , ) ( , ) 1 i i i i k u u u u k k k * * , , ( , ) ( , )= ( , )= = i i j j i j i j i ij j i j i j i j x y x u y u x y u y x m y X mY 内积 1 * * * 2 1 2 ( , , ) n n x x X x x x x 其中 转置共轭 conjugate transposed ~*

由内积定义 0==g4广=则财 Hermitian矩阵 m=m m*is the adjoint(conjugate transposed)of the matrix m(Hermitian conjugate) (AB)=BA" 显然, 由内积(x,x)≥0,有(x,x)=X*mX≥0 m:正定厄米阵, X+mX:正定的厄米型 如果(4,4)=δ x月=Σ,w,y,=∑y=Xy=(Gxx) X= yn Xn
由内积定义 * * ( , ) ( , ) m u u u u m ij i j j i ji m m Hermitian 矩阵 is the adjoint (conjugate transposed) of the matrix m (Hermitian conjugate) m AB B A 显然,由内积 x x, 0 ,有 x x X mX , 0 m: 正定厄米阵, X mX :正定的厄米型 如果 ( , ) i j ij u u 1 * * * * * 2 1 2 , ( , ) ( , ) = , , i i j j i i n i j i n y y x y x u u y x y X Y x x x y 1 2 n x x X x

如果,由正交归一化(orthonormal)基{4}变换为一组新的正 交归一化基{4,即 8=(u.4)=(04:∑a,4广4,4,4,4)=∑44,=2away=0 →A什=AI 或(4,4,…,4)=(4,4,…,24a)) a11a12 … (ay)= a21 a22 a2n (a)= a an2 ain a2n (a,)满足 ∑aka=
如果,由正交归一化(orthonormal)基 变换为一组新的正 交归一化基 ,即 ui ' i u * ' ' * * , , ( , ) ( , )= ( , ) ik ij i j ki k lj l ki lj k l ki lj kl kj ij k l k l k l k u u a u a u a a u u a a a a 1 A A ' ' ' 1 2 1 2 , , , ( , , , )( ) n n ij 或 u u u u u u a * * * 11 12 1 11 21 1 * * * * 21 22 2 12 22 2 * * * 1 2 1 2 ( ) ( ) n n n n ij ij n n nn n n nn a a a a a a a a a a a a a a a a a a a a ( )ij a 满足 * ik jk ij k a a

a-ou- 即aa=1单位矩阵 0 a"a= a"=a 酉矩阵Unitary matrix 3.线性算符表示的性质 线性算符T的伴随算符(adjoint operator) T+定义为:(Txy)=(x,Ty) (对所有xy) 在正交归一化基{4,}下
* ( )ij ik kj jk ik ij k k a a a a a a a a 1 即 单位矩阵 1 0 0 0 1 0 1 a a 1 a a 酉矩阵Unitary matrix 3. 线性算符表示的性质 线性算符T的伴随算符(adjoint operator) T 定义为: Tx y x T y , ( , ) (对所有x, y) 在正交归一化基 ui 下

(x,月=(∑47x∑44)=∑了.4,4,)=∑Ty x,T列=(∑4∑7)=∑7aw,)=E74=∑7 上述两式有:T=T→T+=产 其中T+为伴随算符,了为转置共轭 在正交归一化基下,伴随算符的表示就是算符T,表示矩阵 的共轭转置。 如果T+=T,即(Tx,y)=(x,Ty),则称T为自伴随的(self一adjoint) 或厄米的(Hermitian)。U算符(Unitary operator:小对任意的x,y有: (Ux,Uy)=(x,y) 在正交归一化坐标下,U的表示矩阵是酉矩阵,即U+U=UU+=1
* * * * , , , , , ( , ) ( , ) i ij j k k ij j k i k ij j i i j k i j k i j Tx y u T x u y T x y u u T x y * * * , , , , , ( , ) ( , ) ( , ) i i j jk k i jk k i j i jk k j ji i i j k i j k i k i j x T y x u u T y x T y u u x T y x T y 上述两式有: * * T T T T ji ij 其中 T 为伴随算符, T * 为转置共轭 在正交归一化基下,伴随算符的表示就是算符 ,表示矩阵 的共轭转置。 T 如果 ,即 ,则称T为自伴随的(self—adjoint) 或厄米的(Hermitian)。 U算符(Unitary operator):对任意的x, y有: T T Tx y x Ty , ( , ) ( , ) ( , ) Ux Uy x y 在正交归一化坐标下,U 的表示矩阵是酉矩阵,即 U U UU 1

4.表示的酉化(Unitary representations). 对任意一对矢量{x,y},定义 {x,y=1∑(D(Rx,D(R) RCG 显然,{x,y}满足内积的定义,对群G中元素S有: (D(S),D(S)(D(R)D(S),D(R)D(S))=(D(RS),D(RS)y) RCG RCG 因为RScG,当R遍及群G所有元素时,RS也遍及群G,即求和不变 (D(S)x.D(S)=(D(RS)x.D(RS)y) RCG (D(R)x,D(R)y)={x,y} REG 即表示算符{D(R)}是酉算符(其表示矩阵是U矩阵)
4. 表示的酉化(Unitary representations) 对任意一对矢量 { , } x y ,定义 1 { , } ( ( ) , ( ) ) R G x y D R x D R y g 显然, { , } x y 满足内积的定义,对群 中元素 有: 1 1 { ( ) , ( ) }= ( ( ) ( ) , ( ) ( ) )= ( ( ) , ( ) ) R G R G D S x D S y D R D S x D R D S y D RS x D RS y g g 因为 RS G , 当 R遍及群G所有元素时, RS也遍及群G, 即求和不变 G S 1 { ( ) , ( ) } ( ( ) , ( ) ) 1 ( ( ) , ( ) )={ , } R G R G D S x D S y D RS x D RS y g D R x D R y x y g 即表示算符 { ( )} D R 是酉算符(其表示矩阵是 U 矩阵)

令 {4,u}=δ={y,Vj} 列=∑4524y 相对于内积(x,y)相对于内积{x,} 定义算符T将{4}交换为{y} =∑∑w (y,V2,…vn)=T(4,42,…n) =∑y}=∑ =(4,h2,…4n)Tg)nx =X+Y=(x,y) 因为{Tx,Ty}=(x,y) 对于等价表示D(S)=T-D(S)T (T-D(S)Tx,T-D(S)Ty=D(S)Tx,D(S)Ty)-Tx,Ty-(x,y) 如果定义D(S)=T-D(S)T (D(S)x,D(S)y)=(x,y) D(S)满足U表示
{ , } { , } i j ij i j 令 u u v v 相对于内积(x, y) 相对于内积{x, y} 定义算符 T 将 { } u1 交换为 1 { } v 1 2 1 2 1 2 ( , , ) ( , , ) ( , , )( ) n n n ij n n v v v T u u u u u u T 因为 { , } ( , ) Tx Ty x y 对于等价表示 ' 1 D S T D S T ( ) ( ) 1 1 ( ( ) , ( ) )={ ( ) , ( ) }={ , }=( , ) T D S Tx T D S Ty D S Tx D S Ty Tx Ty x y 如果定义 ' 1 D S T D S T ( ) ( ) ' ' ( ( ) , ( ) ) ( , ) D S x D S y x y ' D S( ) 满足 U 表示。 , , * * , { , } , , , ( , ) i ij j k kl l i j k l j j l l j l j l j l j j j l j Tx Ty u T x u T y v x v y x y v v x y X Y x y
Chapter 12表示的约化及其判据 V群的表示 V e a b C e e a b 0 a e b b b e a b a e 1 00 0 0 100 0 010 0 00 0 10 0 1 0 0 0 0 001 0 01 0 (e,a,b,c) 0 010 0 001 100 0 01 00 0 00 1 0 010 0100 1000 (e,a,b,c) (a,e,c,b) (b,c,e,a) (c,b,a,e)
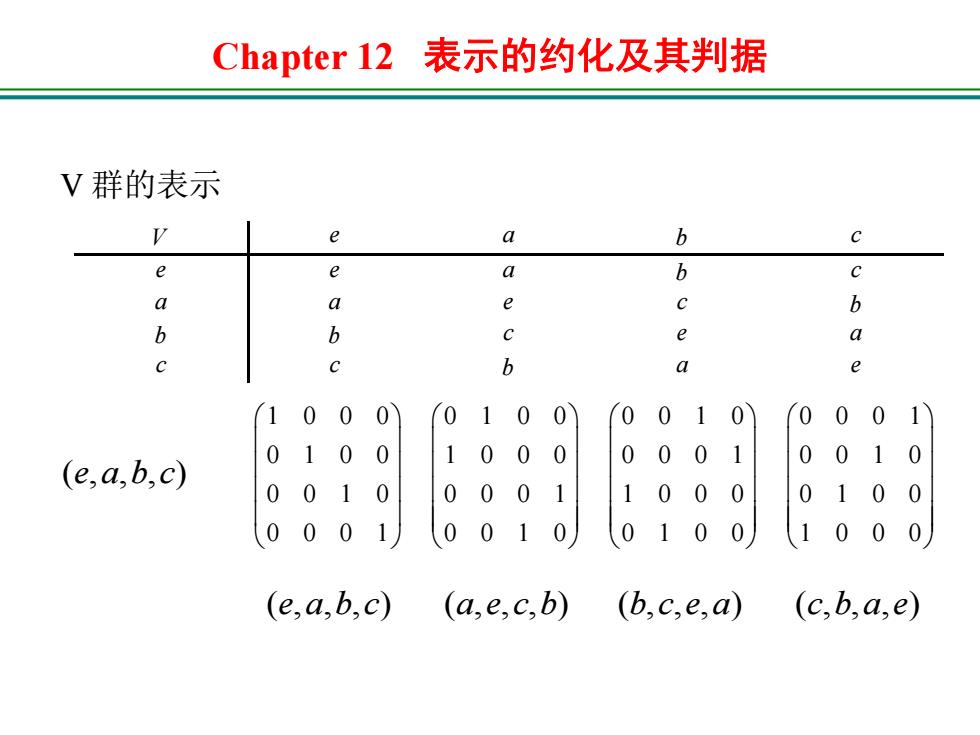
Chapter 12 表示的约化及其判据 V 群的表示 V e a b c e e a b c a a e c b b b c e a c c b a e ( , , , ) e a b c 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0 ( , , , ) e a b c ( , , , ) a e c b ( , , , ) b c e a ( , , , ) c b a e