厦门大学：《结构化学 Structural Chemistry》课程教学资源（课件讲稿）Chapter 2 Atomic Structure

Chapter 2 Atomic Structure

Chapter 2 Atomic Structure

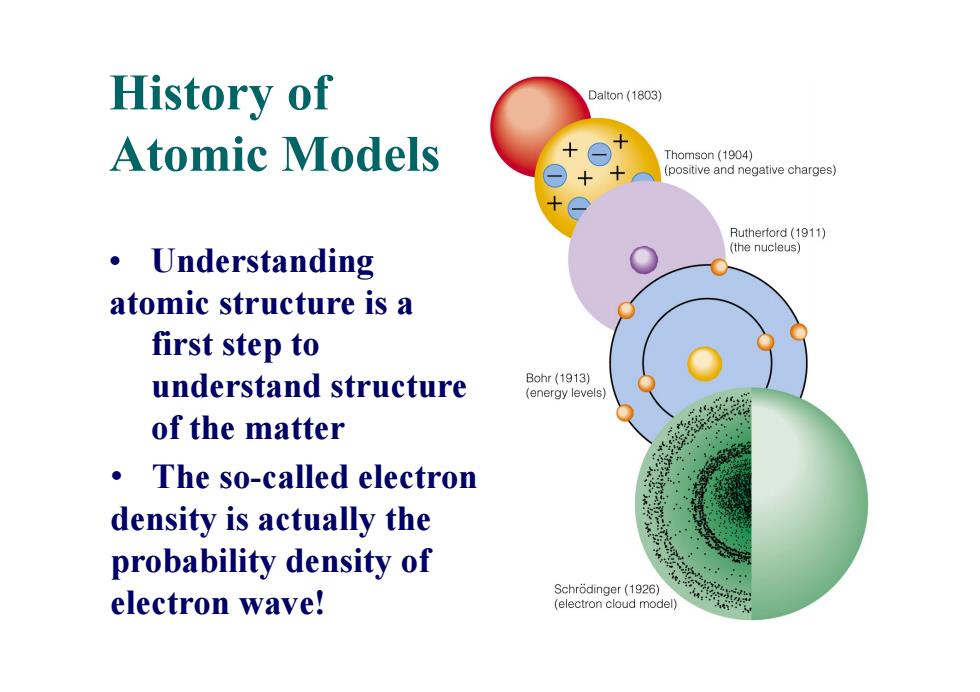
History of Dalton (1803) Atomic Models Thomson(1904) (positive and negative charges) Rutherford(1911) Understanding (the nucleus) 。 atomic structure is a first step to understand structure Bohr(1913) (energy levels) of the matter The so-called electron density is actually the probability density of Schrodinger(1926) electron wave! (electron cloud model)

History of Atomic Models • Understanding atomic structure is a first step to understand structure of the matter • The so-called electron density is actually the probability density of electron wave!

2.1 The Schrodinger equation and its solution for one-electron atoms 2.1.1 The Schrodinger equation The Hamiltonian Operator of one-electron atoms H atom,Het and Li2+ 月=i+元+。= 2mn V2+V-e e The reduced mass u= M·me 1836m。 ≈0.999m。 M+me (1+1836)m

2.1 The Schrödinger equation and its solution for one-electron atoms 2.1.1 The Schrödinger equation The Hamiltonian Operator of one-electron atoms H atom, He + and Li2+ e n e e n n n e n e V m m H  T  T  V         ˆ 2 2 ˆ ˆ ˆ ˆ 2 2 2 2   1836 0.999 (1 1836) e e e e e Mm m m Mm m       The reduced mass e n

Consider that the electron approximately surrounds the atomic nucleus,the Hamilton operator can be simplified as 、 +n 2m。 = 方2 2 2m。x+ n-e Ze2 e n-e 4π8o' r=vx2+y2+22 The Schrodinger equation Hy =Ew Separation of variables

e n e e e n e V m H  T V       ˆ 2 ˆ ˆ ˆ 2 2  r Ze Vn e 0 2 4 ˆ     Consider that the electron approximately surrounds the atomic nucleus, the Hamilton operator can be simplified as r e 2 2 2 r  x  y  z 2 n-e 2 2 2 2 2 e 2 V ˆ ) x y z ( 2m H - ˆ            Separation of variables ? The Schrödinger equation Hˆ  E

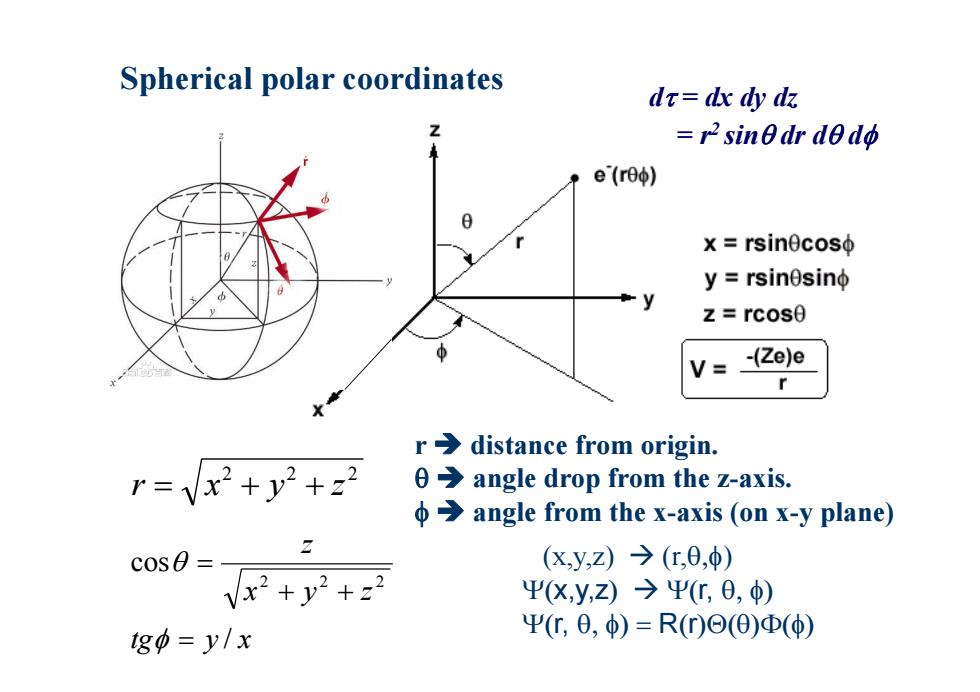
Spherical polar coordinates dr-dx dy dz Z r2 sin0dr dedo e(reo) X=rsinθcoso y=rsinθsino z=rcosθ V= -(Ze)e X r>distance from origin. r=vx2+y2+22 0>angle drop from the z-axis. φ→angle from the x-axis(onx-y plane) c0s0= (xy,z）→(c,0,φ) Vx2+y2+22 Ψ(X,y,Z）→ΨC,0,) tgo=y/x Ψ，0，φ)=R(0)⊙(0)Φ（φ）

Spherical polar coordinates 2 2 2 r  x  y  z (x,y,z)  (r, ) x,y,z  r,  r,  R  r r  distance from origin.   angle drop from the z-axis.   angle from the x-axis (on x-y plane) 2 2 2 cos x y z z     tg  y / x d = dx dy dz = r2 sin  dr d d

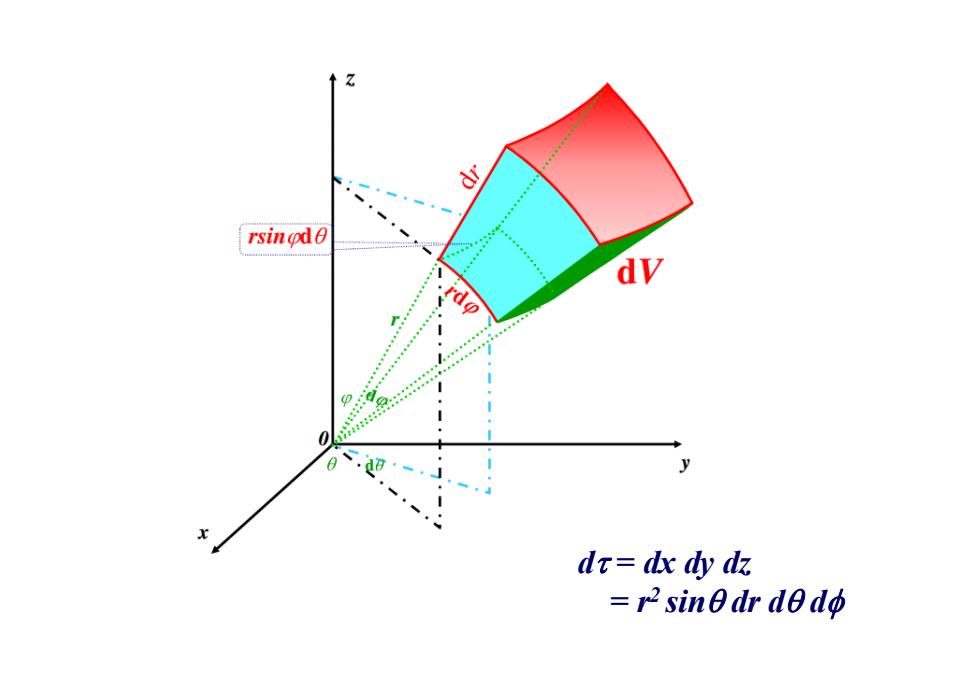
dr rsingd dV rdo p dr=dx dy dz =r2sinθdr de do

d = dx dy dz = r2 sin  dr d d

Partial derivatives x=rsinecoso r=vx2+y2+22 y=r sinesing z=rcos0 c0S0= Vx2+y2+22 tgo=y/x +y2+22)i2x==sin0c0s0 ∂0 -sin0 Ox a0cosθcosp 8x

Partial derivatives 2 2 2 r  x  y  z 2 2 2 cos x y z z     tg  y / x x = r sin cos y = r sin sin z = r cos ( ) 2 sin cos 21 21 2 2 2        rx x y z x xr x r r zx z x y z x x      cos cos )( ) 2 21 sin ( 3 2 2 2 3/ 2             

Spherical polar coordinates dx ax or dx 80 ox op a.cos0cosφo sino a =sin0cosφ Or 00 rsine do =sinosin 0+cos8sinp.0+cos中.0 3 00 rsine 0d a =cos0o sino o 0z Or r 60 72 10 1 1 r20 (sin 2 Or r2 sine 00 a0 r2sin20002 Ze2 n-e (4πE)r 1 1 1 r2 or ay+8πm(E+ Or o(sin+r sin2e 062 r2sine 80 a0 Ze'=0 4π6I

Spherical polar coordinates () ( ) ( ) r x xr x xp                cos cos sin sin cos rr rsin                 cos sin cos sin sin y rr rsin                               z r r sin cos 2 2 2 2 2 2 2 2 sin 1 (sin ) sin 1 ( ) 1                     r r r r r r 2 0 (4 ) n e Ze V  r    The Schrödinger equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 m e Ze r E rr r r r h r                       

2.1.2 The solution---separation of variables SubstituteΨc,0,Φ)=R(ro(o)Φ（φ）into the equation 1 ay8πm(E+ r2 or r2sine 00 00 r2sin20062 h2 Zew=0 4π8' 2 and multiply with R(r)⊙(0)Φ() 1 oR) 1 + oΦ(@8元m(E+ R(r)or or ⊙(0)sin0a (sin) a0Φ()sin20ap2 h2 er2=0 π' 1 (r2R( 8mle(E+4π ze2 )r2=[ 1 (sin 1 a2Φ（φ） )+ R(r）ar (e)sine a0 ae Φ(p)sin20ap2

2.1.2 The solution --- separation of variables Substitute r,  R  r into the equation 2 2 2 2 2 2 22 2 2 0 11 1 8 ( ) (sin ) ( ) 0 sin sin 4 m e Ze r E rr r r r h r                        and multiply with ( ) ( ) ( ) 2 R r     r ) 0 4 ( ( ) 8 ( )sin 1 ) ( ) (sin ( )sin 1 ) ( ) ( ( ) 1 2 0 2 2 2 2 2 2 2                    r r ze E h m r R r r R r r e             ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 0 2 2 2 2                                r r ze E h m r R r r R r r e

1 (rR((E (sin) 1 a2Φ（中） R(r）ar Or h2 4π6' (e)sine a0 a0 Φ()sin20ap2 1 let ((r) ( 8元2m2(E+ e )r2= R(r)or Or h2 4πEJ Radial part a (sin0 o0(8) a2Φ(p) + Angular part (0)sine a0 a0 Φ(p)sin20ap2 multiplied sin20 sine sin6o0②)+1 ⊙(0)a a01 ()=-Bsin20 ()62 sine o (sin) 80)+Bsin'0=- 1 aΦ(p) ⊙(0)a D()8d2 sine 6 let (sin+Bsinm (Θ ⊙(0)a a0 eq) 1 aΦ(）=-m ()02

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 ( ) ( ) 1 ) sin ( .) ( ) (sin ( ) sin ( ) ( ) 1 ) sin ( ) (sin ( ) sin sin ( ) ( ) 1 ) ( ) (sin ( ) sin sin ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) ( .) 4 ( 8 ) ( ) ( ( ) 1 m let m eq multiplied r R eq r ze E h m r R r r R r r let e                                                                                                      ] ( ) ( )sin 1 ) ( ) (sin ( )sin 1 ) [ 4 ( 8 ) ( ) ( ( ) 1 2 2 2 2 02 22 2                           r r ze E h m r R r r R r r e Angular part Radial part