
Chapter 7 Electronic Structure of Diatomic Molecules 7.1 The Hydrogen Molecule Ion 1.Accurate solutions a 0 R b The H2*molecule.The nuclei are at a and b;R is the internuclear distance;roand ro are the distances from the the electron to nuclei a and 6 In the BO approximation,the Hamiltonian in atomic units is =-12-1-1+1 2 a店R Since the nuclei are fixed,1/R is a constant.The purely electronic Hamiltionian for H2can be rewritten as He1= 12 11 Ta Ih (7.1) Obviously,the Schroedinger equation is not separable in spherical polar coordinates.In 1927,Burrau showed that the separation of variables is possible using confocal elliptic coordinates.n.. g a The elliptic coordinates with two centers
Chapter 7 Electronic Structure of Diatomic Molecules 7.1 The Hydrogen Molecule Ion 1. Accurate solutions . . a b O R -e φ r ra rb The H2 + molecule. The nuclei are at a and b; R is the internuclear distance; ra and rb are the distances from the the electron to nuclei a and b. In the BO approximation, the Hamiltonian in atomic units is r r R H a b 1 1 1 2 1 2 = − ∇ − − + ∧ Since the nuclei are fixed, 1/R is a constant. The purely electronic Hamiltionian for H2 + can be rewritten as a b el r r H 1 1 2 1 2 = − ∇ − − ∧ (7.1) Obviously, the Schroedinger equation is not separable in spherical polar coordinates. In 1927, Burrau showed that the separation of variables is possible using confocal elliptic coordinates ξ,η,ϕ. . . a R b ra rb The elliptic coordinates with two centers ϕ

5=名+名 7=名6 R R (7.2) The ranges of these coordinates are: 0≤p≤2π,1≤5≤0,-1≤n≤1 (7.3) We have =2R(5+) 5=25-) (7.4) The H2*electronic Hamiltonian(7.1)in the elliptic coordinates has the form Hd=- 2 R2(E2-72) +2是+0-) -2 n 1102 2 2(7.5) -2&+g-11-7002RE+m)RE-》7 Hence the Schroedinger equation is HΨ(5,n,p)=EΨ(5,n,p) (7.6) Let Ψ(5,n,p)=L(5)M(n)Φ(p) (7.7) Substitution of(7.7)into the Schroedinger equation (7.6)leads to an equation in which the variables are separable d2 D(p)=-m2D(o) do" (7.8) m2 (g-224+25+,Rg-2L=079
R r r R r r a b a − b = + ξ = , η (7.2) The ranges of these coordinates are: 0 ≤ ϕ ≤ 2π , 1 ≤ ξ ≤ ∞, −1 ≤ η ≤ 1 (7.3) We have ( ) 2 1 ( ), 2 1 ra = R ξ +η rb = R ξ −η (7.4) The H2 + electronic Hamiltonian (7.1) in the elliptic coordinates has the form ( ) 2 ( ) 2 ) ] 1 1 1 1 2 ( [( 1) 2 (1 ) ( ) 2 2 2 2 2 2 2 2 2 2 2 2 2 2 η ξ η ϕ ξ η ξ η η η η ξ ξ ξ ξ ξ η − − + − ∂ ∂ − + − + ∂ ∂ − ∂ ∂ + − ∂ ∂ + ∂ ∂ − − = − ∧ R R R Hel (7.5) Hence the Schroedinger equation is Ψ(ξ,η,ϕ) = Ψ(ξ,η,ϕ) ∧ el H el E (7.6) Let Ψ(ξ,η,ϕ) = L(ξ )M (η)Φ(ϕ) (7.7) Substitution of (7.7) into the Schroedinger equation (7.6) leads to an equation in which the variables are separable. ( ) ( ) 2 2 2 ϕ ϕ ϕ Φ = −m Φ d d (7.8) ) 0 2 1 1 ( 1) ' ' 2 ' ( 2 2 2 2 2 2 = − − + + + + − L m L L A R EelR ξ ξ ξ ξ ξ (7.9)

()M-2M-(4RM0 10 Solving the equation(7.8),we have (p)= V2π (7.11) where m=0,±l,+2,.. [1 when m=0 √2π (p)= -cosmo V2 when m 1,2... (7.12) √2 -sin mo The solution for M(n)is an infinite series of associated Legendre functions.L()also involves an infinite series.The requirement that the wave function be well behaved leads to the conclusion that for a fixed value of R,only certain values of Ee are allowed (i.e.discrete);this gives a series of electronic states,corresponding electronic energy E(R)=E+ R (7.13) The electronic energies must be calculated numerically.The series of energy levels are marked by quantum numbers n,I,and m,whose allowed values are n=1,2,3,… l≤n-1 (7.14) m≤I 10,1,2,3,… s,p,d,f
) 0 2 1 1 (1 ) ' ' 2 ' ( 2 2 2 2 2 = − − − − + + M m M M A EelR η η η η (7.10) Solving the equation (7.8), we have ϕ π ϕ im e 2 1 Φ( ) = (7.11) where m = 0, ±1, ±2, … or = Φ = ϕ π ϕ π π ϕ m m when m sin 2 1 cos 2 1 0 2 1 ( ) when m = 1, 2, … (7.12) The solution for M(η) is an infinite series of associated Legendre functions. L(ξ) also involves an infinite series. The requirement that the wave function be well behaved leads to the conclusion that for a fixed value of R, only certain values of Eel are allowed (i.e. discrete); this gives a series of electronic states, corresponding electronic energy R E R Eel 1 ( ) = + (7.13) The electronic energies must be calculated numerically. The series of energy levels are marked by quantum numbers n, l, and m, whose allowed values are m l l n n ≤ ≤ − = 1 1, 2, 3, " (7.14) l 0, 1, 2, 3, … s, p, d, f. …
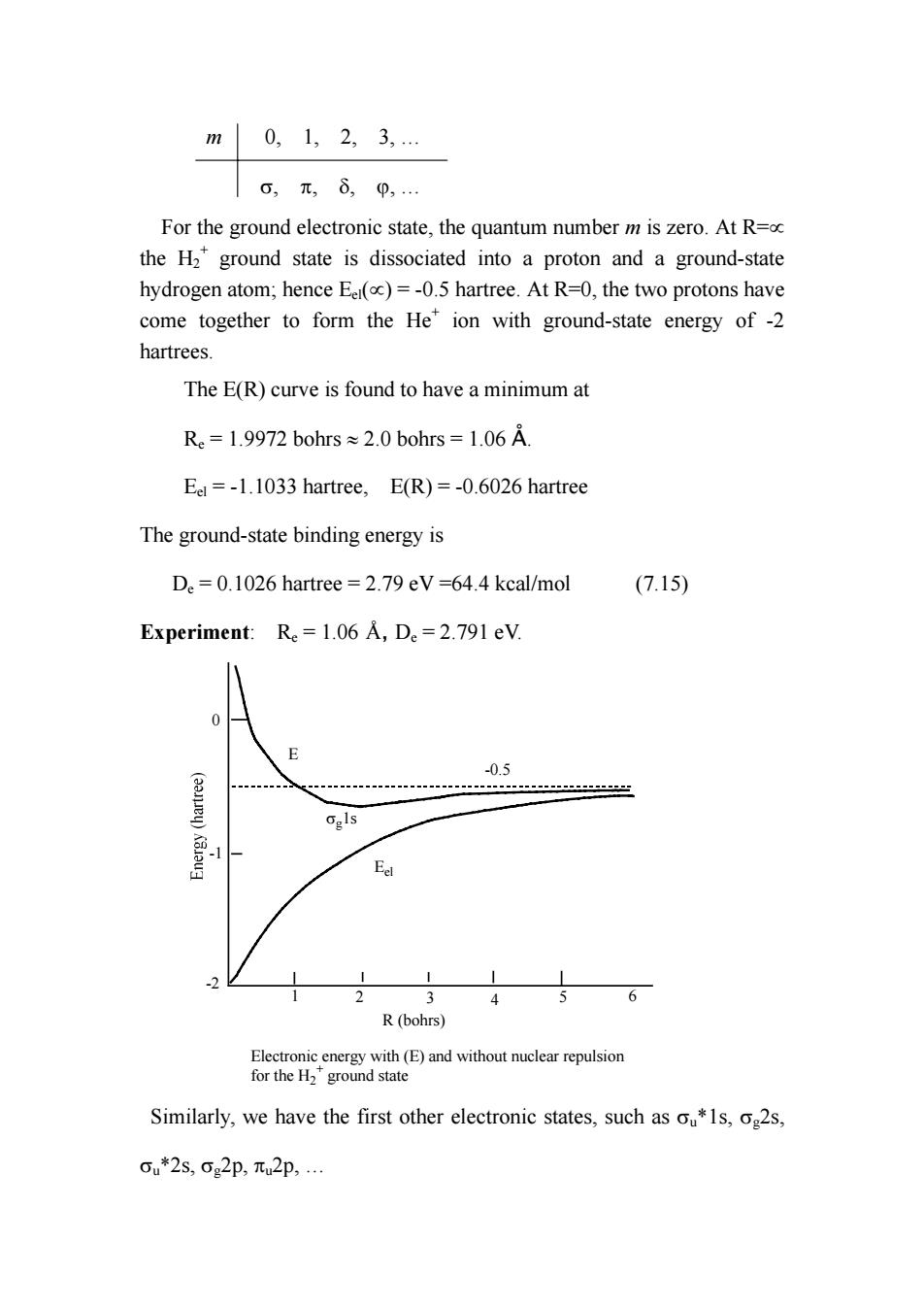
m0,1,2,3, o,元,80,… For the ground electronic state,the quantum number m is zero.At R= the H2*ground state is dissociated into a proton and a ground-state hydrogen atom;hence Eer(oc)=-0.5 hartree.At R=0,the two protons have come together to form the He*ion with ground-state energy of-2 hartrees. The E(R)curve is found to have a minimum at Re=1.9972 bohrs 2.0 bohrs 1.06 A. Eel=-1.1033 hartree,E(R)=-0.6026 hartree The ground-state binding energy is D.=0.1026 hartree =2.79 eV=64.4 kcal/mol (7.15) Experiment:Re=1.06 A,De=2.791 eV. 0.5 Ggls E 3 456 R(bohrs) Electronic energy with(E)and without nuclear repulsion for the H2 ground state Similarly,we have the first other electronic states,such as s,o2s. ou*2s,cg2p,元u2p
m 0, 1, 2, 3, … σ, π, δ, ϕ, … For the ground electronic state, the quantum number m is zero. At R=∝ the H2 + ground state is dissociated into a proton and a ground-state hydrogen atom; hence Eel(∝) = -0.5 hartree. At R=0, the two protons have come together to form the He+ ion with ground-state energy of -2 hartrees. The E(R) curve is found to have a minimum at Re = 1.9972 bohrs ≈ 2.0 bohrs = 1.06 Å. Eel = -1.1033 hartree, E(R) = -0.6026 hartree The ground-state binding energy is De = 0.1026 hartree = 2.79 eV =64.4 kcal/mol (7.15) Experiment: Re = 1.06 Å, De = 2.791 eV. 0 -1 -2 R (bohrs) 1 2 3 4 5 6 Eel E Electronic energy with (E) and without nuclear repulsion for the H2 + ground state σg1s -0.5 Similarly, we have the first other electronic states, such as σu*1s, σg2s, σu*2s, σg2p, πu2p, …

2.Approximate Treatment of the H2" Trial function: Consider a limiting behavior of the H2*ground-state electronic wave function as R approaches p=CalSa +CplSp (7.16) -e-n When R goes zero,we get the He'ion,which has the ground-state wave function(Z=2) 2 1\π (7.17) Note that at the R=0the trial function(7.16)goes to (G+c2) e V Comparing with (7.17),we see that (7.16)has the wrong limiting behavior at R =0.We can fix things by multiplying ra and ro in the exponentials by a variational parameter k=k(R).For correct limiting behavior at zero and infinite internuclear distance,we have K(0)=2,k(oc)=1 We thus take as the trial function 0=Ca功sa+C691sb (7.18) where k 4π -e-kn (7.19)
2. Approximate Treatment of the H2 + Trial function: Consider a limiting behavior of the H2 + ground-state electronic wave function as R approaches ∝. a a b b ϕ = c 1s + c 1s (7.16) a br b r a s e s e − − = = π π 1 , 1 1 1 When R goes zero, we get the He+ ion, which has the ground-state wave function (Z=2) r e 2 3 2 − π (7.17) Note that at the R = 0 the trial function (7.16) goes to r c c e− + π 1 ( ) 1 2 . Comparing with (7.17), we see that (7.16) has the wrong limiting behavior at R = 0. We can fix things by multiplying ra and rb in the exponentials by a variational parameter k = k(R). For correct limiting behavior at zero and infinite internuclear distance, we have K(0) = 2, k(∝) =1 We thus take as the trial function a sa b sb c c ϕ = φ1 + φ 1 (7.18) where a b kr sb kr sa e k e k − − = = π φ π φ 3 1 3 1 , (7.19)

The molecular orbital (MO)(7.18)is a linear combination of atomic orbitals,an LCAO-MO.(Exponential parameter-effective nuclear charge) For the trial function(7.18),the secular equation is H-WS.H-WS=0 Hba-WSba Hob-WSpb (7.20) The integrals Haa and Hob are Hnm=∫4nH4ndk,Hb=∫4ibH4dy(I.21)) These two integrals are called Coulomb integrals.Since the H2'is a homonuclear diatomic system,Han=Hob.We have Hb=∫gaH4bdy,Ha=∫4bH4dy(7.22) Since is Hermitian and the functions in these integrals are real,we conclude that Hab=Hpa.The integral Hab,is called a resonance (or bond) integral.Sinceand are normalized and real.We have Sa==pi中1adh=1=Sb Sab=∫gin中i6dr=Sba (7.23) The secular equation(7.20)becomes H-W Ha-WS.=0 Hab -WSab Hoo-W (7.24) Hoo -W=(Hob-SabW) (7.25) 所-月tH4,所-二H 1+Sab 1-Sh (7.26) These two roots are upper bounds for the energies of the ground and the first excited electronic states of H2
The molecular orbital (MO) (7.18) is a linear combination of atomic orbitals, an LCAO-MO. (Exponential parameter—effective nuclear charge) For the trial function (7.18), the secular equation is = 0 − − − − ba ba bb bb aa aa ab ab H WS H WS H WS H WS (7.20) The integrals Haa and Hbb are Haa φ sa Hφ sadν Hbb φ sb Hφ1sbdν * 1 1 * 1 , ∫ ∫ ∧ ∧ = = (7.21) These two integrals are called Coulomb integrals. Since the H2 + is a homonuclear diatomic system, Haa = Hbb. We have Hab φ sa Hφ sbdν Hba φ sb Hφ1sadν * 1 1 * 1 , ∫ ∫ ∧ ∧ = = (7.22) Since ∧ H is Hermitian and the functions in these integrals are real, we conclude that Hab = Hba. The integral Hab is called a resonance (or bond) integral. Since φ1sa and φ1sb are normalized and real. We have ab sa sb ba aa sa sa sa sa bb S dv S S dv S = = == = = ∫ ∫ 1 * 1 1 * 1 | 1 1 1 φ φ φ φ φ φ (7.23) The secular equation (7.20) becomes = 0 − − − − H WS H W H W H WS ab ab aa aa ab ab (7.24) H W (H S W ) aa − = ± ab − ab (7.25) ab aa ab ab aa ab S H H W S H H W − − = + + = 1 , 1 1 2 (7.26) These two roots are upper bounds for the energies of the ground and the first excited electronic states of H2 +

We now find the coefficients in (7.18)for each of the roots of the secular equation.From the linear homogeneous equations in Chapter 5, we have (H-W)c+(Hh-S)c=0 (7.27 Substituting in W from(7.26),we get Ca=l Co (7.28) =Ca(Osa +oisb) (7.29) We fix ca by normalization: cP∫(2++244h)d=1 Ico (7.30) 2+28 The normalized trial function corresponding to the energy W is thus: 1 01= =(9a+中b) V2+2S (7.31) For the root W2,we find c=-co and 1 0=2-2 =(4La-1b) (7.32) Let us evaluate Haa,Hab,and Sab Overlap integral Sat Sw=e1+R+片2R] (7.34) Coulomb integral Haa (7.35) Resonance integral Hab
We now find the coefficients in (7.18) for each of the roots of the secular equation. From the linear homogeneous equations in Chapter 5, we have ( − ) + ( − ) = 0 aa a ab ab b H W c H S c (7.27) Substituting in W1 from (7.26), we get = 1 b a c c (7.28) ( ) 1 a 1sa 1sb ϕ = c φ +φ (7.29) We fix ca by normalization: ab a a sa sb sa sb S c c dv 2 2 1 | | | | | ( 2 ) 1 1 1 2 1 2 1 2 1 1 + = = + + ⋅ = ∫ ϕ ϕ φ φ φ φ (7.30) The normalized trial function corresponding to the energy W1 is thus: ( ) 2 2 1 1 1sa 1sb ab S ϕ φ + φ + = (7.31) For the root W2, we find cb = -ca and ( ) 2 2 1 2 1sa 1sb ab S ϕ φ −φ − = (7.32) Let us evaluate Haa, Hab, and Sab. Overlap integral Sab ] 3 1 [1 2 2 S e kR k R kR ab = + + − (7.34) Coulomb integral Haa ) 1 ( 1 2 1 2 2 R e k R H k k kR aa = − − + + − (7.35) Resonance integral Hab

H=号25+6k-2+Re" (7.36) The final task is to vary the parameter k,setting =0,a亚=0 k ak The results are that for the (Is+1sp)function(7.31),the parameter k increases monotonically from I to 2 as R decreases from to 0;for the 2(1s -1sp)function(7.32),k decreases monotonically from 1.0 to 0.4 as R decreases from to 0.Since k is positive and never greater than 2,and since the overlap integral Sab is positive,we see from (7.36)that the resonance integral Hb is always negative. The ground state o1s m=H。+H幽 1 1+Sab 01= V2+2S =(91a+41b) k(R)=1.24 Re=2.02 bohrs,Binding energy:2.35 eV.(Expt.2.00 bohrs,2.79 eV). If we omit varying k,but simply set it equal to 1,we get Re=2.50 bohrs,Binding energy:1.76 eV The excited state ou 1s m=H。-Hb V2-254.4) 1 1-Sab The appearance of the trial functions for og Is and ouls
kR ab ab H k S k k kR e− = − + ( − 2)(1+ ) 2 1 2 (7.36) The final task is to vary the parameter k, setting 0, 0 1 2 = ∂ ∂ = ∂ ∂ k W k W The results are that for the ϕ1 (1sa +1sb) function (7.31), the parameter k increases monotonically from 1 to 2 as R decreases from ∝ to 0; for the ϕ2 (1sa -1sb) function (7.32), k decreases monotonically from 1.0 to 0.4 as R decreases from ∝ to 0. Since k is positive and never greater than 2, and since the overlap integral Sab is positive, we see from (7.36) that the resonance integral Hab is always negative. The ground state σg 1s : ab aa ab S H H W + + = 1 1 , ( ) 2 2 1 1 1sa 1sb ab S ϕ φ + φ + = k(Re) = 1.24 Re = 2.02 bohrs, Binding energy: 2.35 eV. (Expt. 2.00 bohrs, 2.79 eV). If we omit varying k, but simply set it equal to 1, we get Re = 2.50 bohrs, Binding energy: 1.76 eV. The excited state σu 1s : ab aa ab S H H W − − = 1 2 , ( ) 2 2 1 2 1sa 1sb ab S ϕ φ −φ − = The appearance of the trial functions for σg 1s and σu 1s
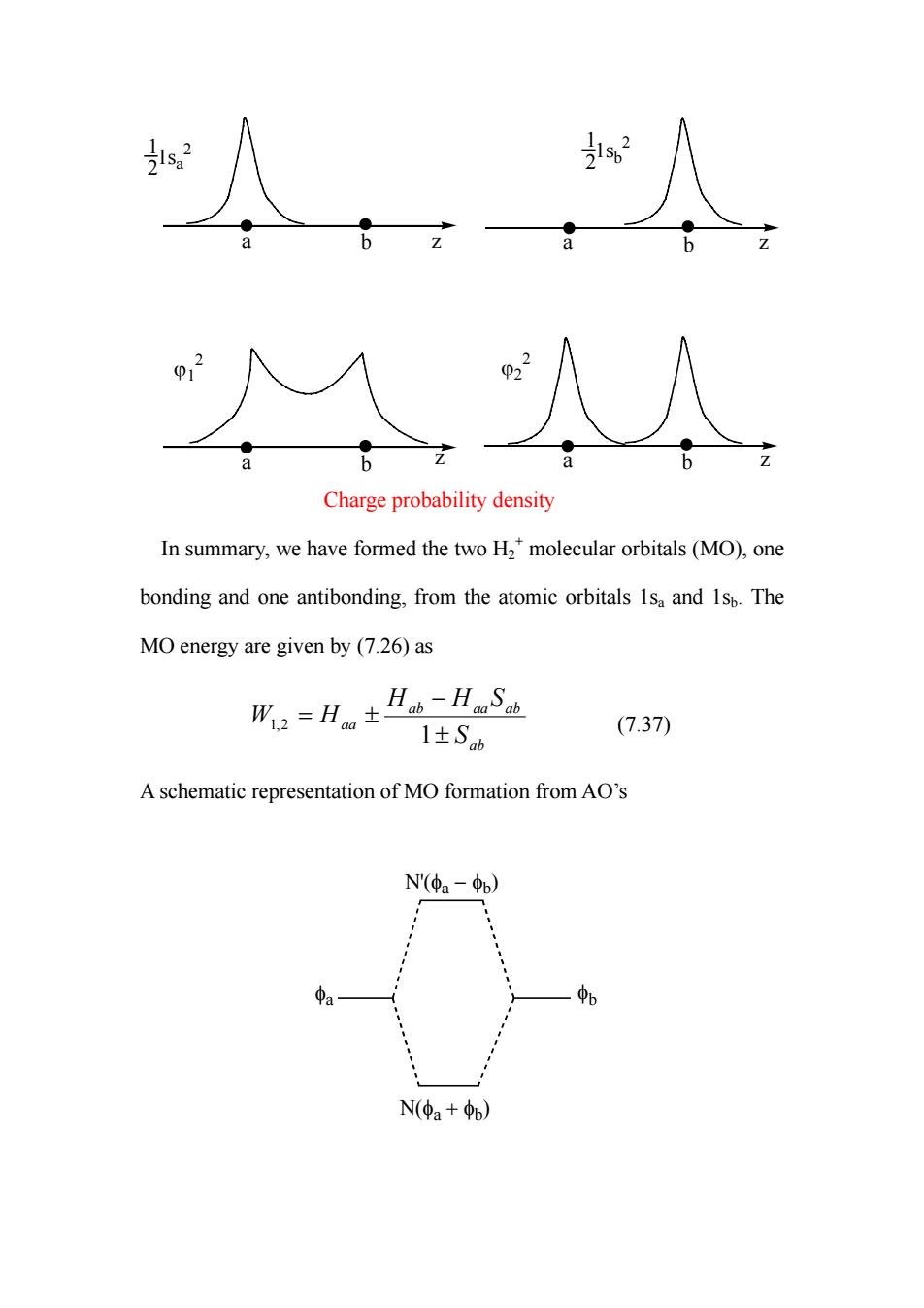
Charge probability density In summary,we have formed the two H2*molecular orbitals(MO),one bonding and one antibonding,from the atomic orbitals Isa and Isp.The MO energy are given by(7.26)as 所2=Hn±h-AS 1±Sb (7.37) A schematic representation of MO formation from AO's Nr(中a-b) N(仲a+b)
. . . . a b a b . . a b . . a b 1sa 1 2 2 1sb 1 2 2 z z z z ϕ1 2 ϕ2 2 Charge probability density In summary, we have formed the two H2 + molecular orbitals (MO), one bonding and one antibonding, from the atomic orbitals 1sa and 1sb. The MO energy are given by (7.26) as ab ab aa ab aa S H H S W H ± − = ± 1 1,2 (7.37) A schematic representation of MO formation from AO’s N'(φa − φb) N(φa + φb) φa φb

Trial function from hybridized AO's(Dickinson in 1933) p=[1s。+c(2p)a]+[1s6+c(2po)b] (7.38) where c is variational parameter,and where 4a=\π (2p)(2p.)cos0. Final results: K=1.246,ξ=2.965,c=0.138 R.=2.01 bohrs,Binding energy:2.73 eV. 3.Molecular Orbitals for H2*Excited States Method of the linear variation function LCAO-MO's C Isa +C22sa +C3(2po)caISs +Cs25p +Co(2po) The symmetry of the homonuclear diatomic molecule makes the coefficients of the atom b orbitals equal to 1 times the corresponding atom a orbital coefficients: p=[G1s。+c22s。+c3(2Po)a]±[G1s6+C22s6+C3(2p)b](7.39) where the upper sign goes with the even(g)states(i.e.+:g;-:u). Relative magnitudes of the coefficients in(7.39) For the electronic states that dissociate into a Is hydrogen atom:Large c Small c2 and c3.As a first approximation,we set c2 and c3 equal to zero, taking
Trial function from hybridized AO’s (Dickinson in 1933) [1 (2 ) ] [1 (2 ) ] a 0 a b p0 b ϕ = s + c p + s + c (7.38) where c is variational parameter, and where a a r a z a kr sa e p p e r k a a θ π ξ π φ ξ cos 4(2 ) , (2 ) (2 ) / 2 1/ 2 5/ 2 0 3 1 − − = = = Final results: K = 1.246, ξ =2.965, c = 0.138 Re = 2.01 bohrs, Binding energy: 2.73 eV. 3. Molecular Orbitals for H2 + Excited States Method of the linear variation function LCAO-MO’s a a a b b p b c 1s c 2s c (2 p ) c 1s c 2s c (2 ) ϕ = 1 + 2 + 3 0 + 4 + 5 + 6 0 The symmetry of the homonuclear diatomic molecule makes the coefficients of the atom b orbitals equal to ±1 times the corresponding atom a orbital coefficients: [ 1 2 (2 ) ] [ 1 2 (2 ) ] 1 a 2 a 3 0 a 1 b 2 b 3 p0 b ϕ = c s + c s + c p ± c s + c s + c (7.39) where the upper sign goes with the even (g) states (i.e. +: g; -: u). Relative magnitudes of the coefficients in (7.39) For the electronic states that dissociate into a 1s hydrogen atom: Large c1, Small c2 and c3. As a first approximation, we set c2 and c3 equal to zero, taking