厦门大学：《群论及其在化学中的应用》课程教学资源（课件讲稿）Chapter 7 Cayley定理 Chapter 8 线性向量空间（Linear vector spaces）Chapter 9 线性算符（Linear Operator）Chapter 10 群的表示

Chapter7 Cayley定理 定理：每个n阶群都与一个n元(n次)置换群Sn的一个子群同构。 设G={80,81,82,…,8m-1} G=n 乘法表：8G=G(重排定理) 80 81828n 81 88088188288m- 8;对应一种重排。 8 8,80881882…8j8m-

Chapter 7 Cayley定理 定理：每个n阶群都与一个n元（n次）置换群 S n 的一个子群同构。 0 1 2 1 { , , , , } 设 G g g g g  n G n  乘法表： g G G i  （重排定理） 0 g 1 g 2 g ┅ n 1 g  i g j g i 0 g g i 1 g g i 2 g g ┅ i n 1 g g  j 0 g g j 1 g g j 2 g g ┅ j n 1 g g  gi 对应一种重排

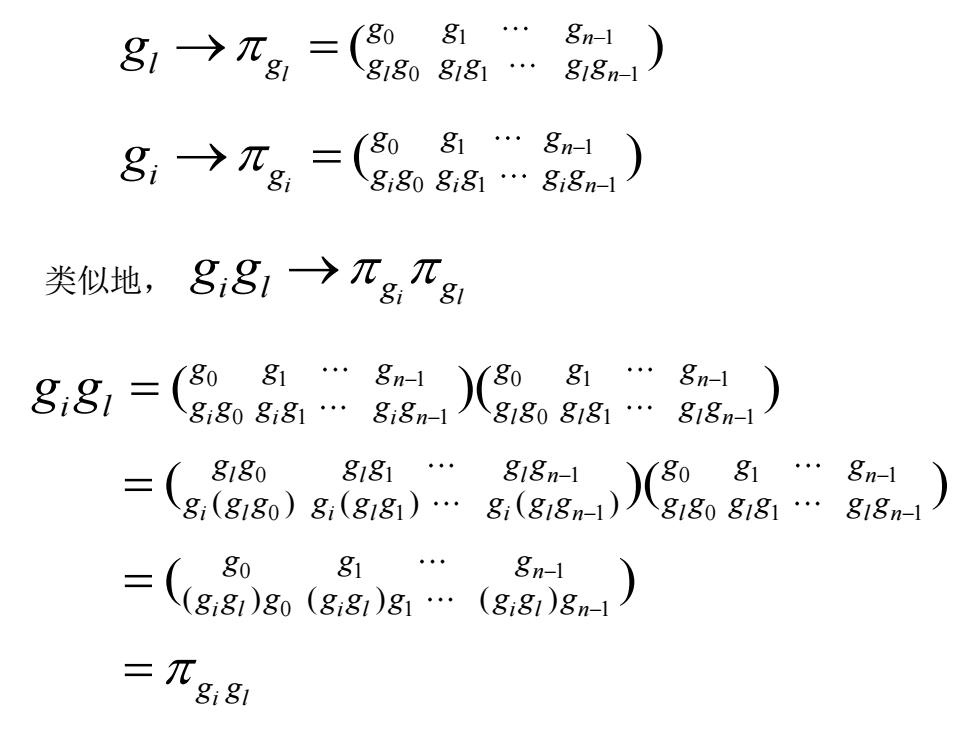
81→πg1 =(80 81… gm-） 81808181· 818n-1 8,-→πg,= 081… 8i808i81…818n-1 类似地， 88→兀grg 881= 8081… 8n-1 8… 8808;81… 8180 8181 … sgg 818n-1 81…8n-1 81(8180）81(8181)… 8081 (g81)g0(g81)g1. 8n-1 (8i81)8n-l = 8187

0 1 1 0 1 1 ( ) n i i i i n g g g i g g g g g g g g      0 1 1 0 1 1 ( ) n l l l l n g g g l g g g g g g g g      0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 0 1 1 ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( )( ) ( ) n n i i i n l l l n l l l n n i l i l i l n l l l n n i l i l i l n i l g g g g g g i l g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g g                类似地， i l i l g g g g  

因此，存在对应关系 81←→πg 81←→πg 881←→πg兀g=πg81 88>πgg=π。e 注意到，{π。，}除π。，所有置换中不存在没有字母不动的 正则置换(Regular Permutation) 由此，有结论：G=n HES,|HFn 由n个正则置换构成的群

因此，存在对应关系 i i g g  l l g g  i l i l i l g g g g g g      1 1 i i i i e g g g g e        注意到， 除 ，所有置换中不存在没有字母不动的 ――正则置换（Regular Permutation） { } i  g  e 由此，有结论： G n  H S  n | | H n  由n个正则置换构成的群

例子：Four-group V群 e a b c e e a b c a a e c b a→πa aecb b bce a c b a e 1234 a 2143 =(12)(34) -g7-05a4 -0 π。=(1)(2)(3)(4) 因此，可以用Cayley定理确定群的可能结构，因为群G(G=n) 与群S,的正则侧置换子群同构(Cayley定理)，而正则置换分解为 循环表示时必须具有相同的循环长度，因此，循环的长度必须是 的因子

例子： Four－group V群 e a b c e a b c e a b c a e c b b c e a c b a e   e a b c a a e c b a    1234 (12)(34) 2143  a         1 2 3 4 (13)(24) 3 4 1 2  b           1 2 3 4 (14)(23) 4 3 2 1  c           (1)(2)(3)(4)  e  因此，可以用Cayley定理确定群的可能结构，因为群G ( ） 与群 的正则置换子群同构（Cayley定理），而正则置换分解为 循环表示时必须具有相同的循环长度，因此，循环的长度必须是n 的因子。 G n  n S

G=4,对应的S4的正则置换子群的长度为4,2 P=(…) P=（…(… 注：这里等循环长度的置换在正则置换群(S,的子群)中不属一 类。 例子G=6 1 23456 ba=a2b go g1 g2 g3 g4 gs ba'=ab e a a2 b ba ba2 go e e a a2 b ba ba? g a a a2 e ba2 b ba a e a ba ba2 b 123456 名 b ba ba2 e a 93 兀a 231645 =(123)(465) ba ba ba2b a2 e g ba2 ba2 b ba a

G  4 ，对应的 S4 的正则置换子群的长度为4，2 4 P  ( ) 4 P ( )( )   注：这里等循环长度的置换在正则置换群（ 的子群）中不属一 类。 例子 n S G  6 1 2 3 4 5 6 g0 g1 g2 g3 g4 g5 e a a 2 b ba ba2 g0 e g1 a g2 a 2 g3 b g4 ba g5 ba2 e a a 2 b ba ba2 a a 2 e ba2 b ba a 2 e a ba ba2 b b ba ba2 e a a 2 ba ba2 b a2 e a ba2 b ba a a2 e ba=a2 b ba2 =ab    123456 123 465 231645  a        

π。→(1)(2)3)(4)(5)(6) π。-→(123)(465) π。-→(132)(456) n个字母的循环n次方等于不动 (单位置换)；正则置换的循 π6→(14)(25)(36) 环结构必须等长。 π→(15)(26)(34) π6m→(16)(24)(35) π=a==e π&=e 习题：对$群进行类分解，确定各类元素的数目， 构造与1G=8群同构的子群

(1)(2)(3)(4)(5)(6)  e  (123)(465)  a  2 (132)(456) a   (14)(25)(36)  b  (15)(26)(34)  ba  2 (16)(24)(35) ba   2 2 2 2 b ba ba       e 3 a   e n个字母的循环n次方等于不动 （单位置换）；正则置换的循 环结构必须等长。 习题： 对S8群进行类分解，确定各类元素的数目， 构造与|G|=8群同构的子群

PartⅡ群的表示理论 Chapter8线性向量空间 (Linear vector spaces) 1.定义 考虑向量集合L={x,y,}，如果 xCL,yCL x+y=y+xCL axcL 实数或复数数域 “加法”或“乘法”满足下列条件 ,B∈K (a+B)x=ax+Bx (aβ)x=a(Bx) 1x=x 则称{x,y,}构成线性矢量空间L。 a(x+y)=ax+ay 0+x=x

Part II 群的表示理论 Chapter 8 线性向量空间 (Linear vector spaces) 1. 定义 考虑向量集合 L { , , } x y ，如果 x y   L L ,  x y y x x      L L “加法”或“乘法”满足下列条件  , K ( ) ( ) ( ) 1 ( ) 0 x x x a x x x x y x y x x                     = + x 则称 { , , } x y 构成线性矢量空间 L 。 实数或复数数域

集合{x,y,}中的元素可以是vectors,points,functions, matrices,--- 若线性矢量空间中最多有n个线性独立的向量，则称L是n维 线性空间。 线性独立，即∑C4≠0，除非C,=0,i=1,…,n 若{4}是线性独立的，有任一向量u m+∑c4-0u=-∑c4 因此，只选n个线性独立的向量{4,2，…，um}作为基或基矢 (向)量。在{u}基下，任意u∈L,可用基展开，即 u=∑xw {4,}：坐标系{x}:称为u的坐标

集合 中的元素可以是 vectors，points，functions， matrices，┅ 若线性矢量空间中最多有 个线性独立的向量，则称 是 维 线性空间。 { , , } x y L 线性独立，即 i i 0 ，除非 i C u  0, 1, , C i n i   若 { } ui 是线性独立的，有任一向量 u 0 i i i u C u    1 2 i i i u C u    因此，只选 个线性独立的向量 作为基或基矢 （向）量。在 基下，任意 ，可用基展开，即 n n 1 2 { , , , }m u u u { }i u uL i i i u x u   { }i u ：坐标系 { }i x ：称为 u 的坐标 n

2.维数：独立向量的个数 0 0 维：卞=a 二维：下=成+b。 三维：产=a成。+b。+c2 球谐函数： 1维： 1=0,s 3维：1=1，Px,Py,P 5维：1=2，dn,d,de,d,dy

2. 维数：独立向量的个数 二维： 0 0 r ax by   三维： 0 0 0 r ax by cz    x y 0 y z x 0 一维： 0 r ax  0 x 球谐函数： 1维： l s  0, 3维： 5维： 1, , , x y z l p p p  2 2 2 - 2, , , , , xy xz yz z x y l d d d d d 

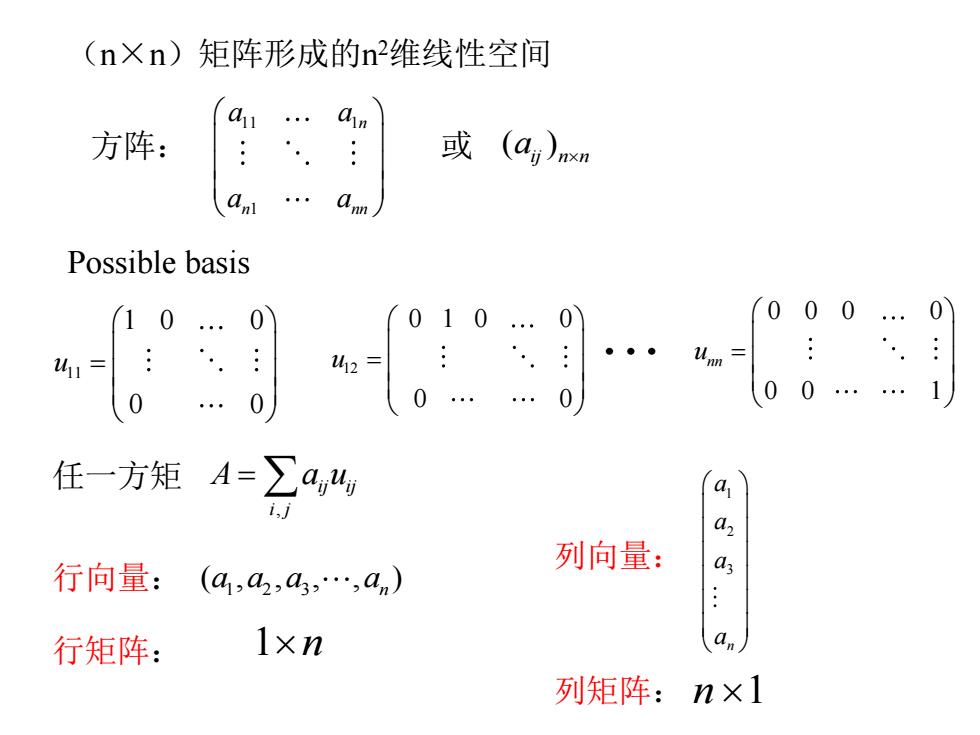
(n×n)矩阵形成的n维线性空间 a 方阵： 或 … Possible basis 10. 0 010..0 (000. 0 411= 412= 0 0 …0 .0 0…… 1 任一方矩A=∑a,4 i 行向量： 列向量： (a1,42,a3,…,an) 行矩阵： 1×n an 列矩阵：n×l

（n×n）矩阵形成的n 2维线性空间 方阵： 11 1 1 n n nn a a a a           或 ( )ij n n a  Possible basis 11 1 0 0 0 0 u            12 0 1 0 0 0 0 u            0 0 0 0 0 0 1 nn u            1 2 3 ( , , , , ) n a a a a 任一方矩 , ij ij i j A a u   行向量： 行矩阵： 1n 列向量： 1 2 3 n a a a a                 列矩阵： n 1