厦门大学：《群论及其在化学中的应用》课程教学资源（课件讲稿）Part I 群论基础 Chapter 1 基本概念 Chapter 2 抽象群的结构

Part I群论基础 Chapter1基本概念 L.群的定义(Group) 设G是一些元素的集合，G={…g}={g}在G中定义了 一种代数运算，称为乘法，记作“。”。如果G对这种运算 满足下面四个条件： 1>闭集合 a·b∈G(一般ab≠ba) 2>结合律a·b·c=(ab)·c=a(b·c) 3>唯一的单位元群中任意的一个元素a有e·a=a·e=a 4>逆元素 对任意a∈G,都可以找到一个元素a∈G使 aa =aa=e 满足上述四个条件的集合(St)G,称为一个群

Part I 群论基础 Chapter 1 基本概念 G { } {}  g g  ab G •  ab ba  1. 群的定义（Group） 设 G 是一些元素的集合， 在 G 中定义了 一种代数运算，称为乘法，记作“• ”。如果 G 对这种运算 满足下面四个条件: 2> 结合律 1> 闭集合 (一般 ) abc ab c a bc •• • • • •  () ()  3> 唯一的单位元 群中任意的一个元素 a 有 ea ae a • •   4> 逆元素 对任意 ，都可以找到一个元素 使 a G -1 a G -1 -1 aa a a e   满足上述四个条件的集合（Set）G，称为一个群

逆元素唯一性的证明： 假设存在另一个逆元素a，则按定义： 同样可以证明： (ab)-1=b-1a1: (ab…hk)-1=k-1h-1..b-1a-1 (ab…hk)-1(ab…hk)=k-h-1.…b-1a-(ab…hk) e=(k-h-1…b-1(a-1a)(b…hk)=(k-h-1.…)(b-b)(…hk)=…=e 群元素的个数称为群的阶(order),记为G。 G有限：有限群：G无限：无限群 离散的无限群：Discrete(infinite)Group. 无限群 Infinite Group L 连续的无限群：Continuous(infinite)Group

逆元素唯一性的证明： 假设存在另一个逆元素a，则按定义： -1 -1 -1 -1 ( ) ( ) a aa a a a aa a a         群元素的个数称为群的阶（order），记为 。 有限：有限群； 无限：无限群 无限群 离散的无限群：Discrete (infinite) Group. 连续的无限群：Continuous (infinite) Group. G G G Infinite Group 同样可以证明： (ab) 1 = b1a 1； (abhk) 1 = k 1h1  b1a 1 (abhk) 1(abhk) = k 1h1  b1a 1(abhk) e = (k 1h1  b1)( a 1a) (bhk)= (k 1h1  ) (b1b) (hk) =  = e

2.同构关系（Isomorphic group) 群的例子： {包，i,1,} 对数的乘法构成一个群 {E,C4,C,C} 乘法：连续转动构成一个群 {E,o};{E,;{E,C2} 抽象群： 二阶群 四阶群 e a a2=e e a a2 a3 ad=e a=0 1i-1-i a=i e C2 a=C2 e i a=i C a=C4

2. 同构关系（Isomorphic group）   2 3 44 4 E,,, CCC 1, , -1, - i i E Ei EC , ; , ; , ...     2 抽象群： 二阶群 ea a2=e e σ a=σ e C2 a=C2 e i a=i eaa2 a3 a4 =e 1 i -1 -i e C4 C43 a=i a=C4 四阶群 对数的乘法构成一个群 群的例子: 2 C4

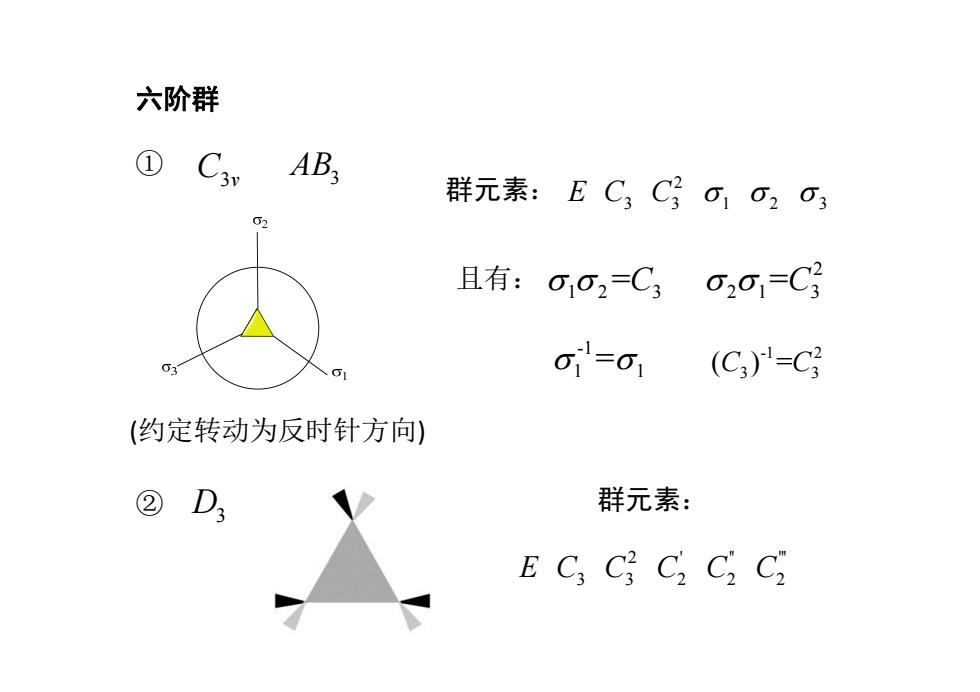
六阶群 ①C3n AB 群元素：EC3CO1O2o3 6 且有：002=C3 0201=C3 01=01 (C3)=C (约定转动为反时针方向) 2 群元素： E C C2 CCC

-1 2 3 3 ( )= C C 2 ' '' ''' EC C C C C 33 222 六阶群 ① C3v AB3 (约定转动为反时针方向) 2 EC C 33 123    12 3  = C 2  21 3 =C -1   1 1 = ② D3 群元素： 群元素： 且有：

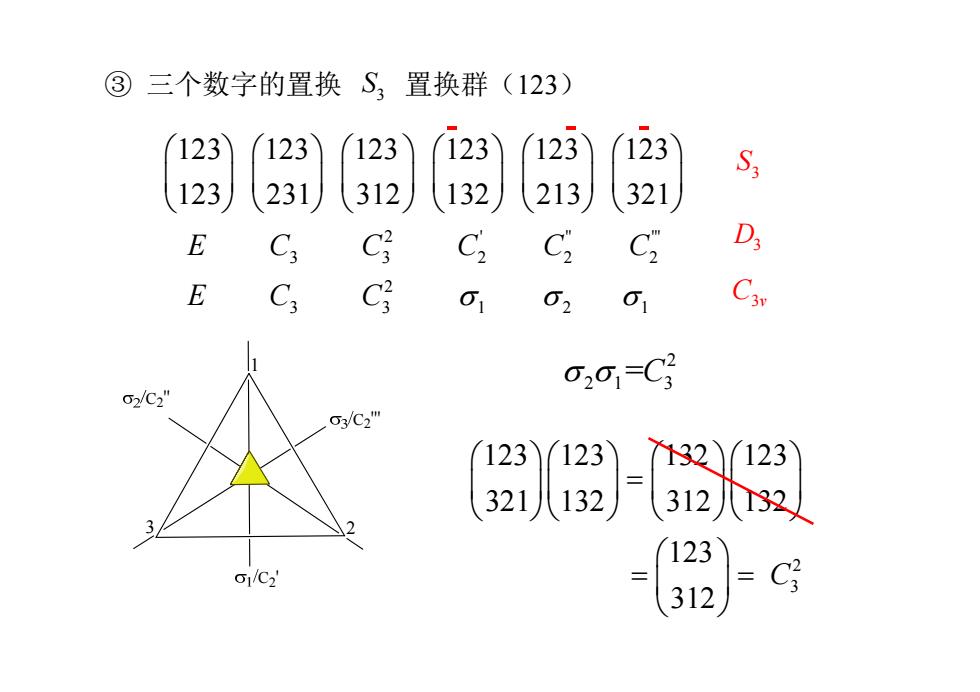
③三个数字的置换S,置换群(123) 123 123 123 123 123 123 231 312 132 213 E C3 C C C C D E C3 C 01 02 01 0201-C 2/C2" O3/C2" 2）-9 o1/C2 a-G

2 ' '' ''' 3 3 222 2 3 3 1 21 123 123 123 123 123 123 123 231 312 132 213 321 E C C CCC EC C                        2 3 123 123 132 123 321 132 312 132 123 312 C                            ③ 三个数字的置换 置换群（ S3 123） 2  21 3 =C C2'' C2' C2''' 1 3 2 3 S D3 C3v

从以上三个六阶群及前面四阶、二阶群的例子有： F 8,→f8,→f88,→f∫ gi 称G与F群同构。 上述六阶群的抽象群形式： a b ab ab (a3=eb2=e) C3v E C3 C oi 02 03 D E C c C C, 123 123 123 123 123 123 123 231 312 132 321 213 同构群具有相同的性质。因此，对上述六阶抽象群的研究便可以获得 其它类似群（具体形式）的性质

从以上三个六阶群及前面四阶、二阶群的例子有： ... i i j j i j ij g f g f gg f f    g 0 gi gj gi-1 f0 fi fj fi-1 G F 上述六阶群的抽象群形式： 2 23 2 2 3 3 3 1 23 2 ' '' ''' 3 3 3 2 22 3 123 12 123 ( ) v e a a b ab a b a e b e CE C C DE C C C CC S           3 123 123 123 123 231 312 132 321 213                   同构群具有相同的性质 。因此，对上述六阶抽象群的研究便可以获得 其它类似群（具体形式）的性质。 称 G 与 F群同构

3.子群(Subgroup) G是一个群，如果G的一个子集H对G的运算构成一个群， 则称H是G的一个子群。 {e},{g}=G为平凡子群 :--trivial subgroup HCG 真子群一一proper subgroup G={8o,g1,,8m1}G=n 子集H={h,h,,h.}H=k HCG且{h子集元素满足G的结合律等群的条件。 例如：C:{E,C,C,o,o,o} CC3=CC3=E {EC,C}3阶真子群 {E,o}2阶真子群

3. 子群（Subgroup） H G  G  gg g 0 1 -1 , , ..., n  G n  H hh h H k    0 1 -1 , , ..., k    2 3 33 123 : , , , , , C EC C v    2 2 CC CC E 33 3 3   E,  G 是一个群，如果 G 的一个子集 H 对 G 的运算构成一个群， 则称 H 是 G 的一个子群。 { },{ } e g  G 为平凡子群 ――trivial subgroup H G  真子群――proper subgroup 子集 且{h}子集元素满足 G 的结合律等群的条件。 例如：   2 3 3 EC C , , 3阶真子群 2阶真子群

判别方法1 充分必要条件 ①如果a,b∈H,则abeH。 ②如果aeH,则a∈H。 证明：上述条件显然是必要的。为证明充分条件，只需证明 e∈H就行了。 取a∈H,由②有a∈H,由①有aa=e∈H。 判别方法2 充分必要条件 如果a,b∈H,则ab∈H。 取a∈H,则aa'=e∈H,又有ea1=a∈H,即b∈H a(b-l)=ab∈H 故H是G的子群

判别方法 1 充分必要条件 ① 如果 ，则 。 , ab H  ab H  ② 如果 ，则 。 a H  -1 a H  证明：上述条件显然是必要的。为证明充分条件，只需证明 e H  就行了。 取 ，由②有 ，由①有 。 a H  -1 a H  -1 aa e H   判别方法 2 充分必要条件 -1 如果 ，则 。 , ab H  ab H  取 ，则 ，又有 ，即 a H  -1 aa e H   -1 -1 ea a H   -1 b H  -1 -1 a b ab H ( )   故 H 是 G 的子群

4.循环子群（Cyclic Subgroup) 如果群G中有 al=am,al-m=e,1-m=k ak-e 把元素α所有幂组合起来，构成一个循环子群。 k叫做a的阶，a称为循环子群的生成元(generator) e.a.aala=e k阶循环子群 例子：C3x{E,C3,C3,0,0,o} 三阶循环子群：{E,C,C} 二阶循环子群：{E,o} 每一个群一定存在一个循环子群

4. 循环子群（Cyclic Subgroup） 如果群 G 中有  , , l m lm k a a a e lmk a e      把元素 a 所有幂组合起来，构成一个循环子群。 k 叫做 a 的阶，a 称为循环子群的生成元（generator）   2 1 , , ,..., k k eaa a a e  |  k 阶循环子群 例子：   2 3 33 123 : ,, ,,, C EC C v     2 3 3 三阶循环子群： 二阶循环子群： EC C , , E, 每一个群一定存在一个循环子群

Chapter2抽象群的结构 1.群的乘法表(Group Table)) G={g0,g1,,g1),ggn-} G=n 80 81 82 8 8 … 8n-1 80 81 8k 880881882…881…88 88n-1 8 gn-1 表中任一列或任一行元素不存在相同的，只是所有群元素的 重新排列—重排定理

g0 g1 g2 … gi … gj … gn-1 g0 g1 ⁞ gk gkg0 gkg1 gkg2 … gkgi … gkgj gkgn-1 ⁞ gj ⁞ gn-1 Chapter 2 抽象群的结构 表中任一列或任一行元素不存在相同的，只是所有群元素的 重新排列——重排定理 1. 群的乘法表 (Group Table) G = { g0, g1, …, gi, …, gj, gn-1} |G|=n