
Chapter9多原子的半经验方法 1.n-electron approximation 2.The free-electron MO method 3.The Huckel MO method 4.Conjugated Chain Molecules 5.Monocyclic Conjugated Polyenes 6.Polycyclic Conjugated Polyenes 7.Charges,Bond Orders and Free Valences 8.General Semi-empirical MO Methods
Chapter 9 多原子的半经验方法 1. π- electron approximation 2. The free-electron MO method 3. The Huckel MO method 4. Conjugated Chain Molecules 5. Monocyclic Conjugated Polyenes 6. Polycyclic Conjugated Polyenes 7. Charges, Bond Orders and Free Valences 8. General Semi-empirical MO Methods

1.n-electron approximation (1) i=i>i ri core (2) V(①:第i个π电子在核与电子场中的势能, 由变分原理,极小化变分积 imfp,H.p.dr)={E:p》
1. π-electron approximation 1 1 1 core ^ ^ i i j i ij n n H H ( i ) r = = = + 1 2 2 core ^ H i V( i ) = − + (1) (2) 由变分原理, 极小化变分积 V(i):第i个π电子在核与电子场中的势能. ^ * Min( d ) , H E

2 The free-electron MO method 1 如果:忽略, 且 V=0, in a certain region outside this region 有:H.p.=E.0 (3) o.-i9 (4) core H.(=e (5)
2 .The free-electron MO method V= , outside this region 如果: 忽略, 且 V=0, in a certain region 1 rij 有: ^ H E = i i n = (3) (4) ^ i i i H ( ) e core i = (5)

E.- e (6) 维情况,有 e- h' m. n,=1,2…(7) 由Paui原理,有: 2 HOMO-LUMO Excitation
i i 1 n E e = = (6) 一维情况,有 2 2 i i 2 i , 1,2,...... 8 h n m l e n e = = (7) 由Pauli 原理,有: ... 1 2 3 4 ... 1 2 3 4 HOMO-LUMO Excitation

AE=m=es-en⅓=hn% 2egcyn7n.+ (8) 对于Polyenes: 设单键长,1,双键长,2,考虑MOs离域,两端分别增加 1+ 则电子运动的区域: 息++g++=0-+60 2 =2k+30+4)=22k+2+10+4 =2(n.+100+4)
n 1 2 2 E hc hv e e n + = = − = (8) 1 n 2 2 2 e 1 1 ( ) ( 1) 8 e e n n h hc m l C + = − = + 对于Polyenes: 设单键长, l1 , 双键长, l2 , 考虑MOs离域, 两端分别增加 1 2 . 则电子运动的区域: 3 1 4 4 l l + 1 2 1 2 1 2 1 2 1 2 1 2 3 1 3 ( 1) ( )( ) 2 2 2 1 1 (2 3)( ) (2 2 1)( ) 2 2 1 ( 1)( ) 2 c kl k l l l l l l k l l k l l n l l + + + + = + + = + + = + + + = + +

代入(8)式有: =2mch'(L+12)2(n。+1)=(n。+1(64.6m) 3.The Huckel MO method Ha-H () H (g,=ep (12) -2f (13) 由线性变分法有:
代入(8)式有: 1 2 1 2 2 ( ) ( 1) ( 1)(64.6 ) m ch l l n n nm e c c − = + + = + 3 . The Huckel MO method ^ ^ ( ) eff i n H H i = (11) 1 c ri i r r n c f = = ^ ( ) eff i i i H i = e (12) (13) 由线性变分法有:

2H-s-e)c.1=0=1,23…n (14 久期方程 det H-s,e,=0 (15) 积分 H=∫fr)H)f),≡a (16) Hf(H()f (i)dv,=B for C &C,bonded =0 for CC,not bonded together (17 sn=∫f,0f,0)本=δ (18)
1 [( ) ] 0 c eff rs rs i si s n H sec = − = r=1,2,3,….nc (14) 久期方程: det | | 0 eff H S e rs rs i − = (15) 积分 * ( ) ( ) ( ) eff eff H f i H i f i dv rr r r i = ^ * ( ) ( ) ( ) eff eff i rs r r H H = f f i i i dv for Cr & Cs bonded (16) 0 eff H rs = for Cr & Cs not bonded together * ( ) ( ) i rs rs r s f f i i dv s = = (17) (18)

f≡C,2p. (19) 归一化条件(normalization condition) leaf =1 (20) 4.Conjugated Chain Molecules 1234n C-C-C-C..C (21)
2 r r f C p 归一化条件(normalization condition ) (19) 2 1 c ri r s n c = = (20) 4. Conjugated Chain Molecules 1 2 3 4 ... n c c c c c −−− (21)
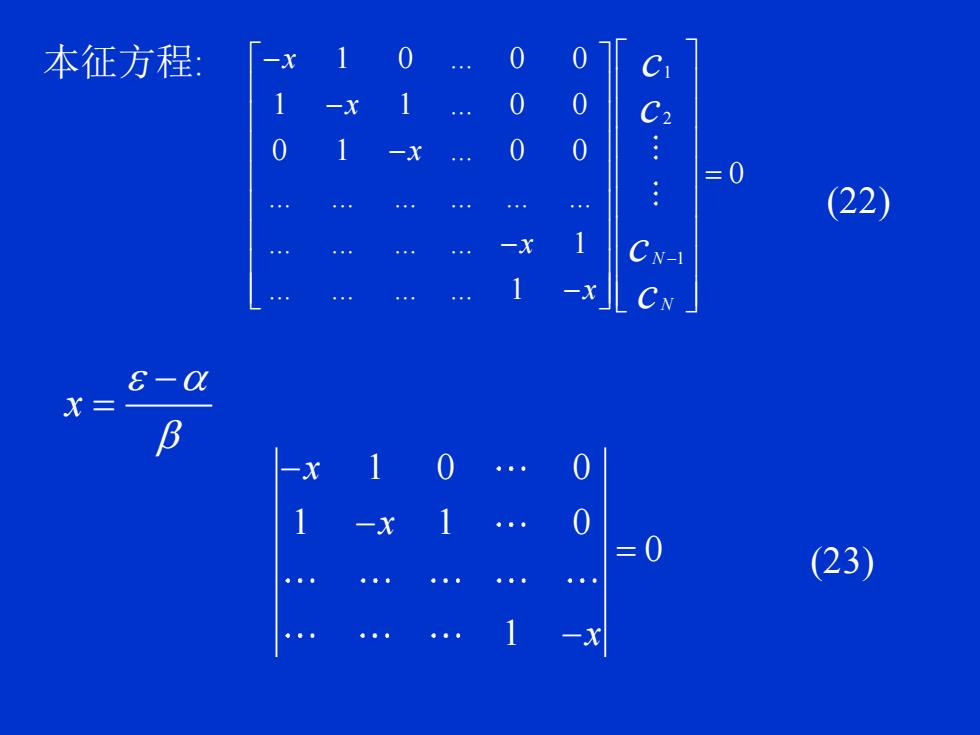
本征方程 0 C 1 0 0 一X 0 .: (22) CN- CN 8-Q X= 一X 0 (23)
本征方程: 1 2 1 1 0 ... 0 0 1 1 ... 0 0 0 1 ... 0 0 0 ... ... ... ... ... ... ... ... ... ... 1 ... ... ... ... 1 N N x x x x x c c c c − − − − = − − (22) x − = 1 0 0 1 1 0 0 1 x x x − − = − (23)

由行列式理论有 Ek=a+xB kπ (24) X=2cos N+1 k=1,2,3,,N 2 kuπ CN+1 in k=1,2,3,,N N+1 u=1,2,3,,N (25) 123 4 例子:丁二烯 H,C=C-C=CH, 2π X=2cos π X2=2cos 5 (26) 3π An X;=2cos X=2cos 5 5
由行列式理论有: k = + k 2cos 1 k k N x = + k=1, 2, 3, …, N (24) 2 sin 1 1 uk ku N N c = + + k=1, 2, 3, …, N u=1, 2, 3, …, N (25) 例子:丁二烯 1 2 3 4 H C C C C H 2 2 = − = 1 2cos 5 x = 3 3 2cos 5 x = 2 2 2cos 5 x = 4 4 2cos 5 x = (26)