(2)复因子试验 1、橡胶树品系A与栽培密度B试验,采用随机区组设计重复4次,测得小区年 业加下岁.式求出 S8.SSx(供10分) 处理组合 A2 区组和 区组 B2B3 B2 B3 区组1 56 6066 65 60 53360 区组2 45 5057 61 58 53324 区组3 43 455060 56 48 302 区组4 46 485063 60 55322 处理总和190203223249234 209T=1308 解: a62x3x47186 13082 -c=1902+2032+.+2092 -c=583 4 , -c=6162+692 -c=240.67 bn 3×4 -c=4392+4372+432 -c=3.25 an 2×4 55B=5S处理一5SA-5SB=339.08 2.试对下表资料进行方差分析,要注求出各因子主效应及交互作用的F值(数 据已简化,资料不需代换)。(15分) A2 区组和 因子 Bl B2 B3 B2 B3 区组 11 1521 20 15 8 90 区组2 0 5 12 16 13 8 54 区组3 -2 05 15 11 3 32 处理总和 9 2038 51 39 19 176 答案:
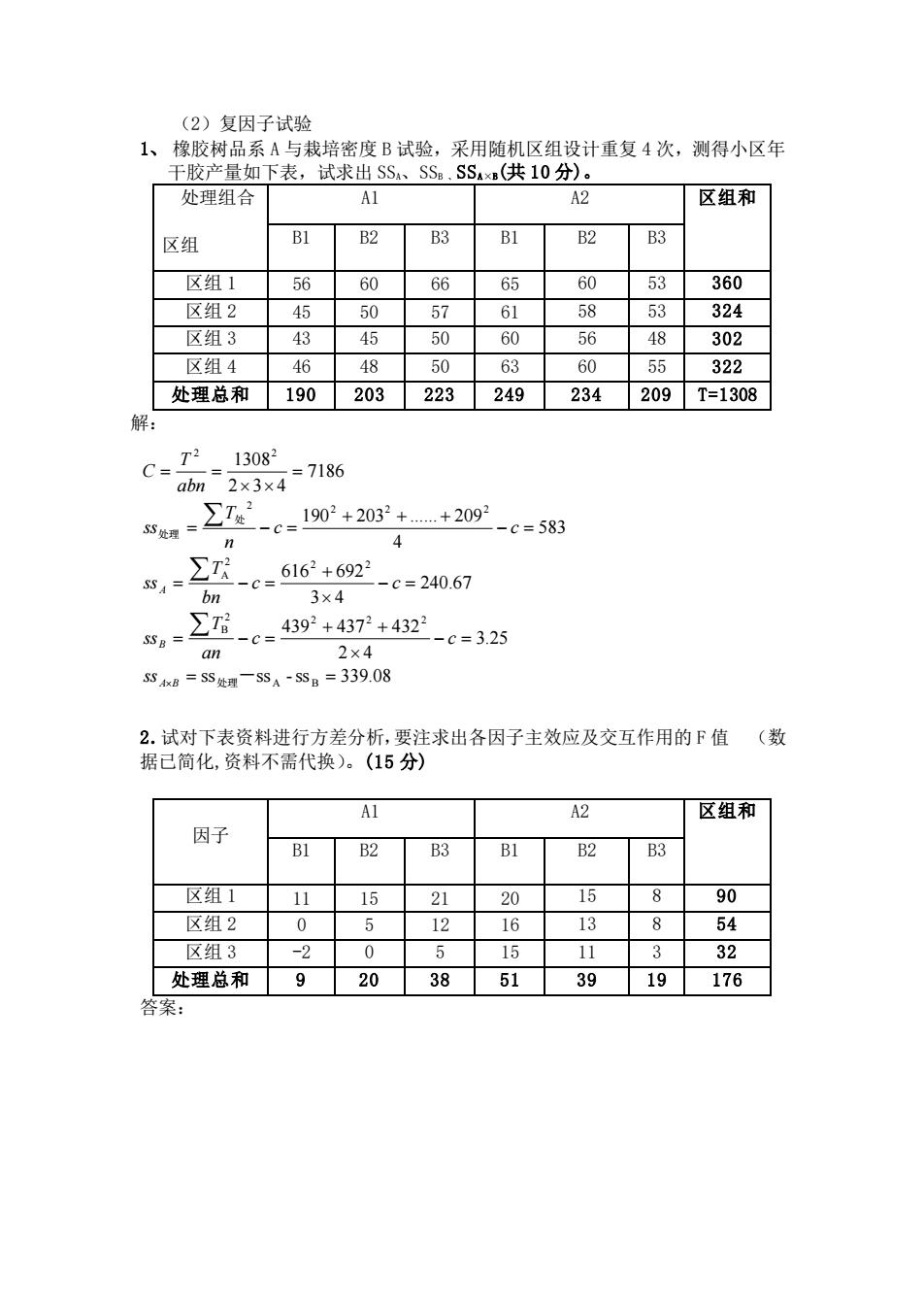
(2)复因子试验 1、 橡胶树品系 A 与栽培密度 B 试验,采用随机区组设计重复 4 次,测得小区年 干胶产量如下表,试求出 SSA、SSB 、SSA×B(共 10 分)。 处理组合 区组 A1 A2 区组和 B1 B2 B3 B1 B2 B3 区组 1 56 60 66 65 60 53 360 区组 2 45 50 57 61 58 53 324 区组 3 43 45 50 60 56 48 302 区组 4 46 48 50 63 60 55 322 处理总和 190 203 223 249 234 209 T=1308 解: ss ss -ss 339.08 3.25 2 4 439 437 432 240.67 3 4 616 692 583 4 190 203 . 209 7186 2 3 4 1308 A B 2 2 2 2 B 2 2 2 A 2 2 2 2 2 2 = = − = + + = − = − = + = − = − = + + + = − = = = = 处理- 处 处理 A B B A ss c c an T ss c c bn T ss c c n T ss abn T C 2.试对下表资料进行方差分析,要注求出各因子主效应及交互作用的 F 值 (数 据已简化,资料不需代换)。(15 分) 因子 A1 A2 区组和 B1 B2 B3 B1 B2 B3 区组 1 11 15 21 20 15 8 90 区组 2 0 5 12 16 13 8 54 区组 3 -2 0 5 15 11 3 32 处理总和 9 20 38 51 39 19 176 答案:
C= 1762 Mm-2x3x3=1720,89 5S。=∑∑x2-c=2518-c=797.11 -c=902+54+32 -c=285.78 ab 2×3 -c=92+202+.+192 -c=415.11 SS=797.11-285.78-415.11=96.22 -c=672+1092 -c=9800 bn 3×3 -c-602+592+57 -c=0.78 an 2×3 5B=5St-s54-55B=415.11-98.00-0.78=316.33 变异来源自由度SS S 区组 2 285. 78 142. 89 98.00 98.00 10.18 0.78 0.39 0.041 AXB 316.33 158.16516.44 误差 10 96.22 9.622 总变异■ 17 797.11 46.89 (10分)试对下表资料进行方差分析,要注求出各因子主效应平方和(数据已简 化,资料不需代换)。 A2 区组和 因子 B2 B3 BI B2 B3 区组1 11 1521 20 15 890 区组2 0 512 16 13 8 54 区组3 -2 05 15 11 32 处理总和 9 2038 51 39 19 176 解 176 abm2x3x3=1720.89 -c=672+109 -c=98.00 bn 3×3 ,= -c=602+692+57 -c=214.11 an 2×3
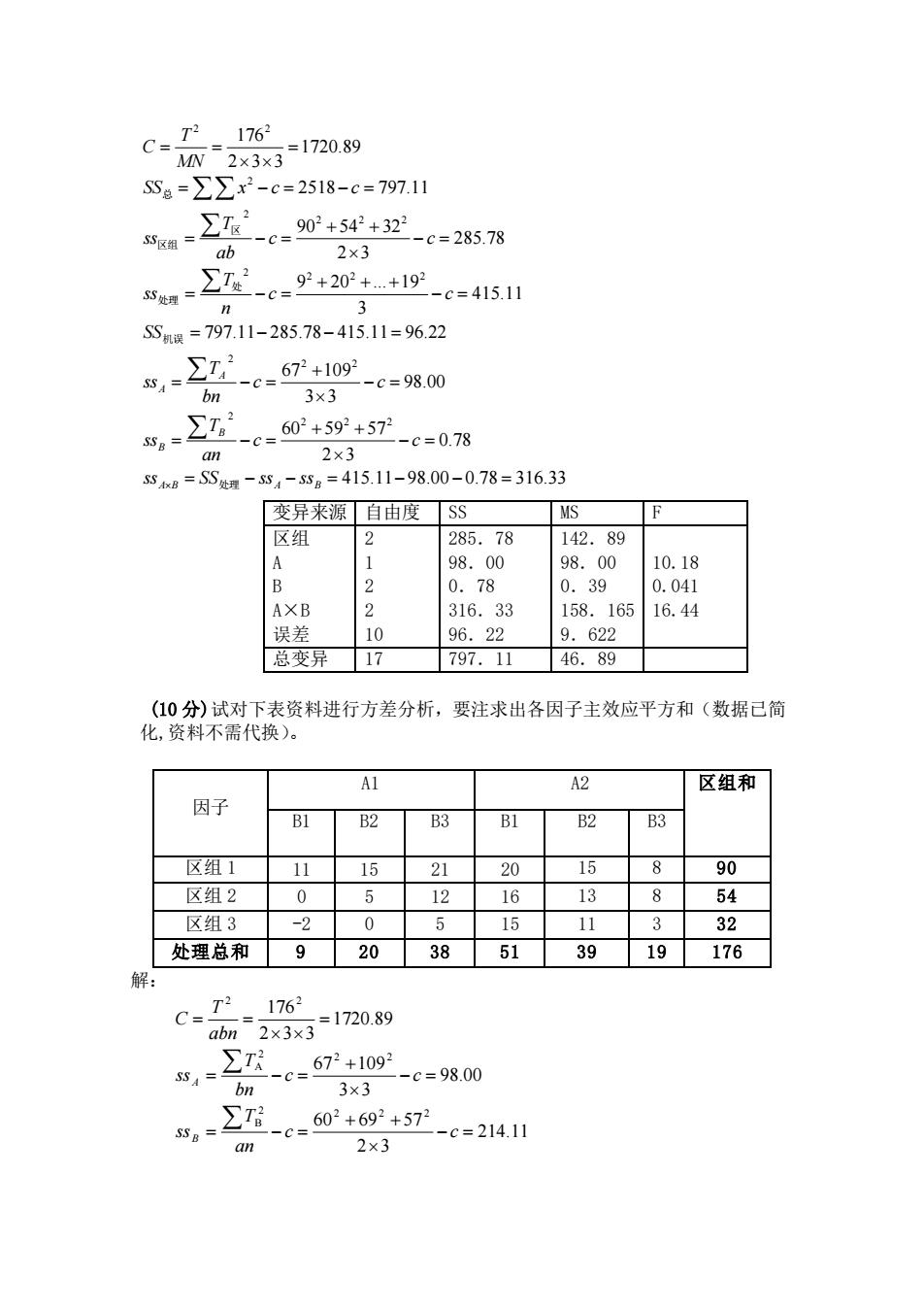
415.11 98.00 0.78 316.33 0.78 2 3 60 59 57 98.00 3 3 67 109 797.11 285.78 415.11 96.22 415.11 3 9 20 . 19 285.78 2 3 90 54 32 2518 797.11 1720.89 2 3 3 176 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 = − − = − − = − = + + = − = − = + = − = = − − = − = + + + = − = − = + + = − = = − = − = = = = A B A B B B A A ss SS ss ss c c an T ss c c bn T ss SS c c n T ss c c ab T ss SS x c c MN T C 处理 机误 处 处理 区 区组 总 变异来源 自由度 SS MS F 区组 A B A×B 误差 2 1 2 2 10 285.78 98.00 0.78 316.33 96.22 142.89 98.00 0.39 158.165 9.622 10.18 0.041 16.44 总变异 17 797.11 46.89 (10 分)试对下表资料进行方差分析,要注求出各因子主效应平方和(数据已简 化,资料不需代换)。 因子 A1 A2 区组和 B1 B2 B3 B1 B2 B3 区组 1 11 15 21 20 15 8 90 区组 2 0 5 12 16 13 8 54 区组 3 -2 0 5 15 11 3 32 处理总和 9 20 38 51 39 19 176 解: 214.11 2 3 60 69 57 98.00 3 3 67 109 1720.89 2 3 3 176 2 2 2 2 B 2 2 2 A 2 2 − = + + = − = − = + = − = = = = c c an T ss c c bn T ss abn T C B A

2复因子试验,采用随机区组设计重复三次,试验结果如下(可量 资料): 处理组合|A1BI AIB2 A2BI |A2B21 |区组 人 112 1315 2131415 Ⅲ1233 1合计14 17110113 试用二向表求N平方和。 |W|W1W2|N项统计 IN I T T 1014196 N27 13120400 34596 C=T/(4×3)=34/12=96.3 SSN=596/(2X3)-C=3.03 T 34 C= = =96.3 m n 3×4 ∑Tn 596 -C= 96.3=3.03 Nw水平数X区组数 2X3 2复因子试验,采用随机区组设计,重复三次,试验结果如下: (可量资料)试求各因子的平方和。 处理A1B1A1B2|A2B1|A2B2 区组 1111315111 11101214121 11114121015 1合计151719181
2 复因子试验,采用随机区组设计重复三次,试验结果如下(可量 资料): ┌──────┬────┬────┬────┬────┐ │ 处理组合│A1B1 A1B2 │A2B1 │A2B2 │ │区组 │ │ │ │ │ ├──────┼────┼────┼────┼────┤ │ I │ 1 │ 2 │ 3 │ 5 │ ├──────┼────┼────┼────┼────┤ │ II │ 2 │ 3 │ 4 │ 5 │ ├──────┼────┼────┼────┼────┤ │ III │ 1 │ 2 │ 3 │ 3 │ ├──────┼────┼────┼────┼────┤ │ 合 计 │ 4 │ 7 │ 10 │ 13 │ └──────┴────┴────┴────┴────┘ 试用二向表求N平方和。 ┌──┬────────┬────────┐ │ W│ W1 W2 │ N项统计 │ │N │ │ T T │ ├──┼────────┼────────┤ │N1│ 4 10 │14 196 │ │N2│ 7 13 │20 400 │ ├──┴────────┴────────┤ │ 34 596 │ └────────────────────┘ C=T /(4×3)=34 /12=96.3 SSN=596/(2×3)-C=3.03 T 34 C= ─── = ─── =96.3 mn 3×4 ∑Tn 596 SS =──────── -C=────-96.3=3.03 N w水平数×区组数 2×3 2 复因子试验,采用随机区组设计,重复三次,试验结果如下: (可量资料)试求各因子的平方和。 ┌─────┬──┬──┬──┬──┐ │ 处理 │A1B1│A1B2│A2B1│A2B2│ │区组 │ │ │ │ │ ├─────┼──┼──┼──┼──┤ │ I │1 │3 │5 │1 │ │ II │0 │2 │4 │2 │ │ III │4 │2 │0 │5 │ ├─────┼──┼──┼──┼──┤ │ 合 计 │5 │7 │9 │8 │ └─────┴──┴──┴──┴──┘

A2 T 1B115 9 114196106 1B217 815225113 l t 112 1712g 421219 IT 11442891433 C=T/(4×3)=29/12=70.08 SSA=433/(2×3)-C=2.09 ssB=421/(2×3)-C=0.09 29 C= =70.08 m n 3X4 -C AB水平数×区组数 433 = -70.08=2.09 2×3 ETb SS = BA水平数X区组数 421 -70.08=0.09 2×3
┌──┬────────┬──────────┐ │ A│ A1 A2 │ T T ΣX │ │B │ │ │ ├──┼────────┼──────────┤ │B1│ 5 9 │14 196 106│ │B2│ 7 8 │15 225 113│ ├──┼────────┼──────────┤ │ T │ 12 17 │29 421 219│ │T │ 144 289│433 │ └──┴────────┴──────────┘ C=T /(4×3)=29 /12=70.08 SSA=433/(2×3)-C=2.09 SSB=421/(2×3)-C=0.09 T 29 C= ─── =──── =70.08 mn 3×4 ∑Ta SS =──────── -C A B水平数×区组数 433 = ─── -70.08=2.09 2×3 ∑Tb SS =──────── -C B A水平数×区组数 421 = ─── -70.08=0.09 2×3