
生物统计学试题库 五 一、解释以下术语及符号 20分 样本统计量 偶然误差 处理 重复 生物统计学 小机率原理 SS LSDo. b 二、填空题20分 1因试验环境的趋势性变异而导致的误差称为: ,因试验环境 的随机性变异而导致的误差称为: ,试验设计的目标是避免 误差,缩小 误差。 2主效应是一个因子的 之间, 的平均差异。 3L,(3)表示一张个横行个列的正交表。如采用该正交表安排试 验,则试验处理数为个。 4点估计是指用 去估计集团平均数;而区间估计是指在规定的
1 生物统计学试题库 五 一、解释以下术语及符号 20 分 样本统计量 偶然误差 处理 重复 生物统计学 小机率原理 SS Sy LSD0.05 b 二、填空题 20 分 1 因试验环境的趋势性变异而导致的误差称为: ,因试验环境 的随机性变异而导致的误差称为: ,试验设计的目标是避免 误差,缩小 误差。 2 主效应是一个因子的 之间, 的平均差异。 3 L9(3 4 )表示一张个 横行 个列的正交表。如采用该正交表安排试 验,则试验处理数为 个。 4 点估计是指用 去估计集团平均数;而区间估计是指在规定的

下估计集团平均数的 和 5 的资料可用t测验法进行显著性分析,而 的资料则可用卡平方测验法进行显著性分 析,测验一个未知比例是否与一个已知比例相符作卡平方的 测验、 测验2个(或多个)未知此例是否相符作卡平方的 6方差分析时,对各处理两两间进行多重比较的常用方法有: 等 三、简答题10分 1请说明单因子试验三种方法各自的适用范围。 2请分别解释统计假设μA=μB=.=μM成立与不成立的统计意义。 四、问答题10分 1请简述本课程中所学过的统计假设测验、方差分析、直线相关与回归分析等 这三种统计分析方法在作用上的区别。 五、计算题40分 1、现对幼苗高度进行测定得数据:9,7,10,8,11,10,12,10,8,10, 11(单位:cm),请计算此资料的平均数、平方和、标准差、变异系数、 标准误,并求其置信度为95%的区间。to.6,2.306;ta.6=2.262: t0.0610=2.228: 2、 用随机区组法安排A、B两个处理进行比较试验,试分析不同处理间产量 是否存在显著差异。to.s=2.262to.1=3.25
2 下估计集团平均数的 和 。 5 的资料可用 t 测验法进行显著性分析,而 的资料则可用卡平方测验法进行显著性分 析,测验一个未知比例是否与一个已知比例相符作卡平方的 测验、 测验 2 个(或多个)未知比例是否相符作卡平方的 6 方差分析时,对各处理两两间进行多重比较的常用方法有: 、 、 等 三、简答题 10 分 1 请说明单因子试验三种方法各自的适用范围。 2 请分别解释统计假设 μA=μB=.=μM 成立与不成立的统计意义。 四、问答题 10 分 1 请简述本课程中所学过的统计假设测验、方差分析、直线相关与回归分析等 这三种统计分析方法在作用上的区别。 五、计算题 40 分 1、 现对幼苗高度进行测定得数据:9,7,10,8,11,10,12,10,8,10, 11 (单位:cm),请计算此资料的平均数、平方和、标准差、变异系数、 标 准误,并 求其置信 度为 95% 的区 间。t0.05,8=2.306; t0.05,9=2.262; t0 .05,10=2.228; 2、 用随机区组法安排 A、B 两个处理进行比较试验,试分析不同处理间产量 是否存在显著差异。t0.05=2.262 t0.01=3.25
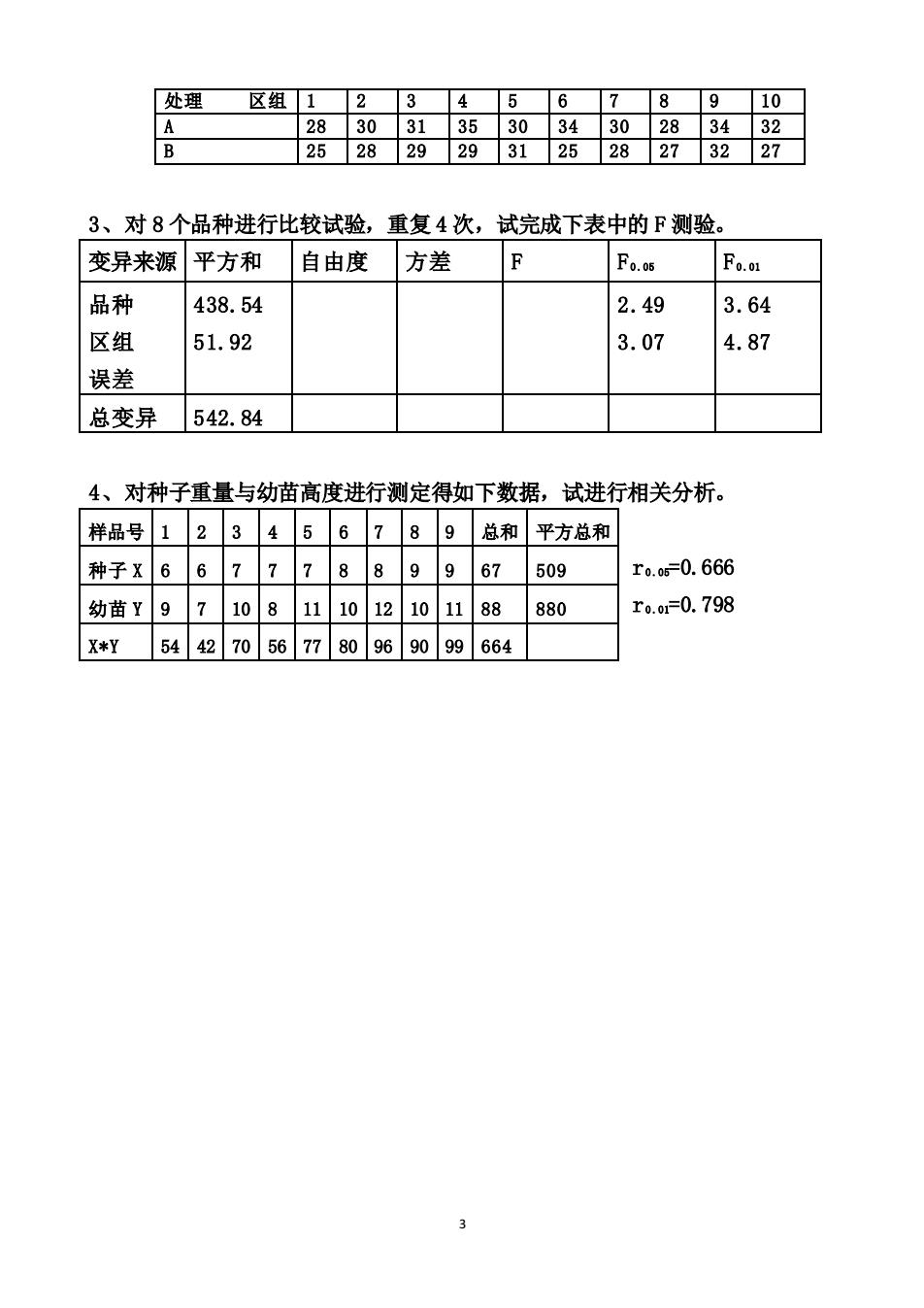
处理区组12345678910 28303135303430283432 B 25282929312528273227 3、对8个品种进行比较试验,重复4次,试完成下表中的F测验 变异来源平方和 自由度 方差 Fo.os F0.o1 品种 438.54 2.49 3.64 区组 51.92 3.07 4.87 误差 总变异542.84 4、对种子重量与幼苗高度进行测定得如下数据,试进行相关分析。 样品号123456789总和平方总和 种子x66777889967509 ro.6=0.666 幼苗Y97108111012101188880 ro.o1=0.798 X*y544270567780969099664 3
3 处理 区组 1 2 3 4 5 6 7 8 9 10 A 28 30 31 35 30 34 30 28 34 32 B 25 28 29 29 31 25 28 27 32 27 3、对 8 个品种进行比较试验,重复 4 次,试完成下表中的 F 测验。 变异来源 平方和 自由度 方差 F F0 .05 F0 .01 品种 区组 误差 438.54 51.92 2.49 3.07 3.64 4.87 总变异 542.84 4、对种子重量与幼苗高度进行测定得如下数据,试进行相关分析。 r0 .05=0.666 r0 .01=0.798 样品号 1 2 3 4 5 6 7 8 9 总和 平方总和 种子 X 6 6 7 7 7 8 8 9 9 67 509 幼苗 Y 9 7 10 8 11 10 12 10 11 88 880 X*Y 54 42 70 56 77 80 96 90 99 664

参考答案 一、解释以下术语及符号(其中符号解释需要写出名称、公式、含义与作用) 1.样本统计量::指由样本的全部观察值而算得的样本特征数。 2.偶然误差(机误):由于机会不等所造成的偏差。或在试验中由不确定的因数而引起的误 差,具随机性。 3.处理:指事先设计好的实施在试验单位上的一种具体措施或试验中的具体比较项目叫做处 理。 4.重复:每个品种(或处理)占有两个或两个以上的小区称有重复。 5.生物统计学:是数理统计的原理和方法在生物科学研究中的应用,是一门应用数学。 6.小机率原理:概率很小的事件,在一次试验中是不至于发生的。 7.SS:平方和,反应资料的总变异。 8.Sy:标准误,估计抽样误差。 9.LSD.s:显著水准为0.05的最小显著差数的临界值。 10.b:样本的直线回归系数,反映当x每变化1个单位时y的理论变化量。 二、填空题 评分标准:填写正确的数学符号也同样得分 1系统误差,偶然误差(或随机误差),系统误差,偶然误差(或随机误差)。 2各个水平,各个简单效应。 39.4.9。 4样本平均数:可信度(或显著水平),上限、下限。 5单个或两个样本可量(或连续性变数),单个或两个样本计数性(或非连续性变数),适 合性、独立性」 6LSD法、SSR法和q法。 三、简答题 2答: 完全随机设计:试验空间中的各种非试验因素者相当均匀一致的实验条件。一般仅在实 验室试验,温室试验或处理虽多但每处理材料甚少的田间试验中应用。 随机区组设计:适合于有一个方向明显误差的,处理数限于18个以内的单、复因子试验, 实施单方面局部控制原则,应用最广泛。 拉丁方设计:适合于有两个明显误差的试验,实施双方面局部控制,处理数限于5-8个 2答:若HO:μ=μ=.=μ,成立,根据小概率原理,则接受统计假设HO,否定H, 样本A、B,.,M处理的平均数无显著差异,可以认为他们来自的总体均数相等,各处理样本 均数的差异是实验误差造成的
4 参考答案 一、解释以下术语及符号(其中符号解释需要写出名称、公式、含义与作用) 1.样本统计量::指由样本的全部观察值而算得的样本特征数。 2.偶然误差(机误):由于机会不等所造成的偏差。或在试验中由不确定的因数而引起的误 差,具随机性。 3.处理:指事先设计好的实施在试验单位上的一种具体措施或试验中的具体比较项目叫做处 理。 4.重复:每个品种(或处理)占有两个或两个以上的小区称有重复。 5.生物统计学:是数理统计的原理和方法在生物科学研究中的应用,是一门应用数学。 6.小机率原理:概率很小的事件,在一次试验中是不至于发生的。 7.SS:平方和,反应资料的总变异。 8.s y :标准误,估计抽样误差。 9.LSD0.05 :显著水准为 0.05 的最小显著差数的临界值。 10.b:样本的直线回归系数,反映当 x 每变化 1 个单位时 y 的理论变化量。 二、填空题 评分标准:填写正确的数学符号也同样得分 1 系统误差,偶然误差(或随机误差),系统误差,偶然误差(或随机误差)。 2 各个水平,各个简单效应。 3 9,4,9。 4 样本平均数;可信度(或显著水平),上限、下限。 5 单个或两个样本可量(或连续性变数),单个或两个样本计数性(或非连续性变数),适 合性、独立性。 6 LSD 法、SSR 法和 q 法。 三、简答题 2 答: 完全随机设计:试验空间中的各种非试验因素者相当均匀一致的实验条件。一般仅在实 验室试验,温室试验或处理虽多但每处理材料甚少的田间试验中应用。 随机区组设计:适合于有一个方向明显误差的,处理数限于 18 个以内的单、复因子试验, 实施单方面局部控制原则,应用最广泛。 拉丁方设计:适合于有两个明显误差的试验,实施双方面局部控制,处理数限于 5-8 个。 2 答:若 H0:μA=μB=.=μM 成立,根据小概率原理,则接受统计假设 H0,否定 HA , 样本 A、B,.,M 处理的平均数无显著差异,可以认为他们来自的总体均数相等,各处理样本 均数的差异是实验误差造成的

若HO:μA=μg=.=μ,不成立,则拒绝无效统计假设HO,接受H,即样本A、B,.,M 处理间的平均数有显著差异,认为各处理来自的总体均数不全等,需进行处理均数间多重比 较,进一步确定两两处理间的差异。 四、问答题 答:统计假设测验:对两未知集团均数间或者一未知集团与一已知数值(经验数值或标准) 间进行显著性测验。 方差分析法:对多个处理间的差异进行比较。充分利用资料的全部信息提高试验的精确度。 在单因素试验中,可以分辨出最优的水平。在多因素试验中,可以分辨出最优的水平组合。 直线相关与回归:分析两类变量间是否存在直线相关关系以及是否存在回归关系。相关 分析目的:确定两个变量在数量关系上的密切程度和性质。回归分析目的:导出由x来预测 或控制y的回归方程,即确定当自变量x为某一值时依变量y将会在什么范围内变化。 五、计算题 1. 解:统计量(10分):不=9.64 5=1.50s5=22.55 s:=0.45cv=2×10%=15.56 苗高的95%区间估计=X+a.0514×s:=9.64+2.228×0.45=8.63 下限=不-ta.614×S:=10.65 方法1:成对法t测验 统计假设HO:4a=0 3.10 =3.44 s42.85/V10 因|t=3.44>ta.1m=3.25,差异极显著。 结论:处理A的产量极显著高于处理B。 方法2:成组法 统计假设H0:4,=2
5 若 H0:μA=μB=.=μM 不成立,则拒绝无效统计假设 H0,接受 HA ,即样本 A、B,.,M 处理间的平均数有显著差异,认为各处理来自的总体均数不全等,需进行处理均数间多重比 较,进一步确定两两处理间的差异。 四、问答题 答:统计假设测验:对两未知集团均数间或者一未知集团与一已知数值(经验数值或标准) 间进行显著性测验。 方差分析法:对多个处理间的差异进行比较。充分利用资料的全部信息提高试验的精确度。 在单因素试验中,可以分辨出最优的水平。在多因素试验中,可以分辨出最优的水平组合。 直线相关与回归:分析两类变量间是否存在直线相关关系以及是否存在回归关系。相关 分析目的:确定两个变量在数量关系上的密切程度和性质。回归分析目的:导出由 x 来预测 或控制 y 的回归方程,即确定当自变量 x 为某一值时依变量 y 将会在什么范围内变化。 五、计算题 1. 解:统计量(10 分): x = 9.64 s = 1.50 ss = 22.55 s = 0.45 = 100% = 15.56% x s x cv 苗高的 95%区间估计= x + t0.0 5,1 4 sx = 9.64 + 2.228 0.45 = 8.63 下限= x − t0.05,14 sx = 10.65 2、 方法 1:成对法 t 测验 统计假设 H0: d = 0 3.44 2.85 / 10 3.10 = = = sd d t 因|t|=3.44> t0.01(df=9)=3.25,差异极显著。 结论:处理 A 的产量极显著高于处理 B。 方法 2:成组法 统计假设 H0: 1 = 2

+=618+5.21-1.067 5a-=n 10 =-玉=31.2-28.1=2.905df=18 S-到) 1.067 因|t=2.905>ta1a-1s=2.878,差异极显著。 结论:处理A的产量极显著高于处理B。 方法3:方差分析法(过繁,不是最佳方法,略) 3、 变异来源平方和 自由度 方差 F Fo.as 品种 438.54 62.65 25.16* 2.49 3.64 区组 51.92 3 17.31 6.95* 3.07 4.87 误差 52.38 21 2.49 总变异 542.84 31 结论:两品种间差异达极显著,A品种的产量极显著高于B品种。 4、 解: n=9∑x=67∑x2=509∑y=664 ∑y=88∑y2=880 s5,=10.22s5,=19.56 sp=∑w-∑x∑y/n=8.889 ∑xw-∑x∑y/n r=2-远r12产-②㎡1可 或者r= 5p—=0.6287 =0.6287 r=0.62875%,种子重量与苗高相关不显著。 6
6 n s s S x x 2 2 1 ( ) 2 1 2 + − = = 1.067 10 6.18 5.21 = + t= ( ) 1 2 1 2 S x x x x − − = 2.905 1.067 31.2 28.1 = − df=18 因|t|=2.905> t0.01(df=18)=2.878,差异极显著。 结论:处理 A 的产量极显著高于处理 B。 方法 3:方差分析法(过繁,不是最佳方法,略) 3、 变异来源 平方和 自由度 方差 F F0.05 F0.01 品种 区组 误差 438.54 51.92 52.38 7 3 21 62.65 17.31 2.49 25.16** 6.95** 2.49 3.07 3.64 4.87 总变异 542.84 31 结论:两品种间差异达极显著,A 品种的产量极显著高于 B 品种。 4、 解: 9 67 509 2 n = x = x = xy = 664 y 88 880 2 = y = / 8.889 10.22 19.56 = − = = = sp xy x y n ss x ssy 0.6287 [ ( ) / ][ ( ) / ] / 2 2 2 2 = − − − = x x n y y n xy x y n r 或者 = = 0.6287 ssxssy sp r r=0.62875%,种子重量与苗高相关不显著