
生物统计学试题库 六 一、解释以下术语及符号20分 集团: 研究因子: 重复: 保护行: 精确度: 相关性: Sy: x2。: N(2,10): B: 二、填空题20分 1、因试验环境的趋势性变异而导致的误差称为: ,因试验环境的随机 性变异而导致的误差称为:,试验设计的目标是误差, 误差。 2、未对系统误差实行局部控制的试验方法有: ;对单个方向上的系 统误差进行局部控制的试验方法有:;能对两个不同方向上的系统误 差进行局部控制的试验方法有:;研究因子分主次的试验方法 有:
1 生物统计学试题库 六 一、解释以下术语及符号 20 分 集团: 研究因子: 重复: 保护行: 精确度: 相关性: Sy : χ2 c: N(2,10): β: 二、填空题 20 分 1、因试验环境的趋势性变异而导致的误差称为: ,因试验环境的随机 性变异而导致的误差称为: ,试验设计的目标是_ _误差, 误差。 2、未对系统误差实行局部控制的试验方法有: ;对单个方向上的系 统误差进行局部控制的试验方法有: ;能对两个不同方向上的系统误 差进行局部控制的试验方法有: ;研究因子分主次的试验方法 有:

3、点估计是指用 去估计总体平均数;而区间估计是指在规定的 下估计总体平均数的和。 4、 的资料可用t测验法进行显著性分析,而 的 资料则可用卡平方测验法进行显著性分析,测验一未知比例是否与一已知比例 相符作卡平方的 测验,测验2个(或多个)未知比例是否相符作卡平 方的测验。 5、如果A因子有2个水平,B因子有3个水平,采用随机区组试验重复4次, 则方差分析中的总自由度为;区组自由度为;处理组合自由度 为;交互作用的自由度为。 三、简答题10分 1、请说明单因子试验三种方法各自的适用范围。 2、请说明方差分析中F测验与多重比较各自的作用(可举例)。 四、问答题10分 请分别举例说明区间估计、卡平方适合性测验、方差分析、相关回归分析在现 实中的作用。 五、计算题40分 1、对甘蔗含糖量测定得数据:7,8,8,9,9,9,10,10,11,12(单位:%), 计算此资料的平均数、自由度、平方和、标准差、标准误,并求其置信度为95% 的区间。t.0s=2.306;t0.s,g-2.262;t0.5,0=2.228;
2 3、点估计是指用 去估计总体平均数;而区间估计是指在规定的 下估计总体平均数的 和 。 4、 的资料可用 t 测验法进行显著性分析,而_ _的 资料则可用卡平方测验法进行显著性分析,测验一未知比例是否与一已知比例 相符作卡平方的 测验,测验 2 个(或多个)未知比例是否相符作卡平 方的 测验。 5、如果 A 因子有 2 个水平,B 因子有 3 个水平,采用随机区组试验重复 4 次, 则方差分析中的总自由度为 ;区组自由度为 ;处理组合自由度 为 ;交互作用的自由度为 。 三、简答题 10 分 1、请说明单因子试验三种方法各自的适用范围。 2、请说明方差分析中 F 测验与多重比较各自的作用(可举例)。 四、问答题 10 分 请分别举例说明区间估计、卡平方适合性测验、方差分析、相关回归分析在现 实中的作用。 五、计算题 40 分 1、对甘蔗含糖量测定得数据:7, 8, 8, 9, 9, 9, 10, 10, 11, 12 (单位:%), 计算此资料的平均数、自由度、平方和、标准差、标准误,并求其置信度为 95% 的区间。t0.05,8=2.306; t0 .05,9=2.262; t0 .05,10=2.228;
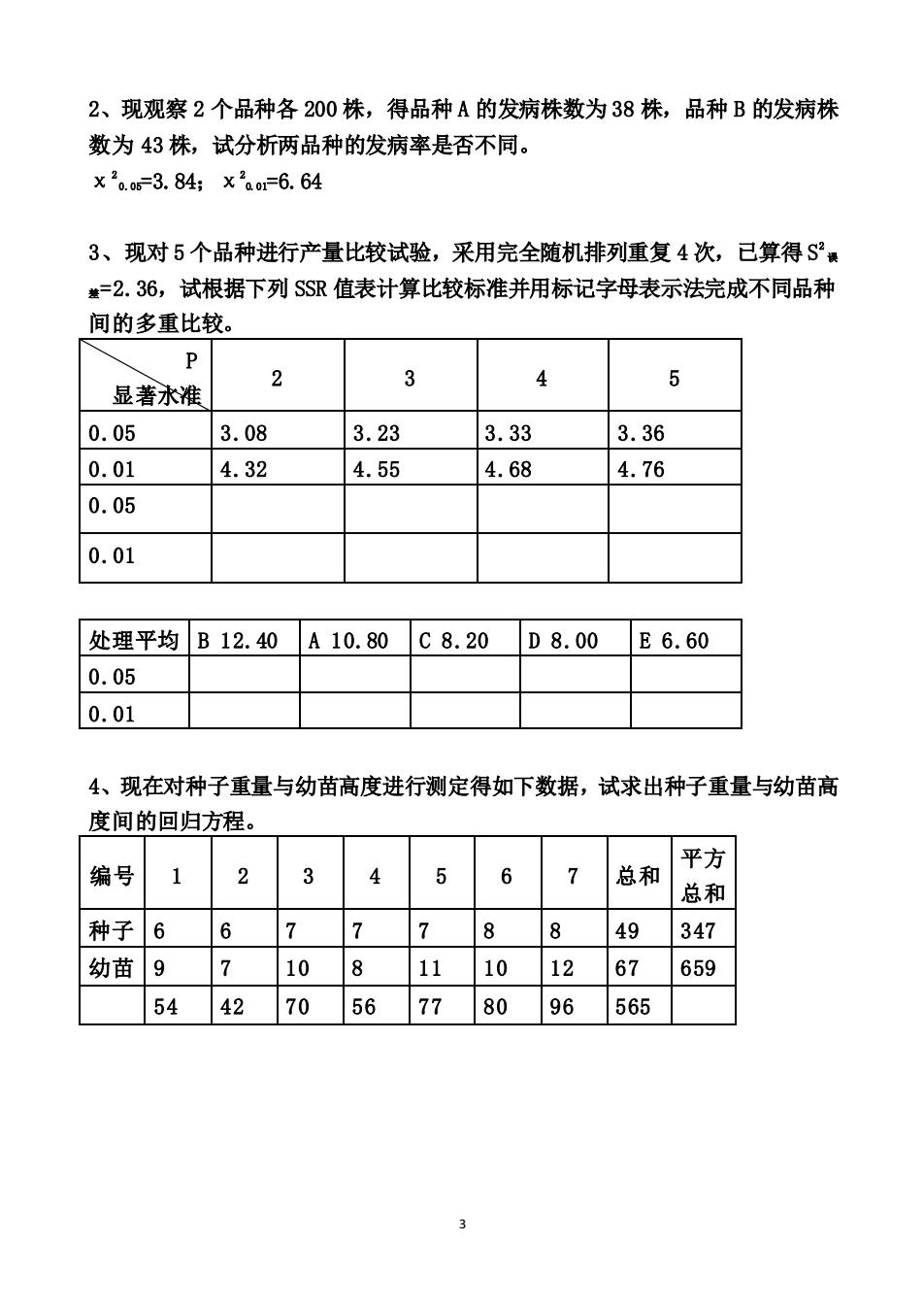
2、现观察2个品种各200株,得品种A的发病株数为38株,品种B的发病株 数为43株,试分析两品种的发病率是否不同。 x20.o6-3.84;x2ao1=6.64 3、现对5个品种进行产量比较试验,采用完全随机排列重复4次,已算得S #=2.36,试根据下列SSR值表计算比较标准并用标记字母表示法完成不同品种 间的多重比较。 2 显著水准 3 4 0.05 3.08 3.23 3.33 3.36 0.01 4.32 4.55 4.68 4.76 0.05 0.01 处理平均B12.40A10.80C8.20 D8.00E6.60 0.05 0.01 4、现在对种子重量与幼苗高度进行测定得如下数据,试求出种子重量与幼苗高 度间的回归方程。 3 平方 编号1 4 6 7 总和 总和 种子66 77 7 8 8 49 347 幼苗9710811101267659 54427056778096565
3 2、现观察 2 个品种各 200 株,得品种 A 的发病株数为 38 株,品种 B 的发病株 数为 43 株,试分析两品种的发病率是否不同。 χ2 0.05=3.84;χ2 0.01=6.64 3、现对 5 个品种进行产量比较试验,采用完全随机排列重复 4 次,已算得 S 2 误 差=2.36,试根据下列 SSR 值表计算比较标准并用标记字母表示法完成不同品种 间的多重比较。 P 显著水准 2 3 4 5 0.05 3.08 3.23 3.33 3.36 0.01 4.32 4.55 4.68 4.76 0.05 0.01 处理平均 B 12.40 A 10.80 C 8.20 D 8.00 E 6.60 0.05 0.01 4、现在对种子重量与幼苗高度进行测定得如下数据,试求出种子重量与幼苗高 度间的回归方程。 编号 1 2 3 4 5 6 7 总和 平方 总和 种子 6 6 7 7 7 8 8 49 347 幼苗 9 7 10 8 11 10 12 67 659 54 42 70 56 77 80 96 565

参考答案 一、解释以下术语及符号 集团:由研究目的确定的、符合指定条件的全部对象 研究因子:对试验指标有影响的,需要被考察的条件 重复:每个处理在试验结束后能获得2个及以上的观测值 保护行:位于试验区域边缘而受边缘效应影响的试验对象,在观测数据时将其 排除在外,则此区域称为保持行 精确度:多次重复观测值之间的符合程度 相关性:当一个变量的值变化时,其他变量的值也随之而变化的趋势 S,:标准误、=S/sqrt()、是样本平均数偏离集团平均数的平均距离, 可反映随机误差的大小 x2:矫正后的卡平方值、=Σ(|a-t|-0.5))/t)、是实际观测值偏离 理论值的平方与理论值之比的和,可以反映实际观测结果与理论情况之间 的差异显著性的大小 N(2,10):均数为2,标准差为10的正态分布 B:集团平均数、反映集团全部个体观测值的一般水平,可作为集团的代 表值 二、填空题 1、因试验环境的趋势性变异而导致的误差称为:系统误差,因试验环境的随 机性变异而导致的误差称为:偶然误差,试验设计的目标是_减小偶然误差, 避免(消除、减小与正确)系统误差
4 参考答案 一、解释以下术语及符号 集团:由研究目的确定的、符合指定条件的全部对象 研究因子:对试验指标有影响的,需要被考察的条件 重复:每个处理在试验结束后能获得 2 个及以上的观测值 保护行:位于试验区域边缘而受边缘效应影响的试验对象,在观测数据时将其 排除在外,则此区域称为保持行 精确度:多次重复观测值之间的符合程度 相关性:当一个变量的值变化时,其他变量的值也随之而变化的趋势 Sy :标准误、=S/sqrt(n)、是样本平均数偏离集团平均数的平均距离, 可反映随机误差的大小 χ 2 c:矫正后的卡平方值、=Σ((|a-t|-0.5)2 )/t)、是实际观测值偏离 理论值的平方与理论值之比的和,可以反映实际观测结果与理论情况之间 的差异显著性的大小 N(2,10):均数为 2,标准差为 10 的正态分布 β:集团平均数、反映集团全部个体观测值的一般水平,可作为集团的代 表值 二、填空题 1、因试验环境的趋势性变异而导致的误差称为: 系统误差 ,因试验环境的随 机性变异而导致的误差称为: 偶然误差 ,试验设计的目标是_减小偶然_误差, 避免(消除、减小与正确)系统 误差

2、未对系统误差实行局部控制的试验方法有:完全随机排列;对单个方向上 的系统误差进行局部控制的试验方法有:随机区组;能对两个不同方向上的 系统误差进行局部控制的试验方法有:拉丁方:研究因子分主次的试验方法 有:裂区设计(条区设计也正确)。 3、点估计是指用样本平均数去估计总体平均数:而区间估计是指在规定的可 靠度下估计总体平均数的下限和上限。 4、服丛正态分布的资料可用t测验法进行显著性分析,而_不服从正太分布_ 的资料则可用卡平方测验法进行显著性分析,测验一未知比例是否与一已知比 例相符作卡平方的适合性测验,测验2个(或多个)未知比例是否相符作卡 平方的独立性测验。 5、如果A因子有2个水平,B因子有3个水平,采用随机区组试验重复4次, 则方差分析中的总自由度为23;区组自由度为3;处理组合自由度为5; 交互作用的自由度为2。 三、简答题10分 1、请说明单因子试验三种方法各自的适用范围。 答:完全随机排列一一试验空间的环境条件不存在趋势性(方向性)变异时: 随机区组一一试验空间的环境条件在1个方向上存在趋势性变异时;拉丁方设 计一一试验空间的环境条件在2个不同方向上存在趋势性变异时。 3、请说明方差分析中F测验与多重比较各自的作用(可举例)。 答:F测验的作用一一测验是否是任意两个处理间的差异均不显著;多重比较的 作用一一测验各处理两两间的差异显著性
5 2、未对系统误差实行局部控制的试验方法有: 完全随机排列 ;对单个方向上 的系统误差进行局部控制的试验方法有: 随机区组 ;能对两个不同方向上的 系统误差进行局部控制的试验方法有: 拉丁方 ;研究因子分主次的试验方法 有: 裂区设计(条区设计也正确) 。 3、点估计是指用 样本平均数 去估计总体平均数;而区间估计是指在规定的 可 靠度 下估计总体平均数的 下限 和 上限 。 4、 服从正态分布 的资料可用 t 测验法进行显著性分析,而_不服从正太分布_ 的资料则可用卡平方测验法进行显著性分析,测验一未知比例是否与一已知比 例相符作卡平方的 适合性 测验,测验 2 个(或多个)未知比例是否相符作卡 平方的 独立性 测验。 5、如果 A 因子有 2 个水平,B 因子有 3 个水平,采用随机区组试验重复 4 次, 则方差分析中的总自由度为 23 ;区组自由度为 3 ;处理组合自由度为 5 ; 交互作用的自由度为 2 。 三、简答题 10 分 1、请说明单因子试验三种方法各自的适用范围。 答:完全随机排列--试验空间的环境条件不存在趋势性(方向性)变异时; 随机区组--试验空间的环境条件在 1 个方向上存在趋势性变异时;拉丁方设 计--试验空间的环境条件在 2 个不同方向上存在趋势性变异时。 3、请说明方差分析中 F 测验与多重比较各自的作用(可举例)。 答:F 测验的作用--测验是否是任意两个处理间的差异均不显著;多重比较的 作用--测验各处理两两间的差异显著性

四、问答题10分 请分别举例说明区间估计、卡平方适合性测验、方差分析、相关回归分析在现 实中的作用。 答: 区间估计的作用:在规定的可靠度(概率)下估计未知集团平均数的取值范围 卡平方适合性测验的作用:测验实验观测到的各类对象间比例是否符合书籍的 理论比例 方差分析的作用:测验多个处理间是否存在显著差异 相关回归分析的作用:当不同变量间存在相关关系时,可用其回归方程进行预 测预报(或优化控制) 举例(略) 五、计算题40分 1、对甘蔗含糖量测定得数据:7,8,8,9,9,9,10,10,11,12(单位:%), 计算此资料的平均数、自由度、平方和、标准差、标准误,并求其置信度为95% 的区间。t.s8=2.306:t0.5,9-2.262:t0.,10=2.228: 7889991010111293 平均数 496464818181100100121144885 96/10=9.3 自由度=10-1=9 平方和=885-93*93/10=20.1 标准差=sqrt(14.4/9)=1.4944 标准误=1.2649/sqrt(10)=0.47 置信区间9.3±2.2620.47[8.24,10.36] 3、现观察2个品种各200株,得品种A的发病株数为38株,品种B的发病株 6
6 四、问答题 10 分 请分别举例说明区间估计、卡平方适合性测验、方差分析、相关回归分析在现 实中的作用。 答: 区间估计的作用:在规定的可靠度(概率)下估计未知集团平均数的取值范围 卡平方适合性测验的作用:测验实验观测到的各类对象间比例是否符合书籍的 理论比例 方差分析的作用:测验多个处理间是否存在显著差异 相关回归分析的作用:当不同变量间存在相关关系时,可用其回归方程进行预 测预报(或优化控制) 举例(略) 五、计算题 40 分 1、对甘蔗含糖量测定得数据:7, 8, 8, 9, 9, 9, 10, 10, 11, 12 (单位:%), 计算此资料的平均数、自由度、平方和、标准差、标准误,并求其置信度为 95% 的区间。t0.05,8=2.306; t0 .05,9=2.262; t0 .05,10=2.228; 平均数 = 96/10=9.3 自由度=10-1=9 平方和=885-93*93/10=20.1 标准差=sqrt(14.4/9)=1.4944 标准误=1.2649/sqrt(10)=0.47 置信区间 9.3±2.262*0.47 [8.24, 10.36] 3、现观察 2 个品种各 200 株,得品种 A 的发病株数为 38 株,品种 B 的发病株 7 8 8 9 9 9 10 10 11 12 93 49 64 64 81 81 81 100 100 121 144 885
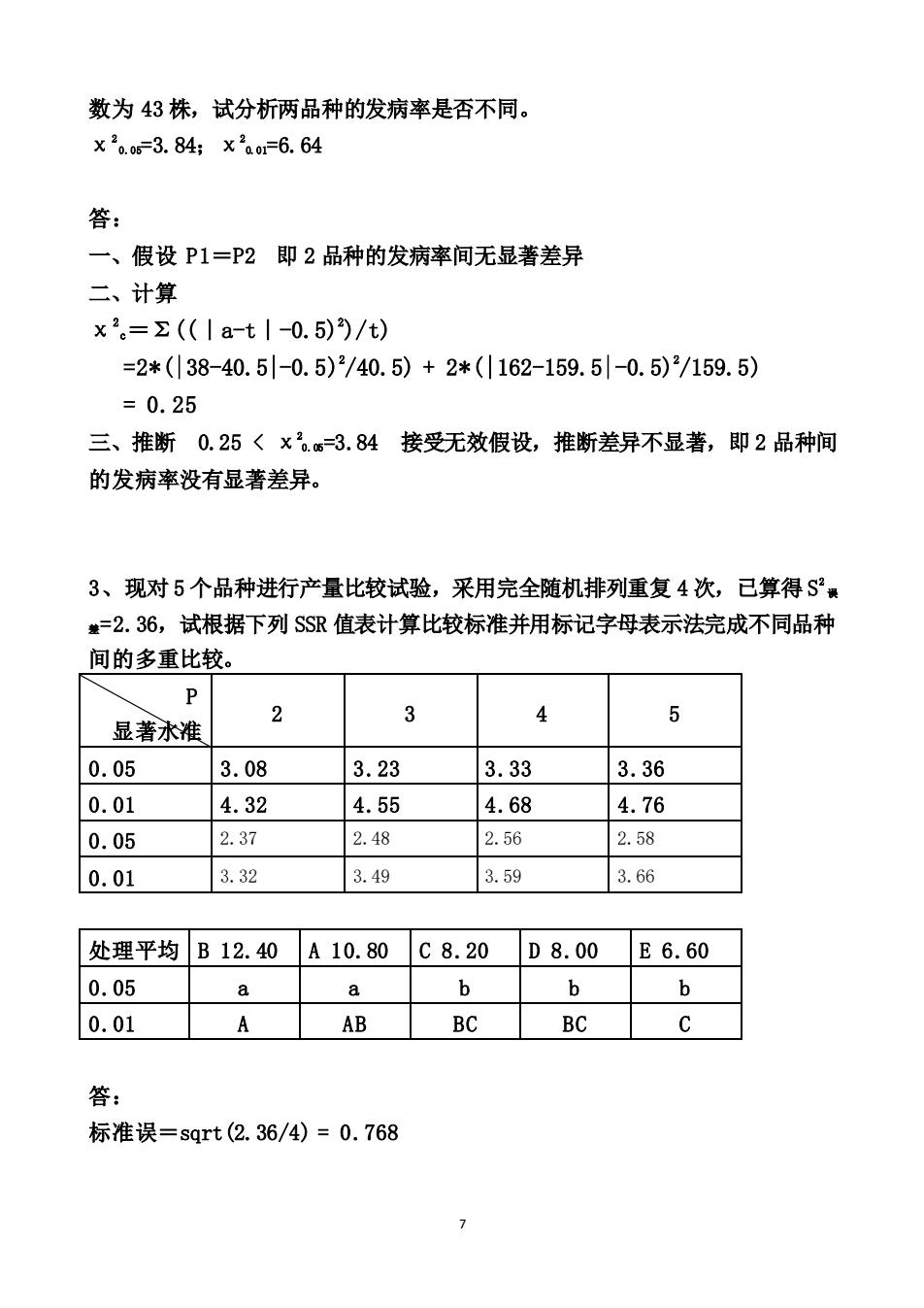
数为43株,试分析两品种的发病率是否不同。 x0.o6-3.84;x2a0r=6.64 答: 一、假设P1=P2即2品种的发病率间无显著差异 二、计算 x2。=Σ(1a-t1-0.5))/t) =2*(38-40.5-0.5)2/40.5)+2*(162-159.5-0.5)2/159.5) =0.25 三、推断0.25〈x。s3.84接受无效假设,推断差异不显著,即2品种间 的发病率没有显著差异。 3、现对5个品种进行产量比较试验,采用完全随机排列重复4次,已算得S =2.36,试根据下列SSR值表计算比较标准并用标记字母表示法完成不同品种 间的多重比较。 4 显著永准 0.05 3.08 3.23 3.33 3.36 0.01 4.32 4.55 4.68 4.76 0.05 2.37 2.48 2.56 2.58 0.01 3.32 3.49 3.59 3.66 处理平均B12.40A10.80C8.20D8.00 E6.60 0.05 a a b 0.01 A AB BC BC 答: 标准误=sqrt(2.36/4)=0.768
7 数为 43 株,试分析两品种的发病率是否不同。 χ2 0.05=3.84;χ2 0.01=6.64 答: 一、假设 P1=P2 即 2 品种的发病率间无显著差异 二、计算 χ 2 c=Σ((|a-t|-0.5)2 )/t) =2*(|38-40.5|-0.5)2 /40.5) + 2*(|162-159.5|-0.5)2 /159.5) = 0.25 三、推断 0.25 < χ2 0.05=3.84 接受无效假设,推断差异不显著,即 2 品种间 的发病率没有显著差异。 3、现对 5 个品种进行产量比较试验,采用完全随机排列重复 4 次,已算得 S 2 误 差=2.36,试根据下列 SSR 值表计算比较标准并用标记字母表示法完成不同品种 间的多重比较。 P 显著水准 2 3 4 5 0.05 3.08 3.23 3.33 3.36 0.01 4.32 4.55 4.68 4.76 0.05 2.37 2.48 2.56 2.58 0.01 3.32 3.49 3.59 3.66 处理平均 B 12.40 A 10.80 C 8.20 D 8.00 E 6.60 0.05 a a b b b 0.01 A AB BC BC C 答: 标准误=sqrt(2.36/4) = 0.768

4、现在对种子重量与幼苗高度进行测定得如下数据,试求出种子重量与幼苗高 度间的回归方程。 平方 编号1 3 4 7 总和 总和 种子6 6 7 7 8 8 49 347 幼苗9 7 108 111012 67 659 5442 7056 7780 96 565 答: 说明:本题的乘积总和为565是错的,正确的是475,故两种计算结果均应给分。 49/7=7 67/7-9.57 SP=475-47*67/7=6.00 SSx=347-49*49/7=4.00 SSy=659-67*67/7=17.71 b=SP/SSx=6/4=1.5 a=9.57-1.5*7=-9.3 回归方程为:y=-9.3+1.5x 当乘积总和用565时的结果为: 49/7=767/7-9.57 SP=565-47*67/7=96.00 SSx=347-49*49/7=4.00 SSy=659-67*67/7=17.71 b=SP/SSx=96/4=24 a=9.57-24*7=-158.43 回归方程为:y=-158.43+24*x
8 4、现在对种子重量与幼苗高度进行测定得如下数据,试求出种子重量与幼苗高 度间的回归方程。 编号 1 2 3 4 5 6 7 总和 平方 总和 种子 6 6 7 7 7 8 8 49 347 幼苗 9 7 10 8 11 10 12 67 659 54 42 70 56 77 80 96 565 答: 说明:本题的乘积总和为 565 是错的,正确的是 475,故两种计算结果均应给分。 49/7=7 67/7=9.57 SP=475-47*67/7 = 6.00 SSx=347-49*49/7 = 4.00 SSy=659-67*67/7 = 17.71 b=SP/SSx = 6/4 = 1.5 a=9.57-1.5*7 = -9.3 回归方程为:y=-9.3+1.5*x 当乘积总和用 565 时的结果为: 49/7=7 67/7=9.57 SP=565-47*67/7 = 96.00 SSx=347-49*49/7 = 4.00 SSy=659-67*67/7 = 17.71 b=SP/SSx = 96/4 = 24 a=9.57-24*7 = -158.43 回归方程为:y=-158.43+24*x