
《数学思想方法》课程教学大纲 课程名称:数学思想方法 课程类别:学科专业必修课 适用专业:小学教育 考核方式:考试 总学时、学分:48学时、3学分 其中实验学时:0学时 一.课程教学目的 通过本课程的学习,使学生了解数学思维方法发展史,能论述数 学发展中的几种重大思维方式:能理解和掌握目前国内比较有代表性 数学思维方法:针对中西数学文化差异、思维模式的角度,梳理了数 学思维方法的作用:对学习者来说能对数学与思维、数学思维方法与 数学教育的发展有比较全面的了解,掌握小学数学教学与教育的具体 方法及要求,认识到数学美学、数学思维方法的发展及研究方向。 二.课程教学要求 1.了解小学数学思维方法的产生与发展。 2.理解和掌握重要的数学思维方法。 3.了解数学思维方法与数学教育的关系。 4.掌握数学思维中的逻辑思维,非逻辑思维和创造性思维的分类、 规律、形式、特征,能在数学学习中的发挥重要作用。 5.能结合化归法不同类型的学习,理解化归法在数学教学和学习 中的地位,并运用化归法解决具体实际问题和具体数学问题,能同时 加以解释数学中的问题。 6.理解逐次渐进方法的意义、分类及应用,掌握逐次渐进应用中 的思维方法。 7.掌握数学解题中常用的方法。例如观察与实验、合情推理、分
《数学思想方法》课程教学大纲 课程名称:数学思想方法 课程类别:学科专业必修课 适用专业:小学教育 考核方式: 考试 总学时、学分: 48 学时 、3 学分 其中实验学时: 0 学时 一.课程教学目的 通过本课程的学习,使学生了解数学思维方法发展史,能论述数 学发展中的几种重大思维方式;能理解和掌握目前国内比较有代表性 数学思维方法;针对中西数学文化差异、思维模式的角度,梳理了数 学思维方法的作用;对学习者来说能对数学与思维、数学思维方法与 数学教育的发展有比较全面的了解,掌握小学数学教学与教育的具体 方法及要求,认识到数学美学、数学思维方法的发展及研究方向。 二.课程教学要求 1.了解小学数学思维方法的产生与发展。 2.理解和掌握重要的数学思维方法。 3.了解数学思维方法与数学教育的关系。 4.掌握数学思维中的逻辑思维,非逻辑思维和创造性思维的分类、 规律、形式、特征,能在数学学习中的发挥重要作用。 5.能结合化归法不同类型的学习,理解化归法在数学教学和学习 中的地位,并运用化归法解决具体实际问题和具体数学问题,能同时 加以解释数学中的问题。 6.理解逐次渐进方法的意义、分类及应用,掌握逐次渐进应用中 的思维方法。 7.掌握数学解题中常用的方法。例如观察与实验、合情推理、分

析与综合、形式化方法与演绎法等,培养运用思维方法解决问题的能 力。 8.理解数学模型在数学教学中的重要性,学会运用数学的思维分 法进行数学建模,培养在数学学习中的建模意识,养成思考的习惯。 9.了解公理化方法的产生、发展、形式及内容,理解公理化方法 与数学教育的关系。 10.了解中西不同的数学教育与不同的数学学习思维,形成正确 的思维方法,为小学数学教育做贡献。 11.了解数学美在数学教育中的作用,正确看待数学学科的真正 的美,来激发学生学习数学的兴趣,从而培养未来数学教师如何进行 数学教育的能力。 三.先修课程 先行课程:空间解析几何初等数论 高等代数 四.课程教学重、难点 教学重点: 1.掌握数学思维中的逻辑思维、非逻辑思维和创造性思维的特征 及在数学教育中的作用。 2.掌握数学教学中常用的数学思维方法 教学难点: 1.理解化归法的不同类型的作用及其应用。 2.理解数学建模的意义及在数学教学中如何引领学生进行数学 建模
析与综合、形式化方法与演绎法等,培养运用思维方法解决问题的能 力。 8.理解数学模型在数学教学中的重要性,学会运用数学的思维分 法进行数学建模,培养在数学学习中的建模意识,养成思考的习惯。 9.了解公理化方法的产生、发展、形式及内容,理解公理化方法 与数学教育的关系。 10.了解中西不同的数学教育与不同的数学学习思维,形成正确 的思维方法,为小学数学教育做贡献。 11.了解数学美在数学教育中的作用,正确看待数学学科的真正 的美,来激发学生学习数学的兴趣,从而培养未来数学教师如何进行 数学教育的能力。 三.先修课程 先行课程 :空间解析几何 初等数论 高等代数 四.课程教学重、难点 教学重点: 1.掌握数学思维中的逻辑思维、非逻辑思维和创造性思维的特征 及在数学教育中的作用。 2.掌握数学教学中常用的数学思维方法 教学难点: 1.理解化归法的不同类型的作用及其应用。 2.理解数学建模的意义及在数学教学中如何引领学生进行数学 建模

五.课程教学方法与教学手段 教学方法:讲授法启发法 自主学习法合作研讨法 教学手段:ppt课件演示 六、课程教学内容 第一章数学思维方法概述(6学时) 1.教学内容 (1)第一节数学思维方法的产生与发展: (2)第二节数学思维方法研究的主要内容: (3)第三节数学史上几种重要的思维方法: (4)第四节数学思维方法与数学教育。 2.重、难点提示 (1)重点:掌握数学思维方法的主要内容和数学史上重要的思维方法。 (2)难点:理解思维、数学思维及数学思维方法的概念,及重要的思维方法。 第二章数学思维中的逻辑思维与非逻辑思维(6学时) 1.教学内容 (1)第一节数学中的逻辑思维: (2)第二节数学中的非逻辑思维: (3)第三节数学中的创造性思维。 2.重、难点提示 (1)重点理解并掌握:数学思维中的逻辑思维和非逻辑思维及创造性思维的意义: (2)难点:培养学生成为未来教师拥有的培养学生的创造性思维的能力。 第三章化归法(8学时) 1.教学内容 (1)第一节化归法概述: (2)第二节变形法: (3)第三节分割法: (4)第四节关系映射反演方法
五.课程教学方法与教学手段 教学方法:讲授法 启发法 自主学习法 合作研讨法 教学手段: ppt 课件演示 六、课程教学内容 第一章 数学思维方法概述(6 学时) 1.教学内容 (1)第一节数学思维方法的产生与发展; (2)第二节数学思维方法研究的主要内容; (3)第三节数学史上几种重要的思维方法; (4)第四节数学思维方法与数学教育。 2.重、难点提示 (1)重点:掌握数学思维方法的主要内容和数学史上重要的思维方法。 (2)难点:理解思维、数学思维及数学思维方法的概念,及重要的思维方法。 第二章 数学思维中的逻辑思维与非逻辑思维 (6 学时) 1.教学内容 (1)第一节数学中的逻辑思维; (2)第二节数学中的非逻辑思维; (3)第三节数学中的创造性思维。 2.重、难点提示 (1)重点理解并掌握:数学思维中的逻辑思维和非逻辑思维及创造性思维的意义; (2)难点:培养学生成为未来教师拥有的培养学生的创造性思维的能力。 第三章 化归法(8 学时) 1.教学内容 (1)第一节化归法概述; (2)第二节变形法; (3)第三节分割法; (4)第四节关系映射反演方法

2.重、难点 (1)重点:理解和掌握化归法中的变形法和分割法在数学学习中的作用: (2)难点:理解化归法的意义。 第四章逐次渐进方法(6学时) 1.教学内容 (1)第一节逐次渐进方法概述: (2)第二节逐次渐进方法的应用: (3)第三节逐次渐进应用中的思维方法。 2.重、难点提示 (1)重点:能利用逐次渐进法的方法解释数学中现象: (2)难点:理解逐次渐进方法内容。 第五章数学解题常用的几种方(8学时) 1.教学内容 (1)第一节数学问题的观察与实验: (2)第二节合情推理与数学解题: (3)第三节分析与综合方法: (4)第四节形式化方法与演绎法。 2.重、难点提示 (1)重点:掌握数学中常见的思维方法在数学教学中作用: (2)难点:理解不同的数学问题如何选择不同的思维方法。 第六章数学模型与数学建模(6学时) 1.教学内容 (1)第一节数学模型与数学建模: (2)第二节数学建模的方法: (3)第三节数学建模与小学教学。 2.重、难点提示 (1)重点:理解和掌握数学模型和数学建模的意义,和数学建模的方法。 (2)难点:理解数学建模在数学学习和教学中的重要性
2.重、难点 (1)重点:理解和掌握化归法中的变形法和分割法在数学学习中的作用; (2)难点:理解化归法的意义。 第四章 逐次渐进方法(6 学时) 1.教学内容 (1)第一节逐次渐进方法概述; (2)第二节逐次渐进方法的应用; (3)第三节逐次渐进应用中的思维方法。 2.重、难点提示 (1)重点:能利用逐次渐进法的方法解释数学中现象; (2)难点:理解逐次渐进方法内容。 第五章 数学解题常用的几种方法(8 学时) 1.教学内容 (1)第一节数学问题的观察与实验; (2)第二节合情推理与数学解题; (3)第三节分析与综合方法; (4)第四节形式化方法与演绎法。 2.重、难点提示 (1)重点:掌握数学中常见的思维方法在数学教学中作用; (2)难点:理解不同的数学问题如何选择不同的思维方法。 第六章 数学模型与数学建模(6 学时) 1.教学内容 (1)第一节数学模型与数学建模; (2)第二节数学建模的方法; (3)第三节数学建模与小学教学。 2.重、难点提示 (1)重点:理解和掌握数学模型和数学建模的意义,和数学建模的方法。 (2)难点:理解数学建模在数学学习和教学中的重要性
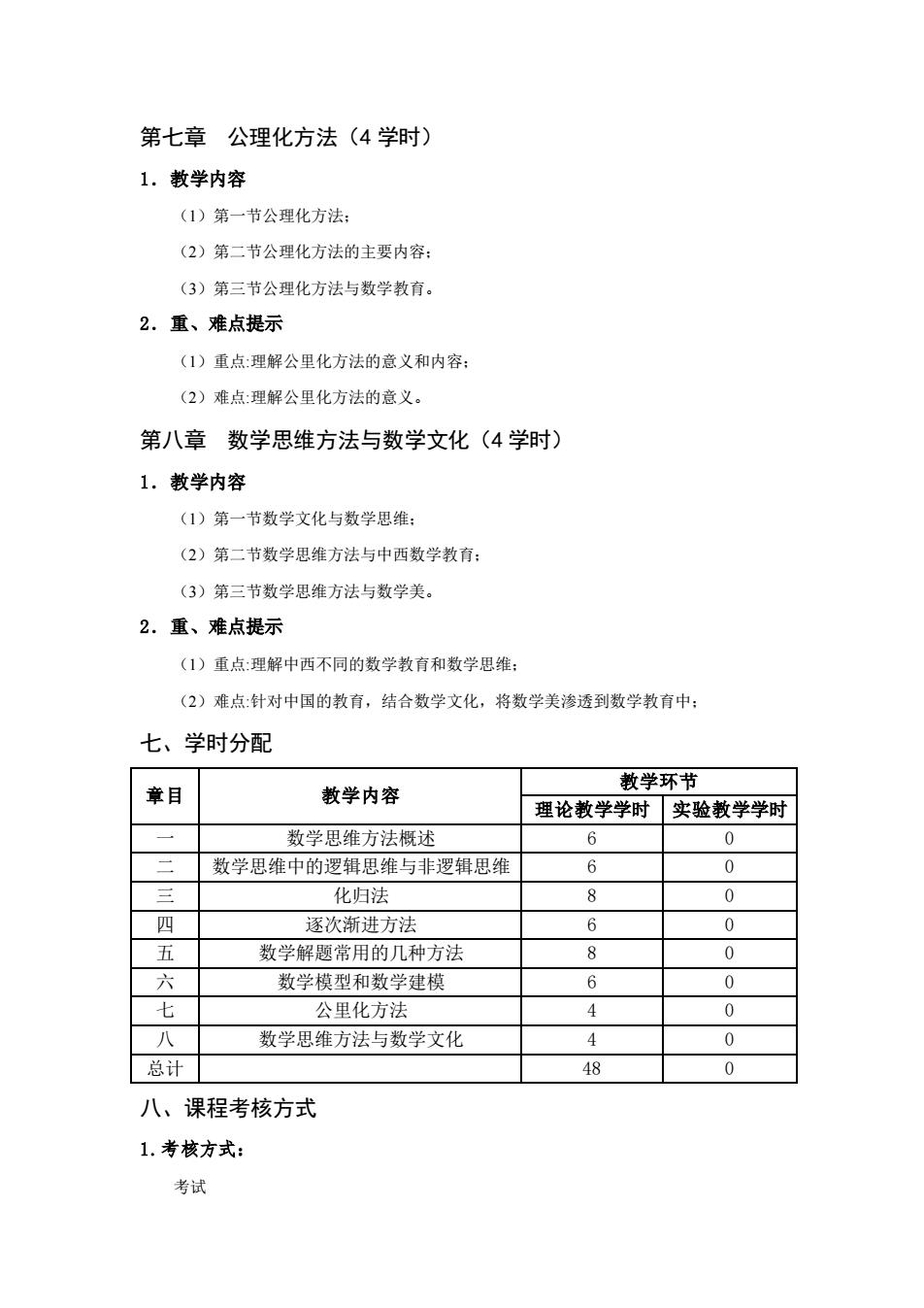
第七章公理化方法(4学时) 1.教学内容 (1)第一节公理化方法: (2)第二节公理化方法的主要内容: (3)第三节公理化方法与数学教育。 2.重、难点提示 (1)重点:理解公里化方法的意义和内容: (2)难点:理解公里化方法的意义。 第八章数学思维方法与数学文化(4学时) 1.教学内容 (1)第一节数学文化与数学思维: (2)第二节数学思维方法与中西数学教育: (3)第三节数学思维方法与数学美。 2.重、难点提示 (1)重点:理解中西不同的数学教育和数学思维: (2)难点:针对中国的教育,结合数学文化,将数学美渗透到数学教育中: 七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 数学思维方法概述 6 0 数学思维中的逻辑思维与非逻辑思维 6 0 三 化归法 8 0 四 逐次渐进方法 6 0 五 数学解题常用的几种方法 8 0 六 数学模型和数学建模 6 0 七 公里化方法 4 0 八 数学思维方法与数学文化 4 0 总计 48 0 八、课程考核方式 1.考核方式: 考试
第七章 公理化方法(4 学时) 1.教学内容 (1)第一节公理化方法; (2)第二节公理化方法的主要内容; (3)第三节公理化方法与数学教育。 2.重、难点提示 (1)重点:理解公里化方法的意义和内容; (2)难点:理解公里化方法的意义。 第八章 数学思维方法与数学文化(4 学时) 1.教学内容 (1)第一节数学文化与数学思维; (2)第二节数学思维方法与中西数学教育; (3)第三节数学思维方法与数学美。 2.重、难点提示 (1)重点:理解中西不同的数学教育和数学思维; (2)难点:针对中国的教育,结合数学文化,将数学美渗透到数学教育中; 七、学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 数学思维方法概述 6 0 二 数学思维中的逻辑思维与非逻辑思维 6 0 三 化归法 8 0 四 逐次渐进方法 6 0 五 数学解题常用的几种方法 8 0 六 数学模型和数学建模 6 0 七 公里化方法 4 0 八 数学思维方法与数学文化 4 0 总计 48 0 八、课程考核方式 1.考核方式: 考试

2.成绩构成 平时作业+期末测试 九、选用教材和参考书目 参考书目: [1]史宁中,《基本概念与运算法则》北京,高等教育出版社,2013年版 [2]史宁中,《义务教育数学课程标准(2011年版)解读》北京师范大学出版 社,2012年版 [3]G.波利亚《数学的发现》北京科学出版社,2006年版 [4]孔凡哲,曾峥《数学学习心理学》北京大学出版社,2012年版 [5]郭思乐《数学思维教育论》上海教育出版社,1998年版 [6]皮亚杰《发生认识论原理》北京商务印书馆,1981年版 [7]任樟辉《数学思维论》南宁,广西教育出版社,1990年版 [8]郑毓信,肖柏荣,熊萍《数学思维与数学方法论》成都,四川教育出版社, 2010年版
2.成绩构成 平时作业+期末测试 九、选用教材和参考书目 参考书目 :