
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破

导航 知识体系构建 实验:探究小车速度随时间变化的规律 /速度公式:v=①yn+t 基本公式{ 位移公式:x=②w+0 位移与速度的关系式:v2-v2=③2心 平均速度:)=④ vo +v 几个推论 位移差:Ax=⑤a卫 匀变速直线运动 v0=0时的比例关系 ⑥倾斜的直线 vt图像(匀变速){加速度等于直线的⑦斜率 运动图像 位移等于图线与时间轴所包围的⑧面积 ⑨倾斜的直线 xt图像(匀速) 速度等于直线的⑩斜率
导航 知识体系构建 实验:探究小车速度随时间变化的规律 匀变速直线运动 基本公式 速度公式:𝒗 = ① 位移公式:𝒙 = ② 位移与速度的关系式:𝒗 𝟐 -𝒗𝟎 𝟐 = ③ 几个推论 平均速度:𝒗 = ④ = 𝒗𝒕 𝟐 位移差:𝚫𝒙 = ⑤ 𝒗𝟎 = 𝟎时的比例关系 运动图像 𝒗𝒕图像(匀变速) ⑥ 的直线 加速度等于直线的⑦ 位移等于图线与时间轴所包围的⑧ 𝒙𝒕图像(匀速) ⑨ 的直线 速度等于直线的⑩ v0+at v0t+𝟏 𝟐 at2 2ax 𝒗𝟎 + 𝒗 𝟐 aT2 倾斜 斜率 面积 倾斜 斜率

导航 特点:只受重力,v0=0,a=①8(竖直向下为正) 速度:v=②@gt 自由落体运动{规律{位移:x=③ 581 速度位移关系式:v2= ④2gX 测重力加速度的方法
导航 自由落体运动 特点:只受重力,𝒗 𝟎 = 𝟎,𝒂 = ⑪ (竖直向下为正) 规律 速度:𝒗 = ⑫ 位移:𝒙 = ⑬ 速度位移关系式:𝒗 𝟐 = ⑭ 测重力加速度的方法 g gt 𝟏𝟐 gt2 2gx

导 专题归纳突破 专题一匀变速直线运动规律解题的常用方法和解题模型 1.匀变速直线运动解题的常用方法和规律特点。 常用 规律特点 方法 般 v-vo+at x=ot+a2-V2=2使用时应注意 y0、y、a、x 公式 是矢量,一般以方向为正方向,其余物理量与正方向相同者 法 为正,与正方向相反者为负
导航 专题归纳突破 专题一匀变速直线运动规律解题的常用方法和解题模型 1.匀变速直线运动解题的常用方法和规律特点。 常用 方法 规律特点 一般 公式 法 v=v0+at x=v0t+𝟏 𝟐 at2 v 2 -𝐯𝟎 𝟐 =2ax 使用时应注意 v0、v、a、x 是矢量,一般以 v0方向为正方向,其余物理量与正方向相同者 为正,与正方向相反者为负

导航 常用方法 规律特点 平均 v- ,对任何性质的运动都适用; 速度法 7=w+,只适用于匀变速直线运动 中间时刻 速度法 V:=7=w+),适用于匀变速直线运动 对于初速度为零的匀加速直线运动或末速度为零的 比例法 匀减速直线运动,可利用比例法求解
导航 常用方法 规律特点 平均 速度法 𝐯 = 𝐱 𝐭 ,对任何性质的运动都适用; 𝐯 = 𝟏 𝟐 (v0+v),只适用于匀变速直线运动 中间时刻 速度法 𝐯𝐭 𝟐 = 𝐯 = 𝟏 𝟐 (v0+v),适用于匀变速直线运动 比例法 对于初速度为零的匀加速直线运动或末速度为零的 匀减速直线运动,可利用比例法求解

导 常用方法 规律特点 把运动过程的“末态”作为“初态”,使运动反向的方 逆向 法。例如,末速度为零的匀减速直线运动可以看作 思维法 反向的初速度为零的匀加速直线运动 应用-图像,可把复杂的物理问题转化为较为简单 图像法 的数学问题解决,尤其是用图像定性分析,可避免繁 杂的计算,快速求解
导航 常用方法 规律特点 逆向 思维法 把运动过程的“末态”作为“初态”,使运动反向的方 法。例如,末速度为零的匀减速直线运动可以看作 反向的初速度为零的匀加速直线运动 图像法 应用v-t图像,可把复杂的物理问题转化为较为简单 的数学问题解决,尤其是用图像定性分析,可避免繁 杂的计算,快速求解
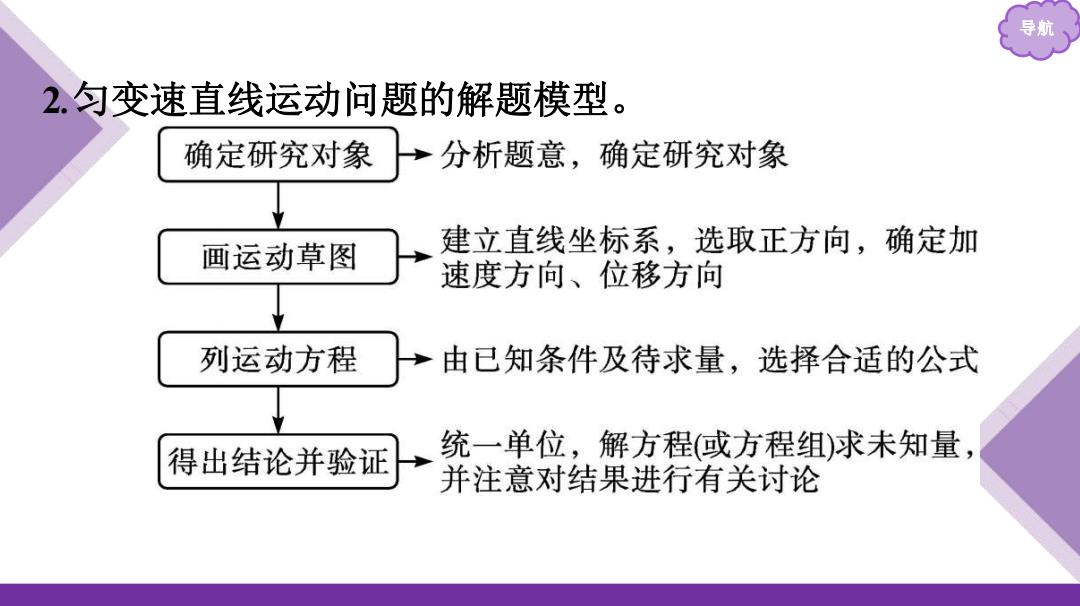
导航 2.匀变速直线运动问题的解题模型。 确定研究对象 →分析题意,确定研究对象 画运动草图 建立直线坐标系,选取正方向,确定加 速度方向、位移方向 列运动方程 由已知条件及待求量,选择合适的公式 得出结论并验证 统一单位,解方程(或方程组)求未知量 并注意对结果进行有关讨论
导航 2.匀变速直线运动问题的解题模型

【典型例题1】在平直的测试汽车加速性能的场地上,每隔 100有一个醒目的标志杆,两名测试员驾车由某个标志杆静 止开始匀加速启动,当汽车通过第二个标志杆开始计时,=10 s时,恰好经过第5个标志杆,,=20s时,恰好经过第10个标志杆, 汽车运动过程中可视为质点,如图所示。 ()求汽车的加速度大小。 23456 (2)若汽车匀加速达到最大速度 64m/s后立即保持该速度匀速 行驶,则汽车从20s末到30s末经过几个标志杆? 答案:(1)2m/s2(2)6个
导航 【典型例题1】在平直的测试汽车加速性能的场地上,每隔 100 m有一个醒目的标志杆,两名测试员驾车由某个标志杆静 止开始匀加速启动,当汽车通过第二个标志杆开始计时,t1 =10 s时,恰好经过第5个标志杆,t2 =20 s时,恰好经过第10个标志杆, 汽车运动过程中可视为质点,如图所示。 (1)求汽车的加速度大小。 (2)若汽车匀加速达到最大速度 64 m/s后立即保持该速度匀速 行驶,则汽车从20 s末到30 s末经过几个标志杆? 答案:(1) 2 m/s2 (2)6个

导 解析:()设汽车的加速度为,经过第二个标志杆的速度为。 在0-10s内有3ewf+号at12 在0~20s内有8=w+2at22 解得=2m/s2。 (2)由(1)解得v=20m/s 第20s时v=y+t2=60m/s 到达最大速度y'=叶△t 代入数据得△2s t3=30s
导航 解析:(1)设汽车的加速度为a,经过第二个标志杆的速度为v0。 在 0~10 s 内有 3l=v0t1+ 𝟏 𝟐 𝒂𝒕 𝟏 𝟐 在 0~20 s 内有 8l=v0t2+ 𝟏 𝟐 𝒂𝒕 𝟐 𝟐 解得a=2 m/s2 。 (2)由(1)解得v0 =20 m/s 第20 s时v=v0+at2 =60 m/s 到达最大速度v'=v+aΔt 代入数据得Δt=2 s t3 =30 s