
第5章化学动力学基础 5.1二甲(CHh0分解为甲烷、氢和一氧化碳的反应的动力学实验数据如下 t/s 0 200 400 600 800 C[(CHh0 mol-dm-30.010000.009160.008390.007680.00703 1)600s和800s间的平均速率. 0.010 0.009 200 X=800时,y=0.00703,800s时的 r=0.00703=878×10-6mol·dn-3:s-1 答:60s和80s间的¥均速率是325x10-m0l·dn3.g (2)800s的瞬间速率为878×10-6mol·dm-3·s 52在970K下,反应2N,O(gN2(g+O(g)起始时N,0的压力为2.9310Pa,并测得反应过 程中系绕的总压变化如下表所示: s 30090020004000 p总)10Pa3.333.633.934.14 求最初300s与最后2000s的时间间隔内的平均速。 解:最初300s内的平均速率 A P -3332.93kPa =13.33Pa·s 300s 最后200s的时间间隔内 =-P-44383=105s 答:最初300内的平均速率是133P·s-,最后200s的时间间隔内平均速率是105P内·s-。 5.3在600K下反应2NO+O,=2NO
第 5 章化学动力学基础 5.1 二甲醚(CH3)2O 分解为甲烷、氢和一氧化碳的反应的动力学实验数据如下: t/s 0 200 400 600 800 C[(CH3)2O]/mol∙ dm-3 0.01000 0.00916 0.00839 0.00768 0.00703 (1)600s 和 800s 间的平均速率。 X=800 时,y=0.00703,800s 时的 r= =8.78×10-6 mol·dm -3·s-1 答: (1)600s 和 800s 间的平均速率是 3.25×10-6 mol·dm -3·s-1 (2)800s 的瞬间速率为 8.78×10-6 mol·dm-3·s-1 5.2 在 970K 下,反应 2N2O(g)=N2(g)+O2(g).起始时 N2O 的压力为 2.93·10 4Pa ,并测得反应过 程中系统的总压变化如下表所示: t/s 300 900 2000 4000 p(总)/10 4Pa 3.33 3.63 3.93 4.14 求最初 300s 与最后 2000s 的时间间隔内的平均速率。 解:最初 300s 内的平均速率 r=- =- =13.33Pa·s-1 最后 200s 的时间间隔内 r=- =- =1.05Pa·s-1 答:最初 300s 内的平均速率是 13.33Pa·s-1,最后 2000s 的时间间隔内平均速率是 1.05 Pa·s-1。 5.3 在 600K 下反应 2NO + O2 = 2NO2 0.00703 800 Δp Δt (3.332.93)kPa 300s Δp Δt (4.14 3.93)kPa 2000s

初始浓度mol-dm-3 初速率mol-dm-3s coNO)co(O2) ro=-dc(NOYdt 0.010 0.010 2.510-3 0.010 0.020 5.010 0.030 0.020 4510-3 (仙)求该反应的表观速率方程 (2)计算速率常数. (3)预计cNO=0.015 mol-dm-3,c02=0.025 mol-dm-3的初速率. 解:(1)油实验数据可见,O2的浓度增加一倍,反应速率就增加一倍:NO的浓度增加3倍,反 应速率就增大为原来的9倍。可见该反应的速率与O,的浓度的一次方呈正比,与NO浓度 的平方呈正比。 故有,=kc2NO(O2) (2)由表中的数据可见,任取一组数据来计算速率常数k,计算结果不会有差别: k=- 0.25×10-3mol.dm3.s i(NO)co(O:) (0.0imol-dmmm5x1mdm (3)6=2.5x103cd(N0)c,(0,) =2.5x103mol2.dm6.s1×(0.015mol.dm3y×0.025 mol.dm3 =0.014mol-dm.s- 答:()该反应的表观速率方程是r ke(NO)o(O2 (2速率常数为2.5×103mo1r2.dm5.g (3)caN0=0.015 mol-dm-3,caO2户0.025 mol-dm-3的初速率时的初速率为0.014mol.dnm.stl 5.4N,0在金表面上分解的实验数据如下: U/min c(N2O)/mol-dm-3 0 0.100 20 0.080 0.060 6 100 0 求分解反应的反应级数 (2)制作该反应的动力学曲线。 (3)求速率常数 (4求N,0消耗一半时的反应速率 (5)该反应的半衰期与初始浓度呈什么关系? 解:()在相等的时间间隔内,N,0浓度的减少量相同,可见反应速率与N0的浓度无关。所以 该反应的反应级数为零
初始浓度/mol∙ dm -3 c0(NO) c0(O2) 初速率/mol∙ dm -3 ∙s-1 r0=-dc(NO)/dt 0.010 0.010 0.010 0.020 0.030 0.020 2.5∙10-3 5.0∙10-3 45∙10-3 (1)求该反应的表观速率方程. (2)计算速率常数. (3)预计 c0(NO)=0.015mol∙ dm -3,c0(O2)=0.025 mol∙ dm -3的初速率. 解:(1)由实验数据可见,O2 的浓度增加一倍,反应速率就增加一倍;NO 的浓度增加 3 倍,反 应速率就增大为原来的 9 倍.可见该反应的速率与 O2的浓度的一次方呈正比,与 NO 浓度 的平方呈正比。 故有,r=kc2(NO)c(O2) (2)由表中的数据可见,任取一组数据来计算速率常数 k,计算结果不会有差别: 3 3 1 3 2 6 1 2 3 3 0 0 2 0.25 10 dm 2.5 10 dm ( ) ( ) (0.01 dm )(0.01 dm ) r mol s k mol s c NO c O mol mol - - ¥ - - × × = = = ¥ × × × × (3) 3 2 0 0 0 2 r = 2.5¥10 c (NO)c (O ) 3 2 6 1 3 2 3 3 1 2.5 10 dm (0.015 dm ) 0.025 dm 0.014 dm mol s mol mol mol s - - - = ¥ × × ¥ × ¥ × = × × 答:(1)该反应的表观速率方程是 r=kc2(NO)c(O2); (2)速率常数为 3 2 6 1 2.5 10 mol dm s - - ¥ × × (3) c0(NO)=0.015mol∙ dm -3,c0(O2)=0.025 mol∙ dm -3 的初速率时的初速率为 3 1 0.014mol dm s - × × 1 5.4 N2O 在金表面上分解的实验数据如下: t/min c(N2O)/mol∙ dm -3 0 20 40 60 80 100 0.100 0.080 0.060 0.040 0.020 0 (l)求分解反应的反应级数。 (2)制作该反应的动力学曲线。 (3)求速率常数。 (4)求 N2O 消耗一半时的反应速率。 (5)该反应的半衰期与初始浓度呈什么关系? 解:(l)在相等的时间间隔内,N2O 浓度的减少量相同,可见反应速率与 N2O 的浓度无关。所以 该反应的反应级数为零
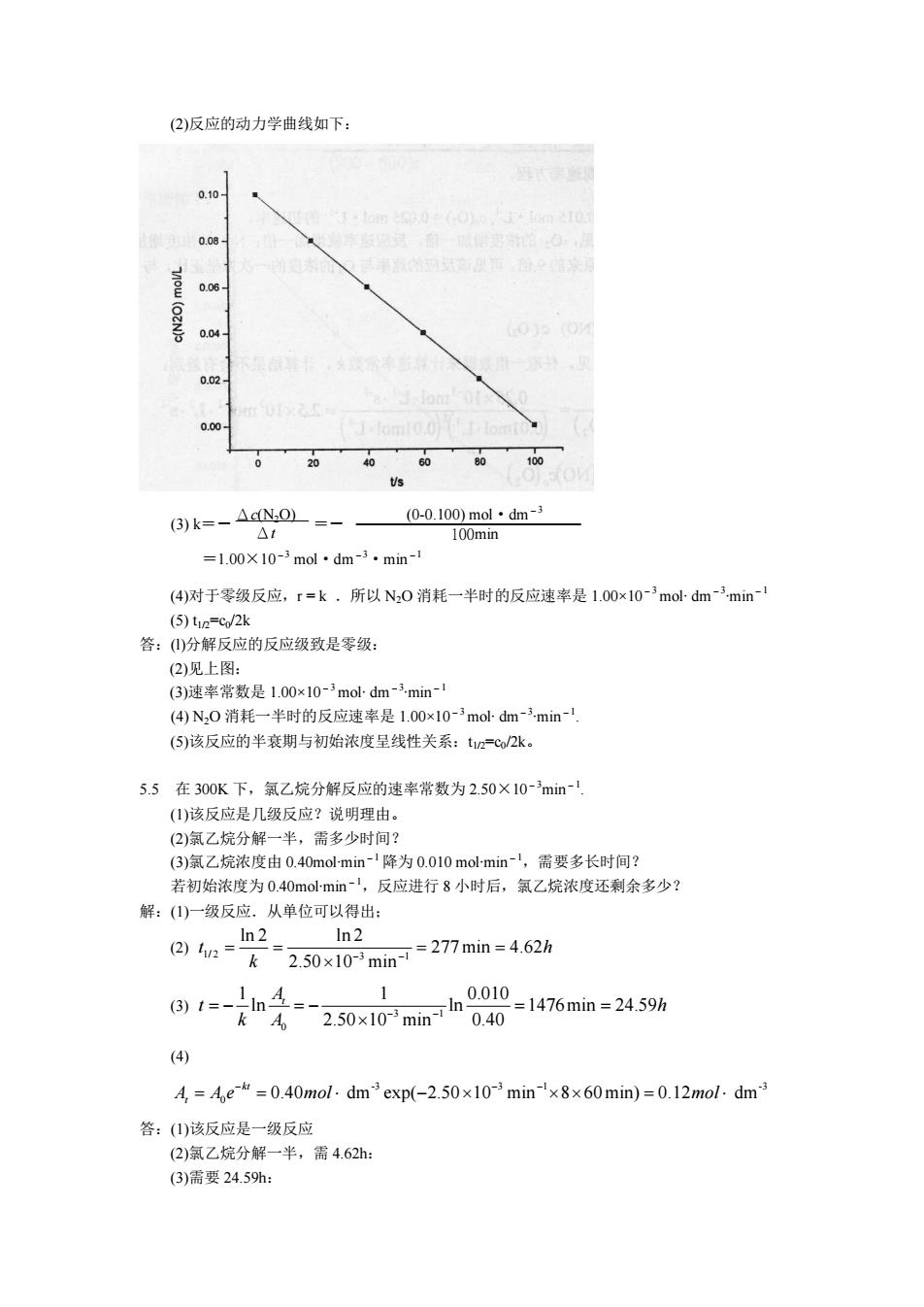
(2)反应的动力学曲线如下: 006 o4 002 0.00 0 (3)k=-△cN.0 0-0.100)mol·dm-3 100mn =1.00X 10-mol dm-3.min-1 (4)对于零级反应,r=k所以N,0消耗一半时的反应速率是1.00x10-mol-dm-min (5)t2c/2k 答:(分解反应的反应级致是零级: (2)见上图: (3)速率常数是100x10-3mo-dm-3min-1 (④N,0消耗一半时的反应速率是100x10-3modm-min (⑤)该反应的半衰期与初始浓度呈线性关系:t1=c/2k。 5.5在300K下,氯乙烷分解反应的速率常数为2.50×10-min- 1该反应是几级反应?说明理由」 (2)氣乙烷分解一半,需多少时间 (3)氯乙烷浓度由0.40m0l-min 降为0.010mol-min,需要多长时间 若初始浓度为0.40 mol-min-1,反应进行8小时后,氯乙烷浓度还剩余多少? 解:()一级反应.从单位可以得出: 2)a=ln2=250x10min=27min=4625 1 8,e_n年=产250x10rmin040=1476mn=2459% A 0.40 (4) =e=0.40mol.dm exp(-2.)=0.12mol.dm 答:(山)该反应是一级反应 (2)氯乙烷分解一半,需4.62h: (3)需要24.59h:
(2)反应的动力学曲线如下: (3) k=- =- =1.00×10-3 mol·dm-3·min-1 (4)对于零级反应,r = k .所以 N2O 消耗一半时的反应速率是 1.00×10-3mol∙ dm-3 ∙min-1 (5) t1/2=c0/2k 答:(l)分解反应的反应级致是零级: (2)见上图: (3)速率常数是 1.00×10-3mol∙ dm-3 ∙min-1 (4) N2O 消耗一半时的反应速率是 1.00×10-3mol∙ dm -3 ∙min-1 . (5)该反应的半衰期与初始浓度呈线性关系:t1/2=c0/2k。 5.5 在 300K 下,氯乙烷分解反应的速率常数为 2.50×10-3min-1 . (1)该反应是几级反应?说明理由。 (2)氯乙烷分解一半,需多少时间? (3)氯乙烷浓度由 0.40mol∙min-1 降为 0.010 mol∙min-1,需要多长时间? 若初始浓度为 0.40mol∙min-1,反应进行 8 小时后,氯乙烷浓度还剩余多少? 解:(1)一级反应.从单位可以得出; (2) 1/ 2 3 1 ln 2 ln 2 277min 4.62 2.50 10 min t h k - - = = = = ¥ (3) 3 1 0 1 1 0.010 ln ln 1476min 24.59 2.50 10 min 0.40 At t h k A - - = - = - = = ¥ (4) 3 3 1 3 0 0.40 dm exp( 2.50 10 min 8 60min) 0.12 dm kt At A e mol mol - - - = = × - ¥ ¥ ¥ = × 答:(1)该反应是一级反应 (2)氯乙烷分解一半,需 4.62h: (3)需要 24.59h: Δc(N2O) Δt (00.100) mol·dm -3 100min

(4氣乙烷浓度还剩余0.12modm-3。 5.6放射性”Co(半衰期t=5.26)发射的强y一辐射广泛用于治疗痛症(放射疗法)。放射性物质 的辐射强度以居里”为单位表示。某医院购买了一个含20居里的钻源,在10年后,辐射强 度还剩余多少? 解:k=n2。n2 25.26a 0.132a A,=A exp(-kt)=20Ciexp(-0.132a-x10a)=5.3Ci 答:在10年后.放射性活度还剩余5.3C1。 5.7碳一14半衰期为5720,今测得北京周口店山顶洞遗址出土的古斑鹿骨化石中的“℃/2℃比 值是当今活者的生物的0.109倍,估算该化石是距今多久?周口店北京猿人距今约50万年.若 有人提议用碳一4法测定它的生活年代,你认为是否可行? 解:=h2。n2 g37200=121x10-a 1 1 答:估算该化石是距今1万8千3百年:用碳一14测定北京猿人距今年代不可行,因年代过于久 远,利余的“℃放射性太弱,会淹没在背景辐射中,测不出来。 5.8实验测得硅烷分解为硅和氢的反应速率常数与温度的关系如下,求该反应的活化能和指前因 子。(1)作图法。(2)线性回归法。 ks-10.0482.349590 TK7738739731073 解:将表中数据处理成下表: (1/TyK-1.29×10-31.15×10-31.03×10-30.93×10-3 Ink -3.340.83 3.89 6.38 可得到nk一T曲线如图所示
(4)氯乙烷浓度还剩余 0.12 mol∙ dm -3。 5.6 放射性 60 27Co (半衰期 t1/2=5.26a)发射的强 γ-辐射广泛用于治疗痛症(放射疗法)。放射性物质 的辐射强度以“居里”为单位表示。某医院购买了一个含 20 居里的钻源,在 10 年后,辐射强 度还剩余多少? 解: 1 1/ 2 ln 2 ln 2 0.132 5.26 k a t a - = = = 1 0 exp( ) 20 exp( 0.132 10 ) 5.3 At A kt Ci a a Ci - = - = - ¥ = 答:在 10 年后.放射性活度还剩余 5.3Ci。 5.7 碳-14 半衰期为 5720a,今测得北京周口店山顶洞遗址出土的古斑鹿骨化石中的 14C/12C 比 值是当今活着的生物的 0.109倍, 估算该化石是距今多久?周口店北京猿人距今约 50 万年. 若 有人提议用碳-14 法测定它的生活年代,你认为是否可行? 解: 4 1 1/ 2 ln 2 ln 2 1.21 10 5720 k a t a - - = = = ¥ 4 4 1 0 1 1 0.0109 ln ln 1.83 10 1.21 10 1 At t a k A a - - = - = - = ¥ ¥ 答:估算该化石是距今 l 万 8 千 3 百年:用碳-14 测定北京猿人距今年代不可行,因年代过于久 远,剩余的 14C 放射性太弱,会淹没在背景辐射中,测不出来。 5.8 实验测得硅烷分解为硅和氢的反应速率常数与温度的关系如下,求该反应的活化能和指前因 子。(1)作图法。(2)线性回归法。 k/s-1 0.048 2.3 49 590 T/K 773 873 973 1073 解:将表中数据处理成下表: (1/T)/K -1 1.29×10-3 1.15×10-3 1.03×10-3 0.93×10-3 lnk -3.34 0.83 3.89 6.38 可得到 lnk-1/T 曲线如图所示:
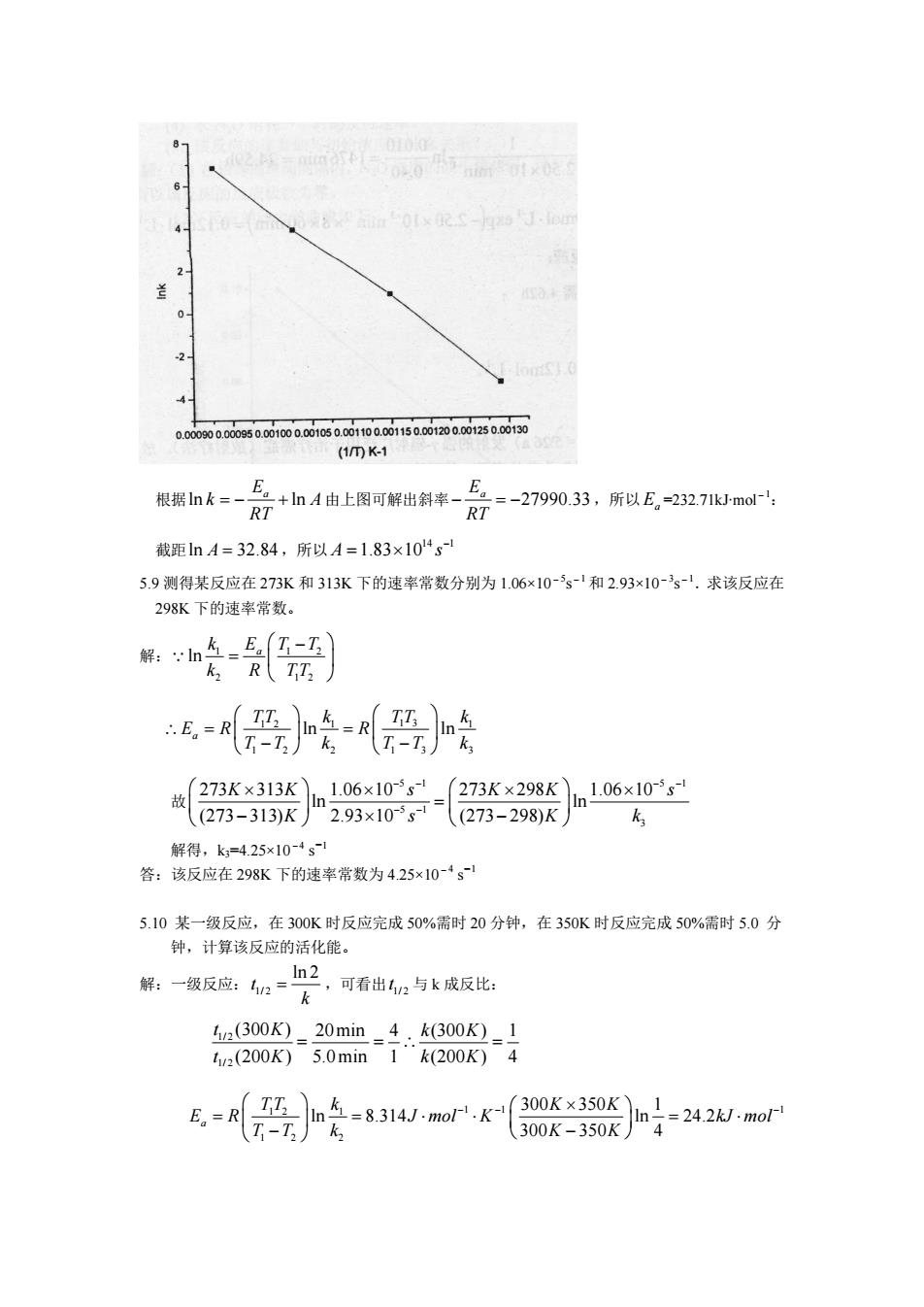
(1mK- 根据nk三-R7+山A由上图可解出斜来-片2三-27990,33,所以E,232,71mo RT 截距nA=32.84,所以A=1.83×104s 5.9测得某反应在273K和313K下的速率常数分别为1.06x10-s-和2.93×10-s-.求该反应在 298K下的速率常数。 解:n车-马(7-工)】 R TT: 恶}经恶 故273K×313Kn106x10s=273K×298Kln106x10-is ((273-313)K 2.93x10s(273-298)K k 解得,k=425x10-1 答:该反应在298K下的速率常数为425×10-·g 5.10某一级反应,在300K时反应完成50%需时20分钟,在350K时反应完成50%需时5.0分 钟,计算该反应的活化能。 解:一级反应:n=h2 ,可看出2与k成反比: (300K)-20min-4.k(300K)_1 12(200K)5.0min1“k200K)4
根据ln ln E a k A RT = - + 由上图可解出斜率 27990.33 E a RT - = - ,所以 Ea =232.71kJ∙mol-1: 截距ln A = 32.84,所以 14 1 A 1.83 10 s - = ¥ 5.9 测得某反应在 273K 和 313K 下的速率常数分别为 1.06×10-5s-1 和 2.93×10-3s-1.求该反应在 298K 下的速率常数。 解: 1 1 2 2 1 2 ln E a k T T k R TT Ê - ˆ = Á ˜ Ë ¯ Q 1 2 1 1 3 1 1 2 2 1 3 3 a ln ln TT k TT k E R R T T k T T k Ê ˆ Ê ˆ \ = = Á ˜ Á ˜ - - Ë ¯ Ë ¯ 故 5 1 5 1 5 1 3 273 313 1.06 10 273 298 1.06 10 ln ln (273 313) 2.93 10 (273 298) K K s K K s K s K k - - - - - - Ê ¥ ˆ ¥ Ê ¥ ˆ ¥ Á ˜ = Á ˜ Ë - ¯ ¥ Ë - ¯ 解得,k3=4.25×10-4 s-1 答:该反应在 298K 下的速率常数为 4.25×10-4 s-1 5.10 某一级反应,在 300K 时反应完成 50%需时 20 分钟,在 350K 时反应完成 50%需时 5.0 分 钟,计算该反应的活化能。 解:一级反应: 1/ 2 ln 2 t k = ,可看出 1/ 2 t 与 k 成反比: 1/ 2 1/ 2 (300 ) 20min 4 (300 ) 1 (200 ) 5.0min 1 (200 ) 4 t K k K t K k K = = \ = 1 2 1 1 1 1 1 2 2 300 350 1 ln 8.314 ln 24.2 300 350 4 a TT k K K E R J mol K kJ mol T T k K K - - - Ê ˆ Ê ¥ ˆ = = × × = × Á ˜ Á ˜ Ë - ¯ Ë - ¯

答:该反应的活化能为24.2 kJ-mol- 5.11若有人告诉你:同一反应,温度越高,温度升高引起反应速率增长的倍数越高。你对此持 肯定意见还是否定意见?在回答上问后,作如下估算:设反应甲、乙两个反应的活化能分 别为:20Jmol和50kJmo1,试对比反应甲、乙温度从300K升高到310K和从500K升 至510K反应速率增长的倍数.并作出归纳如下:速率快的反应与速率小的反应对比,在 相同温度范围内,哪一反应速率增长的倍数高?同一反应,在温度低时和温度高时,温度 升高范围相同时.哪个温度范围反应速率增长的倍数高?试对归纳的结论做出定性的解释。 (此题的假定是:温度改变没有改变反应历程和活化能, 解根器会{ ,代入己知数据,可得 由300K到310K时 单冬=10:2套=191: 由500K到51OK时 =10:冬-127 答:在相同温度范圈内,活化能大的反应速率增长的倍数高,因为k与E成正比:同一反应, 温度升高范围相同时,较低温度范围内反应速紫增大的倍数高,根据山k=一行+n4, k是条对数曲线,自变量越小,曲线越陡,即斜率变化越大,所以T在较低范围内变大时 k增大的倍数越大。 5.12试对比阿仑尼乌斯活化能(表观活化能或实验活化能)、碰撞理论活化能和过渡状态理论活 化能的物理意义,并由此说明表观动力学与分子动力学的不同性。 答:阿仑尼乌斯活化能:阿仑尼鸟斯公式k=A奇中的E,其中B,不随温度改变:碰撞理论 活化能:活化分子的平均能量与反应物分子的平均能量之差:过波态理论活化能:反应物分 子平均能量与处在过渡态的活化络合物分子平均能量之差: 表观动力学中的讨论的是宏观统计平均量:分子动力学是分子水平的平均表现。 5.13表观动力学方程得出的指前因子有没有明确的物理意义?碰撞理论和过渡态理论分别对指 前因子的物理意义是如何理解的?它们的理解是否解释了所有表观动力学方程中指前因了 的物理意义?为什么? 答:表观动力学方程得出的指前因子没有明确的物理意义:碰撞理论的指前因子是频率因子,是 反应系统中单位体积、单位时间内分子之间的碰撞数:过渡态理论的指前因子与过渡态的活 化嫡有关,它实际上是活化分子在全部分子中所占的分数。它们的理解并没有解释了所有表 观动力学方程中指前因子的物理意义。 5.14有人提出氧气氧化溴化氢气体生成水蒸气和溴蒸气的反应历程如下: HBr+O,HOOBr
答:该反应的活化能为 24.2kJ∙mol-1 . 5.11 若有人告诉你:同一反应,温度越高,温度升高引起反应速率增长的倍数越高。你对此持 肯定意见还是否定意见?在回答上问后,作如下估算:设反应甲、乙两个反应的活化能分 别为:20 kJ∙mol-1 和 50 kJ∙mol-1, 试对比反应甲、 乙温度从 300K 升高到 310K 和从 500K 升 至 510K 反应速率增长的倍数.并作出归纳如下:速率快的反应与速率小的反应对比,在 相同温度范围内,哪一反应速率增长的倍数高?同一反应,在温度低时和温度高时,温度 升高范围相同时. 哪个温度范围反应速率增长的倍数高?试对归纳的结论做出定性的解释。 (此题的假定是:温度改变没有改变反应历程和活化能) 解: 根据 1 1 2 2 1 2 ln E a k T T k R TT Ê - ˆ = Á ˜ Ë ¯ ,代入己知数据,可得 由 300K 到 310K 时 甲: 2 1 1.30 k k = ;乙: 2 1 1.91 k k = ; 由 500K 到 51OK 时 甲: 2 1 1.10 k k = ;乙: 2 1 1.27 k k = 答:在相同温度范圈内,活化能大的反应速率增长的倍数高,因为 lnk 与 Ea 成正比:同一反应, 温度升高范围相同时,较低温度范围内反应速率增大的倍数高,根据ln ln E a k A RT = - + , lnk 是条对数曲线,自变量越小,曲线越陡,即斜率变化越大,所以 T 在较低范围内变大时, k 增大的倍数越大。 5.12 试对比阿仑尼乌斯活化能(表观活化能或实验活化能) 、碰撞理论活化能和过渡状态理论活 化能的物理意义,并由此说明表观动力学与分子动力学的不同性。 答:阿仑尼乌斯活化能:阿仑尼乌斯公式 E a RT k = Ae 中的 Ea,其中 Ea 不随温度改变;碰撞理论 活化能:活化分子的平均能量与反应物分子的平均能量之差;过渡态理论活化能:反应物分 子平均能量与处在过渡态的活化络合物分子平均能量之差; 表观动力学中的讨论的是宏观统计平均量;分子动力学是分子水平的平均表现。 5.13 表观动力学方程得出的指前因子有没有明确的物理意义?碰撞理论和过渡态理论分别对指 前因子的物理意义是如何理解的?它们的理解是否解释了所有表观动力学方程中指前因子 的物理意义?为什么? 答:表观动力学方程得出的指前因子没有明确的物理意义;碰撞理论的指前因子是频率因子,是 反应系统中单位体积、单位时间内分子之间的碰撞数;过渡态理论的指前因子与过渡态的活 化熵有关,它实际上是活化分子在全部分子中所占的分数。它们的理解并没有解释了所有表 观动力学方程中指前因子的物理意义。 5.14 有人提出氧气氧化溴化氢气体生成水蒸气和溴蒸气的反应历程如下: HBr + O2→HOOBr

HOOBr+HBr-→2HOBr HOBr+HBr→H,O+Br2 ()怎样由这三个基元反应加和起来得到该反应的计量方程式? (2)写山各基元反应的速率方程 (3)指出该反应有哪些中间体? (4)实验指山,该反应的表观速率方程对于HB和O都是一级的,试指出,在上述历程中, 哪一步基元反应是速控步? (5)推号表观速率方程 解:()HBr+O一HOOB HOOBr+HBr→2HOB +2HOBr+2HBr→2H0+2Br 4HBr+O2→H,O+B3 (2)=k c(HBr)c().=kc(HOOBr)c(HBr):=kc(HOBr)c(HBr) (3)中间体是HOOBr和HBr (4a、若第一步是速控步,则r=kc(HBr)c(O2) b、若第二步是速控步,则r=k,c(HOOBr)C(HBr)…① 根据稳态近似假设则dc(HOOBr)/d≈0 r)-drOBr)) 代入①,得r=kc(HBr)c(O,). c、若第三步是速控步,则r=k,c(HOBr)c(HBr) 同样利用稳态近似假设,可得出表观速率方程为r=kC(HB)c(O,) 5.15有人提出反应2NO(gHC,(g-2NOCI(g)的反应历程如下: NO+ChNOCI NOCL+NO2NOCI 如果第一个基元反应是速控步,该反应的表观速率方程应呈何形式?如果第二个反应是速控 步,该反应的表观速率方程又呈何形式? 解:若第一基元反应是速控步,则r=kc(NO)(Cl,) 若第二基元反应是速控步,则r=kc(NOCL,)C(NO)..② 根据稳态近似假设,d(NOC,)/d≈0 kc(NO)c(Cl,)-kd(NO)c(CL)
HOOBr + HBr→2HOBr HOBr+ HBr→H2O+Br2 (1)怎样由这三个基元反应加和起来得到该反应的计量方程式? (2)写山各基元反应的速率方程。 (3)指出该反应有哪些中间体? (4)实验指山,该反应的表观速率方程对于 HBr 和 O2 都是一级的,试指出,在上述历程中, 哪一步基元反应是速控步? (5)推导表观速率方程。 解: (1) HBr + O2→HOOBr HOOBr+HBr→2HOBr + 2HOBr+2HBr→2H2O+2Br2 4HBr+O2→H2O+Br2 (2) 1 1 2 2 2 3 3 r = k c(HBr)c(O );r = k c(HOOBr)c(HBr);r = k c(HOBr)c(HBr) (3)中间体是 HOOBr 和 HBr (4)a、若第一步是速控步,则 1 2 r = k c(HBr)c(O ) b、若第二步是速控步,则 2 r = k c(HOOBr)c(HBr) ………① 根据稳态近似假设则dc(HOOBr)/ dt ª 0 即 1 2 k c(HBr)c(O )- c(HBr)c(HOOBr) ª 0 \ 1 2 2 ( ) ( ) k c HOOBr c O k = . 代入① ,得 1 2 r = k c(HBr)c(O ) 。 c、若第三步是速控步,则 3 r = k c(HOBr)c(HBr) 同样利用稳态近似假设,可得出表观速率方程为 1 2 r = k c(HBr)c(O ) 5.15 有人提出反应 2NO(g)+Cl2(g)=2NOCl(g)的反应历程如下: NO + Cl2 → NOCl2 NOCl2+ NO → 2NOCl 如果第一个基元反应是速控步, 该反应的表观速率方程应呈何形式?如果第二个反应是速控 步,该反应的表观速率方程又呈何形式? 解: 若第一基元反应是速控步,则 1 2 r = k c(NO)c(Cl ) 若第二基元反应是速控步,则 2 2 r = k c(NOCl )c(NO) .… … ② , 根据稳态近似假设, 2 dc(NOCl )/ dt ª 0 即 1 2 k c(NO)c(Cl ) - 1 2 k c(NO)c(Cl )

:c(NOC,)=上c(C,)代入②得表观速率方程为 r=kc(NO)c(CL) 5.16实验测得反应H(g+2IC(g=2HCI(g)+H(g)对于氢气和氯化碘都是一级的。以下哪一个历 程是具备必要条件的? (a)2ICl(g)+Hz(g)-2HCI(g)+l(g) (b)H(grCI(g)→H(g)+HCl(g(慢) HΠ(g)+ICI(g)→HCI(g)+h2(g(快) (C)H(gHlC(g)一H(g+HC(g(快) Hg+ICIg-→HCg+H (@H(g1CI(g→HCI(g)+H(gX(t慢 Hg)+ICI(g)→HCI(g+I(g(快) HCI(g)→HCI(g+H(g(快) I(g+g→(g快) 解:(a)没有表明决速步是哪一个,所以无法说明H(g+2IC(g=2HC1(g+H,(g对于氢气和氯化 都是 一级”是(a)的必要条件 对于历程b)和d),品gC(g)-H(g+HCI(g(慢)是慢反应,是决速步,而且这个慢反 应是在历程的第一步,而速控步后的任何基元反应对反应速率是丝毫没有贡献的,因此可直 接写出表观速率方程r=kc(H,)c(IC) 对于历程(C,因为H(g1C(g)一HC(gl(g,(慢)是决速步,故有r=k,c(H)C(CI) 根据稳态假设,d四。kcH,c1C-cHmk(1CD0 dt 号cHmc(H,代入r=dHd(IC)得表观速率方程为r=kcH,cIC0岁 ()、(c以、(d)都是具备必要条件的。 5.17温度相同时,三个基元反应的正逆反应的活化能如下: 基元反应 E/kJ-mol-1. E'/kJ-mol-1 55 70 20 16 35 (1)哪个反应的正反应速率最大? 2反应1的反应多大? ()哪个反应的正反应是吸热反应? 解:(1)返应Ⅲ的正反应速率最大因为k=A,E,越小,k越大 (2)△,Hnm=E。-E'=(30-50)kJ-mol-=-25 kJ-mol-1
1 2 2 2 ( ) ( ) k c NOCl c Cl k \ = 代入② 得表观速率方程为 1 2 r = k c(NO)c(Cl ) 5.16 实验测得反应 H2 (g)+2ICl(g)=2HCl(g)+I2 (g) 对于氢气和氯化碘都是一级的。以下哪一个历 程是具备必要条件的? (a) 2ICl(g)+H2 (g)→2HCl(g)+I2 (g) (b) H2 (g)+ICl(g) →HI(g)+HCl(g)(慢) HI(g)+ICl(g) →HCl(g)+I2 (g)(快) (c) H2(g)+ICl(g) →HI(g)+HCl(g)(快) HI(g)+ICl(g) →HCl(g)+I2(g)(慢) (d) H2(g)+ICl(g) →HClI(g)+H(g)(慢) H(g)+ICl(g) →HCl(g)+I(g)(快) HClI(g) →HCl(g)+I(g)(快) I(g)+I(g) →I2(g)(快) 解:(a)没有表明决速步是哪一个,所以无法说明“H2 (g)+2ICl(g)=2HCl(g)+I2 (g)对于氢气和氯化 碘都是一级”是(a)的必要条件: 对于历程(b)和(d ) , H2 (g)+ICl(g) →HI(g)+HCl(g)(慢)是慢反应,是决速步,而且这个慢反 应是在历程的第一步, 而速控步后的任何基元反应对反应速率是丝毫没有贡献的,因此可直 接写出表观速率方程 1 2 r = k c(H )c(ICl) 对于历程(c),因为 HI(g)+ICl(g) →HCl(g)+I2(g),(慢)是决速步,故有 2 r = k c(HI)c(ICl) , 根据稳态假设, d [HI ] dt = 1 2 k c(H )c(ICl ) - 2 k c(HI)c(ICl) ª 0 1 2 2 ( ) ( ) k c HI c H k \ = ,代入 2 r = k c(HI)c(ICl) 得表观速率方程为 1 2 r = k c(H )c(ICl) 答: (b)、(c)、(d)都是具备必要条件的。 5.17 温度相同时.三个基元反应的正逆反应的活化能如下: 基元反应 Ea / kJ∙mol-1 . Ea’/ kJ∙mol-1 . I 30 55 II 70 20 III 16 35 (1)哪个反应的正反应速率最大? (2)反应 I 的反应焓多大? (3)哪个反应的正反应是吸热反应? 解:( 1 )反应 III 的正反应速率最大· 因为 E a RT k = Ae ,Ea 越小,k 越大: ( 2 ) ΔrHm = Ea - Ea’= (30-50) kJ∙mol-1=-25 kJ∙mol-1
(3)反应Ⅱ的正反应是吸热反应.因为△,H5E一E'>0 5.18反应C(s)+C0(g2C0g)的反应格△H=172.5kmol1问:增加总压、升高温度、加入催 化剂,反应的速率常数k、k,反应速率、「,以及平衡常数K将如何变化? 平衡将如何移动?请将你的荆断填入下表: K 平衡移动 方向 增加总压 升高温度 加入催化 k K 平衡移动方向 增加总压 不变 不变 不变 向逆反应方向 升高温度 增大 增大 增大 增大 增大 向正反应方向 加入催化剂 增大增大增大增大不变 平衡不移动 5.19试讨论:对于同一个化学反应.用dn/d,dd,dcd,(dc/仙以及(1/W)dd表达速率 速率方程中速率常数有什么差别? 六贵答洛)器 连*用山a表示.k合不:用d,表示,k含用dc恤表示,k含:用 1 表示,不含以上各项。 520利用表1的数据制作五氧化二氮分解反应的动力学曲线。要求画两条曲线,一条表达五氧 化二氮浓度的变化,另一条表达二氧化氮浓度的变化,并在两条曲线旁标出与表7一1上各 反应时间相应的五氧化二氯和二氧化氮的浓度数值,并对比之。 2.10 、 15×0 0.99×10 0.2 07710 00 1700 0 019 02710-1 解:五氧化二氮分解反应的动力学曲线如下:
( 3 )反应 II 的正反应是吸热反应.因为ΔrHm = Ea - Ea’>0 . 5.18 反应 C( s ) + CO2(g)=2CO(g)的反应焓ΔH=172.5 kJ∙mol-1 问:增加总压、升高温度、加入催 化剂,反应的速率常数 k 正 、k 逆 ,反应速率 r 正 、r 逆 以及平衡常数 K 将如何变化? 平衡将如何移动?请将你的荆断填入下表: k 正 k 逆 r 正 r 逆 K 平衡移动 方向 增加总压 升高温度 加入催化 剂 答: k 正 k 逆 r 正 r 逆 K 平衡移动方向 增加总压 不变 不变 增大 增大 不变 向逆反应方向 升高温度 增大 增大 增大 增大 增大 向正反应方向 加入催化剂 增大 增大 增大 增大 不变 平衡不移动 5.19 试讨论:对于同一个化学反应.用 dn/dt,dζ/dt,dc/dt,(1/V)dc/dt 以及(1/V) dζ/dt 表达速率, 速率方程中速率常数有什么差别? 解: 1 dn 1 d 1 dc V 1 dc d r V dt V dt dt V dt Vdt z z n n n Ê ˆ = = = = = Á ˜ Ë ¯ 速率用 dn/dt 表示,k 含 1 Vn ;用 dζ/dt,表示,k 含 1 V ;用 dc/dt 表示,k 含 1 n ;用(1/V) dζ/dt 表示,不含以上各项。 5.20 利用表 1 的数据制作五氧化二氮分解反应的动力学曲线。要求画两条曲线,一条表达五氧 化二氮浓度的变化,另一条表达二氧化氮浓度的变化,并在两条曲线旁标出与表 7-1 上各 反应时间相应的五氧化二氮和二氧化氮的浓度数值,并对比之。 表 1 解:五氧化二氮分解反应的动力学曲线如下:
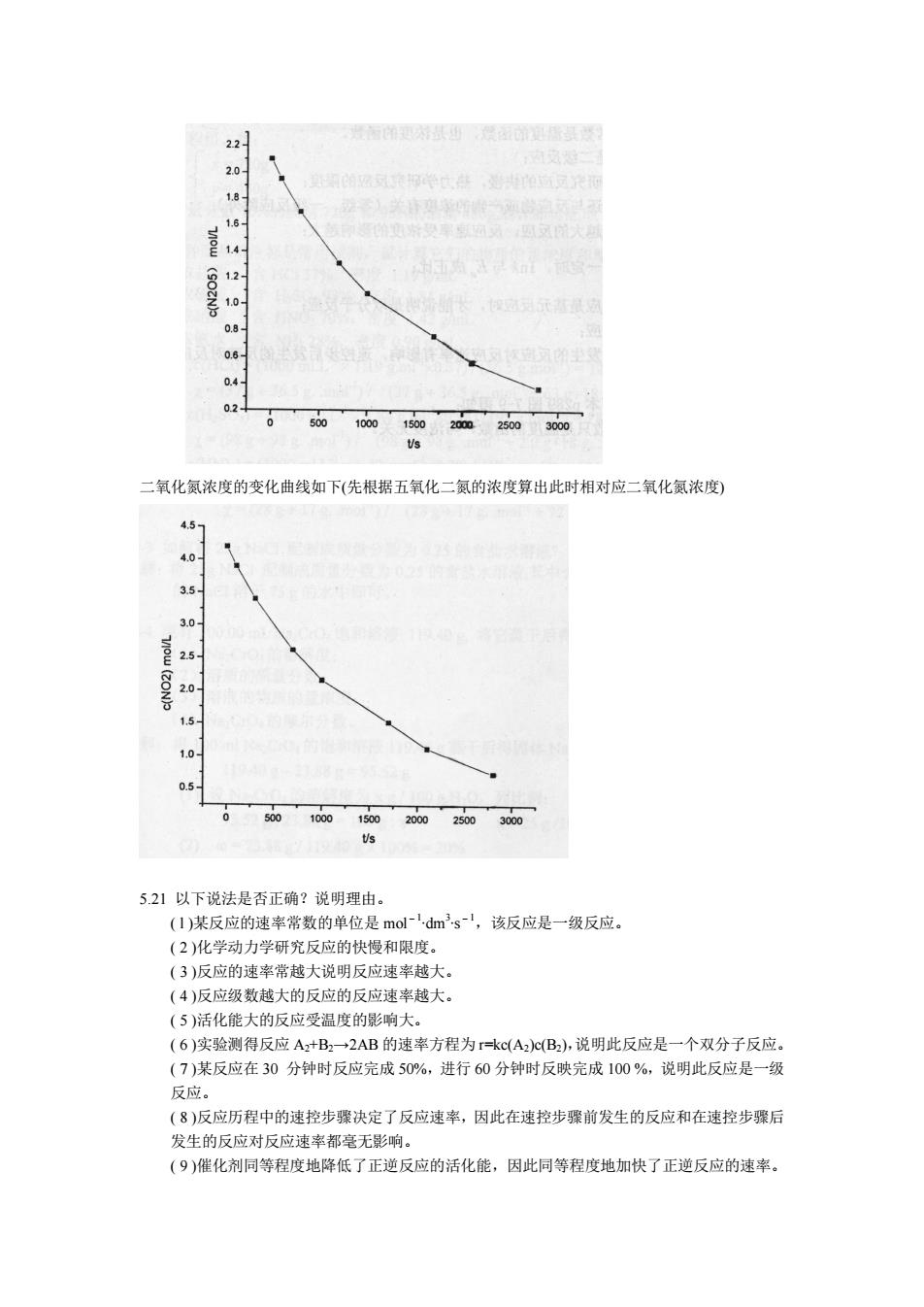
22 1 50100013020m20m300 二氧化氮浓度的变化曲线如下(先根据五氧化二氮的浓度算出此时相对应二氧化氮浓度) 4.5 0 05 521以下说法是否正确?说明理由。 (1)某反应的速率常数的单位是mol-dm3s-',该反应是一级反应。 (2)化学动力学研究反应的快慢和限度。 (3)反应的速率常越大说明反应速率越大。 (4)反应级数越大的反应的反应速率越大 (5)活化能大的反应受温度的影响大。 (6)实验测得反应A+B2一2AB的速率方程为r=kc(AB),说明此反应是一个双分子反应。 (7)某反应在30分钟时反应完成50%,进行60分钟时反映完成100%,说明此反应是一级 反应, (8)反应历程中的速控步骤决定了反应速率,因此在速控步骤前发生的反应和在速控步骤后 发生的反应对反应速率都毫无影响。 (9)催化剂同等程度地降低了正逆反应的活化能,因此同等程度地加快了正逆反应的速率
二氧化氮浓度的变化曲线如下(先根据五氧化二氮的浓度算出此时相对应二氧化氮浓度) 5.21 以下说法是否正确?说明理由。 ( l )某反应的速率常数的单位是 mol-1 ∙dm 3 ∙s-1,该反应是一级反应。 ( 2 )化学动力学研究反应的快慢和限度。 ( 3 )反应的速率常越大说明反应速率越大。 ( 4 )反应级数越大的反应的反应速率越大。 ( 5 )活化能大的反应受温度的影响大。 ( 6 )实验测得反应 A2+B2→2AB 的速率方程为 r=kc(A2)c(B2), 说明此反应是一个双分子反应。 ( 7 )某反应在 30 分钟时反应完成 50%,进行 60 分钟时反映完成 100 %,说明此反应是一级 反应。 ( 8 )反应历程中的速控步骤决定了反应速率,因此在速控步骤前发生的反应和在速控步骤后 发生的反应对反应速率都毫无影响。 ( 9 )催化剂同等程度地降低了正逆反应的活化能,因此同等程度地加快了正逆反应的速率