上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）11、随机变量的数字特征 §4.3 常用随机变量的期望与方差 §4.4 协方差和相关系数 §4.5 矩和协方差矩阵

复习 两个重要的数字特征 X离散型 期望一 随机变量取值的平均水平 8, EX= X离散型 xf(x)c,X连续型 E[8(X)]= g(x)f(x)dc,X连续型 名名，pw (X,Y)离散型 E[g(X,Y)]= g(x,f(x,), (X,Y)连续型 七条性质：·保线性运算·独立性 ·保序性·绝对值性质 柯西一许瓦兹不等式[E(XY)]2≤EX2EY2 +方差 度量随机变量取值在其中心附近的离散程度 YkPk> X离散型 DX=EX-EXP=EY= DX=EX2-(EX)2 f), X连续型 比雪夫不等式P(X-EX≥6)≤DX 四条性质：·D(CX)=C2 ·X与Y独立，则D(X4Y)=DX+DY ·DX≥0；且DX=0÷P(X=C)=1 DX±Y)=DX+DY±2E[(X-EX)(Y-EY)]

复习 两个重要的数字特征                连续型 离散型 y f x dx X y p X DX E X EX EY k k k ( ) , , [ ] 2 1 ——随机变量取值的平均水平             连续型 离散型 x f x dx X x p X EX k k k ( ) , , 期望 1 方差             连续型 离散型 g x f x dx X g x p X E g X k k k ( ) ( ) , ( ) , [ ( )] 1 · 保线性运算 · 独立性 ·保序性 · 绝对值性质 · 柯西—许瓦兹不等式 [E(XY)]2  EX 2 EY 2 七条性质: ——度量随机变量取值在其中心附近的离散程度 DX = EX 2 -(EX ) 2 2 (| | )   DX 切比雪夫不等式 P XEX   · D(CX )=C2 DX ·X 与Y 独立,则D(X+Y )= DX+DY · DX ≥0; 且 DX= 0  P(X=C)=1 D(X±Y )= DX + DY ± 2 E [(X- EX )(Y- EY )] 四条性质：                   连续型 离散型 ( , ) ( , ) , ( , ) ) , ( , ) , ( [ ( , )] 1 1 g x y f x y dxdy X Y g x y p X Y E g X Y i j ij i j

§4.3 常用随机变量的期望与方差 分布 分布列或分布密度 期望 方差 (0-1) P(X=k)=pkql-k k=0,1,00,k=0,1, 2 U(a,b) f(x)= b-a, M≤x≤b; 互相 a+b (b-a)2 0, 其它 确定 2 和参数关联 12 E(2) 2ex≥0 f(x)= 九>0 0, x0 体现了随机变量数字特征的重要性

分布 分布列或分布密度 期望 方差 B(n, p) (0—1) U(a, b) E() p pq np npq         0, 其它 ; , 1 ( ) a x b b a f x , 0 ) 2 ( ) exp( 2 1 ( ) 2 2                x f x P(Xk) pk q1k k n k n P(Xk)Ck p q  P( ) 0 0 , 0 , 0 ( )            x e x f x x   2 ab 12 ( ) 2 ba N(,  2 2) ! ( ) k e P X k k       1 2 1  体现了随机变量数字特征的重要性 §4.3 常用随机变量的期望与方差 可 以 互 相 确 定 均 和 参 数 关 联 k0,1, 0 p1, pq1 k0,1,  ,n, 0 p1, pq1  0, k 0,1, 

二项分布X~B(n,p),P(X=k)=C张pq”-k,k=0,L,,n,0<p<1,p+q=1 X表示n重贝努里试验中的“成功”次数 两种方法：①用定义或简化公式： ②用性质 若设x 第次试验成功 i=1,2,…,n 第次试验失败 则X=之X;是n次试验中成功的次数， i=1 且P(X=1)=p,P(X=0)=1-p,:EX,=1p+0(1-p)=p,EX2=p, 故DX=EX2-(EX)2=p-p2=p(1-p)=p4,il,2,…,n 由于X,,X,相互独立，EX=EX,=pDX=名DX=m4 i-1 0-1分布—EX=p;DX=Pq

X 表示n 重贝努里试验中的“成功” 次数 若设     第 次试验失败 第 次试验成功 i i Xi 0 1 i=1,2,…,n 故 DXi = EXi 2 -(EXi) 2 ∵ EXi =1·p + 0·(1-p )= p, EXi 2 = p, 则  是n次试验中成功的次数，   n i X Xi 1 = p – p 2 = p (1 -p) = p q， i=1, 2,„, n 二项分布 由于X1, „, Xn相互独立，    n i DX DXi 1 = npq. 且 P(Xi=1)= p, P(Xi=0)=1-p, 两种方法： ① 用定义或简化公式； ② 用性质 0-1分布—— EX  p; DX  pq.  = np;    n i EX EXi 1 , ( ) k n k n P Xk Ck p q  X~B k0,1,  ,n, 0 p1, pq1 (n, p)

第二种方法：P(X=K)=Cpq-k k=0,1,2,…n, p+q=1 EX=宫Cpgt=p2Cpqs kC的=nC k=1 是p∑C1p”q-"=p(p+g)-1=m; X=言kCpg=p2Cp-g 起p∑(m+1)Cm1p”q”-m n=0 mmpgC2 =np(n-1)+1]=np(np+q), .DX=np(np+q)-(np)2=npq

k k n k P X k Cn p q  (  )     n k k k n k EX kCn p q 0        n k k k n k np Cn p q 1 1 1 1          1 0 1 1 1 n m m m n m n m k np C p q  np； k  0,1,2, n, p  q  1 1 ( )    n np p q 1 1    k n k kCn nC 第二种方法：                     1 0 1 1 1 0 1 1 n m m m n m n n m m m n m np mCn p q C p q 2 DX  np(np q)(np)    n k k k n k EX k Cn p q 1 2 2       n k k k n k np kCn p q 1 1 1 1           1 0 1 1 1 ( 1) n m m m n m n m k np m C p q  np (n-1) + 1   np(np q), = npq

Poisson分布P(X-k)-若e, k=0,1,2,… Er-24若e (K)-名eA k=0 =ey21 台(k-) 含贫 =知容4 兰 e2m 型e含m+山品 mom! m=0 =λe-ei g+名 =九 =e(2e+e) =几（元+1）， ∴.DX=(2+1)-2=元

, ! ( )     e k P X k k       e k EX k k k 0 !        1 1 k ( 1)! k k e           0 1 m ! m m k m e    k  0,1,2,      k 0 ! k k e        e k E X k k k 0 2 2 ! ( )        1 1 k ( 1)! k k e k            0 1 ! ( 1) m m m k m e m                     1 0 1 ( 1)! m ! m m m m m e      ( )     e e  e   ( 1)， 2  DX  ( 1)   ,   e e   Poisson 分布 = 

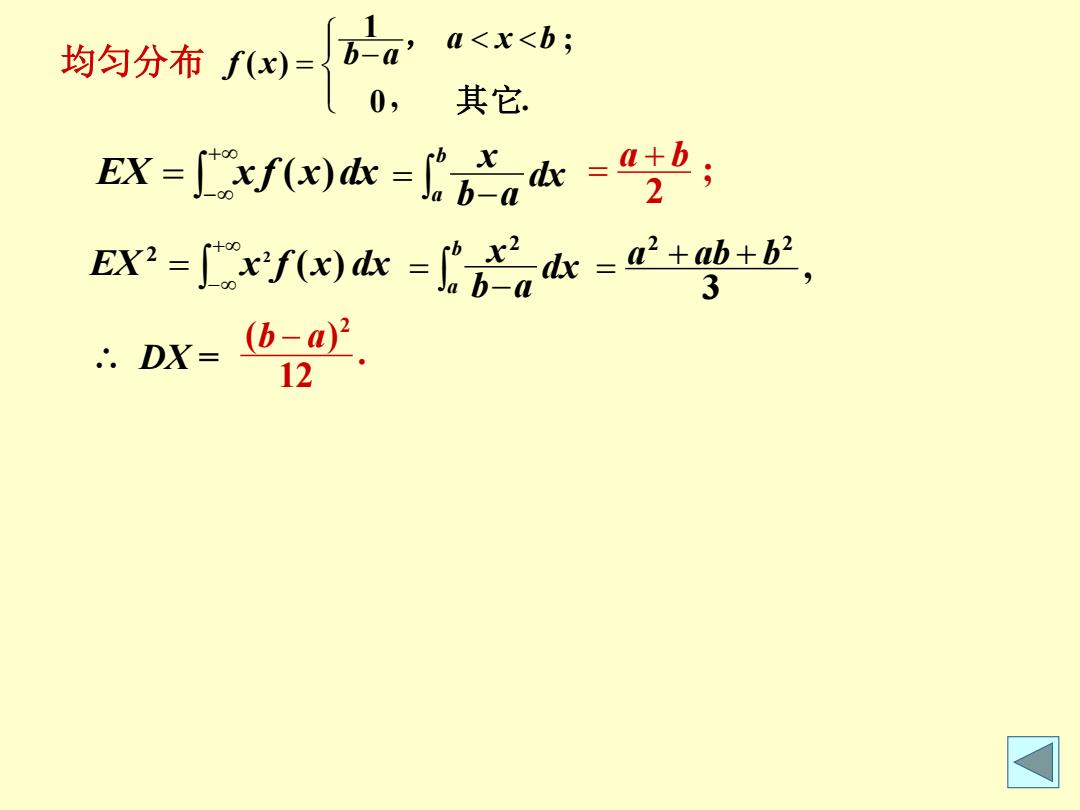
均的分布四 axxchi 其它 BX=fw=6ac-生 xX2=∫e/)==a++E, 3 :DX=(b-a. 12 ☑

        0 , . ; 1 ( ) 其 它 ， a x b b a f x dx b a b x a   ; 2 a  b  dx b a b x a   2 , 3 2 2 a  ab  b  . 12 ( ) 2 b  a EX x f x dx     ( ) EX x f x dx     ( ) 2 2 均匀分布 ∴ DX =

指数分布= EX=0xes是tet=2=元 "x"e *dx =I(r)(r>0) T(r+1)=r(r) r(1)=n: r为整数n时，T(n+1)=n! EX)=2e兰京eh是-是， Dx=是-党=亮. ✉

       0. 0 , , 0; ( ) x e x f x x  EX x e dx x     0   t e dt x t t      0 1     (2)  ； 1  E X x e dx x     0 2 2 ( )   t e dt x t t      0 2 2 1   2 (3)    , 2 2   2 2 ) 1 ( 2   DX   指数分布 . 1 2   ( ) ( 0) 0 1        x e dx r r r x   (r 1)  r(r) r 为整数 n 时， (n+1) = n! (1)= n!

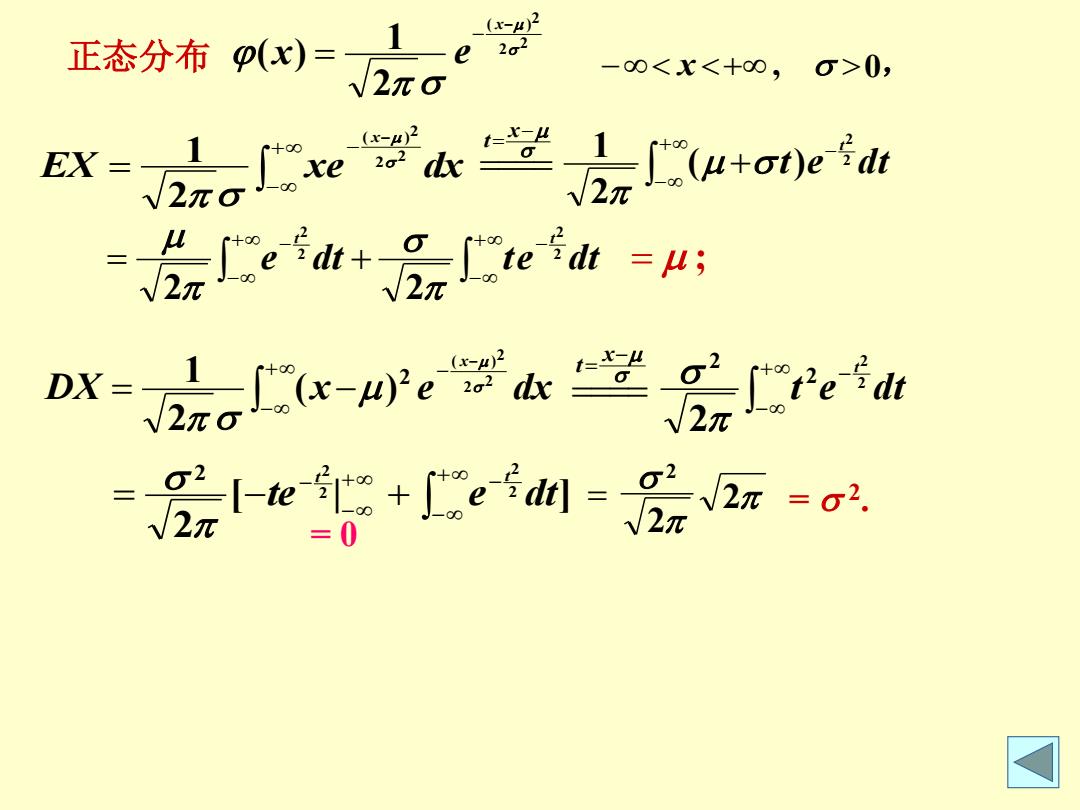
正态分布p(x)= 2o2 -00 (x-) e+e=A oN2aa,学.m 2元e+e训-azr-o2 0 ☑

2 2 2 ( ) 2 1 ( )         x x e EX xe dx x       2 2 2 ( ) 2 1     t e dt t x t         2 2 ( ) 2 1      e dt te dt t t           2 2 2 2 2 2      ; 正态分布  x  ,  0， DX x e dx x        2 2 2 ( ) 2 ( ) 2 1      t e dt t x t        2 2 2 2 2    [ | ] 2 2 2 2 2 2 te e dt t t                2 2 2  = 2 . = 0

另外，几何分布X~G(p) EX=DX=D1 超几何分布X~H(n,M,N) E=4, N' DX=IM(N-M)(N-n) N2(N-1) 更多的可查P132附表1. 例1(P.165例20)设(X,Y)~N(a,b,o1,o,p),求E(2X-3Y+1). 解由条件知X~N(a,o),Y~N(b,o),.EX=M,EY=b, ∴.E(2X-3Y+1)=E(2X)-E(3)+E(1)=2a-3b+1

几何分布 X ~ G( p) ; p2 q , DX  1 p EX  超几何分布 X ~ H(n, M, N) . ( 1) ( ) ( ) 2     N N nM N M N n ， DX N EX  nM 另外， 更多的可查 P132 附表1. 例1(P.165 例20)设 ( , ) ~ ( , , , , ), 2 2 2 X Y N a b 1   求 E(2X-3Y+1). 解 由条件知 ~ ( , ), ~ ( , ), 2 2 2 X N a 1 Y N b  ∴ EX = a , EY = b, ∴ E(2X-3Y+1)= E(2X)-E(3Y)+ E( 1) = 2a - 3b + 1

例2设X,X2,X3相互独立，且X1~U[0,6],X2~P(3), X3~N(0,22),记Y=X1-2X2+3X3,求DY. 解由条件知DX1=62/12=3,DX2=3, DX=22=4, DY=D(X1-2X2+3X3)=DX1+4DX+9DX=46. 例3设X~E(2),求P(X>VDX). 解由条件知X的分布函数为 PCx) xDr)=1-P(X≤VDX)=1-P(X≤分)=1-F分) =1-(1-e-)=e-1

且 X1 ~ U[0, 6], X2 ~ P(3), X3 ~N(0, 2 2), 例2 设 X1, X2, X3 相互独立， 记 Y = X1 - 2X2 + 3X3 , 求 DY . 解 由条件知 DX1 = 62 /12 = 3 , DX3 = 22 DX2 = 3 , = 4 , DY =D(X1 - 2X2 + 3X3 ) = DX1 + 4DX2 + 9DX3 = 46 . 例3 设 X ~ E(), 求 P(X  DX ) . 解 由条件知 X 的分布函数为         0 , 0 , 1 , 0; ( ) x e x F x  x 且 X 的方差为 , 1 2  DX  P(X  DX ) 1 P(X  DX ) ) 1 1 (    P X  ) 1 1 (    F  1（1e 1） . 1  e