
复习 抽样定理 两类 参数估计 已知含有未知参数B总体的分布函数为 F(x;O),利用总体的抽样样本X,X2,·,Xm对参数0或O的 某已知函数g(0)作出估计. 区间估计一一 设法得到参数空间®的一个取值范围,使待估 参数以较大的概率含于其内. 点估计一一 构造适当的统计量X,X2,…Xm)得到0的估计值 矩估计法 一一用样本矩估计总体矩 极大似然法 Ex=8(8,,8)=语9 E(X)=82(0,,)=1主X, E(X)=8,(8,…,0)=h2X
复习 抽样定理 参数估计 —— 两类 利用总体的抽样样本 X1, X2,„, Xn 对参数 或 的 某已知函数 g( )作出估计. ——已知含有未知参数 总体的分布函数为 F(x ; ), 区间估计 点估计 ——构造适当的统计量(X1, X2,„Xn )得到 的估计值 —— 设法得到参数空间 的一个取值范围, 使待估 参数以较大的概率含于其内. 矩估计法 极大似然法 ——用 样本矩 估计 总体矩 先求出总体k 阶原点矩E(Xk) ( ) ( , , ) ( ) ( , , ) ( , , ) 1 2 1 2 1 1 l l l l l E X g E X g EX g , 1 , 1 , 1 1 1 2 1 n i l i n i i n i i X n X n X 极大似然法 n

二、极大似然法 在总体分布类型已知条件下使用的一种参数 估计方法.它首先由德国数学家高斯在1821年提出的. 然而,这个方法常归功于英国统计学家费歇.他在 1922年重新发现了这一方法,并首先研究了这种方法 的一些性质 极大似然法的基本思想 先看一个简单例子:某位同学与一位猎人一 起外出打猎.一只野兔从前方窜过.只听一声枪 响,野兔应声倒下, 如果让你推测是谁打中的,你会如何想呢? 一般会想:只一枪就打中了,而猎人命中的概率一般 大于这位同学命中的概率.这一枪应是猎人射中的. 此例所作的推断已经体现了极大似然法的基本思想 再看一个例子,以进一步体会极大似然法的基本思想
只听一声枪 响, 野兔应声倒下. 某位同学与一位猎人一 起外出打猎. 他在 1922年重新发现了这一方法, 并首先研究了这种方法 的一些性质 . 极大似然法的基本思想 —— 在总体分布类型已知条件下使用的一种参数 估计方法 . 它首先由德国数学家高斯在1821年提出的. Fisher 然而, 这个方法常归功于英国统计学家费歇. 二、极大似然法 先看一个简单例子: 一只野兔从前方窜过. 如果让你推测是谁打中的, 你会如何想呢 ? 而猎人命中的概率一般 大于这位同学命中的概率. 这一枪应是猎人射中的. 再看一个例子, 以进一步体会极大似然法的基本思想. 此例所作的推断已经体现了极大似然法的基本思想. 一般会想: 只一枪就打中了
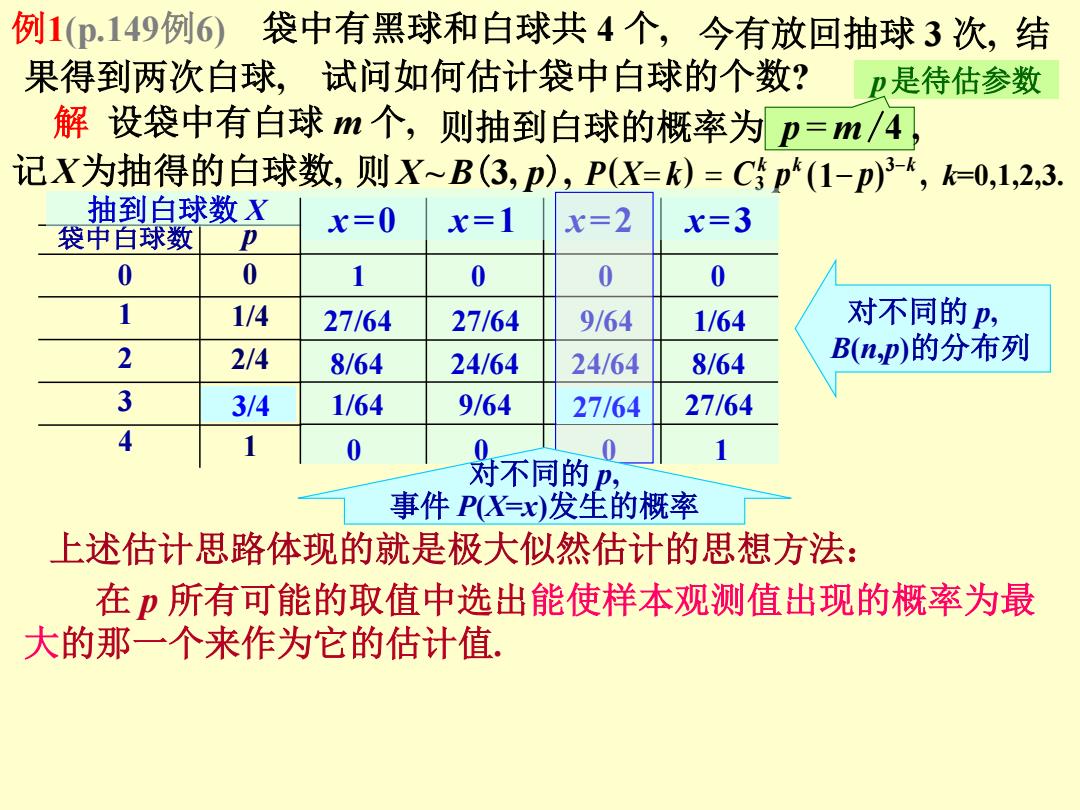
例1(p.149例6)袋中有黑球和白球共4个,今有放回抽球3次,结 果得到两次白球,试问如何估计袋中白球的个数? P是待估参数 解设袋中有白球m个,则抽到白球的概率为p=m/4 记X为抽得的白球数,则X~B(3p),PX=k)=Cp“(1-p)3,k=0,1,2,3. 抽到白球数X x=0 袋中白球数 x=1 x=2 x=3 0 0 1 0 0 0 1 1/4 27/64 27/64 9164 1/64 对不同的P, 2 2/4 8/64 24/64 24/64 8/64 B(n,p)的分布列 3/4 1/64 9/64 27/64 27/64 0 1 对不同的P, 事件PX=x)发生的概率 上述估计思路体现的就是极大似然估计的思想方法: 在p所有可能的取值中选出能使样本观测值出现的概率为最 大的那一个来作为它的估计值
p是待估参数 在 p 所有可能的取值中选出能使样本观测值出现的概率为最 大的那一个来作为它的估计值. 今有放回抽球 3 次, 结 果得到两次白球, 试问如何估计袋中白球的个数? 解 设袋中有白球 m 个, ( ) (1 ) , k=0,1,2,3. 3 3 k k k P X k C p p 记X为抽得的白球数, 袋中白球数 0 1 2 3 4 p 0 1/4 2/4 3/4 1 抽到白球数 X x=0 x=1 x=2 x=3 1 0 0 0 27/64 27/64 9/64 1/64 8/64 24/64 24/64 8/64 1/64 9/64 27/64 27/64 0 0 0 1 例1(p.149例6) 袋中有黑球和白球共 4 个, 对不同的 p, 事件 P(X=x)发生的概率 对不同的 p, B(n,p)的分布列 则X~B(3, p), 3/4 27/64 上述估计思路体现的就是极大似然估计的思想方法: 则抽到白球的概率为 p = m /4

再如,设总体X服从B(1,B)分布, 即其分布列为 f(x;8)=P(X=x)=0x(1-03-,x=0,1 其中0(0<8<1)为未知参数,样本为X,…,Xn,样本值为x1,…,xm, 则事件(X1=x1,X=x2,…,X=xn)发生的概率为 L(0)=P(X1=x1,X2=x2,,Xn=xn) =f60)=10(1-9l=o含*(1-9)r客 i=l 对总体分布中的未知参数日进行估计时,既然观察结果X=x1, X2=x2,…,Xw=xn出现了,理应选取B使得事件(X=x1,X=x2,, X,=xm)发生的概率为最大.即用它作为0的估计值可使观察结果 出现的可能性最大 这种选择参数的估计量,使实验结果具有最大概率的思想就是极 大似然法的基本思想.即选取的估计量B应满足L(0)=maxL(0) 下面给出似然函数的定义和极大似然估计的求法
即用它作为 的估计值可使观察结果 出现的可能性最大. 这种选择参数的估计量, 使实验结果具有最大概率的思想就是极 大似然法的基本思想. 理应选取 使得事件 (X1=x1 , X2 =x2 ,„, Xn =xn ) 发生的概率为最大. 再如, 设总体 X服从 B(1, )分布, 下面给出似然函数的定义和极大似然估计的求法. 对总体分布中的未知参数 进行估计时, 即其分布列为 ( ) (1 ) , x 3 x P X x f (x;) x = 0, 1 其中(0< <1)为未知参数, 样本为 X1, „, Xn , 则事件 (X1=x1 , X2 =x2 ,„, Xn =xn ) 发生的概率为 样本值为 x1 , „, xn , n i i n n f x P X x X x X x 1 1 1 2 2 ( ; ) ( , , , ) n i i n i i x n x 1 (1 ) 1 n i x xi i 1 1 (1 ) L( ) = 既然观察结果 X1=x1 , X2 =x2 ,„, Xn =xn 出现了, 即选取的估计量 ^ ^ 应满足 L( )= max L( )

定义(P.148定义)设总体X的密度为f(x;8)(当X为离散型时 f(x;0)为分布列),0=(0,,…,01)是总体的未知参数,x1,2,xn 是样本X,X2,…Xn的一组样本值,则称 苑导麻烦1∥ L(0)=L(x1x2,,xn;0)=Πf(x;0) 转向nL(0)! 为样本的似然函数.若存在某个自=(⑨,2,,), 使得 L(x1x2,…,xn;0)=maxL(x12,…,n;0) 成立(其中⊙为参数空间),则称 即选取的估计量日应满足 0=X,X2,,Xm)=((X1,,Xn),2(X1,…,Xn),…,(X1,…,Xm), 为0的极大似然估计量.称 0=0(x1,x2,,xn=(A(1,,xn),(c1,,xn,…,0(x1,…,xn), 为B的极大似然估计值. ③ 如何求? L(0)是0的函数,可用求导的方法找到使L(0)达到最大值的0. 注意到lnL(0)为单增函数,故L(0)与InL(0)达到最大值的自 变量相同,故问题可转化为求IL(0)的最大值点
故 L( )与 lnL( )达到最大值的自 变量相同, 故问题可转化为求lnL( )的最大值点 . (当 X 为离散型时 f(x ; )为分布列), 定义(P.148定义) 设总体X 的密度为 f(x; ) x1, x2,„xn 是样本X1,X2,„Xn 的一组样本值, 则称 为样本的似然函数. =(1, 2,„, l)是总体的未知参数, f (xi; ) n i 1 L() L(x1 x2 , , xn ; ) 若存在某个 ), ˆ , , ˆ , ˆ ( ˆ 1 2 l 使得 ( , , ; ˆ) max ( , , ; ) 1 2 1 2 L x x xn L x x xn 成立(其中为参数空间), 则称 ( , , , ) ˆ ˆ X1 X2 Xn ( , , )), ˆ ( , , ), , ˆ ( , , ), ˆ ( 1 X1 Xn 2 X1 Xn l X1 Xn 为 的极大似然估计量. 称 ( , , )), ˆ ( , , ), , ˆ ( , , ), ˆ ( , , , ) ( ˆ ˆ x1 x2 xn 1 x1 xn 2 x1 xn l x1 xn 为 的极大似然估计值. 如 何 求 ? 即选取的估计量 ^ 应满足 L( )是 的函数, 可用求导的方法找到使 L( )达到最大值的 . 求导麻烦!! 转向lnL( )!! 注意到lnL( )为单增函数, ① ② ③

求极大似然估计的一般步骤是: ①由总体分布建立似然函数L(θ)=广f(x;0) 一一把自变量x看 成常数,把未知参数0=(0,凸,…,01)看成自变量; ②求似然函数L()的最大值点 一一转化为求nL()的最大值 点,即 1建立似然方程组: In L()=0 (i=1,2,…,l), a0: 2解似然方程组得到L(0)的最大值点; ③ 将样本X,X2,…X代入最大值点的表达式中,就得未知参数 的极大似然估计量,将样本值x1,x2,x代入最大值点的表达式 中,就得未知参数的极大似然估计值. 是实数时,似然方程组就是方程 dinL()=0. do 下面举例说明如何求极大似然估计
将样本值 x1, x2,„xn 代入最大值点的表达式 中, 就得未知参数的极大似然估计值 ˆ . ——把自变量x看 成常数, 把未知参数 =(1, 2,„, l)看成自变量; —— 转化为求ln L( )的最大值 点, ①由总体分布建立似然函数 L( ) ② 求似然函数 L()的最大值点 求极大似然估计的一般步骤是: ③ 将样本 X1,X2,„Xn 代入最大值点的表达式中, 就得未知参数 的极大似然估计量 ˆ , n i f xi 1 ( ; ) 即 1 0 建立似然方程组: 0 ( 1 2 ) , ln ( ) i , , ,l L i 2 0 解似然方程组得到 L( )的最大值点; 0 . ln ( ) d 是实数时, 似然方程组就是方程 d L 下面举例说明如何求极大似然估计

例1(P.147例5)设总体X~B(1,p),其分布列为 P(x;p)=px(1-p)1-x,x=0,1, 1,0,0,1,0,0是取自总体的一组样本值,求参数p的极大似然估计. 解样本的似然函数为:L(p)=P(x;p)=Ⅱp(1-p)-x i=1 i=1 对数似然函数为:lnL(p)=名xlnp+合(1-x)l血(I-p) 名x血p+(m-名x)n(1-p) = 对p求导并令其为0得似然方程:D-产-a-名 0=0 解之得p的极大似然估计量:方=名X,=灭, 代入样本值即得极大似然估计值为:=1+0+0+1+0+0)=号·
求参数 p 的极大似然估计. n i L p P xi p 1 解 样本的似然函数为: ( ) ( ; ) ln ( ) ln (1 )ln(1 ) 1 1 L p x p xi p n i n i i ( ; ) (1 ) , 0, 1, 1 P x p p p x x x 例1(P.147 例5) 设总体 X ~ B(1, p), 1, 0, 0, 1, 0, 0 是取自总体的一组样本值, 其分布列为 n i xi xi p p 1 1 (1 ) 对数似然函数为: ln ( )ln(1 ) 1 1 x p n x p n i i n i i 对 p 求导并令其为0 得似然方程: ( ) 1 ln ( ) 1 1 1 1 n i i n i i n x p x dp p d L p = 0 , , 1 ˆ 1 X X n p n i i 解之得 p 的极大似然估计量: 代入样本值即得极大似然估计值为: . 3 1 (1 0 0 1 0 0) 6 1 p ˆ

例2.165续)设总体X的密度为fx;)= 其它, 其中2>0为未知参数,X,X2,…,Xm是取自总体X的一组样本, 求2的极大似然估计量与矩估计量. 5,动-20-12 解(1)样本的似然函数为 0 其他. 当x>0时,L(2)>0,1≤i≤n, 故有对数似然函数:nL(a)=nln元-元公x, i=l 对乳求导并令其为0可得似然方程: nL(2=- d =0, 解得极大似然估计量:元=n会X=是 (2)EX=xfx;2)dx=1/2, 令克=名x,=X, 解得矩估计量:元=支
0 , . , 0, 1 2, , ; 1 其他 e xi i , n n i xi 解(1) 样本的似然函数为 n i xi L f 1 () ( ; ) , 1 n i n xi e EX xf x dx ( ; ) 当 xi>0 时, L()> 0, ( ) ln , ln 1 n i L n xi 1 i n, X1, X2, „, Xn 是取自总体X的一组样本, 0, , , 0 ( ; ) 其它 e x ; f x x 求的极大似然估计量与矩估计量. 其中> 0为未知参数, 例2(P.165 练9) 设总体X 的密度为 故有对数似然函数: n i xi n d d L 1 ln ( ) 对 求导并令其为0 可得似然方程: = 0, 解得极大似然估计量: n i n Xi 1 ˆ 令 , 1 1 1 X X n n i i (2) = 1/ , 解得矩估计量: . 1 ˆ X ; 1 X

例3P.150例7)设总体X~N(山,σ2),其中μ,o2均未知,设 X,X2,…Xn是取自X的一个样本.求4与o2的极大似然估计量. 解样本的似然函数为 --42 Uaa=9:o=42oe 2o2 故有对数似然函数n4,o2)=-号n2mo2-20名x-四' 对u和o分别求偏导并令其为0得似然方程组: 估计的 8o=名(,-川=0 Oμ 注意到σ2是o的函数! 不变性 alnL(w,σ2)=- 0o (-=0, ,+ 62=(6)2 解之得极大似然估计量 x=尾, n 6=含X-4=B,6=日2-, 正态分布:极大似然估计量== 矩估计量
设 X1,X2,…Xn 是取自 X 的一个样本. 解 样本的似然函数为 其中 , 2 均未知, 求 与 2 的极大似然估计量. n i xi L f 1 2 2 (, ) ( ; , ) 例3(P.150 例7) 设总体X ~ N(,2), n i xi e 1 2 ( ) , 2 1 2 2 故有对数似然函数 n i xi n L 1 2 2 2 2 ( ) 2 1 ln 2 2 ln ( , ) , 1 ˆ 1 X X n n i i 解之得极大似然估计量 1 ( ) 0, ln ( , ) 1 2 2 n i xi L 对 和2 分别求偏导并令其为 0 得似然方程组: ( ) 0 , 2 1 2 ln ( , ) 1 2 2 2 4 2 n i xi L n n i Xi n 1 2 2 ( ) 1 ˆ 2 3 , ( ) 1 ˆ 1 2 n i xi n = B2 , 2 2 ˆ ( ˆ ) 估计的 不变性 注意到2是 的函数 ! 正态分布:极大似然估计量 === 矩估计量

可证明极大似然估计具有下面的单调函数不变性: 若0为未知参数0的极大似然估计量,而g(0)为0的单调函数, 则g(0)也是g(0)的极大似然估计量. 例4一罐中装有白球和黑球,有放回地抽取一个容量为的样本, 其中有k个白球,求罐中黑球与白球之比R的极大似然估计. 解设X,&,,出为所取样本,X,=取到白球 i=1,…,m 0,取到黑球 则X,…,Xm~B(1,p),p是每次抽取时取到白球的概率,且p未知 容易求得n的极大似然估计为:方=合,:R=号, 由极大似然估计的不变性知R的极大似然估计是=2=冬-1. 上述解法是应用微积分中的技巧求似然函数L()的最大值点. 但当似然函数L()不可微或偏导数不为零时,就不能用上述求导 方法求未知参数的极大似然估计了.这时要用极大似然原则来求
可证明极大似然估计具有下面的单调函数不变性: 而 g( )为 的单调函数, 则 ^ g( ) 也是 g( )的极大似然估计量. 若 ^ 为未知参数 的极大似然估计量, 例4 一罐中装有白球和黑球, Xi i 1,,n 0, 1, 取到黑球 取到白球 解 设 X1, X2 , „, Xn 为所取样本, 则 X1,„, Xn ~B(1, p), 有放回地抽取一个容量为n的样本, 其中有k个白球, 求罐中黑球与白球之比R的极大似然估计. p是每次抽取时取到白球的概率, 且 p未知. ˆ , n k p p p R ˆ 1 ˆ ˆ 1 . k n 容易求得 p 的极大似然估计为: 由极大似然估计的不变性知 R 的极大似然估计是 , 1 p p R 就不能用上述求导 方法求未知参数的极大似然估计了. 上述解法是应用微积分中的技巧求似然函数L( )的最大值点. 但当似然函数 L()不可微 这时要用极大似然原则来求. 或偏导数不为零时