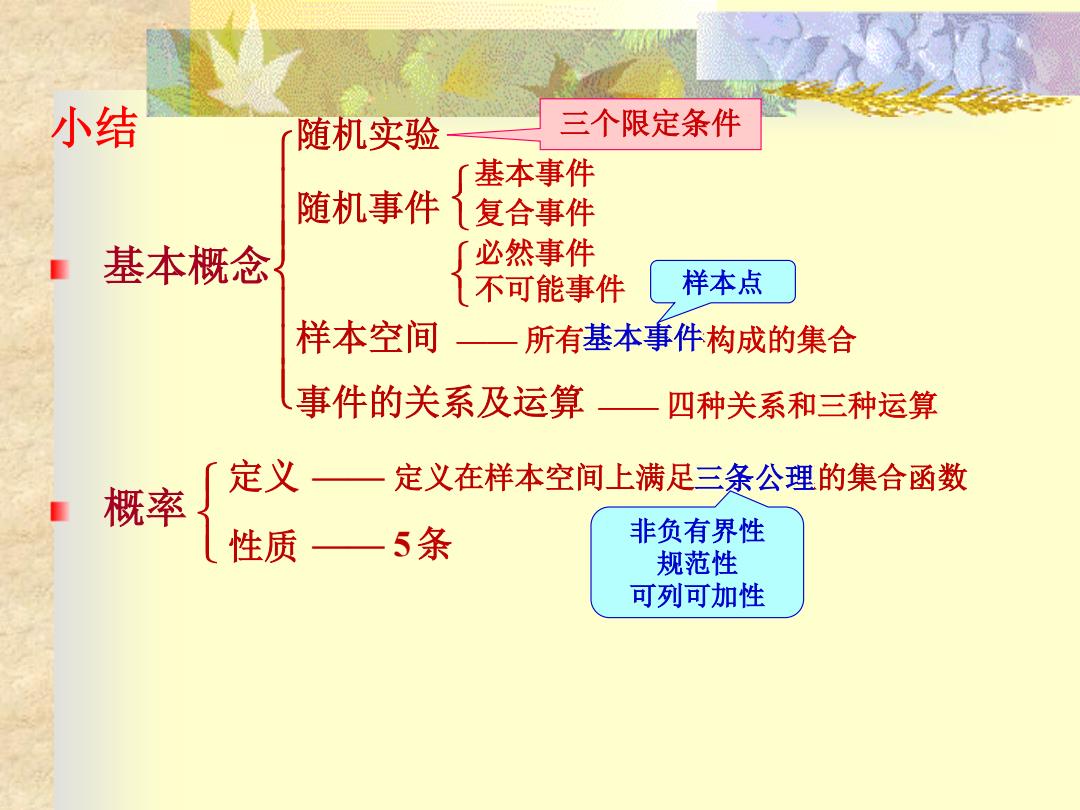
小结 随机实验 三个限定条件 基本事件 随机事件1复合事件 基本概念 必然事件 不可能事件 样本点 样本空间 所有基本事件构成的集合 事件的关系及运算 四种关系和三种运算 定义— 定义在样本空间上满足三条公理的集合函数 概率 性质一5条 非负有界性 规范性 可列可加性
随机实验 随机事件 样本空间 事件的关系及运算 小结 基本概念 概率 基本事件 复合事件 必然事件 不可能事件 三个限定条件 —— 所有基本事件构成的集合 —— 四种关系和三种运算 定义 —— 5条 —— 定义在样本空间上满足三条公理的集合函数 基本事件 样本点 三条公理 非负有界性 规范性 可列可加性 性质

用概率的公理化定义,从实验出发直接计算P(A)是 困难的,甚至是不可能的 某些满足特定条件的实验可以直接计算. 基本事件的发生具有等可能性 §1.2.4等可能概型 一、古典概型 定义若随机试验E具有以下两个特征: (1)E的样本空间只有有限多个样本点,即2={o,02,…,⊙n}; (2) 试验中每个样本点出现的可能性相同, 则称E为古典概率模型,简称古典概型 有限等可能随机试验 古典概型中事件概率的计算?
用概率的公理化定义,从实验出发直接计算 P(A)是 困难的, 某些满足特定条件的实验可以直接计算 . 基本事件的发生具有等可能性 §1.2.4 等可能概型 一、古典概型 定义 若随机试验 E 具有以下两个特征: (1) E 的样本空间只有有限多个样本点, (2) 试验中每个样本点出现的可能性相同, 即 {1 ,2 , ,n }; 则称E 为古典概率模型,简称古典概型 . 有限等可能随机试验 古典概型中事件概率的计算? 甚至是不可能的

由于2={o,}+{o2}+…+{0n} ∴.1=P(2)=P(o1)+P(o2)+·+P(on), 又由于各样本点出现的可能性相同, .P(@,)=i=l,2,,n 设事件A由k个样本点组成,即A={0i1,02,,0i}, 由可加性知A的概率为: P八4)=片=食的联本点数 2中的样本点总数 称此概率为古典概率.这种确定概率的方法称为古典方法. 这样就把求概率问题转化为计数问题. O
这样就把求概率问题转化为计数问题 . 设事件 A由 k个样本点组成 ,即 称此概率为古典概率. 这种确定概率的方法称为古典方法 . 由于 1 2 { } } { } { n 1 P() P(1) P(2 ) P(n), 又由于各样本点出现的可能性相同, , 1,2, , ; 1 ( ) i n n P i 由可加性知 A的概率为: { , , , }, A i1 i 2 i k ( ) ( ) ( ) P i 1 P i 2 P ik n k A 包含的样本点数 中的样本点总数 中的样本点总数 包含的样本点数 A n k P(A)

例1 同时掷两枚均匀硬币,分别求事件A={两枚都出现正 面},B={一枚出现反面}和C={两枚都出现反面}的概率. 解 同时掷两枚硬币有4个等可能的结果,即样本空间为 2={(正,正),(正,反),(反,正),(反,反)月古典概型 又事件A,B,C分别包含1个、2个和1个样本点, PA0=P(=子= ;PC=} 列举法 排列组合是计算古典概率的重要工具 这里我们先简要复习一下计算古典概率所要用到的基本计数原理
同时掷两枚均匀硬币,分别求事件A={两枚都出现正 面}, B={一枚出现反面} 和 C={两枚都出现反面}的概率. 解 同时掷两枚硬币有4个等可能的结果,即样本空间为 例1 ={(正,正), (正,反), (反,正), (反,反)} 4个等可能 古典概型 又事件A, B, C 分别包含 1个、2个和 1个样本点, ; 4 1 P(A) ; 2 1 4 2 P(B) . 4 1 P(C) 排列组合是计算古典概率的重要工具 列 举 法 这里我们先简要复习一下计算古典概率所要用到的基本计数原理

1.加法原理 设完成一件事有种方式,无论通过哪种方式都可以完成这件事, 第1种方式有n1种方法,第2种方式有n2种方法,…;第m种方式有nm种方法, 则完成这件事共有n1+2+…+nm种不同的方法 2.乘法原理 设完成一件事有个步骤,必须通过每一步骤,才算完成这件事, 第1个步骤有种方法,第二个步骤有n2种方法,·;第m个步骤有nm种方法, 则完成这件事共有1×n2×…×nm种不同的方法 这两个计数原理不但可直接解决不少具体问题,也是推导下面常用排列组合公式的基础 排列组合的公式 选排列 A=n(n-1)(n-2)…(n-k+1)= n! (n-k): A的=C·k! 1.排列 全排列 Ag=An=n(n-1)(n-2)…21=n: 允许重复的排列n·n…n=nk 组合不管顺序 2.组合 Ch=4= n! k (n-k)!k!
第1个步骤有n1种方法, 第二个步骤有n2种方法, „ ; 第m个步骤有nm种方法, 1. 加法原理 设完成一件事有m种方式,无论通过哪种方式都可以完成这件事, 第1种方式有n1种方法, 第2种方式有n2种方法,„ ; 第m种方式有nm种方法, 则完成这件事共有 n1 + n2 + „ + nm 种不同的方法 2. 乘法原理 设完成一件事有m个步骤, 必须通过每一步骤, 才算完成这件事, 则完成这件事共有 n1 n2 „ nm 种不同的方法 这两个计数原理不但可直接解决不少具体问题, 也是推导下面常用排列组合公式的基础 . 1. 排列 2. 组合 排列组合的公式 ( )! ! ( 1)( 2) ( 1) n k n A n n n n k k n A An n(n 1)(n 2) 2 1 n! n n k n nn n ( )! ! ! ! n k k n k A C k k n n A C k! k n k n 选排列 全排列 允许重复的排列 组合不管顺序

例2(P.12例3)一个盒子中装有10个大小、形状完全相同的晶体管, 其中3只是次品.按下列两种方法抽取晶体管: (1)先任取一只,作测试后放回盒中,再任取下一只,二 有放回抽样 (2)先任取一只,作测试后不放回,在剩下的中再任取一只. 试分别对这两种抽样方法,求从这10只晶体 无放回抽样 管任取2只中,恰有一只是次品的概率. 解设A={抽取的2只晶体管中恰有一只是次品} (1)有放回抽样:由于每次都是从10只中取一10×10种取法 即2的样本点数n=102, 古典概型 一共有7×3+3×7=42种取法 P()=42 100 (2)无放回抽样:第1次是从10只中取,第2次是从9只中取, 即2的样本点数n=10x9,古典概型 10×9种取法 A一共有7×3+3×7=42种取法 P(A= 90
(2)先任取一只, 作测试后不放回, 在剩下的中再任取一只. 一个盒子中装有10个大小、形状完全相同的晶体管, 其中 3 只是次品. 例2 (P.12 例3) 按下列两种方法抽取晶体管: (1)先任取一只, 作测试后放回盒中, 再任取下一只; 有放回抽样 试分别对这两种抽样方法, 求从这10只晶体 无放回抽样 管任取2 只中,恰有一只是次品的概率. 解 设 A={ 抽取的 2 只晶体管中恰有一只是次品} (1)有放回抽样: 由于每次都是从10只中取 —— 1010 种取法 即 的样本点数 n= 102 , 第 1次取到合格品,且第2 次取到次品 第1次取到次品,且第2 次取到合格品 A: —— 7 3 —— 3 7 —— 共有 73 + 37 = 42 种取法 古典概型 . 100 42 P(A) (2)无放回抽样: 第1次是从10只中取, 第2次是从9只中取, 即 的样本点数 n= 109, —— 109 种取法 A:—— 共有 73 + 37 = 42 种取法 古典概型 . 90 42 P(A)
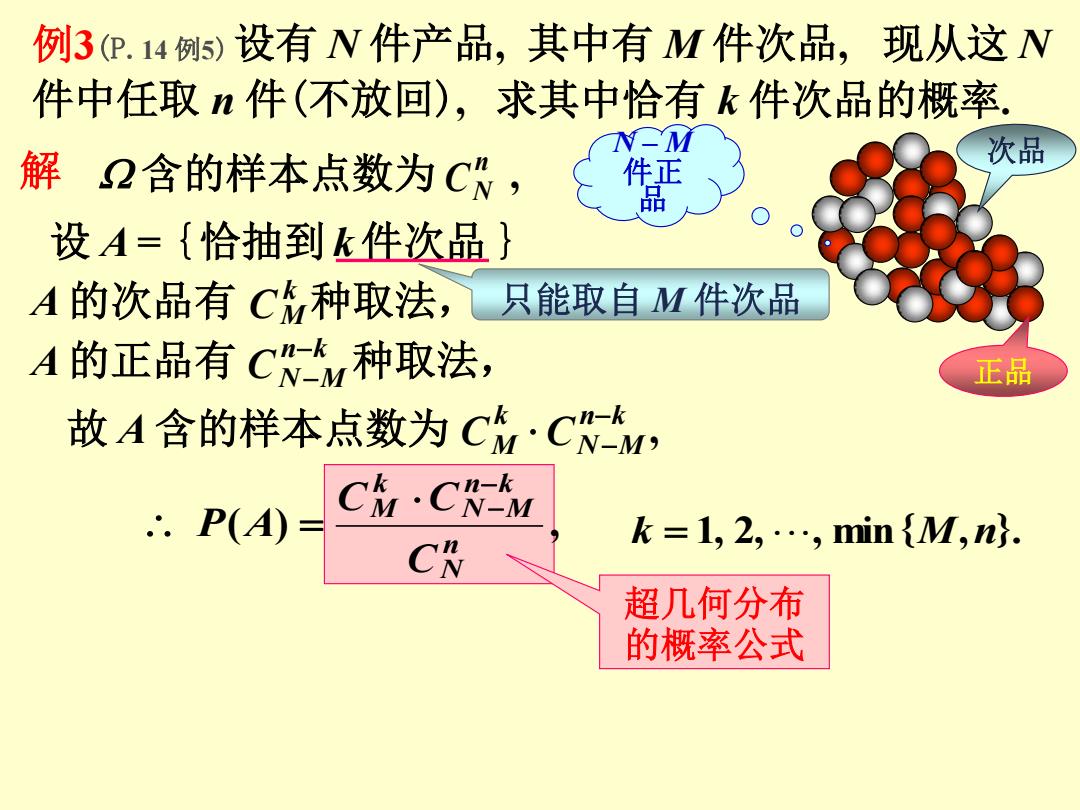
例3P.14例)设有N件产品,其中有M件次品,现从这N 件中任取n件(不放回),求其中恰有k件次品的概率. N- 解2含的样本点数为C, 次品 品 设A={恰抽到k件次品} A的次品有C种取法,只能取自M件次品 A的正品有CM种取法, 正品 故A含的样本点数为C·CM, ∴.P(A)= C·CM k=1,2,…,min{M,n. 超几何分布 的概率公式
现从这 N 件中任取 n 件(不放回), 设有 N 件产品, 其中有 M 件次品, 解 ( ) , n N n k N M k M C C C P A 例3(P.14 例5) 设 A = {恰抽到 k件次品 } 求其中恰有 k 件次品的概率. 次品 正品 N – M 件正 品 含的样本点数为 , n C N A 的次品有 C M k 种取法, 只能取自 M 件次品 A 的正品有 C N n k M 种取法, 故 A 含的样本点数为 , n k N M k CM C k 1, 2, , min{M,n}. 超几何分布 的概率公式

例4 在电话号码簿中任取一个电话号码,求后面4个 数字全不同的概率(设后面4个数中的每一个数都是等可能地取 自0-9这10个数). 允许重复 解所求概率与号码的位薮无关,2含样本点数:104, 设A={后4位数字全不相同}, 从10个不同数字中 A所含样本点数为A0, 取4个的排列 ·P(A= A10 =0.504. 104 求样本空间样本点总数和求事件所含样本点数的计数方法不同
在电话号码簿中任取一个电话号码,求后面4个 数字全不同的概率(设后面 4个数中的每一个数都是等可能地取 自 0-9 这10个数). 解 所求概率与号码的位数无关, 允许重复 求样本空间样本点总数 和 求事件所含样本点数 的计数方法不同 从10个不同数字中 取4个的排列 例4 设 A={ 后4 位数字全不相同 }, 含样本点数: 10 4 , A所含样本点数为 , 4 A10 0. 504. 10 ( ) 4 4 10 A P A

再次提醒注意: 1、在应用古典概型时必须注意“等可能性”的条件 例5 掷两枚骰子出现的点数之和等于3的概率, 解 掷两枚骰子出现的点数之和的可能数值为 2,34,…,12}, .PA× 2={(1,1),(1,2(2,1,(1,3),…,(6,6)} P(0= 2 1 6×618· “等可能性”是一种假设,在实际应用中,我们需要根据 实际情况去判断是否可以认为各基本事件或样本点是等可能的 在实际应用中,往往只能“近似地”出现等可能,“完全 地”等可能是很难见到的许多场合,由对称性和均衡性,我们 就可以认为基本事件是等可能的并在此基础上计算事件的概率. 2、用排列组合公式计算样本点数时必须注意不要重复计数,也 不要遗漏 3、所求为“至少”或“至多”的问题,用余概公式简单
P(A)= —— “等可能性”是一种假设,在实际应用中,我们需要根据 实际情况去判断是否可以认为各基本事件或样本点是等可能的. 1、在应用古典概型时必须注意“等可能性”的条件 再次提醒注意: 在实际应用中,往往只能“近似地”出现等可能,“完全 地”等可能是很难见到的在许多场合,由对称性和均衡性,我们 . 就可以认为基本事件是等可能的并在此基础上计算事件的概率. 2、用排列组合公式计算样本点数时必须注意不要重复计数,也 不要遗漏 例5 掷两枚骰子出现的点数之和等于3 的概率. 解 掷两枚骰子出现的点数之和的可能数值为{2, 3, 4, „, 12}, . 11 1 P(A) ={(1,1), (1,2), (2,1), (1,3), „ , (6,6) } 2 66 . 18 1 3、所求为“至少”或“至多”的问题,用余概公式简单
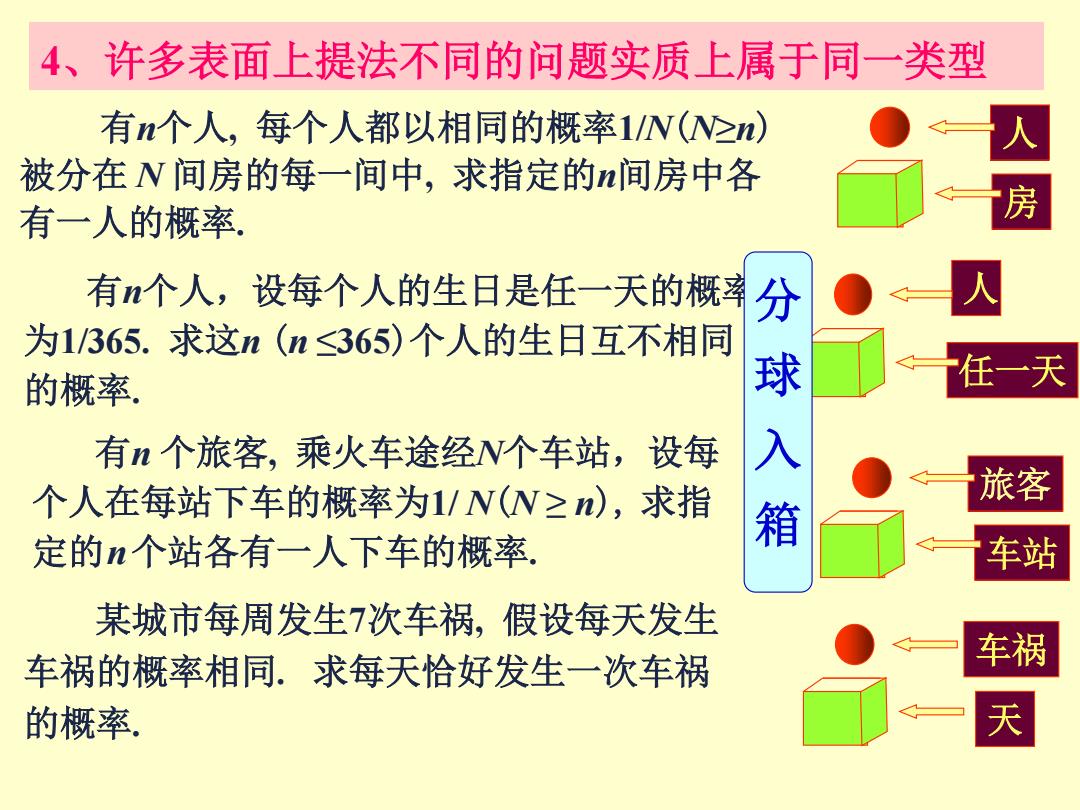
4、许多表面上提法不同的问题实质上属于同一类型 有n个人,每个人都以相同的概率1/N(N>n) 人 被分在N间房的每一间中,求指定的n间房中各 有一人的概率 房 有n个人,设每个人的生日是任一天的概幸 为1/365.求这n(n≤365)个人的生日互不相同 的概率. 分球 任一天 有n个旅客,乘火车途经N个车站,设每 个人在每站下车的概率为1/N(N≥n),求指 入箱 旅客 定的n个站各有一人下车的概率. 车站 某城市每周发生7次车祸,假设每天发生 车祸的概率相同.求每天恰好发生一次车祸 车祸 的概率. 天
有n个人, 每个人都以相同的概率1/N(N≥n) 被分在 N 间房的每一间中, 求指定的n间房中各 有一人的概率. 人 房 4、许多表面上提法不同的问题实质上属于同一类型 有n个人,设每个人的生日是任一天的概率 为1/365. 求这n (n ≤365)个人的生日互不相同 的概率. 人 任一天 有n 个旅客, 乘火车途经N个车站,设每 个人在每站下车的概率为1/ N(N ≥ n), 求指 定的n个站各有一人下车的概率. 旅客 车站 某城市每周发生7次车祸, 假设每天发生 车祸的概率相同. 求每天恰好发生一次车祸 的概率. 车祸 天 分 球 入 箱