上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）09、多维随机变量及分布 §3.5 二维随机变量函数的分布

复习X与Y的联合分布F(x,y)=P{X≤x,Y≤y} 分布 离散型F(x,y)=PX≤七，Y≤y}=∑P xi≤，ys 函数1 连续型F(x,y)=∫.f(u,)u (X,)关于X和Y的边缘分布Fx(x)=F(x,+o),Fy(y)=F(+o,y) 边缘 离散型 关于X的P=月P=P(X=x,Fx()2P x:≤x 关于Y的 分布 连续型 关于X的fx(x)=fc,y),Fx(x)=」f(u,y)d 关于Y的 P过 二维随机变量的条件分布 离散型P{X=x,Y=y}= 连续型fwxI)=f” Fnxn=Cfu恤， fr(y) f(x,y)=fxr(xly).fy(y) X与Y相互独立P(XKx,Y≤y)=P(X≤x)·P(Y≤y)F(c,y)=Fx(x)F,(y) 离散型 p=pi。Pj, P(X=xilY=y}=Pi.,P{Y=yiX=x}=p.j 连续型fx,y)=fx(x)f(y), fxir(xy)=fx(x),fyx(yx)=fy(y) 独立随机变量X,Y的连续函数g1(X),g2(Y)仍是独立的随机变量 例如：X与Y独立→X+b与er独立

复习 分布 函数    离散型 连续型        x x y y ij i j F x y P X x Y y p , ( , ) { , }    y x F(x, y) f (u,v)dudv 边缘 分布    离散型 连续型 ( ) ( , ) ,    f X x  f x y dy X 与Y 的联合分布 F(x, y)  P{X x, Y  y} (X,Y)关于X 和Y 的边缘分布 F (x)  F(x,), X F ( y) F( , y) Y   关于X 的 关于Y 的 关于X 的 关于Y 的 { }, 1 i j i ij p   p  P X  x        x x X i i F ( x) p       x FX (x) [ f (u, y)dy]du 二维随机变量的条件分布 离散型 连续型 { | } , j ij i j p p P X x Y y     , ( ) ( , ) | ( | ) f y f x y f x y Y X Y  ( , ) , f (x, y)  f X|Y (x | y) fY ( y) ( ) 1 ( ) f u y du f y F x y x Y X Y      X 与 Y 相互独立 P(X x, Y  y)  P( X x)  P(Y  y ) F(x, y) F (x)F ( y)  X Y , pij pi  p j   f (x, y)  f X (x) fY ( y), j i j i j i P X x Y y p P Y y X x p {  |  }   , , {  |  }  f (x y ) f (x), f ( y x ) f ( y)  X Y  X Y X  Y   离散型 连续型 独立随机变量X,Y的连续函数g1(X),g2(Y)仍是独立的随机变量 例如： X 与Y 独立  aXb与 e Y 独立

§3.5二维随机变量函数的分布 我们曾经讨论了一维随机变量X函数g()的分布， 独立随机变量的连续函数g1(x),,gn(x)仍独立 现在我们进一步讨论： 当随机变量X,X2,,Xn的联合分布已知时， 如何求出它们的函数 y=8X,X2,…X)j=1,2,…m的联合分布？ 我们集中讨论两个随机变量的函数的分布问题 二维随机变量X,)的分布 维随机变量Z的分布 和二元函数Z=g(X,) 我们仍采取类比的方法学习二维随机变量函数的分布问题 分两种情形讨论

我们仍采取类比的方法学习二维随机变量函数的分布问题 我们曾经讨论了一维随机变量 X 函数 g(X) 的分布， 我们集中讨论两个随机变量的函数的分布问题 当随机变量X1, X2, …, Xn 的联合分布已知时， §3.5 二维随机变量函数的分布 现在我们进一步讨论: 如何求出它们的函数 Yj = gj (X1, X2, …,Xn) j =1,2,…,m 的联合分布? 二维随机变量(X,Y)的分布 和二元函数 Z= g(X, Y)  一维随机变量 Z 的分布    分两种情形讨论 独立随机变量的连续函数 g1 (x1 ),…, gn ( xn ) 仍独立

一、离散型随机变量函数的分布 -1 1 仍从实例中总结一般方法： 1/4 1/8 例1(P.85例1)已知(X,Y)的联合分布列 1 1/4 3/8 求（1)Z=X+Y的分布列； (2)Z=X/Y的分布列. 解(1)Z=X+Y可能的取值为-2,0,2， Z -2 0 2 P(Z=-2)=P(X=-1,Y=-1)=1/4; Pk 1/4 3/8 3/8 P(Z=0)=P(X=-1,Y=1)+PX=1,Y=-1)=3/8; P(Z=2)=P(X=1,Y=1)=3/8; Z -1 1 (2)Z2=XY可能的取值为-1,1， Pk 3/8 5/8 P(Z=-1)=P=-1,Y=1)+PX=1,Y=-1)=3/8; P(Z=1)=P(X=-1,Y=-1)+PX=1,Y=1)=5/8

例1(P.85 例1) 已知(X,Y )的联合分布列 解 (1) 一、离散型随机变量函数的分布 求 (1) Z = X+Y 的分布列； (2) Z= X/ Y 的分布列. X -1 1 1/4 1/4 Y -1 1 1/8 3/8 Z = X+Y 可能的取值为 -2, 0, 2, P(Z=-2) = 1/4 ; Z pk -2 0 2 = P(X=-1,Y=1)+P(X=1,Y=-1) P(Z=-1) 1/4 Z pk -1 1 = 3/8 ; P(Z=1)= P(X=-1,Y=-1)+P(X=1,Y=1) 3/8 = 5/8 . 5/8 P(Z=0) 3/8 P(Z=2) 3/8 (2) Z2 = X/Y 可能的取值为 -1, 1, 仍从实例中总结一般方法： =2 = P(X=-1,Y=-1) = 3/8 ; = 3/8 ; =-0 2 =-1 = P(X=-1,Y=1)+P(X=1,Y=-1) = P(X=1,Y=1)

例2 今有两封信欲投入编号为A,B,C的3个邮筒，设X,Y 分别表示投入邮筒A号和B号的信的数目，试求： (1)X,)的分布列； (2)求=min{X,Y}的分布列. 解(1)由题意可知X和Y取值均为0,1,2， 2 P(X=0,Y=0上P(两封信均投入C邮号筒)= 32 0 1/9 2/9 1/9 P(K0,=I)=P(一封投入C筒，另一封投入B筒)=是： 2/9 2/9 0 32 P(X0,Y=2)=P(两封都投入B筒)=；…， 2 1/9 0/9 0 (2)V的可能取值为0,1， P(V-0)-P(mim(X,r)-0)-P(X-0.Y-j)+P(X-i.Y-0)-g: =0 PV=)=P(mim(X,)=1)=1-子=号； 最后写出V的分布列即可

设 X,Y 分别表示投入邮筒A号和B号的信的数目， 解 (1)           2 1 2 0 ( 0, ) ( , 0) j i P X Y j P X i Y 例2 今有两封信欲投入编号为A,B,C 的3个邮筒， 试求： (1) (X,Y)的分布列； (2)求 V=min{X,Y}的分布列 . P(X=0,Y=1) ; 3 1  2 ; 3 2 1 C2  P(V 0)  P(min(X,Y)0 ) P(V1)  P(mi n(X,Y) 1) 9 7  1 由题意可知X和Y取值均为 0, 1, 2， ; 9 7  (2) V 的可能取值为 0, 1， P(X0, Y0) 1/9 2/9 1/9 X 0 1 2 Y 0 1 2 ……， 最后写出 V 的分布列即可. = P(两封信均投入C邮号筒) =P(一封投入C筒, 另一封投入B筒) P(X=0,Y=2)=P(两封都投入B筒) ; 3 1  2 2/9 1/9 2/9 0 0/9 0 ; 9 2 

二、连续型随机变量函数的分布 设连续型随机变量X,Y)的概率密度为f(x,y), 其函数Z=g(X,Y)为连续函数， 求连续型随机变量Z的概率密度fz(亿)？ (I)求Z的分布函数Fz(z)； 构成的区域记为G Fz(a)=P(Z≤z)=P(gK,Y)≤z)=P(X,)∈G)=jf(x,) Fz(z)=J∬f(x,y)y 8(x,y)≤z () 对分布函数F,(z)求导即得Z的概率密度fz(2). 下面就按着这个思路，讨论几个特殊函数的分布： 分布函数法

二、连续型随机变量函数的分布 设连续型随机变量(X,Y )的概率密度为 f ( x , y) ， 其函数Z= g(X,Y) 为连续函数, 求连续型随机变量 Z的概率密度 fZ (z )？ (I) 求 Z 的分布函数 FZ(z)； (II) 对分布函数 FZ(z)求导即得 Z 的概率密度 fZ (z) . ∵FZ(z)= P(Zz ) = P( g(X,Y)z ) 构成的区域记为G   ( , ) . G = P((X,Y)G ) f x y dxdy     g x y z FZ z f x y dxdy ( , ) ( ) ( , ) 下面就按着这个思路, 讨论几个特殊函数的分布： 分布函数法

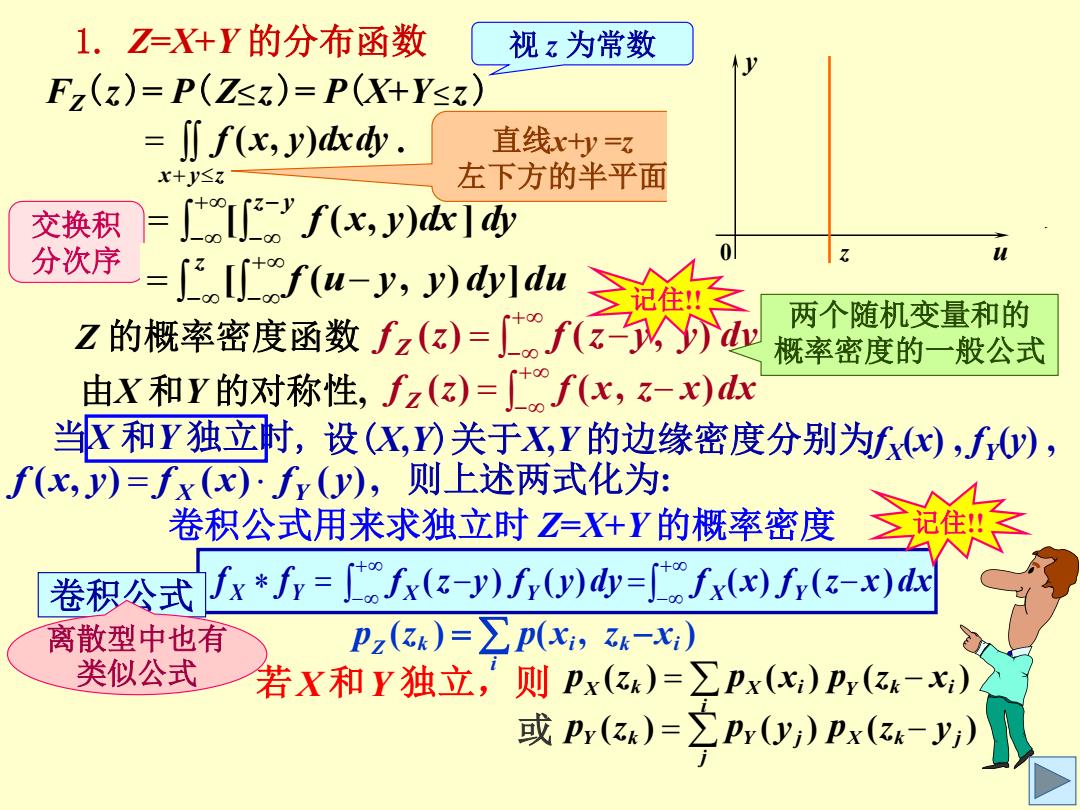
1.Z=X+Y的分布函数 视z为常数 F,（z)=P(Zsz)=PX+Y≤z) =∬f(x,y)dky. 直线x+y=乙 x+y≤z 左下方的半平面 交换积 =f'f(x,y)] 分次序 =fu-八，)d三条 Z的概率密度函数fz(z)=f(z个)dm 两个随机变量和的 概率密度的一般公式 由X和Y的对称性，fz(z)=f(x,z-x)x 当驱和Y独立时，设(X,)关于X,Y的边缘密度分别为fx),fy), f(x,y)=fx(x)f(y),则上述两式化为： 卷积公式用来求独立时Z=X+Y的概率密度 卷积公式∫x*乐=」fx(亿-y)f0)d=∫fx(x)f(a-x)瓜 离散型中也有 Pz(zk)=∑p(x,k-x) 类似公式 若X和Y独立，则Px(z)=∑Px(x Py(Zk-xi) 或P(x)=2P,)Px(-)

当X 和Y 独立时, 令x=u–y ( , ) .     x y z f x y dxdy 1. Z=X+Y 的分布函数 FZ(z)= P(Z≤z)= P(X+Y≤ z )         f x y dx dy z y [ ( , ) ] x+y  z    z y f (x, y)dx 0 X Y    z f (u y, y)du   z f (u y, y)du f z f z y f y dy f x f z x dx Z  X Y  X Y       ( )  (  ) ( )  ( ) (  ) 直线x+y =z 左下方的半平面 设(X,Y)关于X,Y 的边缘密度分别为fX (x) , fY (y) , f (x, y) f (x) f ( y), 则上述两式化为: X Y   卷积公式用来求独立时 Z=X+Y 的概率密度 x+y = z 0 z u y 由概率密度与分布函数的关系: F(x) f (t)dt , F (x) f (x) x      Z 的概率密度函数 f z f z y y dy Z     ( )  (  , ) f Z z  f x z x dx    由X 和Y 的对称性, ( )  ( ,  ) 两个随机变量和的 概率密度的一般公式 卷积公式 f X  f Y  离散型中也有 类似公式 记住!! 记住!! [ ]dy      交换积 分次序 视 z 为常数    i pZ (zk ) p(xi , zk xi ) 若X 和Y 独立，则    i pX (zk ) pX (xi ) pY (zk xi )    j 或 pY (zk ) pY ( yj ) pX (zk yj ) f u y y dy du z [ ( , ) ]       

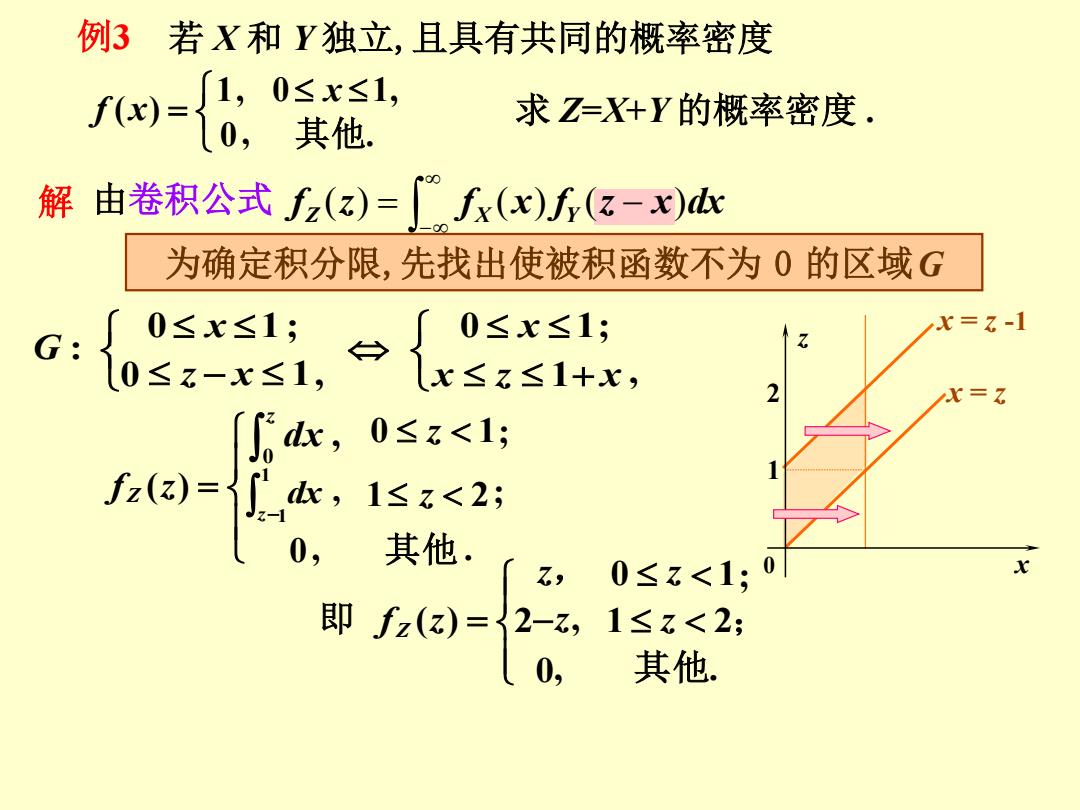
例3 若X和Y独立，且具有共同的概率密度 w= 求Z=X+Y的概率密度. 其他. 解由卷积公式fz(z)=fx(x)f(z-r) 为确定积分限，先找出使被积函数不为0的区域G G: 0≤x≤1； 0≤x≤1； X=z-1 0≤z-x≤1， x≤z≤1+x, 2 x=Z [6c,0≤z<l; fz(3)=d,1≤z<2; 0,其他. z,0≤z<1:0 x 即fz()={2-z, 1≤z<2; 0, 其他

        0 1; ( ) z f Z z 为确定积分限,先找出使被积函数不为 0 的区域G 若 X 和 Y 独立,且具有共同的概率密度 求 Z=X+Y 的概率密度 .       0, . 1, 0 1, ( ) 其他 x f x    由卷积公式 f Z (z)  f X (x) f Y (z  x)dx         0 1, 0 1 ; : z x x G          1 , 0 1; x z x x 例3 解  z dx 0 , x = z -1 2 x = z 1 0 x z 1 z  2; 0, 其他 .   1 1 , z dx           0, . 2 , 1 2 0 1; ( ) 其他 ； ， 即 z z z z fZ z

例4(P.89例5)若X和Y相互独立，且均服从N(0,1),求Z=X+Y的密度. 解fx(x)=D 2, -0<X<+00; 2π f0)=2ze,-<y<+o 由卷积公式 f,f,k-=2eek元 d 2元J- 均匀分布？ e=2元e.Z服从正态分布N0,2. 类似地可以证明： 若X和Y独立，且X~N(4,o),Y~N(42,o), 泊松分布、·二项分布 也有相应结论 → Z=X+Y~N(41+42,o1+o) 此结论推广到个独立的正态随机变量之和的情形请自行写出结论 更一般地，可以证明：若X;~N(4,O),且X1,X2,…,Xn独立，则 2aX,~N(244,2听o), 其中，(i=1,2,…,n)为常数. 服从正态分布的有限个独立随机变量的线性组合仍服从正态分布 如设X,Y独立，都具有正态分布，则3X+4Y+1也具有正态分布

如设X,Y 独立,都具有正态分布，则 3X+4Y+1也具有正态分布 类似地可以证明: ~ ( , ) 2 2 2  Z  X Y N 1   2  1  若X和Y 独立, 此结论推广到 n个独立的正态随机变量之和的情形 例4(P.89例5) 若X和Y相互独立,且均服从N(0,1), 求Z=X+Y 的密度. 解 f x  e   x ； x X , 2 1 ( ) 2 2  f y  e   y ， y Y , 2 1 ( ) 2 2  由卷积公式    f z  f x f z  x dx Z X Y ( ) ( ) ( ) e e dx x z x        2 2 2 ( ) 2 2 1  e e dx z x z        2 2 ) 2 ( 4 2 1  令 2 z t  x e e dt t z       2 2 4 2 1  . 2 1 4 2 z e    ~ ( , ), ~ ( , ), 2 2 2 2 且 X N  1  1 Y N   请自行写出结论 服从正态分布的有限个独立随机变量的线性组合仍服从正态分布 更一般地, 可以证明: 泊松分布、二项分布 也有相应结论 均匀分布? 其中ai ( i =1,2,…, n)为常数. ~ ( , ), 1 2 2 1 1       n i i i n i i i n i aiXi N a  a  ~ ( , ), 2 i i 若 Xi N   且 X1 , X2 , …, Xn 独立, 则 ∴ Z 服从正态分布N(0,2)

例5若X和Y相互独立，它们分别服从参数为2，的泊松分布， 证明Z=X+Y服从参数为21+2的泊松分布. 解依题意P(X=i)=e2i i=0,1,2,… i! P(r=j)=eu, j=0,1,2,… 由卷积公式P(Z=r)=∑P(X=i)P(Y=r-i), i=0 (r-i)! ea r! 会2君 e-(+五) r! (21+2)',r=0,1,… 即Z服从参数为入+入2的泊松分布

解 依题意  ，       r i P Z r P X i P Y r i 0 ( ) ( ) ( ) 它们分别服从参数为1,2 的泊松分布, 由卷积公式 i = 0, 1, 2, … j =0, 1, 2, … , ! ( ) 1 1 i e P X i i     ， ! ( ) 2 2 j e P Y j j     例5 若X和Y相互独立, 证明 Z=X+Y 服从参数为1 + 2 的泊松分布.        r i i r i r i e i e 0 ! ( )! 1 1 2 2       r i i r i i r i r r e 0 ( ) ! ( )! ! ! 1 2 12   ( ) , ! 1 2 ( 1 2 ) r r e         即 Z 服从参数为 1 + 2 的泊松分布 r = 0, 1, …

例6设X和Y相互独立，X~B(n1,p),Y~B(n2,p),求Z=X+Y的分布. 我们给出不需要计算的另一种证法： 回忆第二章对服从二项分布的随机变量所作的直观解释： 若X~B(n,p),则X是在n,次独立重复试验中事件A出现的次 数，每次试验中A出现的概率都为P. 同样，Y是在，次独立重复试验中事件A出现的次数，每次试 验中A出现的概率为p. 故Z=X+Y是在n,+n,次独立重复试验中事件A出现的次数， 每次试验中A出现的概率仍为p,于是Z是以(n+n2,p)为参数 的二项随机变量，即Z~B(n+n2,p)

例6 设X和Y相互独立, X~B(n1 , p), Y~B(n2 , p),求Z=X+Y 的分布. 回忆第二章对服从二项分布的随机变量所作的直观解释: 我们给出不需要计算的另一种证法: 同样，Y 是在n2次独立重复试验中事件A出现的次数, 每次试 验中A出现的概率为 p. 若 X~ B(n1 , p),则 X 是在 n1次独立重复试验中事件A出现的次 数, 每次试验中A出现的概率都为 p. 故Z=X+Y 是在n1+n2 次独立重复试验中事件A出现的次数, 每次试验中A出现的概率仍为 p，于是Z 是以(n1+n2 , p)为参数 的二项随机变量，即 Z ~ B(n1+n2 , p)