上海交通大学：《概率论与数理统计》课程教学资源（电子讲义）第5章 数理统计的基本概念

第5章 数理统计的基本概念 数理统计是运用概率论的知识，研究如何有效地对带有随机性影响的数据进行收集、 整理、分析和推断的学科，由于随机性现象广泛存在于工、农业生产、工程技术、自然 科学和社会科学等领域中，因此数理统计有着最广泛的应用。 5.1基本概念 1.总体和样本 在数理统计中，我们将研究对象的全体称为总体或母体，而把组成总体的每个元素 称为个体。例如研究一批灯泡的平均寿命时，该批灯泡的全体构成了研究的总体，其中 每个灯泡就是个体。 在实际问题中，研究对象往往是很具体的事物或现象，而我们所关心的不是每一个 个体的种种具体的特征，而是其中某项或某几项数量指标，记为X。在上例中，X即 指该批灯泡的寿命。对不同的个体，X的取值一般是不同的。例如在试验中观察若干个 个体就会得到X的一种数值但在试验或观察之前，无法确定会得到一组什么样的数值， 所以'是一个随机变量或随机向量，而X的分布也就完全描述了我们所关心的指标， 即总体的分布。为方便起见，以后我们将'的可能取值的全体组成的集合称为总体，或 直接称”为总体，的分布也就是总体的分布。 总体分布一般是全部或部分未知的，为了研究总体”的分布规律，我们需要对总体 进行若干次观察。由观察得到总体指标r的一组数值(：，，2，，x,),其中x,为第1次观 察结果，并称(x,x,…,x)为总体r的一组容量为n的样本观察值，样本观察值是对总 体分布进行分析、推断的基础。这种从总体中随机地抽出若干个个体进行观察或实验， 称为随机抽样观察，从总体中抽出的若干个个体称为样本，一般记为(X,X,…,) 而一次具体的观察结果(：，2，，x,)是完全确定的一组数值，但它又随着每次抽样观察 而改变。因此，容量为n的样本(，巧，，n)是n维随机向量，而具体的观察值(，5，， x)是随机变量（X,五，，X)的一个样本观察值。样本（X,五，，)所有可能取 值的全体称为样本空间，记为心，而样本观察值(x,,,)是八中的一个样本点。 随机抽样的目的是为了对总体X的分布进行各种分析推断，所以要求抽取的样本能 很好地反映总体的特性，为此我们要求随机抽取的样本(X,,,X)满足： (1)具有代表性。即样本的每个分量X与X有相同的分布； (2)具有独立性。即X,2,,X是相互独立的随机变量，也就是说，n次观察值 之间是互相独立的： 满足上述两条的样本称为简单随机样本，今后如无特别说明，所说的样本均指简单

第 第 5 5 章 章 数理统计的基本概念 数理统计的基本概念 数理统计的基本概念 数理统计的基本概念 数理统计是运用概率论的知识，研究如何有效地对带有随机性影响的数据进行收集、 整理、分析和推断的学科，由于随机性现象广泛存在于工、农业生产、工程技术、自然 科学和社会科学等领域中，因此数理统计有着最广泛的应用。 5.1 5.1 基本概念 基本概念 1. 1. 总体和样本 在数理统计中，我们将研究对象的全体称为总体或母体，而把组成总体的每个元素 称为个体。例如研究一批灯泡的平均寿命时，该批灯泡的全体构成了研究的总体，其中 每个灯泡就是个体。 在实际问题中，研究对象往往是很具体的事物或现象，而我们所关心的不是每一个 个体的种种具体的特征，而是其中某项或某几项数量指标，记为 X 。在上例中， X 即 指该批灯泡的寿命。对不同的个体，X 的取值一般是不同的。例如在试验中观察若干个 个体就会得到 X 的一种数值但在试验或观察之前，无法确定会得到一组什么样的数值， 所以 X 是一个随机变量或随机向量，而 X 的分布也就完全描述了我们所关心的指标， 即总体的分布。为方便起见，以后我们将 X 的可能取值的全体组成的集合称为总体，或 直接称 X 为总体， X 的分布也就是总体的分布。 总体分布一般是全部或部分未知的，为了研究总体 X 的分布规律，我们需要对总体 进行若干次观察。由观察得到总体指标 X 的一组数值( x 1 , x 2 ,, x n ) ，其中 x i为第i 次观 察结果，并称( x 1 , x 2 ,, x n ) 为总体 X 的一组容量为 n 的样本观察值，样本观察值是对总 体分布进行分析、推断的基础。这种从总体中随机地抽出若干个个体进行观察或实验， 称为随机抽样观察，从总体中抽出的若干个个体称为样本，一般记为 (X1 , X 2 ,, X n ) ， 而一次具体的观察结果( x 1 , x 2 ,, x n ) 是完全确定的一组数值，但它又随着每次抽样观察 而改变。因此，容量为 n 的样本（X1, X2, …, Xn）是 n 维随机向量，而具体的观察值（ x1, x2, …, xn）是随机变量（X1, X2, …, Xn）的一个样本观察值。样本（X1, X2, …, Xn）所有可能取 值的全体称为样本空间，记为，而样本观察值（x 1, x2, …, xn）是中的一个样本点。 随机抽样的目的是为了对总体 X 的分布进行各种分析推断，所以要求抽取的样本能 很好地反映总体的特性，为此我们要求随机抽取的样本（X1, X2, …, Xn）满足： （1）具有代表性。即样本的每个分量 Xi与 X 有相同的分布； （2）具有独立性。即 X1, X2, …, Xn是相互独立的随机变量，也就是说，n 次观察值 之间是互相独立的； 满足上述两条的样本称为简单随机样本，今后如无特别说明，所说的样本均指简单

随机样本。 例1对一批N件产品情况进行检查，从中有放回的抽取n件。分别以1,0表示 某件产品为合格品和次品，以(0≤日≤1)表示产品的合格路率，则总体指标服从参 数为0的(0-1)分布，即P(=x)=0(1-0)-r,x=0,1。这样抽取得到的观察结果为 ,,,X为一个简单随机样本，也就是说，，，Xn是相互独立且均服从参数为0 的(0-1)分布，故样本（K,,,X)的联合分布律为 AK=x,K2=x,,X。=x)=Πg1-0), n=0,1,=1,2,..no 每组观察值(：，2，，x)为由0,1组成的一个n维向量，其样本空间为 ={（1,,,xn)|x=0,1,=1,2,…}。 共有2”个样本点。 一般地，若总体X的概率密度或联合分布律为八)，则样本(，，，)的联合密 度或联合分布律为 L(x,32x)=八x) 并称L（x,,,xn)为样本(X,,,n)的似然函数。 对于个体为有限的总体来说，采用有放回随机抽样就能得到简单随机样本。但有放 回抽样使用起来很不方便。又由于当总体的个体为无限时，有放回抽样与不放回抽样没 有什么区别，因此，在实际问题中，当总体中个体数N很大，而样本容量相应较小时， 可把总体看作是无限的，从而可将不放回抽样当作有放回抽样来处理。 2.统计量和样本矩 样本是我们进行分析和推断的起点，但实际上我们往往并不直接利用样本进行推 断，而需要对样本进行一番“加工”和“提炼”，将分散于样本中的信息集中起来。为 此我们引进统计量的概念。 设K,,,Xn为来自总体的一个样本，g(,,,n)为一个n元连续函数， 若g(X,,,n)中不含任何未知参数，则称g(X,,,Xn)为一个统计量。显然 统计量也是一个随机变量。以后，针对不同的问题我们总是构造相应的统计量以实现对 总体的统计推断。 例如，设总体r服从正态分布N（4,。2)其中4，。2未知。K,5,,Xn是从

随机样本。 例 1 1 对一批 N 件产品情况进行检查，从中有放回的抽取 n 件。分别以 1，0 表示 某件产品为合格品和次品，以(0    1）表示产品的合格路率，则总体指标 X 服从参 数为 的（0-1）分布，即 P（X = x）= x (1 ) 1x , x  0,1 。这样抽取得到的观察结果为 X1, X2, …, Xn为一个简单随机样本，也就是说 X1, X2, …, Xn是相互独立且均服从参数为θ 的（0-1）分布，故样本（X1, X2, …, Xn）的联合分布律为 i x i ， n i x P X x X x X n x n Q         1 1 1 1 2 2 ( , ,..., ) (1  ) xn = 0，1，i=1，2，…n。 每组观察值（x1, x2, …, xn）为由 0，1 组成的一个 n 维向量，其样本空间为 ={（x1, x2, …, xn）| xi =0，1，i=1，2，…n}。 共有 2 n 个样本点。 一般地，若总体 X 的概率密度或联合分布律为 f (x)，则样本(X1, X2, …, Xn)的联合密 度或联合分布律为 ( , ,..., ) ( ) 1 1 2    n i n i L x x x f x 并称 L（x1, x2, …, xn）为样本（X1, X2, …, Xn）的似然函数。 对于个体为有限的总体来说，采用有放回随机抽样就能得到简单随机样本。但有放 回抽样使用起来很不方便。又由于当总体的个体为无限时，有放回抽样与不放回抽样没 有什么区别，因此，在实际问题中，当总体中个体数 N 很大，而样本容量 n 相应较小时 ， 可把总体看作是无限的，从而可将不放回抽样当作有放回抽样来处理。 2. 2. 统计量和样本矩 统计量和样本矩 统计量和样本矩 统计量和样本矩 样本是我们进行分析和推断的起点，但实际上我们往往并不直接利用样本进行推 断，而需要对样本进行一番“加工”和“提炼”，将分散于样本中的信息集中起来。为 此我们引进统计量的概念。 设 X1, X2, …, Xn为来自总体 X 的一个样本，g（X1, X2, …, Xn）为一个 n 元连续函数， 若 g（X1, X2, …, Xn）中不含任何未知参数，则称 g（X1, X2, …, Xn）为一个统计量。显然 统计量也是一个随机变量。以后，针对不同的问题我们总是构造相应的统计量以实现对 总体的统计推断。 例如，设总体 X 服从正态分布 N（ ， ）其中 ， 未知。X1, X2   2   2 , …, Xn是从

正态总休冲轴取的一个样本，则之，立， 7 均足样本的能。而空-，。 立，畜不是统计量 下面介绍一类常用的统计量—一样本矩。 设（K,5,,X)为一个简单随机样本，则称 A,= n ,r=1,2,… 为一阶样本原点矩，特别地，称4为样本均值，并记为开，即了=∑X, 称 B=2(K-r=2,3) ni= 为，阶样本中心矩。其中的B,称为2阶样本中心矩。但为了今后的需要，我们定义样本 方差如下： 若总体X的期望4=E()和方差o?=D()存在，则 A=时20-2A0=4 n=20-7200-元 s)=A2(K-1=A2P-m1 i) 2+ax胖-五+a 2a+){+r小-o

正态总体 X 中抽取的一个样本，则  ， ,  n i X i n 1 1   n i Xi 1 2 均是样本的统计量，而    ， ，都不是统计量.  n i i x n 1 1   n i i x 1 2 2 1  下面介绍一类常用的统计量——样本矩。 设（X1, X2, …, Xn）为一个简单随机样本，则称 , 1 , 2 , 1 1     X r n A n i r r i 为 r r 阶样本原点矩，特别地，称 A1 为样本均值，并记为 X ，即    n i X i n X 1 1 称 ( ) ( 2,3, ) 1 1       X X r n B r n i r i 为 r r 阶样本中心矩。其中的 B2 称为 2 阶样本中心矩。但为了今后的需要，我们定义样本 方差如下： 2 1 2 ( ) 1 1 X X n S n i i      若总体 X 的期望 = E (X )和方差2 = D ( X )存在，则         ( ) 1 ) 1 ( ) ( 1 1 n i i n i i E X n X n E X E n D X n X n D X D n i i n i i 2 1 2 1 ( ) 1 ) 1 ( ) (         [ ] 1 1 [ ( ) ] 1 1 ( ) 2 1 2 2 1 2 E X nX n E X X n E S n i i n i i           ( ) 1 1 ( ) 1 1 2 2 1 E X n E X n n i i       { ( ) [ ( )] } 1 1 { ( ) [ ( )] } 1 1 2 2 1 D X E X n D X E X n i n i i         2 2 2 2 1 2 1 ( ) 1 1                       n n n n n i

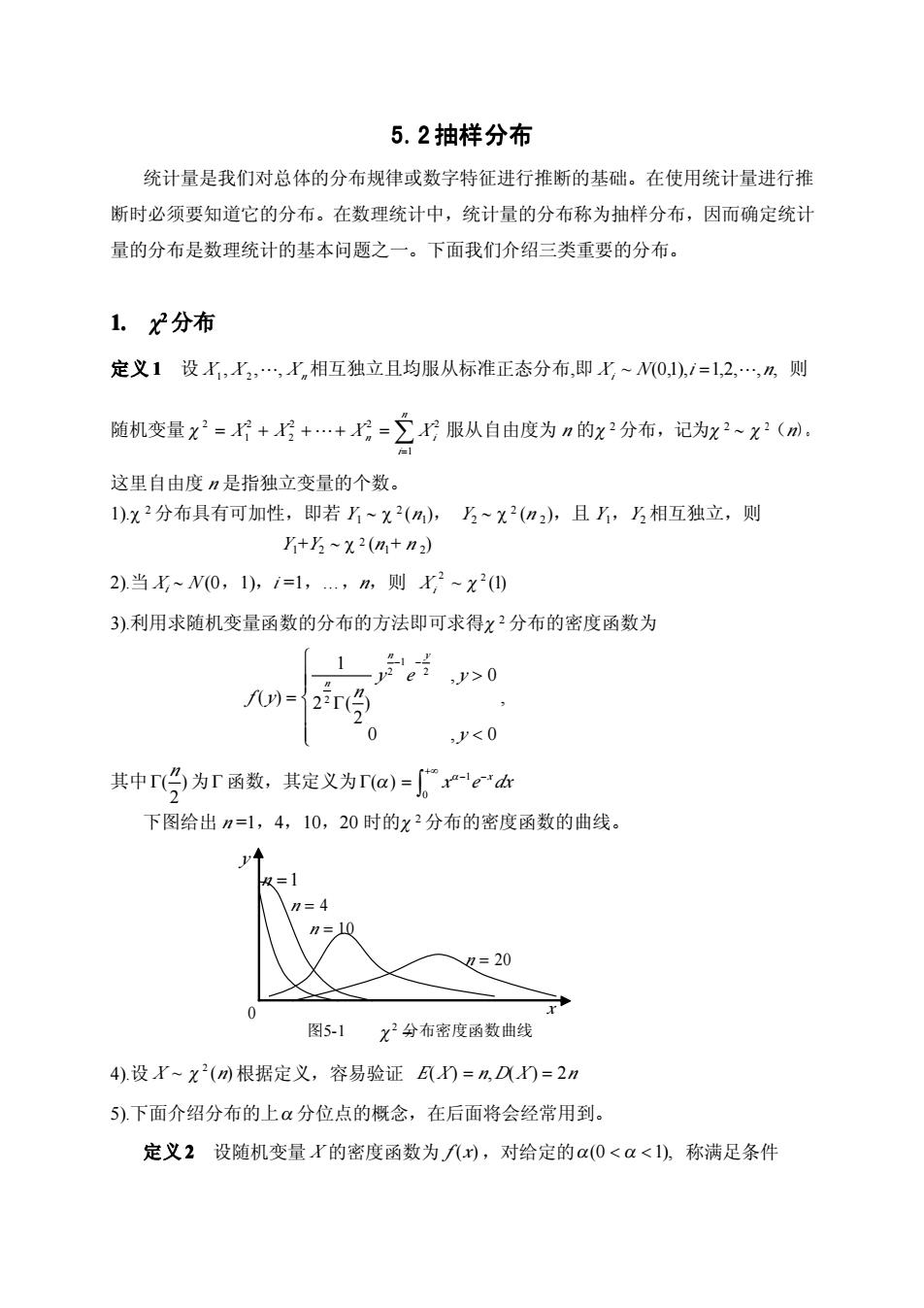
5.2抽样分布 统计量是我们对总体的分布规律或数字特征进行推断的基础。在使用统计量进行推 断时必须要知道它的分布。在数理统计中，统计量的分布称为抽样分布，因而确定统计 量的分布是数理统计的基本问题之一。下面我们介绍三类重要的分布。 1.x分布 定义1设K,X2,,Xn相互独立且均服从标准正态分布，即X,~N0,1),1=1,2,,2,则 随机变量x2=+++松=2服从自由度为n的x2分布，记为x2~x2(m。 这里自由度n是指独立变量的个数。 1)x2分布具有可加性，即若乃~x2(,乃~x2(n2),且，乃相互独立，则 +~X2(h+n2) 2).当~N(0,1),i=1,.,n,则X2~X2(①) 3)利用求随机变量函数的分布的方法即可求得×2分布的密度函数为 1-y2e2 2-1-2 ,y>0 f)= 2r 0 ,y<0 其中r台为r函数，其定义为ra)=-ek 下图给出n=1,4,10,20时的x2分布的密度函数的曲线。 n=10 n=20 图5-1X2分布密度函数曲线 4).设X~x2()根据定义，容易验证E()=n,D()=2n 5).下面介绍分布的上α分位点的概念，在后面将会经常用到。 定义2设随机变量r的密度函数为f(x),对给定的a(0<a<1),称满足条件

5.2 5.2 抽样分布 抽样分布 统计量是我们对总体的分布规律或数字特征进行推断的基础。在使用统计量进行推 断时必须要知道它的分布。在数理统计中，统计量的分布称为抽样分布，因而确定统计 量的分布是数理统计的基本问题之一。下面我们介绍三类重要的分布。 1. 1.   2 2 分布 定义 1 1 设 X1 , X 2 ,, X n相互独立且均服从标准正态分布,即 Xi ~ N(0,1),i 1,2,,n, 则 随机变量 服从自由度为 n 的 2 分布，记为 2    2（n）。       n i X X X n X i 1 2 2 2 2 2 1  2  这里自由度 n 是指独立变量的个数。 1). 2 分布具有可加性，即若 Y1   2 (n1)， Y2   2 (n 2)，且 Y1，Y2 相互独立，则 Y1+Y2   2 (n1+ n 2) 2).当 Xi  N (0，1)，i =1，…，n，则 ~ (1) 2 2 Xi  3).利用求随机变量函数的分布的方法即可求得 2 分布的密度函数为 ,              0 , 0 , 0 ) 2 2 ( 1 ( ) 2 1 2 2 y y e y n f y n y n 其中 ) 为 函数，其定义为 2 ( n   x e dx x      0 1 ( )   下图给出 n =1，4，10，20 时的 2 分布的密度函数的曲线。 4).设 X ~  2 (n) 根据定义，容易验证 E(X)  n,D(X )  2n 5).下面介绍分布的上 分位点的概念，在后面将会经常用到。 定义 2 2 设随机变量 X 的密度函数为 f (x) ，对给定的(0    1), 称满足条件 y 0 x n  1 n  4 n  10 n  20 图5-1 分布密度函数曲线  2 

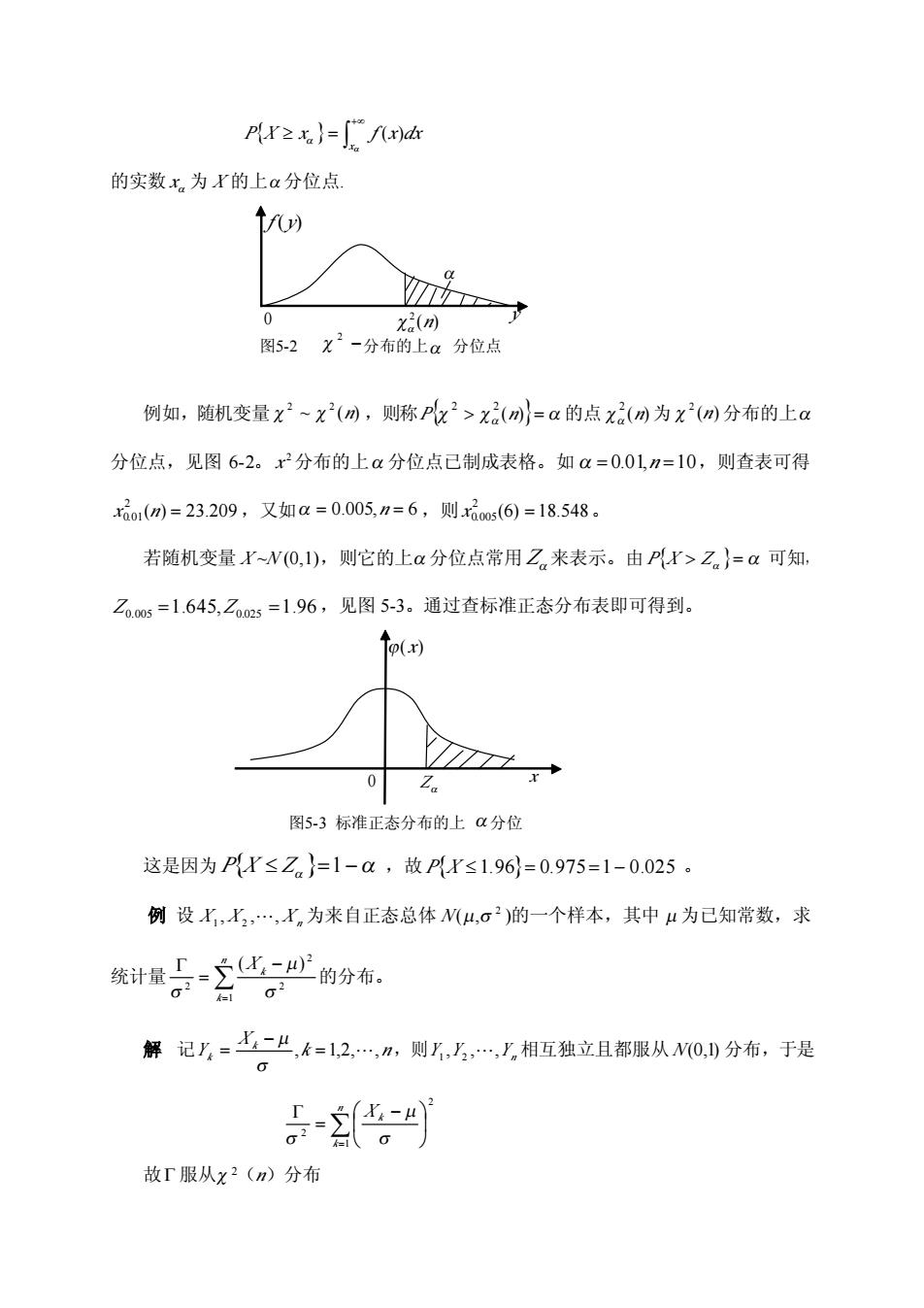
PK≥xa}=e 的实数x为r的上a分位点 f) X.() 图5-2x2-分布的上a分位点 例如，随机变量x2~x(m,则称Pz2>x2(m}=a的点x2(m为x2(m分布的上a 分位点，见图6-2。x2分布的上分位点已制成表格。如a=0.01=10,则查表可得 x1(m)=23.209,又如a=0.005,n=6,则xos(6)=18.548。 若随机变量X~W(0,1),则它的上a分位点常用Z来表示。由P{r>Z}=a可知， Z.os=1.645,Z2s=1.96,见图5-3。通过查标准正态分布表即可得到。 o(x) 0 图5-3标准正态分布的上分位 这是因为Pr≤Z}=1-a，故Pr≤1.96}=0.975=1-0.025。 例设X,X2,,n为来自正态总体N(4,o2)的一个样本，其中4为已知常数，求 统计量。-三华，心的分布。 σ2 解记y=七-严，k=12,,m,则，，，y相互独立且都服从N0,分布，于是 G -。 故T服从x2(n)分布

        x P X x f (x)dx 的实数 为 的上 分位点.  x X  例如，随机变量  2 ~  2 (n) ，则称P 2    2 (n)   的点   2 (n) 为  2 (n) 分布的上 分位点，见图 6-2。 x 2分布的上 分位点已制成表格。如   0.01,n 10，则查表可得 x 0 2 .01(n)  23.209 ，又如  0.005,n  6 ，则 x 0 2 .005(6)  18.548。 若随机变量 X ~N (0,1)，则它的上 分位点常用 Z来表示。由 PX  Z     可知， Z 0.005 1.645,Z 0.025 1.96，见图 5-3。通过查标准正态分布表即可得到。 这是因为 PX  Z 1  ，故 PX  1.96 0.975 1  0.025 。 例 设 X1 , X 2 ,, X n为来自正态总体 N(, 2 )的一个样本，其中  为已知常数，求 统计量  的分布。     n k k X 1 2 2 2 ( )    解 记 k n，则 相互独立且都服从 分布，于是 X Y k k ,  1,2,,     Y Y Yn , , , 1 2  N(0,1) 2 1 2            n k X k    故 服从  2（n）分布 0  ( ) 2  n f (y) y 图5-2 分布的上 分位点 2   0 x ( x) Z  图5-3 标准正态分布的上 分位 点 

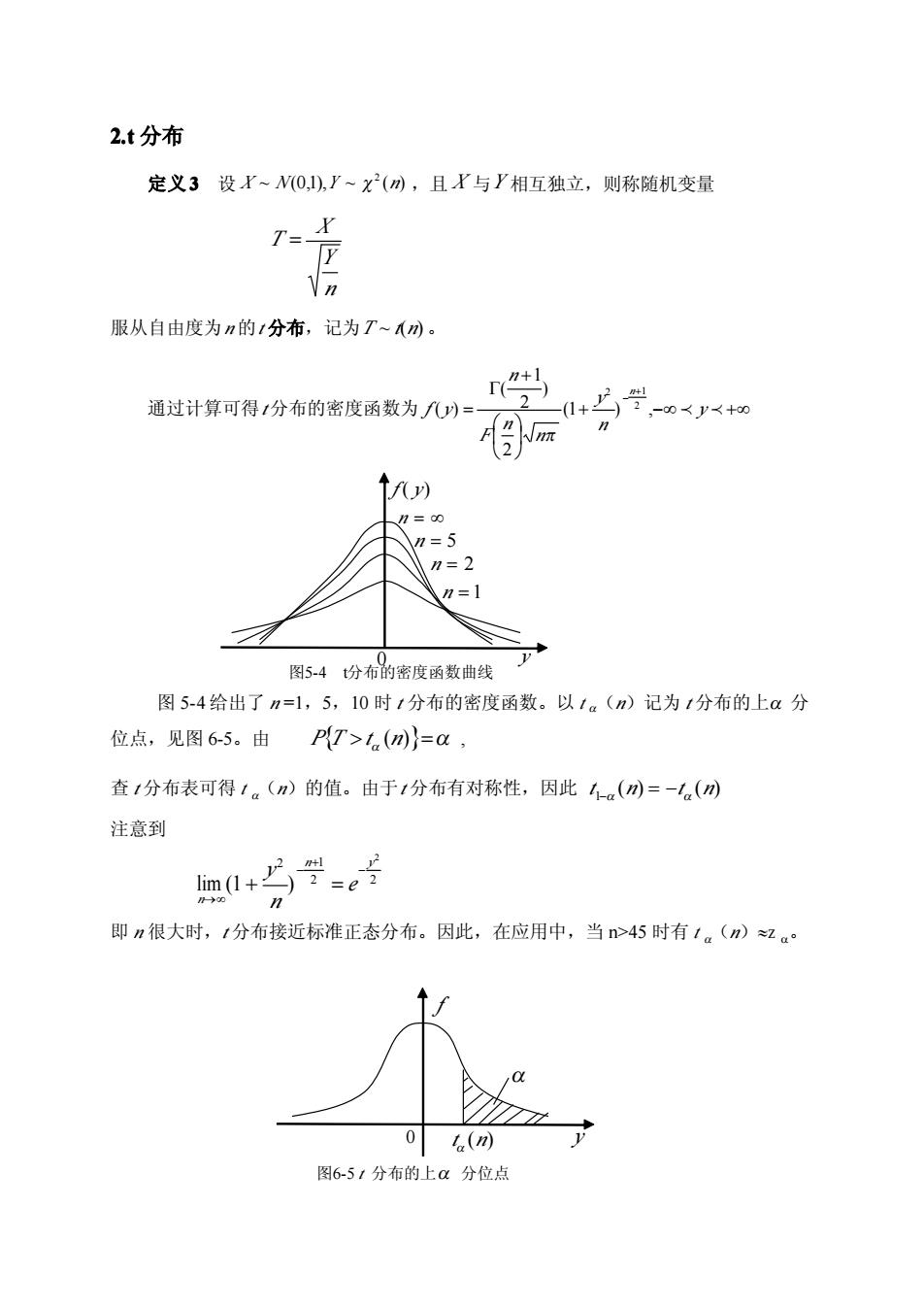
2.t分布 定义3设r~W(0,1),'~x(m,且X与厂相互独立，则称随机变量 T= 服从自由度为n的1分布，记为T~(m。 1 通过计算可得1分布的密度函数为八)= 1+岁-mt(n)=a, 查1分布表可得1。(n)的值。由于1分布有对称性，因此4a()=-a() 注意到 m+上罗=e 几→0 即n很大时，1分布接近标准正态分布。因此，在应用中，当n>45时有1。(n)z。° 0(m） 图6-51分布的上a分位点

2.t 2.t 分布 定义 3 3 设 X ~ N(0,1),Y ~  2 (n) ，且 X 与Y 相互独立，则称随机变量 n Y X T  服从自由度为n 的t 分布，记为T ~ t(n) 。 通过计算可得t分布的密度函数为                y  n y n n F n f y n (1 ) , 2 ) 2 1 ( ( ) 2 2 1  图 5-4 给出了 n =1，5，10 时 t 分布的密度函数。以 t （n）记为 t 分布的上 分 位点，见图 6-5。由    , P T t  (n)  查 t 分布表可得 t （n）的值。由于t 分布有对称性，因此 ( ) ( ) 1 t n t n      注意到 2 2 2 1 2 lim (1 ) n y n e n y       即 n 很大时，t 分布接近标准正态分布。因此，在应用中，当 n>45 时有 t （n）z 。 f ( y) 0 y n   n  5 n  2 n  1 图5-4 t分布的密度函数曲线 0 图6-5 t 分布的上 分位点 f  t (n)  y

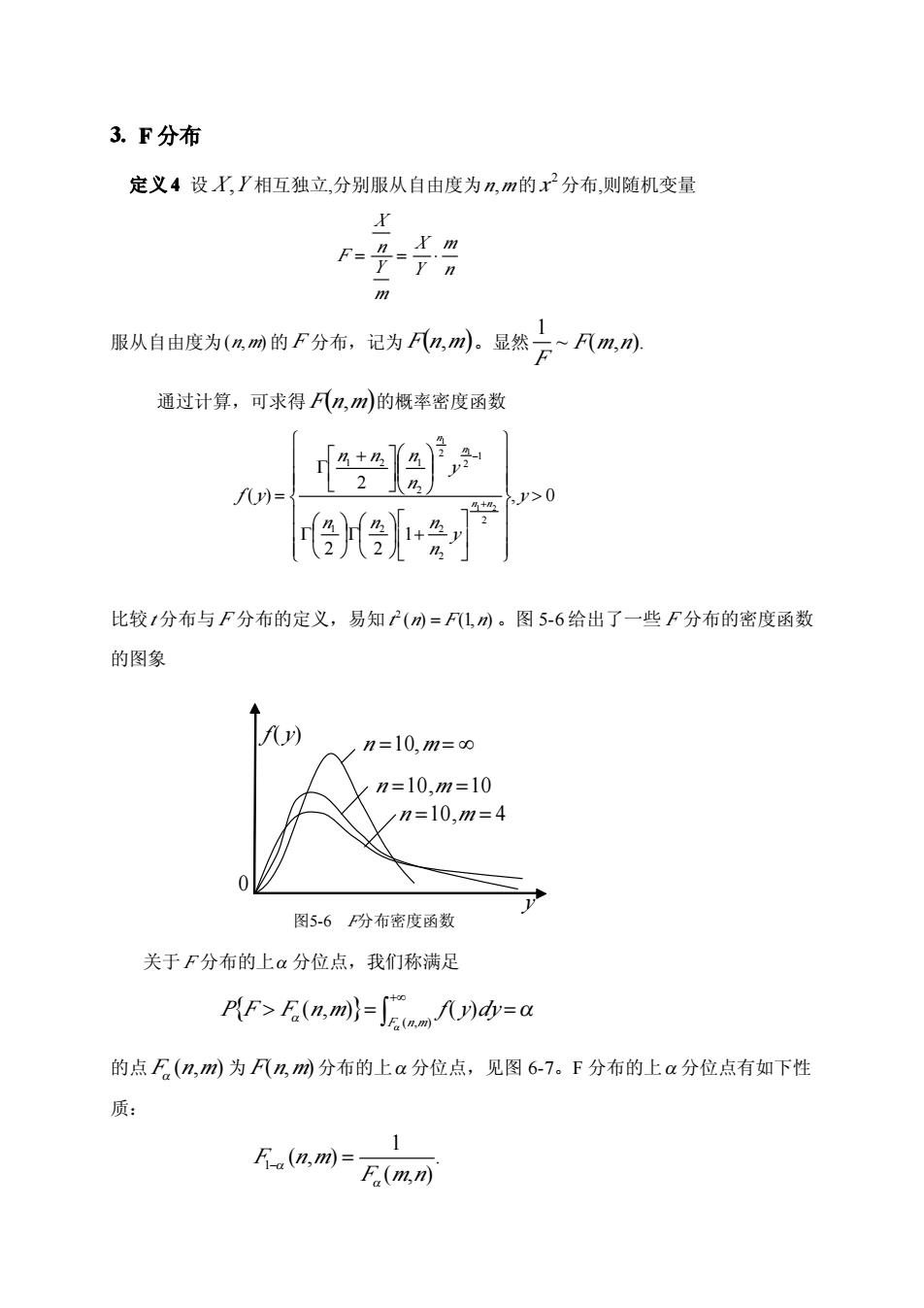
3.F分布 定义4设X,'相互独立，分别服从自由度为n,m的x分布，则随机变量 X F=I X m m 服从自由度为（以m的F分布，记为心，川。显然二凡m) 通过计算，可求得Fn,m的概率密度函数 f)= y>0 比较1分布与F分布的定义，易知(m=F1,m。图5-6给出了一些F分布的密度函数 的图象 n=10,m=o n=10,m=10 n=10,m=4 图5-6F分布密度函数 关于F分布的上α分位点，我们称满足 PF>F(nm)=dy=a 的点F(n,m)为Fn,网分布的上a分位点，见图6-7。F分布的上a分位点有如下性 质： fa(n,m）=- F(mn)

3. 3. F F 分布 定义 4 4 设 X,Y 相互独立,分别服从自由度为n,m的 x 2分布,则随机变量 n m Y X m Y n X F    服从自由度为(n,m) 的 F 分布，记为 Fn,m。显然 ~ ( , ). 1 F m n F 通过计算，可求得 Fn,m的概率密度函数 , 0 1 2 2 2 ( ) 2 2 1 2 2 1 2 2 2 1 2 1 1 2 1 1                                                           y y n n n n y n n n n f y n n n n 比较t 分布与 F 分布的定义，易知 t 2 (n)  F(1,n) 。图 5-6 给出了一些 F 分布的密度函数 的图象 关于 F 分布的上 分位点，我们称满足           ( , ) ( , ) ( ) F n m P F F n m f y dy 的点 F (n,m) 为 F(n,m) 分布的上 分位点，见图 6-7。F 分布的上 分位点有如下性 质： . ( , ) 1 ( , ) 1 F m n F n m    f ( y) 0 y 图5-6 F分布密度函数 n 10,m   n 10,m 10 n 10,m  4

事实上，设F~F(n,m,则 m 且 a=ra=A作同 1-1-d f(r) F (n,m) 图6-7F分布的上0分布点 于是 1 =1-0, F(n,m) 由a分位点的定义，显然F.(m,)=1 一成立。 F (n,m) 理论上，若总体的分布己知，统计量的分布总是确定的。但对一般的总体分布，统 计量的分布计算往往很复杂，甚至不能求出。这里我们考虑正态总体分布的抽样分布。 一方面是因为其抽样分布较容易求出，另一方面是正态分布可以作为很多统计问题中总 体分布的近似。 定理1设X,X,,广，是从正态总体W(u,o)中抽取的一个简单随机样本，F 与S2分别为样本均值和样本方差，则 ①F-Au 2)-)2 g°r产(n-1

事实上，设 F ~ F(n,m) ，则 ~ ( , ), 1 F n m F 且   , ( , ) 1 1 1 ( , ) 1 1 1 ( , ) 1 1 ( , )                             F F n m P F F n m P F F n m P F F n m P      于是  ,           1 ( , ) 1 1 F F n m P 由分位点的定义，显然 成立。 ( , ) 1 ( , ) 1 F n m F m n    理论上，若总体的分布已知，统计量的分布总是确定的。但对一般的总体分布，统 计量的分布计算往往很复杂，甚至不能求出。这里我们考虑正态总体分布的抽样分布。 一方面是因为其抽样分布较容易求出，另一方面是正态分布可以作为很多统计问题中总 体分布的近似。 定理 1 1 设 X1 , X 2 ....,X n 是从正态总体 N(,2 ) 中抽取的一个简单随机样本，X 与 S 2分别为样本均值和样本方差，则 (1) ~ ( , ); 2 n X N   (2) ~ ( 1); ( 1) 2 2 2   x n n S  f ( y ) 0 y  F (n,m)  图6-7 F分布的上  分布点

(3)Y与S2相互独立。（证明略） 推论1 T= X-4~n-1) n 证由定理知 T-L、N(0,1.a-1)5、xa-1) 02 √n 且二者相互独立，由定义6.3可知 X-μ w-1)s_X-L-n-1) 2(n-1) 即T~(n-1) 设X,K2,Xn与，，厂n分别为来自正态总体W(41,012)和W(41,022)的简 单随机样本，且两样本之间相互独立，若 2-万.s2-升 n-1 则 0F=S三-lm-以 2 S2o17 (2)若进一步假设o2=022，有 7-F-7-4=)、+m-2） 1,1 一十一 其中 S2=w-l10S2+m-1g2 ∑（出-+2U- n+m-2 n+m-2 以上结论在后面将经常用到，必须记住。另外，对其它总体，虽然很难求到其精确 的抽样分布，但我们可以利用中心极限定理等理论得到当较大时的近似分布，这就是

(3) X 与 相互独立。(证明略) 2 S 推论 推论 1 1 ~ ( 1).   t n n S X T  证 由定理知   ~  1  1 ~ ( 0 ,1), 2 2 2    x n n S N n X    且二者相互独立,由定义 6.3 可知   ~ ( 1) ( 1) 1 2 2       t n n S X n n S n X     即T ~ (n 1) 设 X 1 , X 2 ....,X n与Y1 ,Y2 ....,Ym分别为来自正态总体 ( , ) 和 的简 2 N 1  1 ( , ) 2 N 1  2 单随机样本，且两样本之间相互独立，若             m i i n i i Y Y m X X S n S 1 2 2 2 1 2 2 1 1 1 ( ) , 1 1 则 (1) ~ ( 1, 1); 2 1 2 2 2 2 2 1   F n  m  S S F   (2) 若进一步假设 ，有 2 2 2 1  ~ ( 2) 1 1 ( ) 1 2        t n m n m S X Y T w   其中 2 2 2 2 2 1 2 1 1 ( ) ( ) ( 1) ( 1) 2 2 n m i i i i w X X Y Y n S m S S n m n m                 以上结论在后面将经常用到，必须记住。另外，对其它总体，虽然很难求到其精确 的抽样分布，但我们可以利用中心极限定理等理论得到当 n 较大时的近似分布，这就是

统计问题中的大样本问题，在此我们不加讨论。 例从正态总体W(4,o2)中抽取容量为16的样本，试求： (1)已知o2=25:(2)o2为知，但已知样本方差52=20.8的情况下，样本均值x与 总体均值4之差的绝对值小于2的概率。 解(1)由于统计量 4=-L、N(0,1 n 因此在o2已知时， =P\4<1.6=(1.6)-(-1.6)=2(1.6)-1=2×0.9452-1=0.8904 (2)由于σ2未知，但5S2=20.8,这时统计量 1=-4n-10, S n 因此 -小以7而 =P<1.754}=1-P1≥1.754} 查1分布表得10.05(16-1)=1.753，P(1≥1.753)=0.05。由此可得 P行-4<2}1-2×0.05=0.90 例设总体r服分布N(72,100),为使样本均值大于70的概率不小于90%，则样 本容量应取多少？ 解设所需样本容量为，由于 x-'n~N0,)

统计问题中的大样本问题，在此我们不加讨论。 例 从正态总体 N(,2 ) 中抽取容量为 16 的样本，试求： (1) 已知2  25；(2) 2为知，但已知样本方差 S 2  20.8 的情况下，样本均值 x 与 总体均值  之差的绝对值小于 2 的概率。 解 (1) 由于统计量 ~ N ( 0 ,1), n x      因此在2 已知时，    1.6 (1.6) ( 1.6) 2 (1.6) 1 2 0.9452 1 0.8904; 5 2 4 4 5 2 2                                                       P u x P n n x P x P (2) 由于2 未知，但 S 2=20.8，这时统计量 ~ ( 1),   t n n S x t  因此    1 .754  1  1 .754  4 .56 16 2 2 2                                  P t P t S n x P S n S n x P x P    查 t 分布表得 t 0.05(16-1)=1.753，P (t 1.753)=0.05。由此可得 P x    2  1  2  0 . 05  0 .90 例 设总体 X 服分布 N (72，100)，为使样本均值大于 70 的概率不小于 90%，则样 本容量应取多少? 解 设所需样本容量为 n，由于 n ~ N(0,1) , x   