上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）07、多维随机变量及分布 §3.1 二维随机变量 §3.2 边缘分布

第三章 多维随机变量 及其分布

第三章 多维随机变量 及其分布

身高Y 很多随机现象需要用多个随机变量来描述， 飞机的重心在空中的位置是由 三个随机变量（三个坐标）来确定的. 检察某大学的全体学生的身体状况，从其中随机抽取 一个学生，分别以X和Y表示其体重和身高. 体重X 完全类似于上章中对一维随机变量的研究，我们将研究 多维随机变量及其分布.它是上一章内容的推广. 类比 多维随机变量 作为一个整体的分布 平行于一维的结论 转化 特有内容：变量之间的边缘分布、条件分布、 独立性等 类似多元函数微积分，从二维推广到多维 无实质性的困难，我们重点讨论二维随机变量

从其中随机抽取 一个学生，分别以X 和Y 表示其体重和身高. 体重X 身高Y 很多随机现象需要用多个随机变量来描述. 飞机的重心在空中的位置是由 三个随机变量(三个坐标)来确定的. 类似多元函数微积分, 从二维推广到多维 无实质性的困难，我们重点讨论二维随机变量 . 完全类似于上章中对一维随机变量的研究, 我们将研究 多维随机变量及其分布. 多维随机变量 作为一个整体的分布 平行于一维的结论 特有内容: 变量之间的边缘分布、条件分布、独立性等 检察某大学的全体学生的身体状况, 类比 转化 它是上一章内容的推广

§3.1二维随机变量 一、 二维随机变量及其分布函数 注意与一维情形 1.二维随机变量 的类比与对照 定义我们称个定义在同一个样本空间上的随机变量的整体 X=(X,X2,.,Xm)为n维随机变量或n维随机向量 以下只讨论二维随机变量（X,Y). 类似于一维随机变量可视为直线（一维空间）上的随机点，二维 随机变量可视为平面上（二维空间）的随机点 下面研究的思路与一维一致一使用分布函数， 概率分布和 概率密度等函数，来刻划作为一个整体的二维随机变量的统计规律

定义 我们称 n 个定义在同一个样本空间上的随机变量的整体 X=(X1, X2 , …，Xn )为n维随机变量 或 n维随机向量. §3.1 二维随机变量 注意与一维情形 的类比与对照 一、二维随机变量及其分布函数 • 类似于一维随机变量可视为直线(一维空间)上的随机点,二维 随机变量可视为平面上(二维空间)的随机点 . • 下面研究的思路与一维一致 —— 使用分布函数, 概率分布和 概率密度等函数,来刻划作为一个整体的二维随机变量的统计规律. 1. 二维随机变量 以下只讨论二维随机变量 (X, Y )

2.二维随机变量的分布函数 定义1(P.63定义2)设(X,)是二维随机变量，V,y∈R,二元函数 F(x) AP(X≤x) 称为二维随机变量(X,Y)的分布函数，也称为随机变量X与Y的 联合分布. y 几何解释 FK,)表示随机点X,Y)落在 以（化，y)为顶点，且位于该点左下方的无穷矩形 内的概率 七 2 P(x1<X≤X2} =F(x2) -F(x1) ✉

也称为随机变量X与Y的 联合分布. 以(x,y )为顶点,且位于该点左下方的无穷矩形 y x o (x, y) .  P(X  x, Y  y)  二元函数 F(x, y)  P{(X  x)(Y  y)}  P(X  x2 ;Y  y2 ) 2. 二维随机变量的分布函数 定义1(P.63 定义2) 设(X, Y)是二维随机变量, x, yR, 称为二维随机变量(X,Y )的分布函数， ) ) ( , ) ( , 1 ) ( 1 , 1 ) ( 1 , 2 ) 2 2 2  F x y  F x y  F x y  F x y  P(X x1 ;Y  y2 ) ( ; )  P X  x2 Y  y1  P(X  x1 ;Y  y1 ) 几何解释 F(x, y) 表示随机点(X ,Y )落在 内的概率. y x o y2 y1 x1 x2 ( , ) ( , ) ( , ) ( , )  F x2 y2  F x2 y1  F x1 y1  F x1 y2 P( x1  X  x2 } ; y1Y  y2 )

3.二维随机变量分布函数的特征性质 10 (单调不减性)F(x,y)分别关，y是单调不减的 20 (极限性质)0≤F飞，y)≤1，且F(-9,-o四=0，F+∞+∞=1； x,F(x,=四=0，y,F(-9y)=0. 30 (右连续性)F(x+0,y)=F(x,y),F(x,y+0)=F(x,y): 40H1<x2,1<y2,F(x2,y2)+Fx1,y)-F(x2,y)-Fx1,y2≥0. y (x,y) Yxyz (x2,y2) (x1,V1) (2,1) 0 X 对对X ✉

即,对任意固定的 y,F( x, y ) 是单调不减函数 对任意固定的 x,F( x, y ) 是单调不减函数, F(x, y) 且F( , ) 3. 二维随机变量分布函数的特征性质 2 0 (极限性质) 3 0 (右连续性) 1 0 (单调不减性) F(x, y)分别关于x, y是单调不减的. 0 1, F(x0, y)  F(x, y), F(x, y0)  F(x, y); 4 0 , 1 2 ,  x1 x2 y  y y x o (x, y) x x x P{ x1  X  x2 ; y1 Y  y2 }  0 lim F(x, y)  1; y x    0, x, F(x, ) 0, y, F( , y)  0. F( ,  ) y x o ( , ) ( , ) ( , 1 ) ( 1 , 2 ) 0. F x2 y2  F x1 y1  F x2 y  F x y  ( , ) x1 y2 ( , ) x2 y2 ( , ) x2 y1 . . . . ( , ) x1 y1

例1(P.64例1)设(X,Y)的联合分布函数是 F比，2AB+arctan)(C+arctan, x,y∈R 其中A,B,C为常数， (I)确定A,B,C的值； (2)求P(2<X<+o,0<Y≤3). 解(1)由分布函数的基本性质知 Fto,o)=A(B+2)(C+)=L,→A≠0，B+受0，C+受*0， Fm+四=A(B-2)C+=0 四=A(B+(C-药)=0户B-号=0， →B=C=受，A=克.F(x,)=之（号+arctan吃）（爱+aretan3, x,y∈R (2)P(2<X<+∞，0<Y≤3)=F(+∞3)-F(+∞0)-F(2,3)+F(2,0) 京受+)受+翠)-（受+）（受+0） 京（受+孕受+军）+之空+军（受+0

P(2 X , 0Y 3)  F( , 3)F( , 0)F(2, 3) F(2, 0) 解 ⑴ ⑴ 确定A ,B ,C 的值; ⑵ 求 P(2<X<+, 0<Y 3). 例1(P.64 例1) 设(X,Y )的联合分布函数是 其中 A ,B ,C 为常数 , x y R y C x F x y  A B  ), ,  3 )( arctan 2 ( , ) ( arctan F(, )  1 ) 1, 2 )( 2  (      A B C ) 0, 2 )( 2 ( ,  )  (      F A B C ) 0, 2 )( 2 ( ,  )  (      F A B C ⑵ ) 2 4 )( 2 2 ( 1 2         0, 2 0, 2   0,       A B C . 1 , 2 2   B C  A 0, 2 0, 2           B C 0) 2 )( 2 2 ( 1  2       ) 2 4 )( 2 4 ( 1 2         0) 2 )( 2 4 ( 1  2       由分布函数的基本性质知 x y R x y F x y    ), ,  3 arctan 2 )( 2 arctan 2 ( 1 ( , ) 2    . 16 1 

二、二维离散型随机变量及其分布列 二维离散型随机变量 类比 维离散型随机变量 (X,Y)=(x,yj),i,j=1,2, X=x)j=1,2,… P.65定义3 (X,Y)的概率分布 X的概率分布 P(X=xi,Y=yj)=Pij 分布列 X和Y的 P(X=xj)=Pi 非负性 P≥0， 联合分布列 乃≥0； 规范性 ΣΣ，=1 可表示为 表格形式 E1. X和Y的联合分布函数 X的分布函数 F(x,y)=PX≤x,Y≤y) F(x)=P(X≤x) =∑∑Pi(-0<x,y<0) P1 xi≤x xi≤xy≤y

二、 二维离散型随机变量及其分布列 二维离散型随机变量 (X,Y)(xi , y j ), i, j 1,2,  (X,Y )的概率分布 一维离散型随机变量 X xj , j 1, 2,         1. 0; j j j p p X 的概率分布 P X xj pj ( ) 分布列 ( , ) P Xxi Y yj X 和Y 的 联合分布列        1 0, i j ij ij p p 可表示为 表格形式 X 的分布函数      x x j j p F(x) P(X x) X 和Y 的联合分布函数 F(x, y)  P(X x, Y  y) (  x, y ) 类比        1 0, i j ij ij p 非负性 p 规范性 P.65 定义3 pij      y y ij xi x j p

例2设随机变量X在1,2,3,4中等可能地取值， Y在1一X中等可能地取整数值，求(X,Y)的分布列. 解确定随机变量的取值 F(x,y)=P(X≤x,Y≤y) Pii =P(X=i,Y=j) =∑P =P({X=i}∩{Y=j) xi≤x,y防≤y F(2,2)=P(X≤2，Y≤2) =P(Y=jX=i)·P(X-n =∑p =4 P.67例3请自读 xi≤2，yj≤2 (i=1,2,3,4,j≤i) =P(X=1,Y=1) 2 3 4 +P(X=1,Y=2) 1/4 1/8 1/12 1/16 +P(X=2,Y=1) 2 0 1/8 1/12 1/16 +P(X=2,Y=2) 3 0 1/12 1/16 =1/2 0 0 0 1/16

{Xi , Y j} {Xi}{Y j}  P(Yj X i)P(Xi) ij p  P({Xi}{Y j }) 例2 设随机变量 X在 1,2,3,4 中等可能地取值, Y 在 1—X 中等可能地取整数值, 求( X,Y)的分布列. 解 确定随机变量的取值 ( 2, 2) ( 2, 1) ( 1, 2 ) ( 1, 1)             P X Y P X Y P X Y P X Y ( i1, 2, 3,4, j  i ) 4 1 1   i 1/4 X 1 2 3 4 Y 1 2 3 4 1/8 1/8 0 0 1/12 1/12 1/ 12 0 1/16 1/16 1/16 1/16        x x y y ij i j p F x y P X x Y y , ( , ) ( , )        2, 2 (2, 2) ( 2, 2) xi yj pi j F P X Y = 1/ 2  P(Xi, Y j) 0 0 0 P.67 例3请自读

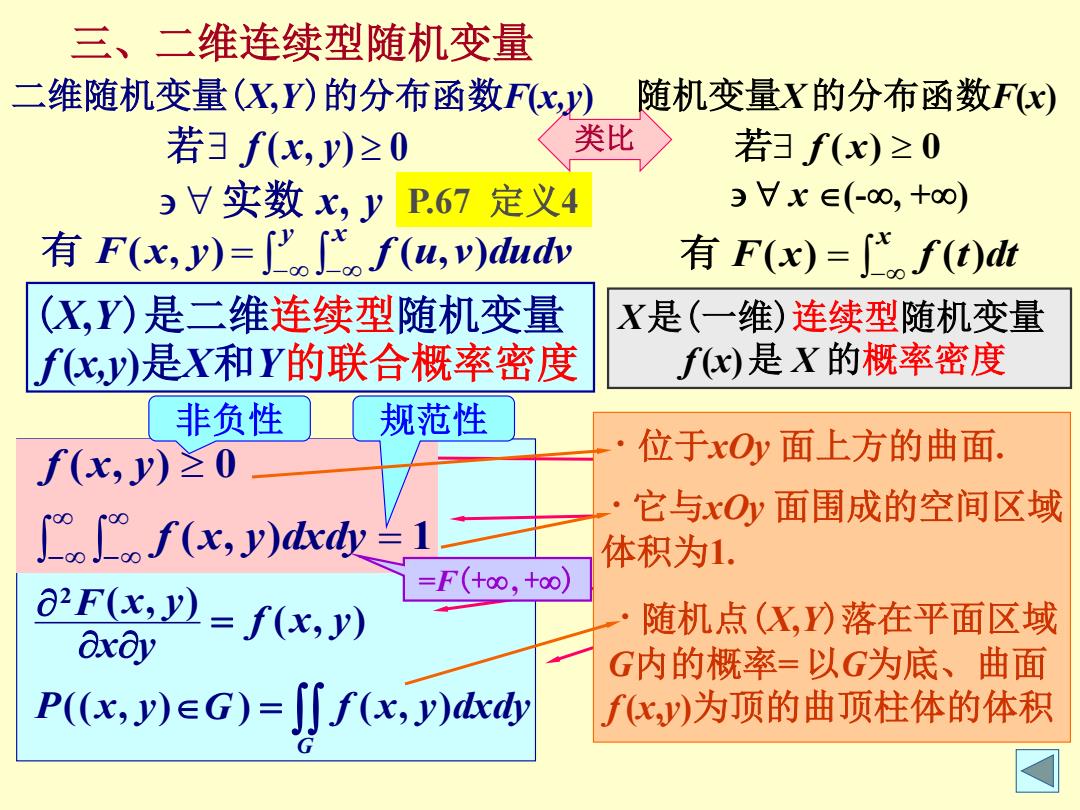
三、二维连续型随机变量 二维随机变量X,Y)的分布函数FK,y) 随机变量X的分布函数Fx) 若3f(x,y)≥0 类比 若]f(x)≥0 H实数K,yP.67定义4 )Vx∈(-0，+∞) 有F(x,y)=f(uv)dud 有F(x)=f(t)dt (X,Y)是二维连续型随机变量 X是（一维）连续型随机变量 fk,)是X和Y的联合概率密度 fx)是X的概率密度 非负性 规范性 f(x,y)≥0 位于xOy面上方的曲面. 它与xOy面围成的空间区域 f(x,y)c兰1 体积为1. O2F(x,y)=f(x,y) =F(+o0,+o0) 随机点(X,)落在平面区域 Oxoy G内的概率=以G为底、曲面 P(K,y)∈G)=Jj小f(x,y) f(xy)为顶的曲顶柱体的体积

  实数 x, y P.67 定义4   x 有 F(x) f (t)dt 若 f (x)  0 (X,Y)是二维连续型随机变量 若 f (x, y)  0 三、二维连续型随机变量 X是(一维)连续型随机变量 类比    y x 有 F(x, y) f (u,v)dudv            b a P a X b f x dx F x f x f x dx f x { } ( ) ( ) ( ) ( ) 1 ( ) 0 P x y G f x y dxdy f x y x y F x y f x y dxdy f x y G                (( , ) ) ( , ) ( , ) ( , ) ( , ) 1 ( , ) 0 2 · 位于xOy 面上方的曲面. ·它与xOy 面围成的空间区域 体积为1. ·随机点(X,Y)落在平面区域 G内的概率=以G为底、曲面 f(x,y)为顶的曲顶柱体的体积         ( , ) 1 ( , ) 0 f x y dxdy f x y =F(+, +) 非负性 规范性   x (-, +) 随机变量X的分布函数F(x) f(x)是 X 的概率密度 二维随机变量(X,Y)的分布函数F(x,y) f(x,y)是X和Y的联合概率密度

例4P.69例4) 设fc,= Ce-2x+,x>0,y>0; 0 其他. 试求： (1)常数C(2)分布函数F(x,y);(3)P(00,y>0 0, 其他. (3)P(0sX≤1,0<Y≤2）=F(1,2)+F(0,0)-F(0,2)-F(1,0) 记为G =(1-e-3)(1-e-8); PX≤)=P(X,Y)∈G)=J∬f(x,y) =126e3t=号

⑶ P(0<X1, 0<Y2)   G F(f1(,x2 , )y)dxdy F(0,0)  F(0,2)  F(1,0) 例4(P.69 例4)         0, . , 0, 0; ( , ) (2 ) 其 他 设 Ce x y f x y x y 试求： ⑴ 常数C; ⑵分布函数F(x, y); ⑶ P(0<X1, 0<Y2)与P(YX). 解 ⑴         1  f (x, y)dxdy 由规范性知： , 12 C  ∴ C=12; ⑵    y x F(x, y) f (u,v)dudv 记为G            x y u v du e dv x y 0 0 (3 4 ) 12 , 0, 0; y o x G            0 , . (1 )(1 ), 0, 0; ( , ) 3 4 其 他 e e x y F x y x y y  x        0 0 (3 4 ) 12 x x y dx e dy . 7 4           0 0 C e 3 dx e 4 dy x y 0 , 其他,  (1e 3 )(1e 8 )； G     G P(XY) P((X,Y) G) f (x, y)dxdy