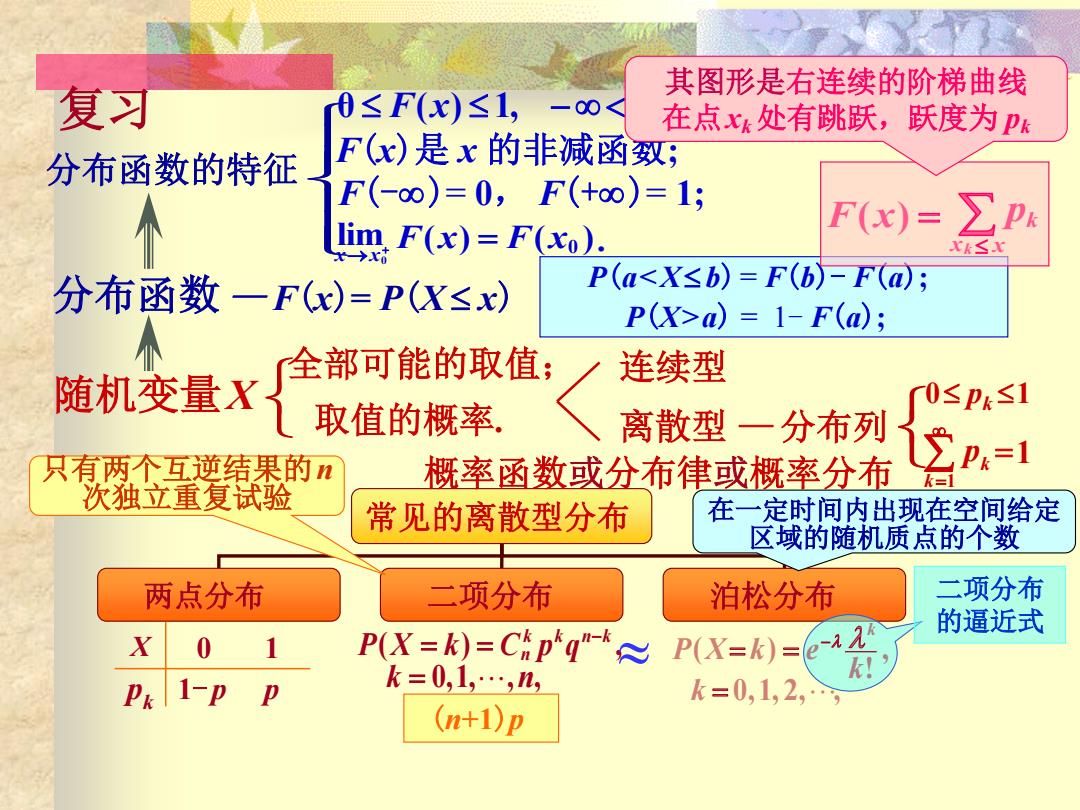
其图形是右连续的阶梯曲线 复习 0≤F(x)≤1, 一0a)=1-F(a); 全部可能的取值; 连续型 随机变量X 取值的概率. 0≤Pk≤1 离散型一分布列 只有两个互逆结果的n 概率函数或分布律或概率分布 P=1 k= 次独立重复试验 常见的离散型分布 在一定时间内出现在空间给定 区域的随机质点的个数 两点分布 二项分布 泊松分布 二项分布 的逼近式 X 0 P(X=k)=Cpq"-≈ P(X=k)=-a2 Pk 1-P p k=0,1,…,n, k=0,1,2, (n+1)p
常见的离散型分布 两点分布 二项分布 泊松分布 0,1, 2, , , ! ( ) k k P X k e k 全部可能的取值; 取值的概率. 随机变量X —分布列 分布函数 概率分布与分布函数的关系? 复习 连续型 离散型 分布函数的特征 概率函数或分布律或概率分布 — F(x)= P(X x) 0 pk 1 0 F(x) 1, x ; F(-)= 0, F(+)= 1; F(x)是 x 的非减函数; P(aa) = 1- F(a); 1 1 k k p ( ) ( ). lim 0 0 F x F x x x 0,1, , , ( ) , k n P X k C p q k k n k n X 0 1 pk 1- p p 只有两个互逆结果的n 次独立重复试验 (n+1)p 二项分布 的逼近式 x x k k F(x) p 其图形是右连续的阶梯曲线 在点xk 处有跳跃,跃度为 pk 在一定时间内出现在空间给定 区域的随机质点的个数

我们介绍了离散型随机变量及其概率分布 只要知道了随机变量的分布函数,就可以计算与 该随机变量有关的事件的概率. 对于离散型随机变量,如果知道了它的分布列, 也就知道了该随机变量取值的概率规律.在这个意义 上,我们说离散型随机变量由它的分布列唯一确定. 下面,我们将向大家介绍另一种类型的随机变量 连续型随机变量的描述方法
在这个意义 上,我们说 对于离散型随机变量,如果知道了它的分布列, 也就知道了该随机变量取值的概率规律. 离散型随机变量由它的分布列唯一确定. 下面,我们将向大家介绍另一种类型的随机变量 我们介绍了离散型随机变量及其概率分布. 只要知道了随机变量的分布函数,就可以计算与 该随机变量有关的事件的概率. —— 连续型随机变量的描述方法

§2.3连续型随机变量 不能象离散型那样,以指定它取每个 值的概率的方式去给出其概率分布 全部可能取值有无穷多,而且充满一个(或若干)区间而不能 一列举 类似于前面对离散型随机变量的讨论,对于连续型随机变 量我们首先关心的是:如何描述它取值的概率规律 分布函数?其取值的概率规律 例1:设有一质点等可能地落入区间[0,2]内, 令X为落 入后这个质点到原点O的距离,求X的分布函数. 解显然X为随机变量,且可能取值充满了区间[0,2], 当x<0时,F(x)=PX≤x)=P(D)=0; 当0≤x<2时,F(x)=P(X≤x)=x/2; 当x≥2时,F(x)=P(X≤)=1. 0, x<0; 故X的分布函数为F(x)={x/2,0≤x<2; 连续函数 F'w)=f)=V2, 0≤x<2; 1,x≥2. 0, 其他. 非负函数可积 =F(x)-F(-o)=∫nft)dt
: 令X为落 入后这个质点到原点 O 的距离, F(x) 解 显然 X 为随机变量, §2.3 连续型随机变量 全部可能取值有无穷多,而且充满一个(或若干)区间而不能一一列举 类似于前面对离散型随机变量的讨论,对于连续型随机变 量我们首先关心的是: 分布函数 其取值的概率规律 例 1 如何描述它取值的概率规律. ? 设有一质点等可能地落入区间[0, 2]内, 求 X 的分布函数. 且可能取值充满了区间[0, 2], 当 x<0 时,F(x)= P(X x) 故 X 的分布函数为 = P( )= 0; 当 0 x<2 时, F(x)= P(X x) = x /2; 当 x2 时,F(x)= P(X x)= P(X<0)+P(0X2)+P(2<Xx) = 0 + 2/2 + 0 = 1. 1, 2. /2, 0 2; 0, 0; ( ) x x x x F x 0, . 1/ 2, 0 2; ( ) 其他 x f x x f (t)dt 非负函数 不能象离散型那样, 以指定它取每个 值的概率的方式去给出其概率分布 1 . . 0 1 2 x F . F(x) F() 可积 连续函数
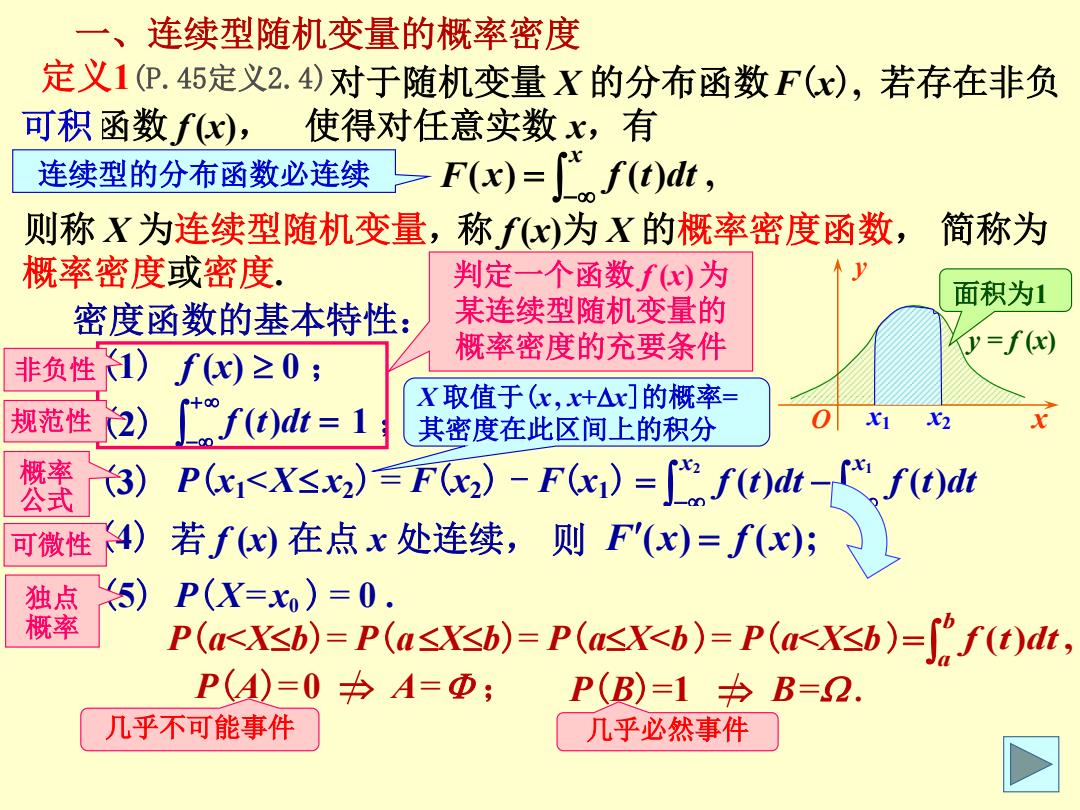
一、连续型随机变量的概率密度 定义1(P.45定义2.4)对于随机变量X的分布函数F(x),若存在非负 可积函数fx),使得对任意实数x,有 连续型的分布函数必连续 -F(x)=f(t)dt, 则称X为连续型随机变量,称f)为X的概率密度函数,简称为 概率密度或密度. 判定一个函数fx)为 面积为1 密度函数的基本特性: 某连续型随机变量的 概率密度的充要条件 =f) 非负性1) fx)≥0; X取值于(x,+△x]的概率= 规范性 2) [f(t)dt=1 其密度在此区间上的积分 率 公式 3) P(c1<X≤x )F)-Fx)=f(di-f(t)d 可微性 4) 若fx)在点x处连续,则F'(x)=f(x); 独 5) P(X=x)=0. 率 P(aKXb)=P(a≤Xb)=P(a≤XKb)=P(aKX≤b)=∫f(t)dt P(A)=0A=Φ; P(B)=1≠B=2. 几乎不可能事件 几乎必然事件
2 1 ( ) ( ) x x f t dt f t dt 简称为 概率密度或密度. 对于随机变量 X 的分布函数F(x), 若存在非负 可积函数 f (x), ( ) ( ) , x F x f t dt 使得对任意实数 x,有 则称 X 为连续型随机变量, 由定义 一、连续型随机变量的概率密度 称 f (x)为 X 的概率密度函数, 定义1(P.45定义2.4) 密度函数的基本特性: (1) f (x) 0 ; ( ) ( ) ( ) (2) f t dt F 1 ; F = 1 - 0 (3) P(x1<X x2) = F(x2) - F(x1) (4) (5) = 0 判定一个函数 f (x)为 某连续型随机变量的 概率密度的充要条件 独点 概率 非负性 规范性 可微性 概率 公式 y O x y = f (x) 面积为1 x1 x2 ( ) ; 2 1 x x f t dt 2 1 1 1 ( ) ( ) ( ) x x x x 若 f (x) 在点 x 处连续, f t dt 则 Ff(xt)dt f (x)f; t dt lim ( 0 0 ) 0 P x X x x x x x x x f x dx 0 0 lim ( ) 0 P(X=x0 ) = 0 . P(a<Xb)= P(aXb)= P(aX<b )= P(a<Xb ) ( ) , b a f t dt 几乎不可能事件 几乎必然事件 P(A)=0 A= ; P(B)=1 B= . X 取值于(x , x+x]的概率= 其密度在此区间上的积分 可积 连续型的分布函数必连续

对fx)的进一步理解: 若x是f(x)的连续点,则 质 lim P(x<X≤x+)= lim f)d lim f(x+4x)=f(x) 4c→0 △x r→0 ∠K r→0 这表明X的密度fx)在x这一点的值,恰好是X落在区间 (x,x+△x]上的概率与区间长度△x之比的极限.如果我们把概率 理解为质量,则f)相当于线密度. 由极限概念知P(x<X≤x+x)≈f(x),它表明随机变量X 取值于区间(x,x+△]的概率近似等于fx)△x;这表明fx)△x在连 续型随机变量理论中所起的作用与P{X=xx}=Pk在离散型随机变 量理论中所起的作用相类似. 注意,密度函数fc)在某点处的值,并不等于X取值的概 率.但这个值越大,则X取a附近的值的概率就越大. 即在某点 密度曲线的高度反映了概率集中在该点附近的程度. 连续型随机变量由它的密度函数所唯一确定.所以,若已知密 度函数,该连续型随机变量的概率规律就得到了全面描述
所以,若已知密 度函数,该连续型随机变量的概率规律就得到了全面描述. 即在某点 密度曲线的高度反映了概率集中在该点附近的程度. 注意,密度函数 f (x) 在某点 a 处的值,并不等于 X 取值的概 率. 这表明 f (x)x 在连 续型随机变量理论中所起的作用与 P{ X= xk}= pk 在离散型随机变 量理论中所起的作用相类似. 它表明随机变量 X 取值于区间(x, x+x]的概率近似等于 f (x)x; 但这个值越大,则 X 取 a 附近的值的概率就越大. 如果我们把概率 理解为质量, 恰好是 X 落在区间 ( x , x+x]上的概率与区间长度 x 之比的极限. 这表明 X 的密度 f (x) 在 x 这一点的值, 若 x 是 f (x) 的连续点,则 x P x X x x x ( ) lim 0 x f t dt x x x x ( ) lim 0 = f (x) 对 f (x) 的进一步理解: lim ( ) 0 f x x x 则 f (x) 相当于线密度. 由极限概念知 P( x X xx) f (x)x , 质量 连续型随机变量由它的密度函数所唯一确定

例2(P.47例2)设随机变量X的概率密度为 A(4x-2x2),0<x<2; ={ (1)确定常数A; 0, 其它, (2)求X的分布函数F(x); (3)求P(0≤X<1),PX1) 解()1=gfdi=0dc+44x-2x2+店0dk=3A,A=g ②))由(①知f=是r-2,0<2: 由概率密度定义知 0. 其它, F()=f()t, 当x<0时,F(x)=0dt=0; 0 x≤0; 当un-产2 当x≥2时,F()=0dt+6(: 1 X≥2. (3) 用分布函数求 用概率密度求 P(0≤X<1)=F(1)-F(O)=7, P0≤X<)=2x-x2)=2 P(X1)=1-F(1)=2: P1)=(x-x2)dx=2
例2(P.47 例2) 设随机变量 X 的概率密度为 0, , (4 2 ), 0 2; ( ) 2 其它 A x x x f x (1) 确定常数A; (2) 求X 的分布函数F(x); 解(1) 1 f (t)dt 2 2 0 2 0 0dx A(4x 2x )dx 0dx , 3 8 A (3) 求 P(0X1). . 8 3 A 由概率密度定义知 ( ) ( ) , x F x f t dt 当 x1)=1-PF((1) X1) 2 1 1. 2 1 P(0X<1)= F(1)-F(0) , 2 1 1 P(X 1) f (x)dx . 2 1 2 1 2 ) 4 3 2 3 ( x x dx 1 0 P(0 X 1) f (xx)dx x )dx 4 3 2 3 ( 2 用概率密度求
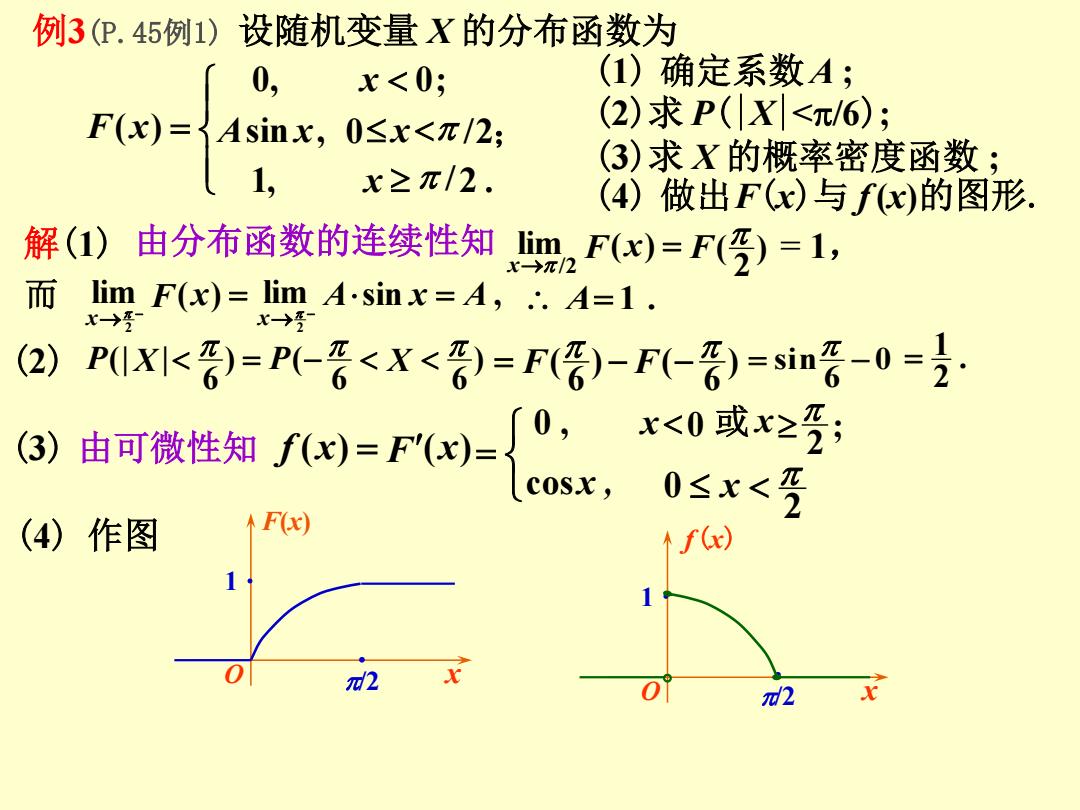
例3(P.45例1)设随机变量X的分布函数为 0, x<0; (1)确定系数A; F(x)=Asinx, 0≤x<π/2; (2)求P(X|<π/6); 1, (3)求X的概率密度函数; x≥π/2. (4)做出F(x)与fx)的图形 解(1)由分布函数的连续性知 Iim2F(x)=F()=1, x-→π/2 lim F(x)=lim A.sinx=A,.A=1. X→ X→ (2) P(XI<)=P(-若<X<)=F()-F(-)=sing-0=克: (3) 由可微性知f)=F(x)=厂0, x<0或x≥; cosx, 0≤x< (4)作图 F(x) f(r) n2 x2
例3(P.45例1) 设随机变量 X 的分布函数为 (1) 确定系数 A ; (2)求 P(|X|</6); 解(1) ) 2 lim ( ) ( /2 F x F x 0 6 sin (3)求 X 的概率密度函数 ; A 1 . 由分布函数的连续性知 ) 6 6 ) ( 6 (| | (2) P X P X ; 2 0 x 或 x ) 6 ) ( 6 ( F F = 1, 1, / 2 . sin , 0 /2 0, 0; ( ) x A x x x F x ; (3) 由可微性知 (4) 作图 . 2 1 0 , cosx , (4) 做出F(x)与 f (x)的图形. lim ( ) lim sin , 2 2 F x A x A x x 而 f (x) F(x) 2 0 x f(x) O x F(x) O x . /2 1 . /2 1

二、几个常见的连续型随机变量 1.均匀分布 假设连续型随机变量X在区间[4,b]上取值,且取值在[a,b]中 任意子区间内的概率仅与这个子区间的长度成正比,而与子区间的 位置无关,即X的取值在[α,b]上具有均等性. 定义1(P.49)若连续型随机变量X的概率密度为 可描述在某区间 上具有等可能 a≤r≤b; 结果的随机试验 0. 其它, f(x) 则称X在[4,b]上服从均匀分布,记作X~U[,b]. 均匀分布的分布函数: 0, x<a; F(d X-0 b-a a≤x<b; 1, x≥b, 典型应用:数值计算中由于小数点后某位小数四舍五入所引起的误差; 两辆公共汽车前后通过某停车站的时间(乘客候车时间)等
= 1 b a dt 而与子区间的 位置无关, f(x) a O b x [ ] 1. 均匀分布 则称 X在[a,b]上服从均匀分布, 0, , , ; 1 ( ) 其它 a x b b a f x 二、 几个常见的连续型随机变量 定义1(P.49) 若连续型随机变量 X 的概率密度为 且取值在[a ,b]中 任意子区间内的概率仅与这个子区间的长度成正比, 即 X 的取值在[a , b]上具有均等性. 假设连续型随机变量 X 在区间[a, b]上取值, 记作 X ~ U[a, b]. 均匀分布的分布函数: x F(x) f (t)dt x a ; a x b ; x a b a dt xb , , b a x a 0, 1 , x b b a dt b a dt 0 F(x) a O b x 1 ba 1 典型应用:数值计算中由于小数点后某位小数四舍五 入所引起的误差; 两辆公共汽车前后通过某停车站的时间(乘客候车时间)等. 可描述在某区间 上具有等可能 结果的随机试验

例4(P.50例5)设某公共汽车站每10分钟有一班车通过,则在任 一时刻到站乘客的候车时间X(单位:分钟)在区间[0,10]上服从均匀 分布,试求乘客候车时间超过6分钟的概率. 解:X~U[a,f时=品, 0≤x≤10; 0, 其它, 所求概率为P{X>6}=”fx)=公k=号. 例5(P.59Ex11)设随机变量X~U[2,5],现对X进行三次独立观测, 求至少有两次观测值大于3的概率. 解XU[2,5,f=得2≤x≤5 则P{X>3}=∫310d=号 0, 其它, 设Y表示对X的观测值大于3的次数,Y=0,1,2,3,则Y~B(3,23), 所求概率为P(P>2)=店P=)=含C2/31V3=费
则在任 一时刻到站乘客的候车时间 X(单位: 分钟)在区间[0, 10]上服从均匀 分布, 解 ∵ X ~U[a, b], 所求概率为 0, 其它, , 0 10; 10 1 ( ) x f x 例4(P.50 例5) 设某公共汽车站每 10 分钟有一班车通过, 试求乘客候车时间超过 6 分钟的概率. P{X 6} f x dx 6 ( ) dx 10 6 10 1 . 5 2 例5(P.59EX11) 设随机变量X~U[2, 5],现对X进行三次独立观测, 求至少有两次观测值大于 3 的概率. 解 ∵ X~U[2, 5], 0, 其它, , 2 5; 3 1 ( ) x f x 则 P{X3} dx 5 3 10 1 . 3 2 设Y表示对X的观测值大于3的次数,Y=0,1, 2, 3,则 Y~B(3, 2/3), 所求概率为 P(Y 2) 3 2 ( ) k P Y k k k k k C 3 3 2 3 (2 / 3) (1/ 3) . 27 20

2.指数分布 定义2若连续型随机变量X的概率密度为 f(x)= [e-, x>0; f(r) 0, x≤0, 其中兄>0为常数,则称X服从参数为入的指数分布, 记为X~E(2). F(x) 指数分布的分布函数: F) x≤0; 0 X 指数分布在可靠性理论中描绘设备工作的可靠时间.有些系统的寿命分布也 可用指数分布来近似,如电子产品或动物寿命的分布,当产品的失效是偶然失效 时其寿命服从指数分布.在排队论中它被广泛地用于描绘等待时间,如电话通 话时间、各种随机服务系统的服务时间、等待时间等.在更新和维修问题中描 绘设备的寿命和维修时间.指数分布是伽玛分布和威布尔分布的特殊情况. 一般地,当随机质点流中在长的时间内出现的质点数服从参数为t的泊松 分布时,其相继出现两个质点的事件间就服从参数为入的指数分布
在更新和维修问题中描 绘设备的寿命和维修时间. 如电话通 话时间、各种随机服务系统的服务时间、等待时间等. 当产品的失效是偶然失效 时其寿命服从指数分布. 在排队论中它被广泛地用于描绘等待时间, 指数分布是伽玛分布和威布尔分布的特殊情况. 有些系统的寿命分布也 可用指数分布来近似, 则称X服从参数为 的指数分布, 指数分布在可靠性理论中描绘设备工作的可靠时间. 其中>0为常数, 记为 X~E(). 2. 指数分布 指数分布的分布函数: F(x) x 0; 0, x 0; 0 , 0 0 x x dx e dx 1 , 0; e x x F(x) O x 1 如电子产品或动物寿命的分布, 一般地, 当随机质点流中在长t 的时间内出现的质点数服从参数为t 的泊松 分布时, 其相继出现两个质点的事件间就服从参数为的指数分布. 0 x e 0 dx = 1 0 x e 定义2 若连续型随机变量 X 的概率密度为 0, 0, 0 ( ) x e x f x x , ; f(x) O x