
复习 上节我们研究了概率的计算问题 舌典概型 直接计算 几何概型 等可能性 有无数值关系? 条件概率 一B发生的条件下A的条件概率P(AB) P(AB) 推算 P(AlB)= P(B) 一 般地不等于A的无条件概率. 什么条件下才会出现P(A)=P(AB)的情形呢? 乘法公式一给出了计算多个事件同时发生的概率, 当P(A1A2Am-1)>0时,有 P(AA2...A)=P(A)P(A2A)P(A3AA2). …P(AmlA1A2…An-1) 在计算概率时经常使用,需要牢固掌握
等可能性 条件概率 乘法公式 — B 发生的条件下 A的条件概率P(A|B) 一般地不等于A的无条件概率. — 给出了计算多个事件同时发生的概率, 复习 古典概型 几何概型 上节我们研究了概率的计算问题 直接计算 推 算 什么条件下才会出现 P(A)=P(A|B)的情形呢? 在计算概率时经常使用,需要牢固掌握. 有无数值关系? 当 P(A1A2…An-1)> 0 时,有 P(A1A2…An)= P(A1)P(A2 |A1)P(A3 |A1A2) „ „ P(An| A1A2…An-1) ( ) ( ) ( | ) P B P AB P A B

事件的独立性 (p.2714 般地P(AB)≠P(A) 例子 将一颗均匀骰子连掷两次,设A={第二次掷出6点}, B={第一次掷出6点},显然P(AB)=P(A), 这表明,事件B发生,并不影响事件A发生的概率. 若P(AB)=P(A),由乘法公式P(AB)=P(B)P(AB)知, P(AB)=P(A)P(B) 反之,若P(AB)=P(A)P(B),且P(B)>0, P(A)=P(AB)/P(B)=P(AP(P23.Th1) 在条件P(B)>0下,P(AB)=P(A)台P(AB)=P(A)P(B). 定义(P.37定义8)若事件A,B满足P(AB)=P(A)P(B),则称事件 A与B相互独立.简称独立. 比用P(AB)=P(A)或P(BA)=P(B)好, 不受P(B)>0或P(A)>0的制约 不可能事件与任一事件都是相互独立的 必然事件/ E
则称事件 A与 B相互独立 . 设 A ={第二次掷出6点}, B ={第一次掷出6点}, 定义(P.37 定义8) 若事件A, B 满足P(AB)= P(A)P(B), 三. 事 件 的 独 立 性 (p.27 1.4) 简称独立 . 不可能事件与任一事件都是相互独立的 一般地 P(A|B)≠ P(A) 例子 将一颗均匀骰子连掷两次, 显然 P(A|B)= P(A), 这表明, 事件B发生, 并不影响事件A 发生的概率. 若 P(A|B)= P(A), P(AB)=P(A)P(B) 必然事件 ⁄ 比用 P(A|B)=P(A) 或 P(B|A)=P(B) 好, 不受P(B)>0 或 P(A)>0的制约 由乘法公式 P(AB)=P(B)P(A|B)知, 反之, 若P(AB)=P(A)P(B), 且P(B)>0, 则 P(A)= P(AB)/P(B)= P(A|B) 在条件 P(B)>0下, P(A|B)= P(A) P(AB)=P(A)P(B). (P23.Th1)

例1从一副不含大小王的扑克牌中任取一张,记A={抽到K}, B={抽到的牌是黑色的},问A、B是否独立? 解 由于P(A)=4/52=1/13, P(B)=26/52=1/2, P(AB)=2/52=1/26. 显见,P(AB)=P(A)P(B), 所以事件A、B独立. 也可以通过计算条件概率去做: 由于P(A)=1/13, P(AB)=2/26=1/13, 显见P(A)=P(AB),所以事件A、B独立 实际应用中住往根据问题的实际意义判断两事件是否独立 例如:甲、乙两人向同一目标射击,记A={甲命中},B={乙命中}, A与B是否独立? 由于“甲命中”并不影响“乙命中”的概即一事件发生与否并不影 帝响另一事件发生的概率),故可认为A与B独立
(即一事件发生与否并不影 响另一事件发生的概率), 记 A={抽到K}, B={抽到的牌是黑色的 }, 显见, P(AB)=P(A)P(B), 由于 P(A)= 4/52 = 1/13 , 所以事件A、B独立. 问A、B是否独立? 解 P(AB) = 2/52 = 1/26. P(B)= 26/52 = 1/2 , 也可以通过计算条件概率去做: 由于 P(A) = 1/13, 显见 P(A)= P(A|B), P(A|B)= 2/26 = 1/13, 所以事件A、B 独立. 实际应用中往往根据问题的实际意义判断两事件是否独立 例如: 甲、乙两人向同一目标射击, A与 B 是否独立? 记 A={甲命中}, B={乙命中}, 由于 “甲命中” 并不影响 “ 乙命中” 的概 率 故可认为 A 与 B 独立 . 例1 从一副不含大小王的扑克牌中任取一张

又如:一批产品共件,从中抽取2件,设A={第i件是合格品}1,2, 若抽取是有放回的,因为第一次抽取的结果不会 影响第二次抽取结果,所以A1与A独立 若抽取是无放回的,因为第一次抽取的结果会影 响到第二次抽取结果,则A1与A2不独立 Th2(P.198) 若两事件A、B独立,则 A与B,A与B,A与B 也相互独立 证仅证A与B独立. 概率的性质 P(AB)=P(A-AB)=P(A)-P(AB) A、B独立 =P(A)-P(A)P(B)=P(A)[1-P(B)] =P(A)P(B) 故A与B独立
因为第一次抽取的结果不会 影响第二次抽取结果, 从中抽取2件, 设Ai={第 i 件是合格品} i=1, 2, 若抽取是有放回的, 因为第一次抽取的结果会影 响到第二次抽取结果, 若抽取是无放回的, 又如:一批产品共n件, 所以 A1与 A2独立. 则 A1与 A2不独立. 易证, 若两事件 A、B 独立,则 A与B, A与B, A与B 也相互独立. 证 仅证A与 B 独立. P(AB) P(A AB) A、B 独立 = P(A) - P(AB) 概率的性质 = P(A)- P(A)P(B) = P(A)[1-P(B)] P(A)P(B) 故A与 B 独立 . Th2(P.198)
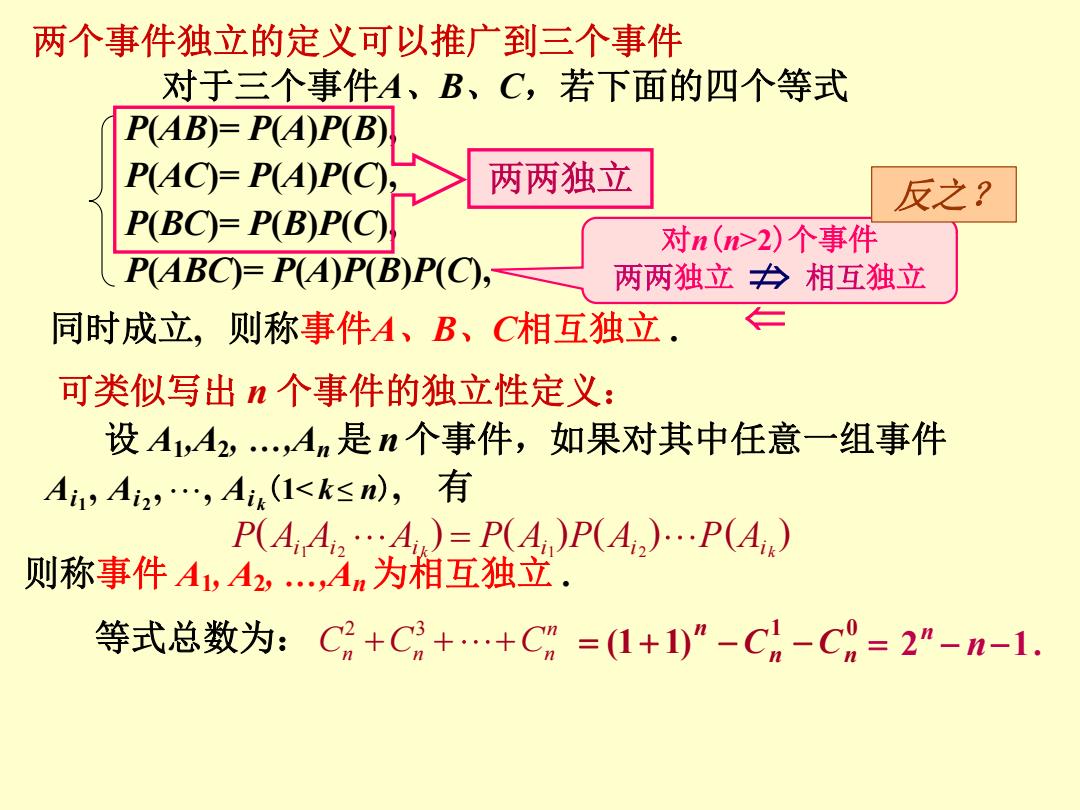
两个事件独立的定义可以推广到三个事件 对于三个事件A、B、C,若下面的四个等式 P(AB)=P(A)P(B) P(AC)=P(A)P(C) 两两独立 反之? P(BC)=P(B)P(C) 对n(n>2)个事件 P(ABC)=P(A)P(B)P(C), 两两独立力相互独立 同时成立,则称事件A、B、C相互独立. 可类似写出n个事件的独立性定义: 设A1,A2,,An是n个事件,如果对其中任意一组事件 Ai,A2,,Ai(1<k≤n),有 P(AA,…A)=P(A)P(A)…P(A) 则称事件A1,A2,,Am为相互独立 等式总数为:C%+C+…+Cm=(1+1)”-Ch-C9=2"-n-1
P(AB)= P(A)P(B), P(AC)= P(A)P(C), P(BC)= P(B)P(C), P(ABC)= P(A)P(B)P(C), 对于三个事件A、B、C,若下面的四个等式 两个事件独立的定义可以推广到三个事件 可类似写出 n 个事件的独立性定义: 则称事件A、B、C相互独立 . 则称事件 A1, A2, …,An 为相互独立 . 等式总数为: 2 3 n C C C n n n 1 0 (1 1) n n n C C 2 n1. n 同时成立, 1 2 1 2 ( ) ( ) ( ) ( ) P A A A P A P A P A i i i i i i k k 设 A1,A2, …,An 是 n 个事件,如果对其中任意一组事件 Ai1 , Ai 2 , , Ai k (12)个事件 两两独立 相互独立 反之?

注意独立性的概念在计算概率中的应用 对于独立事件,许多概率计算可得到简化: 例2三人独立地去破译一份密码,己知各人能译出的概率分别 为1/5,1/3,1/4,问三人中至少有一人能将密码译出的概率是多少? 解将三人编号为1,2,3,记A:={第i个人破译出密码}i=1,2,3 所求为P(A1UA2UA3) 己知P(A1)=1/5,P(A2)=1/3,P(A3)=1/4, P(A1UA2UA3)=1-P(A UA2UA) =1-P(A1A2A3) =1-P(A1)P(A2)P(A3) =1-[1-P(A)][1-P(A2)][1-P(A3)] =1-专3星g-6
P(A1∪A2∪A3 ) 对于独立事件,许多概率计算可得到简化: 例2 三人独立地去破译一份密码, 已知各人能译出的概率分别 为1/5, 1/3, 1/4, 问三人中至少有一人能将密码译出的概率是多少? 解 将三人编号为1, 2, 3, 所求为 P(A1∪ A2∪ A3 ) 记 Ai = {第 i 个人破译出密码 } i =1,2,3 注意独立性的概念在计算概率中的应用 已知 P(A1)= 1/5, P(A2)= 1/3, P(A3)= 1/4, 1 2 1 ( ) P A A An 1 ( ) P A1A2A3 1 ( ) ( ) ( ) P A1 P A2 P A3 = 1-[1-P(A1)][1-P(A2)][1-P(A3)] 0.6 . 5 3 4 3 3 2 5 4 1
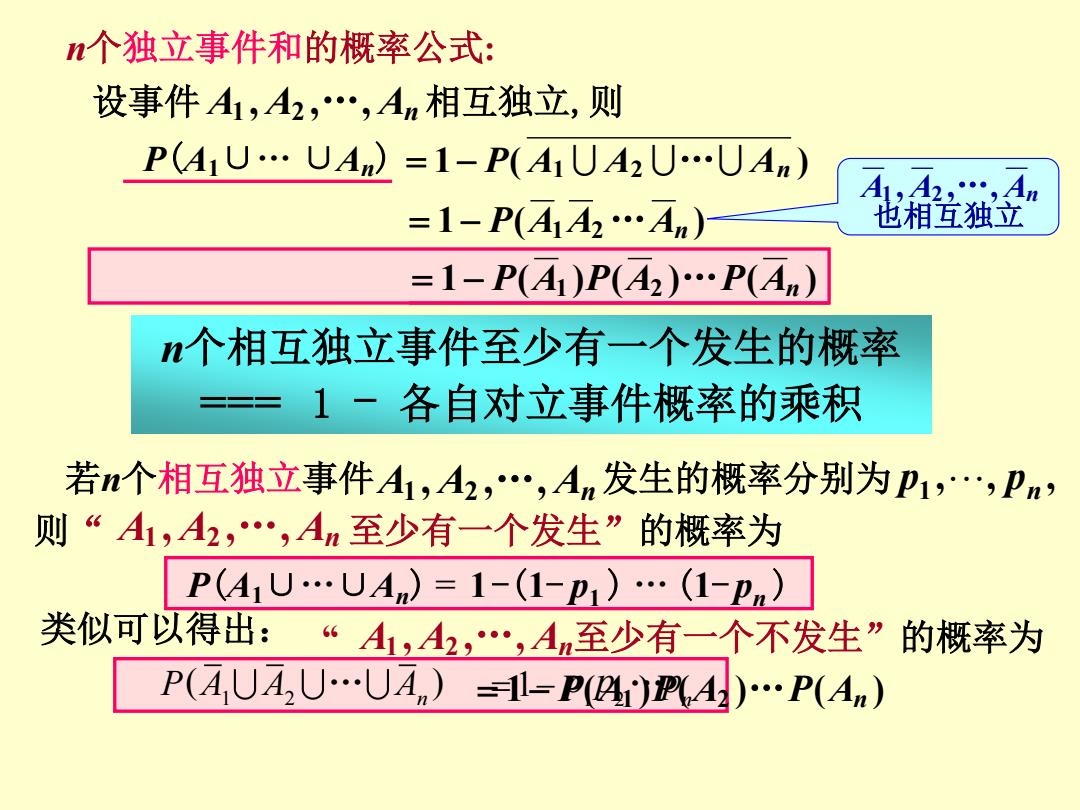
n个独立事件和的概率公式: 设事件A1,A2,…,An相互独立,则 P(A1U…UAm)=1-P(A1UA2U…UAm) A,A2…,An =1-P(A1A2…An) 也相互独立 =1-P(A1)P(A2)…P(An) n个相互独立事件至少有一个发生的概率 1一各自对立事件概率的乘积 若n个相互独立事件A1,A2,…,An发生的概率分别为P1,…,Pm, 则“A1,A2,…,An至少有一个发生”的概率为 P(A1UUAn)=1-(1-p1)…(1-pn) 类似可以得出:“A1,2,,Am至少有一个不发生”的概率为 P(AUA,U..UA)=P(()P(An)
设事件 A1 , A2 , „ , An 相互独立,则 1 P( A1 A2 „ An ) 1 P(A1A2„An ) P(A1∪„ ∪An) 1 P(A1 )P(A2 )„P(An ) 也相互独立 A1 , A2 , „ , An n个相互独立事件至少有一个发生的概率 === 1 - 各自对立事件概率的乘积 , , , 1 n p p 若n个相互独立事件 A1 , A2 , „ , An 发生的概率分别为 则“ A1 , A2 , „ , An 至少有一个发生”的概率为 P(A1∪„∪An) = 1-(1- p1 ) „(1- pn ) 类似可以得出: “ A1 , A2 , „ , An 至少有一个不发生”的概率为 1 2 ( ) P A A A … n 1 P(A1 )P(A2 )„P(An ) n个独立事件和的概率公式: 1 2 1 n p p p …

例3 一玩电子游戏者在一次射击中命中率为p=0.004, 求n次射击过程中击中目标的概率. 解设A={第i次射击时击中目标}i=l,,n 小概率事件 则P(A;)=p=0.004,且A,A2,…,Am相互独立 再设A={击中目标}, 则有A=A 故P(A)=1-P(A1)P(A2)…P(An) =1-(1-p)" =1-0.996". 当n=500时,P(A)=0.865. 只要P(4)=p<1,就有mP(4)=I1-(1-p)”]=1 只要你坚持重复地做,发生概率再小的事件总会发生
例3 一玩电子游戏者在一次射击中命中率为p = 0. 004 , 求n 次射击过程中击中目标的概率 . 解 设 Ai ={ 第 i 次射击时击中目标 } i =1,„ ,n , 则 P(Ai )= p = 0. 004 , 则有 且 A1 , A2 , „ , An 相互独立, 再设 A ={ 击中目标 }, , n i A Ai 1 故 P(A) 1 P(A1)P(A2)P(An) n 1 (1 p) 1 0.996 . n 当 n = 500 时, P(A)= 0. 865 . 小概率事件 只要 P(A)= p<1, lim ( ) lim [1 (1 ) ] n n n P A p 就有 = 1 只要你坚持重复地做,发生概率再小的事件总会发生

例4 设A、B、C是三个事件,且P(A)=0.3,P(C)=0.6, P(BA)=0.4,P(BUC)=0.72,B与C相互独立,求P(AUB). 分析P(MUB)=P(A)+P(B)-P(4B2P4D+B,P(M)P(BA) =P(A)P(BA) 解由于B与C独立, P(BUC)=P(B)+P(C)-P(B)P(C) =P(B)[1-P(C)]+P(C) =0.4P(B)+0.6=0.72,→P(B)=0.3, 所以P(AUB)=P(A)+P(B)-P(A)P(BA) =0.3+0.3+0.3×0.4=0.48
例4 设 A、B、C 是三个事件,且 P(A)=0.3, P(C)= 0.6 , P(B|A)= 0.4 , P(B∪C)= 0.72 , B与 C相互独立,求 P(A∪B ). 解 由于 B与 C独立, 故 P(B∪C)= P(B)+ P(C) -P(B)P(C) = P(B)[1-P(C) ] + P(C) = 0.4 P(B) + 0.6 = 0. 72 , P(B)= 0. 3 , 分析 P(A∪B)=P(A)+ P(B)-P(AB) = P(A)P(B|A) = P(A)+ P(B) -P(A)P(B|A) ? 所以 P(A∪B)=P(A)+ P(B)-P(A)P(B|A ) = 0. 3 + 0. 3 + 0.30. 4 = 0. 48
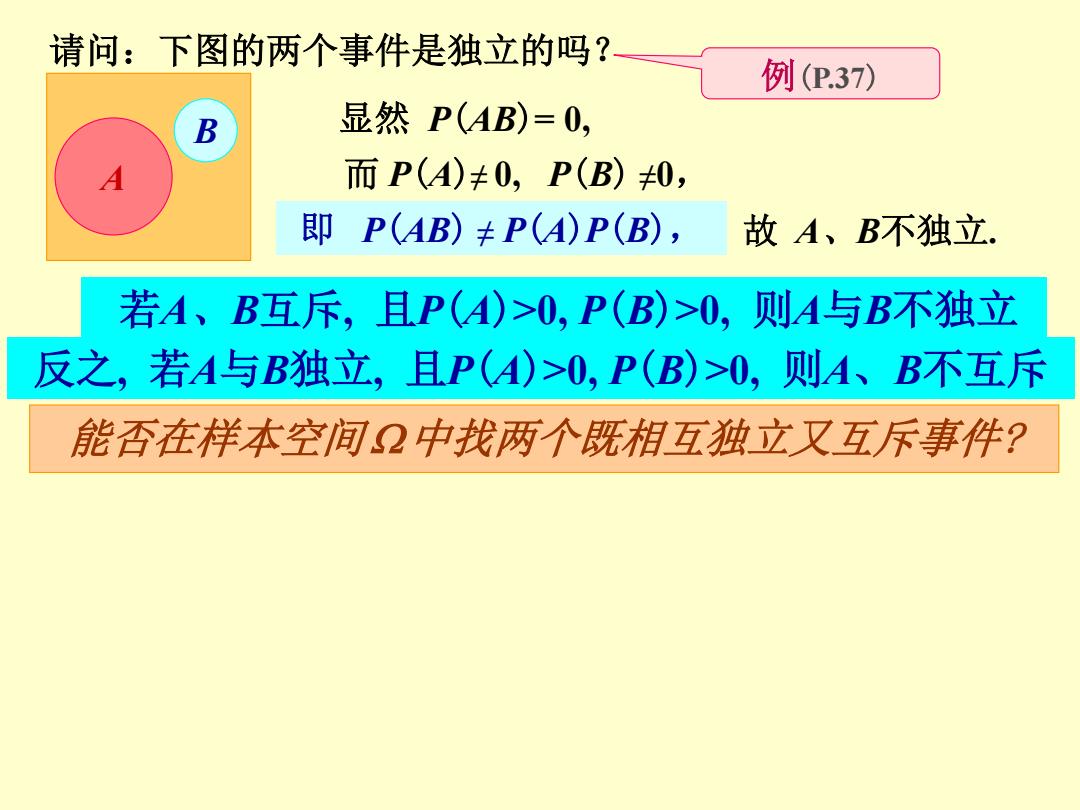
请问:下图的两个事件是独立的吗? 例(P.37) B 显然P(AB)=0, 而P(A)≠0,P(B)0, 即P(AB)≠P(A)P(B), 故A、B不独立. 若A、B互斥,且P(A)>0,P(B)>0,则A与B不独立 反之,若A与B独立,且P(A)>0,P(B)>0,则A、B不互斥 能否在样本空间2中找两个既相互独立又互斥事件?
请问:下图的两个事件是独立的吗? A B 显然 P(AB)= 0, 而 P(A)≠ 0, P(B) ≠0, 即 P(AB) ≠ P(A)P(B), 故 A、B不独立. 例(P.37) 若A、B互斥, 且P(A)>0, P(B)>0, 则A与B不独立 反之, 若A与B独立, 且P(A)>0, P(B)>0, 则A、B不互斥 能否在样本空间中找两个既相互独立又互斥事件?