上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）08、多维随机变量及分布 §3.3 二维随机变量的条件分布 §3.4 随机变量的独立性

复习X与Y的联合分布F(x,y)=P{X≤x,Y≤y} P{1<X≤x2,y1<Y≤y2}=F(2,y2)-F(x2,JM1)+F(,1)-F(1,y2) 离散型一 联合分布列P{X=x,Y=yj=Pi,j=1,2,… 联 F(x,y)=P{X≤x,Y≤y}=∑P 分布 xi≤x,yi≤y 函数 连续型 联合概率密度 02F(x,y)=f(x,y) Oxoy F(x,y)=∫」f(u,v)dudw P((x,y)EG=(,y)dd X,)关于X和Y的边缘分布Fx(x)=F(x,o),F(y)=F(+o,y) 离散型一边缘分布列 关于x的PP=PX=iFx()P 边缘 分布 关于Y的p=PH=P{Y=y,F(x)=P ≤y 函数 关于X的fx(x)=f(x,y) 连续型 边缘概率密度 Fx(x)=∫f(u,y)y]u 关于y的f(y)=fx,y)k Fy(y)=f(x,v)dxldv

复习 联合 分布 函数    离散型 连续型 { , } ( , ) ( , ) ( , ) ( , ) P x1  X  x2 y1 Y  y2  F x2 y2 F x2 y1  F x1 y1 F x1 y2 —— 联合分布列 —— 联合概率密度 i j pij P{Xx , Y y } i, j 1,2,         x x y y ij i j F x y P X x Y y p , ( , ) { , }    y x F(x, y) f (u,v)dudv P x y G f x y dxdy f x y x y F x y G        {( , ) } ( , ) ( , ) ( , ) 2 边缘 分布 函数    离散型 连续型 —— 边缘分布列 —— 边缘概率密度    f x  f x y dy X ( ) ( , )    f y  f x y dx Y ( ) ( , ) X 与Y 的联合分布 F(x, y)  P{X x, Y  y} (X,Y)关于X 和Y 的边缘分布 F (x)  F(x,), X F ( y) F( , y) Y   关于X 的 关于Y 的 关于X 的 关于Y 的 { }, 1 i j i ij p   p  P X  x    { }, 1 i i j ij p   p  P Yy        y y Y j j F ( x) p     x x X i i F ( x) p       y Y F ( y) [ f (x,v)dx]dv       x FX (x) [ f (u, y)dy]du

复习 两个常见的二维分布 1.均匀分布 后，x时=G; G是平面上的有界区域 0, 其它， S为其面积. 2.正态分布 (X,)~N(41,,2,o,p). )=2πGg2,1-2e2Fp阿ay2p)a2H(1 -0<X<十+0，-0<y<+0 二维均匀分布的两个边缘密度未必是均匀分布 二维正态分布的两个边缘密度仍是正态分布

复习 两个常见的二维分布 1. 均匀分布       0 , , ; , ( , ) 1 ( , ) 其它 x y G f x y S G是平面上的有界区域 S为其面积. 2. 正态分布 (X,Y)～N(  ,  , , ,  ). 2 2 2 2 1 1 二维均匀分布的两个边缘密度未必是均匀分布 二维正态分布的两个边缘密度仍是正态分布 x,  y [( ) 2 ( )( ) ( ) ] 2 (1 ) 1 2 2 2 2 2 1 1 2 1 1 2                   x x y y e2 2 2 1 1 ( , )      1 f x y

我们与一维情形相对照，采用类比和转化的手段 介绍了二维随机变量的联合分布、边缘分布. 联合分布和边缘分布的关系： 由联合分布可以确定边缘分布； 但由边缘分布一般不能确定联合分布. 二维随机变量的两个随机变量之间的关系？ 条件概率 独立性

联合分布和边缘分布的关系: 我们与一维情形相对照，采用类比和转化的手段, 介绍了二维随机变量的联合分布、边缘分布. 由联合分布可以确定边缘分布; 但由边缘分布一般不能确定联合分布. 二维随机变量的两个随机变量之间的关系？ 条件概率 独立性

§3.3二维随机变量的条件分布 在第一章中，我们介绍了条件概率的概念 在事件B发生的条件下事件A发生的条件概率 P(AB 推广到 P(A B) P(B 随机变量 设有两个随机变量X,Y,在给定Y取某个 或某些值的条件下，求X的概率分布. 这个分布就 身高Y 例如，考虑某大学的全体学生， 是条件分布 从其中随机抽取一个学生，分别以X和Y表示其 体重和身高.则X和Y都是随机变量，它们都有一 定的概率分布. 体重X

在事件B 发生的条件下事件A 发生的条件概率 设有两个随机变量X, Y ， 这个分布就 是条件分布 随机变量 推广到 ( ) ( ) ( | ) P B P AB P A B  例如,考虑某大学的全体学生, 则X 和Y 都是随机变量,它们都有一 定的概率分布. 在第一章中，我们介绍了条件概率的概念 体重X 身高Y 从其中随机抽取一个学生，分别以X 和Y 表示其 体重和身高. 在给定 Y 取某个 或某些值的条件下,求 X 的概率分布. §3.3 二维随机变量的条件分布

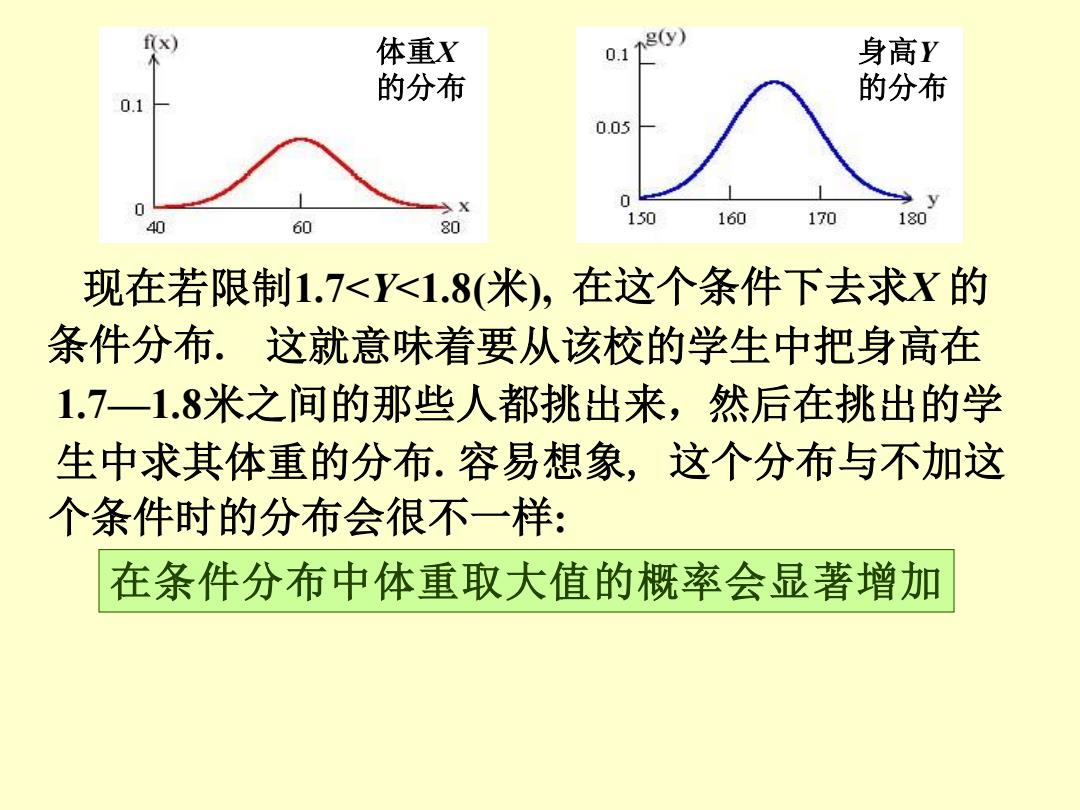
f(x) 体重X g(y) 0.1 身高Y 的分布 的分布 0.1 0.05 0 40 60 80 150 160 170 180 现在若限制1.7<Y<1.8(米)，在这个条件下去求X的 条件分布.这就意味着要从该校的学生中把身高在 1.7一1.8米之间的那些人都挑出来，然后在挑出的学 生中求其体重的分布.容易想象，这个分布与不加这 个条件时的分布会很不一样： 在条件分布中体重取大值的概率会显著增加

在这个条件下去求X 的 条件分布. 容易想象, 这个分布与不加这 个条件时的分布会很不一样: 在条件分布中体重取大值的概率会显著增加 现在若限制1.7<Y<1.8(米), 这就意味着要从该校的学生中把身高在 1.7—1.8米之间的那些人都挑出来，然后在挑出的学 生中求其体重的分布. 体重X 的分布 身高Y 的分布

一、离散型随机变量的条件分布 定义1设X,)是二维离散型随机变量，对于固定的j, 若边缘分布P(Y=)=p>0, 则称 P(X=x;Y=y;)= P(X=xi,Y=Yj)= Pij P(Y=yj) i=1,2,… 为在Y=y,条件下，随机变量X的条件分布列. 类似定义在X=x:条件下随机变量Y的条件分布列： P(Y=yjX=x;)= Pij 认作为条件的那个随机变量的取值是给定的 Pi。 实际上是第一章中条件概率概念在另一种形式下的重复 显然P(X=x|Y=y)≥0,1,2，… 含PX=x=W=2=1 如同条件概率是一种概率，从而具有概率的一切性质，条件 分布列是一种分布列，它具有分布列的一切性质

实际上是第一章中条件概率概念在另一种形式下的重复 定义1 设(X,Y)是二维离散型随机变量， 认作为条件的那个随机变量的取值是给定的 类似定义在 X = xi 条件下随机变量 Y 的条件分布列: 一、离散型随机变量的条件分布 条件 分布列是一种分布列，它具有分布列的一切性质. 如同条件概率是一种概率，从而具有概率的一切性质， (  |  )  0, 显然 P X xi Y yj i=1,2,…      1 ( | ) i P X xi Y y j 联合分布列 边缘分布列 j i j p p   为在Y = yj条件下，随机变量 X 的条件分布列.     i i j j i p p P(Y y X x ) P(X = xi | Y= yj )= ( ) ( , ) j i j P Y y P X x Y y    i=1,2, … 则称      1 1 i ij j p p = 1 对于固定的 j， 若边缘分布P(Y = yj )= p·j > 0

例1P.74例1)一袋中装有两只白球，三只红球， 有放回地连续摸 两次，设随机变量 1,第一次摸出白球 X= Y= 「1，第二次摸出白球 0,第一次摸出红球 0,第二次摸出红球 试求条件X=1下随机变量Y的及Y=0下X的条件分布.先求联合分布列 和边缘分布列 解依题意有PX,X-0)- PX=0x若 P(X=1,Y=0)=P(X=0,Y=1)= ×3 6 5 25 ;P(Y=jX=1)= Py 所以X和Y的联合分布列 2/5 及边缘分布列为 X P(X=iY=0)= Pio 0 1 P.j P.0 3/5 0 9/25 6/25 条件X=1下的 YX=1 0 1 3/5 1 6/25 4/25 2/5 条件分布列为 Pk 3/5 21/5 i 3/5 2/5

有放回地连续摸 两次,   1 1 p p j 解 依题意有 例1(P.74 例1) 一袋中装有两只白球,三只红球, 所以X 和Y 的联合分布列 试求条件X=1下随机变量Y 的及Y=0下X的条件分布. ; 25 9 5 3 5 3 P(X0, Y0)    设随机变量     0, . 1, 第一次摸出红球 第一次摸出白球； X     0, . 1, 第二次摸出红球 第二次摸出白球； Y ; 25 4 5 2 5 2 P(X 1, Y1)    X Y 0 1 0 1 9/25 6/25 6/25 4/25 p• j pi• 3/5 2/5 3/5 2/5 P(Y j X1) . 3 / 5 pi0  ; 2 / 5 1j p  及边缘分布列为 0 0 ( 0 )     p p P X i Y i Y|X=1 0 1 pk 3/5 2/5 条件X=1下的 条件分布列为 先求联合分布列 和边缘分布列 . 25 6 5 3 5 2 P (X1, Y0)  P(X0, Y1)   

求二维离散型随机变量的条件分布列， 需知边缘分布和联合分布. X、Y的条件分布列分别为： P(X=xi|Y=yj)= P.j P(Y=yj|X=x;)= Pis 如何求条件分布函数？ 在已知Y=y下， X的条件分布函敏为：Ex(cy六，三P, y的条件分布函数为：FaxU六，三 在已知X=x,下

求二维离散型随机变量的条件分布列, 需知边缘分布和联合分布. 如何求条件分布函数？     i ij j i p p P(Y y | X x ) j ij i j p p P X x Y y  (  |  )  X 、Y 的条件分布列分别为: 在已知 Y = yj 下, X 的条件分布函数为: 在已知 X = xi 下, Y 的条件分布函数为: ( | ) { | } X|Y j i F x y  P X  x Y  y     y y ij i Y X i j p p F y x 1 ( | ) | { i | j } x x P X x Y y i      { } { , } j j i P Y y P X x Y y         x x ij j i p p 1

二、连续型随机变量的条件分布 设(X,)是二维连续型随机变量，由于x,y,P{X=x}=0,P{Y=y}=0, 所以不能直接用条件概率公式得到条件分布，下面我们用极限工具 给出条件概率密度的定义： 定义2若极限imP(X≤xly<Y≤y+)=im P(X≤x,y<Y≤y+) 0+ 8→0+ P(y<Y≤y+) 存在，则称它为条件Y=y下X的条件分布函数，记为FxIy(cy). 设(X,)的分布函数为F化，y),概率密度为f化，y),若f(x,y)连续， 则其边缘密度函数fx(x),f,y)也连续， nf(山，Jy)du Fxy(xly)=lim [F(x,Jy+)-F(K,y/ε F(x,y) -→0 [Fx(y+E)-F(y)]/ε F(y) fy(y) 则条件Y=y下X的条件密度为 x(x)= f(x,) 类条概公式 f(y) 类似地，条件X-=x下Y的条件分布函数为(LG,)d fx(x) 条件X=x下Y的条件密度为nx(vlx)= f(x,y) f(x f(x,y)=fxr(x|y)fr(y)=fyx(yx).fx(x) fxir(xly)=Ix(x)fnx(ylx) fy(y)

类条概公式 设(X,Y)的分布函数为F(x, y), 概率密度为 f (x, y), 由于x, y, P{X=x}=0,P{Y=y}=0, 所以不能直接用条件概率公式得到条件分布， 类似地,条件 X=x 下Y 的条件分布函数为 定义2 若极限 若 f (x, y)连续， ; ( ) ( , ) | ( | ) f y f x y f x y Y 则条件Y=y下X 的条件密度为 X Y  二、连续型随机变量的条件分布 设(X,Y)是二维连续型随机变量, ( ) ( , ) ( | )                P y Y y P X x y Y y P X x y Y y 下面我们用极限工具 给出条件概率密度的定义:     0 0 lim lim   存在，则称它为条件Y=y下X的条件分布函数， 则其边缘密度函数 fX (x), fY (y) 也连续， ( ) ( , ) ( | ) lim 0 |             P y Y y P X x y Y y FX Y x y FY ( y  )  FY ( y) F(x, y )F(x, y) ( ) ( , ) F y F x y Y y    ( ) ( , ) f y f u y du Y x   . ( ) ( , ) ( | ) | f x f x y f y x X Y X  ， ( ) ( , ) | ( | ) f x f x v dv F x y X y Y X   条件X= x下Y的条件密度为 记为 FX|Y(x|y).   [ ] / [ ]/ ( , ) ( | ) ( ) f x y f | x y f y X Y Y   ( | ) ( )  fY |X y x  fX x ( ) ( ) ( | ) ( | ) | | f y f x f y x f x y Y X Y X X Y 

例2P.76例2)设（化，力的概率密度为fx,y)={ 6，x2≤y≤x,0≤x≤1， 0,其他 求条件概率密度fxr(xy)和fx(yx). 解由类条概公式，应先求两个边缘密度fx心)，fy): 国-={6英 0, 其他. 因避ow-版-8-g7: 其他. 当y0和21时，fr)=0,∴fx(x)= fy(y) 不存在， 挡当01时，f川=少 其他. 同理，当x≤0和x21时，x(w)=0,x(川)=不存在， (x) 当0<cI时，xU1=,sxs片 0, 其他

解 例2(P.76例2) 设(X,Y)的概率密度为 ( | ) ( | ) . fX|Y x y 和 fY|X y x         0, . , 0 1, 6, ( , ) 2 其他 x y x x f x y 同理, 求条件概率密度         0, . 6 , ; 其他 dx y x y y y 由类条概公式， 当 y0 和 y1时，  fY ( y) 0 , 0 x y       ; 2 x y x    fX (x)  f (x, y)dy y=x y=x 2 应先求两个边缘密度 x  y fX (x), fY (y)：  ， x x dy 2 6 0, 其他 . 6( ) , x x2    fY ( y)  f (x, y)dx 6( y  y) , ( ) ( , ) ( | ) | f y f x y f x y Y  X Y          0, . , ; 1 ( | ) 2 | 其 他 x y x f X Y x y y y 不存在, 当 0<y<1时， 同理, f (x) 0 , 当 x0 和 x1时，  X ( ) ( , ) ( | ) | f x f x y f y x X  Y X         0, . , ; 1 ( | ) 2 | 其 他 y x y f y x x x 当 0<x<1时， Y X 不存在