
第11章协整与误差修正模型 11.1 协整与误差修正模型的基本定义 11.2 Engle-Granger协整分析方法 11.3 向量ADF模型与协整分析 11.4 向量误差修正模型(VECM) 11.5 确定性趋势与协整分析 11.6 Johansen协整分析方法 11.7 VECM的估计与统计推断 11.8 Johansen协整分析方法的应用
第11章 协整与误差修正模型 11.1 协整与误差修正模型的基本定义 11.2 Engle-Granger协整分析方法 11.3 向量ADF模型与协整分析 11.4 向量误差修正模型(VECM) 11.5 确定性趋势与协整分析 11.6 Johansen协整分析方法 11.7 VECM的估计与统计推断 11.8 Johansen协整分析方法的应用

11.1协整与误差修正模型的基本概 念 协整分析是基于非平稳序列基础 之上的,而利用非平稳序列进行回归, 经常会出现伪回归现象。而另外一种 情况却是更具有应用价值的协整关系
11.1 协整与误差修正模型的基本概 念 协整分析是基于非平稳序列基础 之上的,而利用非平稳序列进行回归, 经常会出现伪回归现象。而另外一种 情况却是更具有应用价值的协整关系

11.1.1伪回归 对于经典线性回归模型,如: y,=c+Bx,+u, (11.1) 除了对随机扰动项的独立一致性分 布要求之外,一般都要求回归变量, 和y,为平稳时间序列
11.1.1 伪回归 对于经典线性回归模型,如: (11.1) 除了对随机扰动项的独立一致性分 布要求之外,一般都要求回归变量 和 为平稳时间序列。 t t t y c x u = + + t y t x

伪▣归(spurious regression) 就是指变量之间本来并不存在真正的关 系,而是由于变量都是趋势(非平稳) 序列造成的虚假显著性关系
伪回归(spurious regression) , 就是指变量之间本来并不存在真正的关 系,而是由于变量都是趋势(非平稳) 序列造成的虚假显著性关系

在介绍伪回归概念的时候,一般 都使用非平稳序列回归来进行演示。我 们这里使用计算机模拟生成两个观测值 为241个的带截距项的随机游走序列: y=1.5+y1+4,4,:NID(0,1) x,=1.2+x-1+Y,y,:WID(0,1)(11.2) 其中:4,:NID0,)表示服从正态一致性分 布、均值为0、方差为1的随机扰动项
在介绍伪回归概念的时候,一般 都使用非平稳序列回归来进行演示。我 们这里使用计算机模拟生成两个观测值 为241个的带截距项的随机游走序列: (11.2) 其中: 表示服从正态一致性分 布、均值为0、方差为1的随机扰动项。 1 1 1.5 , (0,1) 1.2 , (0,1) t t t t t t t t y y u u NID x x v v NID − − = + + = + + : : (0,1) t u NID :
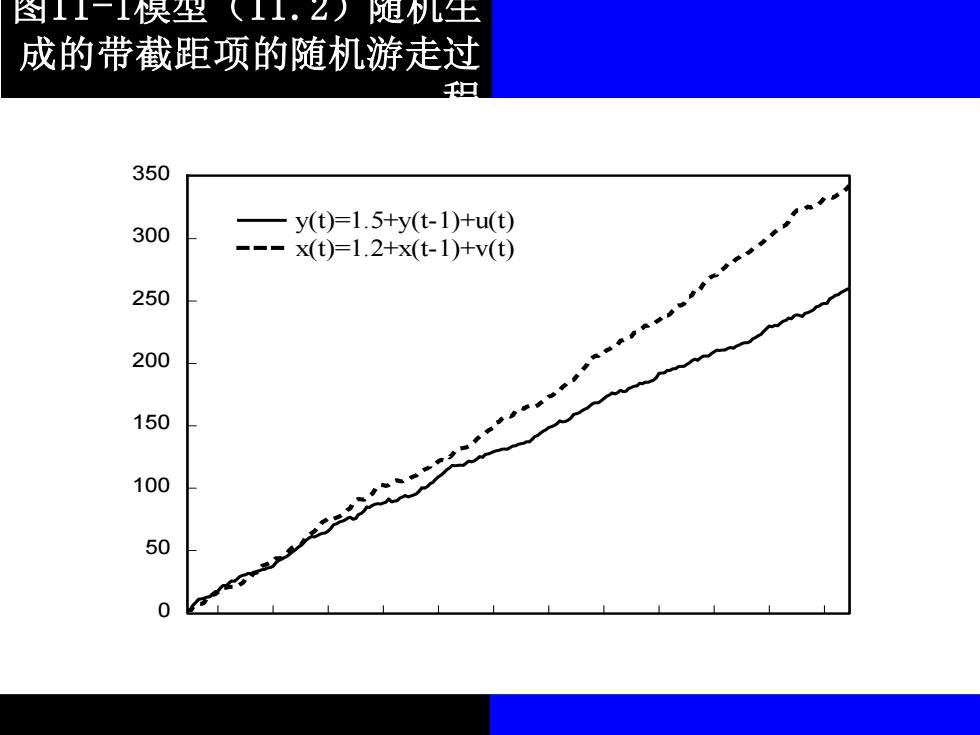
图11一1悞型(11.么)㸖儿任 成的带截距项的随机游走过 工口 350 300 一y(t)=1.5+y(t-1)+u(t) ---xt)=1.2+x(t-1)+v() 250 200 150 100 50 0
图11-1模型(11.2)随机生 成的带截距项的随机游走过 程 0 50 100 150 200 250 300 350 y(t)=1.5+y(t-1)+u(t) x(t)=1.2+x(t-1)+v(t)
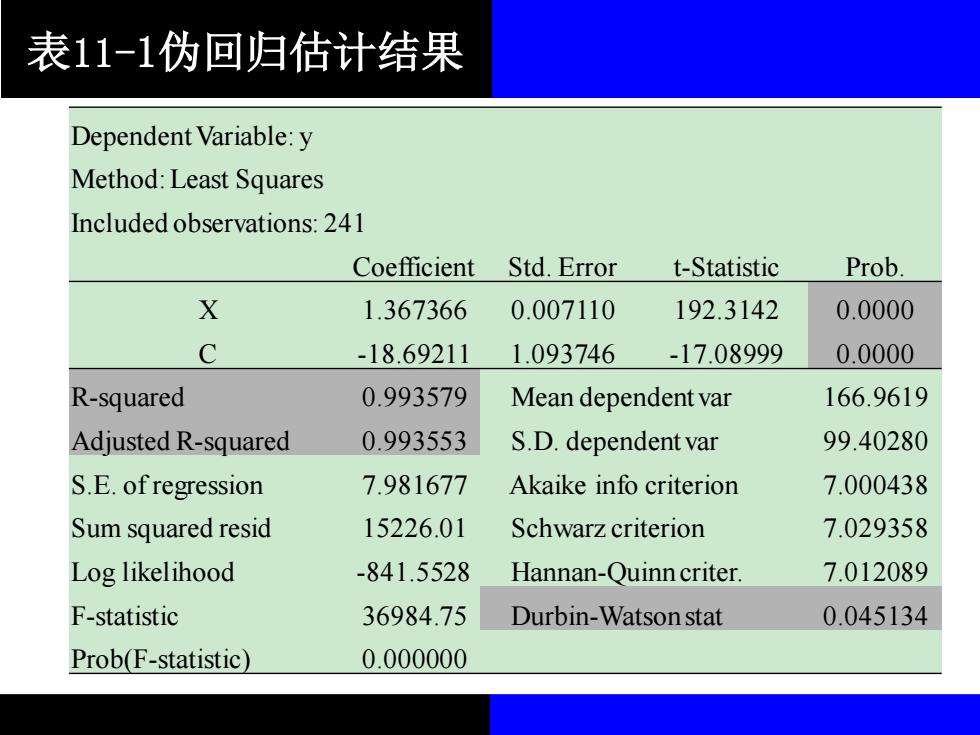
表11-1伪回归估计结果 Dependent Variable:y Method:Least Squares Included observations:241 Coefficient Std.Error t-Statistic Prob. X 1.367366 0.007110 192.3142 0.0000 C -18.69211 1.093746 -17.08999 0.0000 R-squared 0.993579 Mean dependent var 166.9619 Adjusted R-squared 0.993553 S.D.dependent var 99.40280 S.E.ofregression 7.981677 Akaike info criterion 7.000438 Sum squared resid 15226.01 Schwarz criterion 7.029358 Log likelihood -841.5528 Hannan-Quinn criter. 7.012089 F-statistic 36984.75 Durbin-Watson stat 0.045134 Prob(F-statistic) 0.000000
表11-1伪回归估计结果 Dependent Variable: y Method: Least Squares Included observations: 241 Coefficient Std. Error t-Statistic Prob. X 1.367366 0.007110 192.3142 0.0000 C -18.69211 1.093746 -17.08999 0.0000 R-squared 0.993579 Mean dependent var 166.9619 Adjusted R-squared 0.993553 S.D. dependent var 99.40280 S.E. of regression 7.981677 Akaike info criterion 7.000438 Sum squared resid 15226.01 Schwarz criterion 7.029358 Log likelihood -841.5528 Hannan-Quinn criter. 7.012089 F-statistic 36984.75 Durbin-Watson stat 0.045134 Prob(F-statistic) 0.000000

随机生成的这两个变量,虽然并没 有什么经济理论能够说明它们之间存在 一定的联系,但回归估计结果却显示, 模型中的系数都具有统计显著性,说明 二者存在显著的线性关系。并且,表9 1中的回归结果还显示,模型拟合得几 近完美,R高达0.99,而DW统计量又非 常小,只有0.045!这是典型的伪回归 特征
随机生成的这两个变量,虽然并没 有什么经济理论能够说明它们之间存在 一定的联系,但回归估计结果却显示, 模型中的系数都具有统计显著性,说明 二者存在显著的线性关系。并且,表9- 1中的回归结果还显示,模型拟合得几 近完美, 高达0.99,而DW统计量又非 常小,只有0.045!这是典型的伪回归 特征。 2 R

但是,并不是所有非平稳序列之间 都没有一定的联系,有一种特殊情况, 即非平稳时间序列的线性组合是平稳序 列,这个时候,我们说这些非平稳时间 序列之间存在长期的均衡关系,这就是 协整关系。协整关系与伪回归不同,因 为协整刻画了确实存在内在联系的经济 变量之间的长期关系
但是,并不是所有非平稳序列之间 都没有一定的联系,有一种特殊情况, 即非平稳时间序列的线性组合是平稳序 列,这个时候,我们说这些非平稳时间 序列之间存在长期的均衡关系,这就是 协整关系。协整关系与伪回归不同,因 为协整刻画了确实存在内在联系的经济 变量之间的长期关系

11.1.2协整的基本概念 对于多个非平稳时间序列,有一种 特殊的情况,就是由这几个非平稳时间 序列变量的线性组合形成的变量,是平 稳的序列。在这种情况下,我们说这些 非平稳时间序列存在协整关系
11.1.2 协整的基本概念 对于多个非平稳时间序列,有一种 特殊的情况,就是由这几个非平稳时间 序列变量的线性组合形成的变量,是平 稳的序列。在这种情况下,我们说这些 非平稳时间序列存在协整关系