
5.4样本自相关与部分自相关函数 5.4.1样本自相关函数(SACF) 卫=多 三1 T 62= (y-) t=1 ∑(y,-)y,-,-) →p 多-
5.4 样本自相关与部分自相关函数 5.4.1样本自相关函数(SACF) 1 2 2 1 1 1 j 0 2 1 1 1 ˆ ( ) 1 ˆ ( )( ) ( )( ) ˆ ˆ ˆ ( ) T t t T t t T j t t j t j T t t j j t j T t t j y y T y y T y y y y T y y y y y y = = − = + − = + = + = = − = − − − − = = −

Ljung和Box(1978)Q-统计量 0=空品
Ljung 和Box (1978) Q-统计量 2 1 ( 2) k j j Q T T T k = = + −

5.4.2样本部分自相关函数(SPACF) 在EViews软件中,样本部分自相关函 数的求解过程通过下面的步骤实现: 1)利用样本数据和SACF的模型求出 ∑(y-y1-) t1 产o 0y-列 =1
5.4.2 样本部分自相关函数(SPACF) 在EViews软件中,样本部分自相关函 数的求解过程通过下面的步骤实现: 1)利用样本数据和SACF的模型求出 1 1 1 1 1 2 0 1 1 ( )( ) ˆ ˆ ˆ ( ) T t t t T t t y y y y y y − = + = + − − = = −

2)利用模型进行循环计算获得SPACF 在其它各滞后期的值,即 a。-∑d.vp- 功k= 1-2a.1P
2)利用模型进行循环计算获得SPACF 在其它各滞后期的值,即 1 1, 1 1 1, 1 ˆ ˆ ˆ ˆ ˆ 1 ˆ k k k j k j j kk k k j j j − − − = − − = − = −
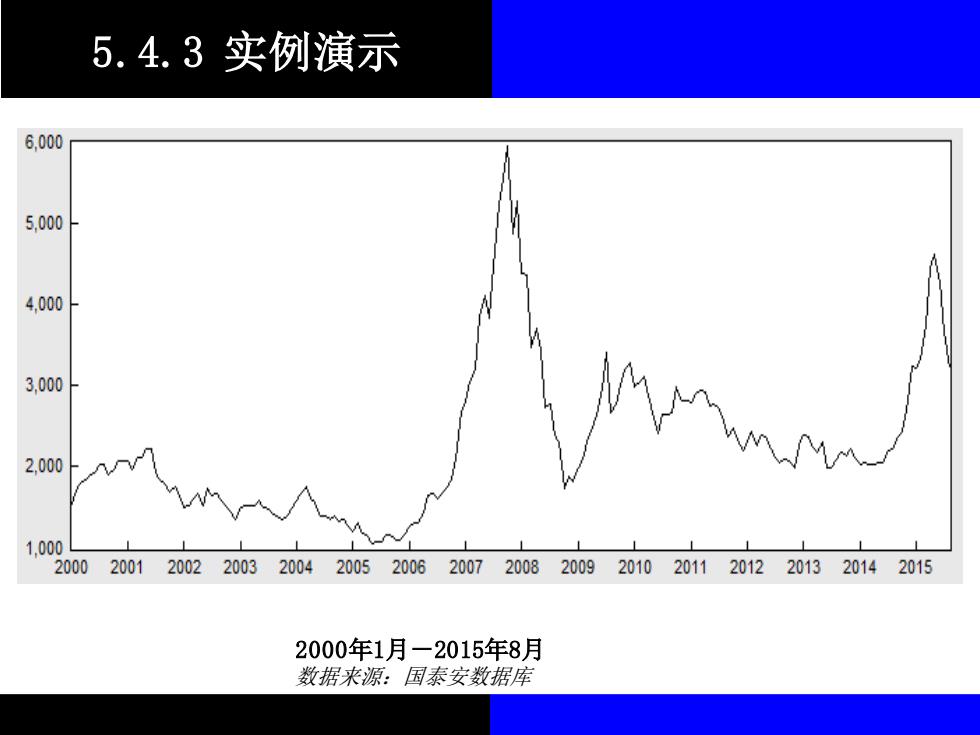
5.4.3实例演示 6,000 5,000 4,000 3,000 2,000 1,000 000200120022003200420052006200720082009201020112012201320142015 2000年1月-2015年8月 数据来源:国泰安数据库
5.4.3 实例演示 2000年1月-2015年8月 数据来源:国泰安数据库
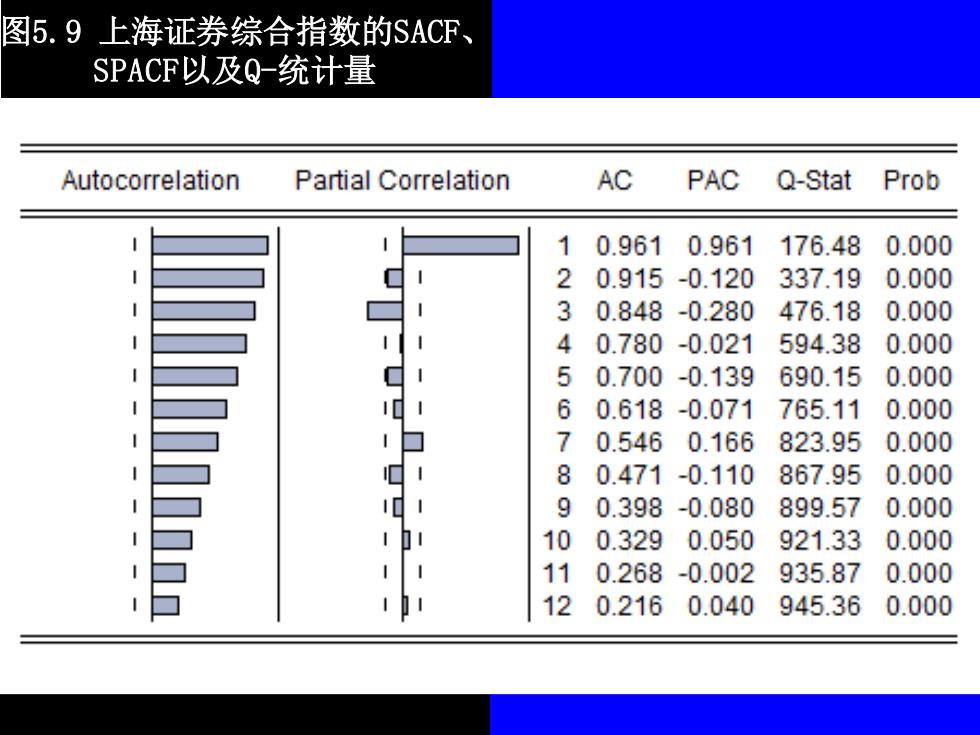
图5.9上海证券综合指数的SACP、 SPACF以及Q-统计量 Autocorrelation Partial Correlation AC PAC Q-Stat Prob 0.9610.961176.48 0.000 2 0.915-0.120 337.190.000 0.848-0.280 476.180.000 4 0.780-0.021594.380.000 50.700-0.139 690.150.000 01 60.618-0.071 765.110.000 1口 7 0.5460.166823.950.000 80.471-0.110 867.950.000 90.398 -0.080899.570.000 100.329 0.050 921.330.000 110.268-0.002 935.87 0.000 120.2160.040 945.360.000
图5.9 上海证券综合指数的SACF、 SPACF以及Q-统计量

图5.10上海证券综合指数的 SACF、SPACF以及Q-统计量 .3 g 2 .3 2000 200120022003200420052006200720082009201020112012201320142015
图5.10 上海证券综合指数的 SACF、SPACF以及Q-统计量
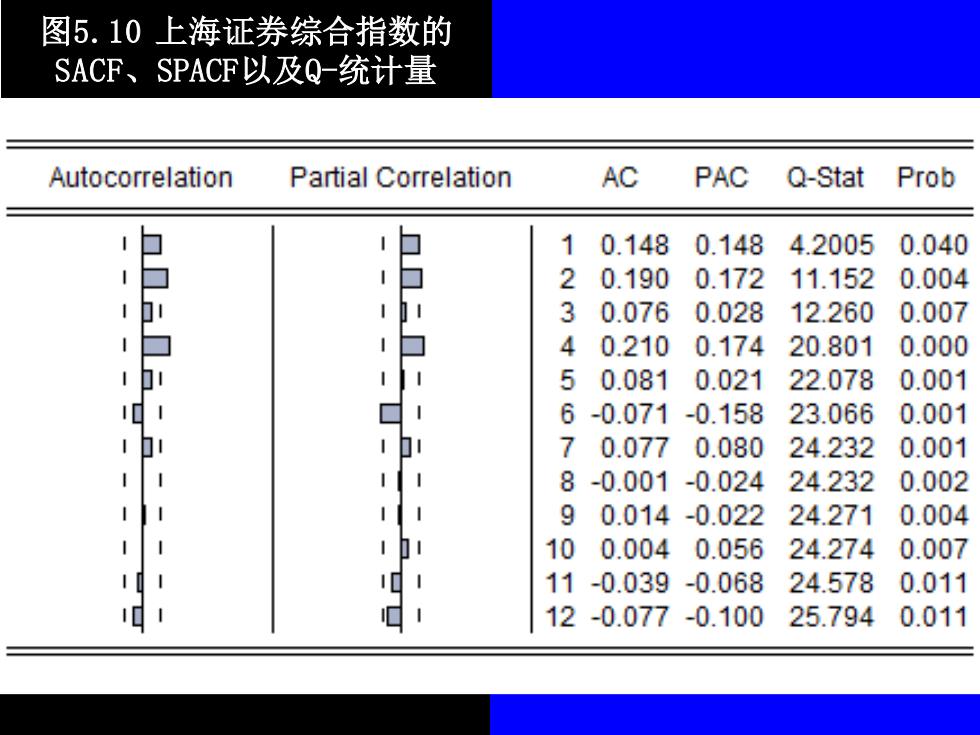
图5.10上海证券综合指数的 SACF、SPACF以及Q-统计量 Autocorrelation Partial Correlation AC PAC Q-Stat Prob 1 0.148 0.148 4.20050.040 2 0.190 0.172 11.1520.004 3 0.076 0.028 12.260 0.007 4 0.2100.17420.8010.000 5 0.0810.021 22.0780.001 01 6-0.071-0.158 23.0660.001 1b1 10 70.0770.080 24.2320.001 8-0.001-0.02424.232 0.002 90.014-0.02224.2710.004 100.0040.05624.2740.007 101 11-0.039-0.068 24.5780.011 12-0.077-0.10025.7940.011
图5.10 上海证券综合指数的 SACF、SPACF以及Q-统计量

5.5自相关性检验 5.5.1 Breusch-Godfrey LM序列相关 性检验 基本思路: 将原始回归模型写成一般形式: y=xB+u 其中:x,表示包括常数项在内的一组解 释变量
5.5 自相关性检验 5.5.1 Breusch-Godfrey LM 序列相关 性检验 基本思路: 将原始回归模型写成一般形式: 其中: 表示包括常数项在内的一组解 释变量。 t t t y x u = + t x

下面,就可以写出Breusch-Godfrey LM检验利用的辅助回归等式,即: y,=x,B*+441+2a,-2+L+中n,-m+8
下面,就可以写出 Breusch-Godfrey LM 检验利用的辅助回归等式,即: 1 1 2 2 ˆ ˆ ˆ t t t t m t m t y x u u u = + + + + + − − − L