
第三章 差分方程、滞后运算与 动态模型 3.1 一阶差分方程 3.2 动态乘数与脉冲响应函数 3.3 高阶差分方程 3.4滞后算子与滞后运算法
2 第三章 差分方程、滞后运算与 动态模型 3.1 一阶差分方程 3.2 动态乘数与脉冲响应函数 3.3 高阶差分方程 3.4 滞后算子与滞后运算法

3.1一阶差分方程 3.1.1差分方程的定义 y,=Cy-1+E, (3.1) 一个差分方程就是指将一个变量的 当期值定义为它的前一期和一个当期 的随机扰动因素的函数。模型(3.1) 等式的右侧只有因变量的一次滞后期 出现,这样的差分方程称为一阶差分 方程
3.1 一阶差分方程 3.1.1 差分方程的定义 (3.1) 一个差分方程就是指将一个变量的 当期值定义为它的前一期和一个当期 的随机扰动因素的函数。模型(3.1) 等式的右侧只有因变量的一次滞后期 出现,这样的差分方程称为一阶差分 方程。 3 t t t 1 y y = + −
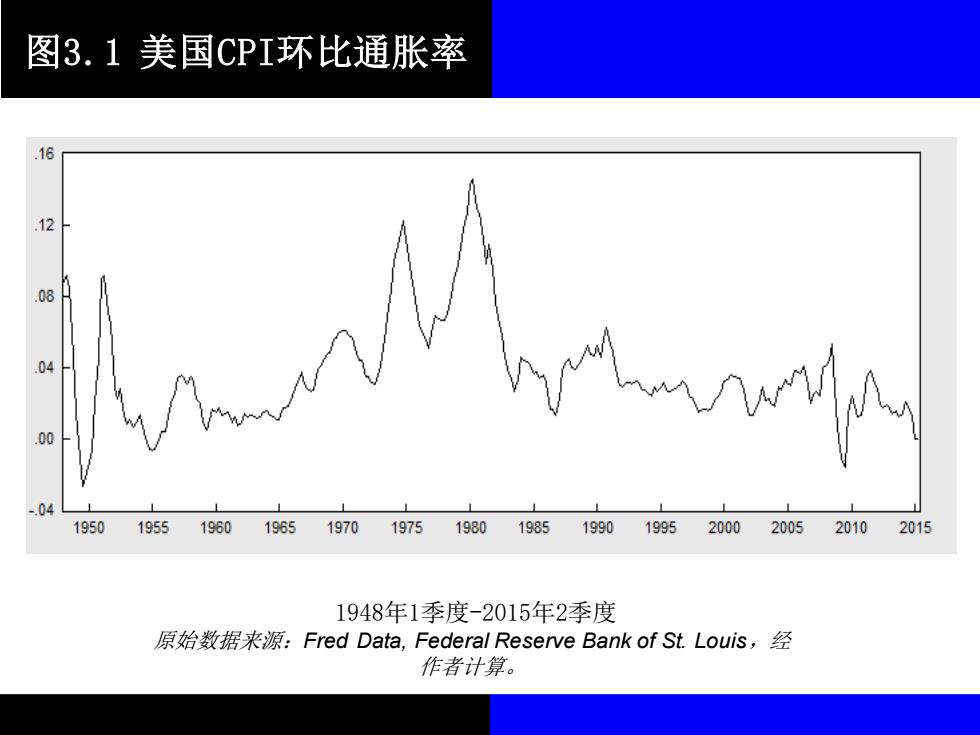
图3.1美国cPI环比通胀率 16 12 08 04 00 04 1950 195519601965197019751980198519901995200020052010 2015 1948年1季度-2015年2季度 原始数据来源:Fred Data,Federal Reserve Bank of St.Louis,经 作者计算
图3.1 美国CPI环比通胀率 1948年1季度-2015年2季度 原始数据来源:Fred Data, Federal Reserve Bank of St. Louis,经 作者计算

一些差分运算常用的表达式: y,-y-1=(C-l)y,-1+e △y=yt一yt-1 △(△y,)=△y,=(0y-y)-(0y-1--2)
5 1 1 ( 1) t t t t y y y − = − + − − t t t 1 y y y = − − 2 1 1 2 ( ) ( ) ( ) t t t t t t y y y y y y = = − − − − − − 一些差分运算常用的表达式:

3.1.2一阶差分方程的求解(反复迭代 法): 如果y,是给定的,则 y=ayo+8 y2=C1+82=a(0yo+E1)+82=a+a81+82 3=02+63=0'+0C8+aE2+E3 y,=0y1+6,=a'6+G,+a-2e2+…+6, -dy+>ao i=0 因此若给定初始值y,y,就可以由ε,的序列来表示
6 3.1.2 一阶差分方程的求解(反复迭代 法): 0 1 0 1 2 2 1 2 0 1 2 0 1 2 3 2 3 2 3 0 1 2 3 1 2 1 0 1 2 1 0 0 0 ( ) t t t t t t t t t i t i i t t y y y y y y y y y y y y y y y y − − − − − = = + = + = + + = + + = + = + + + = + = + + + + = + 如果 是给定的,则 因此若给定初始值 , 就可以由 的序列来表示

如果y,没有给定,则 yo=ay_1+8o=a(ay2+81)+80 =0y-2+081+E0 →=alym1+∑ac i=0 t+m →y,=ym1+∑a'e
7 0 0 1 0 2 1 0 2 2 1 0 1 0 1 0 1 1 0 ( ) m m j m j j t m t m i t m t i i y y y y y y y y y − − − − − + − − − = + + + − − − = = + = + + = + + = + = + 如果 没有给定,则

可以观察到, (1)如果a1,那么o+m+1的取值随 着m的不断增大将不会逐渐减小为0, 而是趋近于无穷大。此时y,称为非收 敛序列
可以观察到, (1)如果 ,那么 的取值随 着m的不断增大而减小,最终减为0, 此时 称为收敛序列。 (2)如果 ,那么 的取值随 着m的不断增大将不会逐渐减小为0, 而是趋近于无穷大。此时 称为非收 敛序列。 1 1 t m 1 + + t y 1 t m 1 + + t y

(3)如果a=1,差分方程描绘的变 量序列仍然是非收敛序列,但这种特 殊情况下的差分方程对应一个专门的 名称,叫做随机游走过程
(3)如果 ,差分方程描绘的变 量序列仍然是非收敛序列,但这种特 殊情况下的差分方程对应一个专门的 名称,叫做随机游走过程。 =1
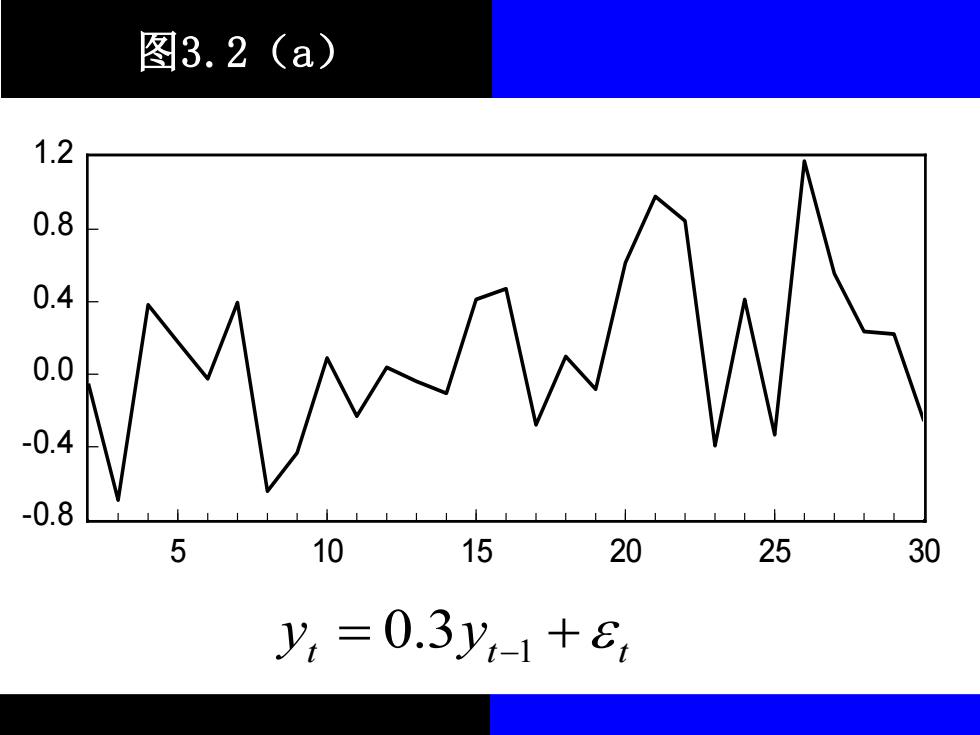
图3.2(a) 1.2 0.8 0.4 0.0 -0.4 -0.8 5 10 15 20 25 30 y,=0.3y,-1+6
图3.2(a) 经过以上分析,可以得出结论:一阶差分方 程中的一阶滞后项的系数的大小关键性地决定了 差分方程的求解结果。实际上,这个系数的取值 也关键性地决定了时间序列变量的动态走势特征。 后面的图即描绘了一阶差分方程中不同 系数的 所对应的 序列的动态路径。 t y -0.8 -0.4 0.0 0.4 0.8 1.2 5 10 15 20 25 30 t t t y = y + 3 −1 0

图3.2 (b) 1.0 0.5 y,=0.8y1+e 0.0 -0.5 -1.0 5 10 15 20 25 30
11 图3.2(b) -1.0 -0.5 0.0 0.5 1.0 5 10 15 20 25 30 1 0.8 t t t y y − = +