
4.3二阶自回归模型:AR(2) 4.3.1AR(2)过程的基本定义和性质 y,=C+0必y-1+02y-2+e iid(0,2)
4.3 二阶自回归模型:AR(2) 4.3.1 AR(2)过程的基本定义和性质 t t t t 1 1 2 2 y c y y = + + + − − 2 (0, ) t : iid

y=C+0Ly,-1+0x2Ly,-2+8, →(1-,L-x2L)y,=c+y,+E, 与滞后算子多项式(1-%,L-2L)对应 的特征方程(characteristic equation)为 22-a12-2=0 定理: 如果特征方程所有根2都落在单位圆内, 则AR(2)过程为平稳过程
1 1 2 2 1 2 1 2 2 1 2 (1 ) 1 0 t t t t t t t y c Ly Ly L L y c y L L AR = + + + − − − − = + + − − − − = 与滞后算子多项式( )对应 的特征方程(characteristic equation)为 定理: 如果特征方程所有根 都落在单位圆内, 则 (2)过程为平稳过程

利用滞后算子,可得 0(L)y,=C+E? 因此, y,=w(L)[c+8,] 其中, w(L)=(L)尸=W。+4L+w2L2+L
1 2 0 1 2 ( ) , ( )[ ] ( ) , ) ( t t t t L y c y L c L L L L − = + = + = = + + + 因此, 其 利用滞 中, 后算子 可得 L

因为滞后算子的特性Lc=c,所以 C w(L)c= 1-01-02 最终我们可以把AR(2)模型写成 y,是随机扰动项的函数,即: C y: +Ψo8,+Ψ18-1+Ψ28,-1+L 1-01-02
1 2 0 1 1 2 1 1 2 ( ) 1 AR 1 t t t t t Lc c c L c c y y − − = = − − = + + + + − − 因为滞后算子的特性 ,所以 最终我们可以把 (2)模型写成 是随机扰动项的函数,即: L

4.3.2AR(2)过程的均值 C 1-01-02
4.3.2 AR(2)过程的均值 1 1 2 c = − −

4.3.3AR(2)的方差、自协方差与自相关函数 由 y=C+C必1y-1+C2y-2+8, c=u(1-01-02) 可得 y,=I(1-01-02)+C%1y,-1+C2y-2+8
4.3.3 AR(2)的方差、自协方差与自相关函数 1 1 2 2 1 2 1 2 1 1 2 2 (1 ) (1 ) t t t t t t t t y c y y c y y y − − − − = + + + = − − = − − + + + 由 可得

并进而整理得 y,-u=(y,-1-4)+02(y,-2-4)+E, 两侧同乘以y,-4,然后取期望,得 Y)=01Yj-1+02Yj-2 根据自相关函数的定义,得关系式 P,=O1Pi-1+02Pj-2
1 1 2 2 1 1 2 2 1 1 2 2 ( ) ( ) , t t t t t j j j j j j j y y y y − − − − − − − − = − + − + − = + = + 并进而整理得 两侧同乘以 然后取期望,得 根据自相关函数的定义,得关系式

因此, p=a1po+a2p P2=ap+a2Po 又因为自相关函数具有以下性质 P=P’P=0=1 可得自相关函数在前2期的解析表达式 1-02 a-a3+&2 P2= 1-02
因此, 又因为自相关函数具有以下性质 可得自相关函数在前2期的解析表达式 1 1 0 2 1 2 1 1 2 0 = + − = + 0 0 0 1 j j = = = − , 1 1 2 2 2 1 2 2 2 2 1 1 = − − + = −

进而可推导出平稳AR(2)模型的 方差解析表达式: (1-a2) (1+a2)[(1-o2)-02]
进而可推导出平稳AR(2)模型的 方差解析表达式: 2 2 0 2 2 2 2 1 (1 ) (1 )[(1 ) ] − = + − −
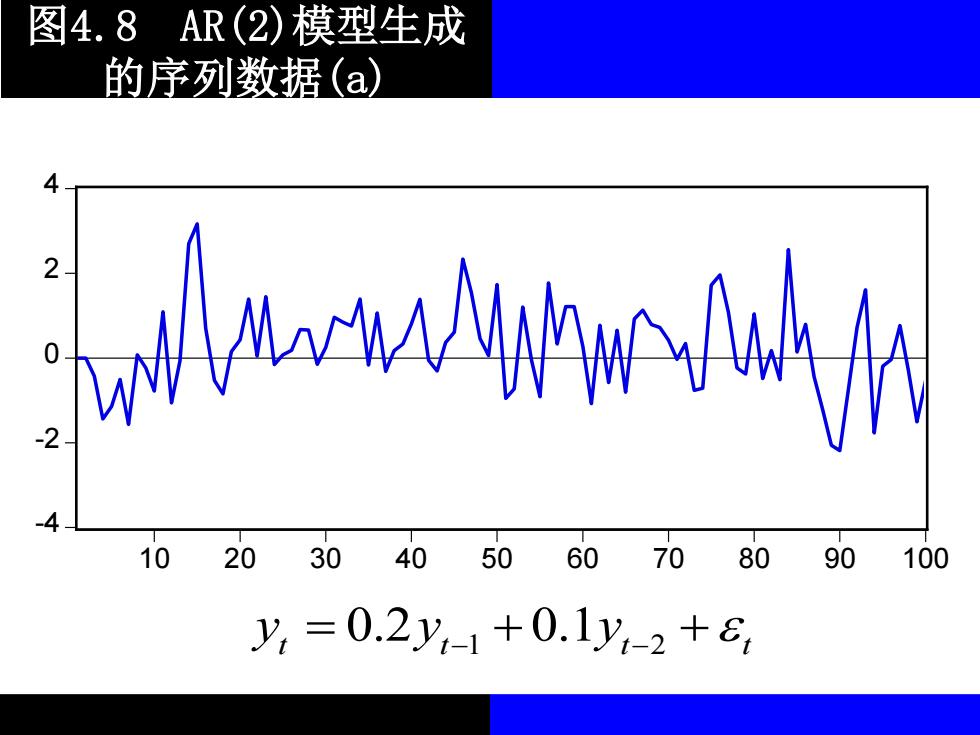
图4.8AR(2)模型生成 的序列数据(a) 44N山的 102030 4050 6070 8090100 y,=0.2y,-1+0.1y,-2+e
图4.8 AR(2)模型生成 的序列数据(a) -4 -2 0 2 4 10 20 30 40 50 60 70 80 90 100 t t t t 0.2 0.1 1 2 y y y = + + − −