
9.3格兰杰因果关系 从计量经济学发展的历史来看,格 兰杰因果关系的概念要早于VAR模型 。 格兰杰因果关系检验经常被解释为 在VAR模型中,某个变量是否可以用来提 高对其他相关变量的预测能力。所以, “格兰杰因果关系”的实质是一种“预 测”关系,而并非真正汉语意义上的 “因果关系
9.3 格兰杰因果关系 从计量经济学发展的历史来看,格 兰杰因果关系的概念要早于VAR模型。 格兰杰因果关系检验经常被解释为 在VAR模型中,某个变量是否可以用来提 高对其他相关变量的预测能力。所以, “格兰杰因果关系”的实质是一种“预 测”关系,而并非真正汉语意义上的 “因果关系

考虑一个简单的两个变量的VAR(p)模型 +L+ 例如,如果y2的系数都是0,y2,不是y的 格兰杰因果关系,即: H。:g=经=L=8=0 备择假设是这些系数中至少有一个不为0
(1) (1) (2) (2) 1 1 11 12 11 12 1, 1 1, 2 (1) (1) (2) (2) 2 2 21 22 21 22 2, 1 2, 2 ( ) ( ) 11 12 1, 2 1 ( ) ( ) 21 22 2, 2 2 VAR(p) : t t t t t t p p t t p p t y c y y y c y y y y − − − − − − = + + + + + 考虑一个简单的两个变量的 模型 L t 2, 2 1 (1) (2) ( ) 0 12 12 12 , 0, : : 0 t j t t p y y y H − = = = = 例如 如果 的系数都是 不是 的 格兰杰因果关系,即 备择假设是这些系数中至少有一个不为0。 L

如果原假设成立,则有: Yu eee +L+
如果原假设成立,则有: (1) (2) 1 1 11 11 1, 1 1, 2 (1) (1) (2) (2) 2 2 21 22 21 22 2, 1 2, 2 ( ) 11 1, 2 1 ( ) ( ) 21 22 2, 2 2 0 0 0 t t t t t t p t t p p t t y c y y y c y y y y − − − − − − = + + + + + L

LR检验:(T-(n2>h血 如果拒绝原假设,则称y,是y的格兰杰 因果关系。 与此不同, yu=C+ay+a2y2+L+apy-p +By21+B2y2-2+L+Bpyzrp+ H:B=B2=L=B。=0
LR : 检验 2 1 1 1 1 1, 1 2 1, 2 1, 1 2, 1 2 2, 2 2, - 1 0 1 2 : 0 t t t t t p t p t t p t p t p y y y C y y y y y y H − − − − − = + + + + + + + + + = = = = 如果拒绝原假设,则称 是 的格兰杰 因果关系。 与此不同, L L L

在VAR的相关内容中,与格兰杰因 果关系一个相关的概念就是所谓的 block exogeneity检验,翻译过来可以 称为“区块外生性”或“一揽子”外生 性检验。在选择VAR模型中是否要包含 额外的变量时,经常使用block exogeneity检验
在VAR的相关内容中,与格兰杰因 果关系一个相关的概念就是所谓的 block exogeneity检验,翻译过来可以 称为“区块外生性”或“一揽子”外生 性检验。在选择VAR模型中是否要包含 额外的变量时,经常使用block exogeneity检验
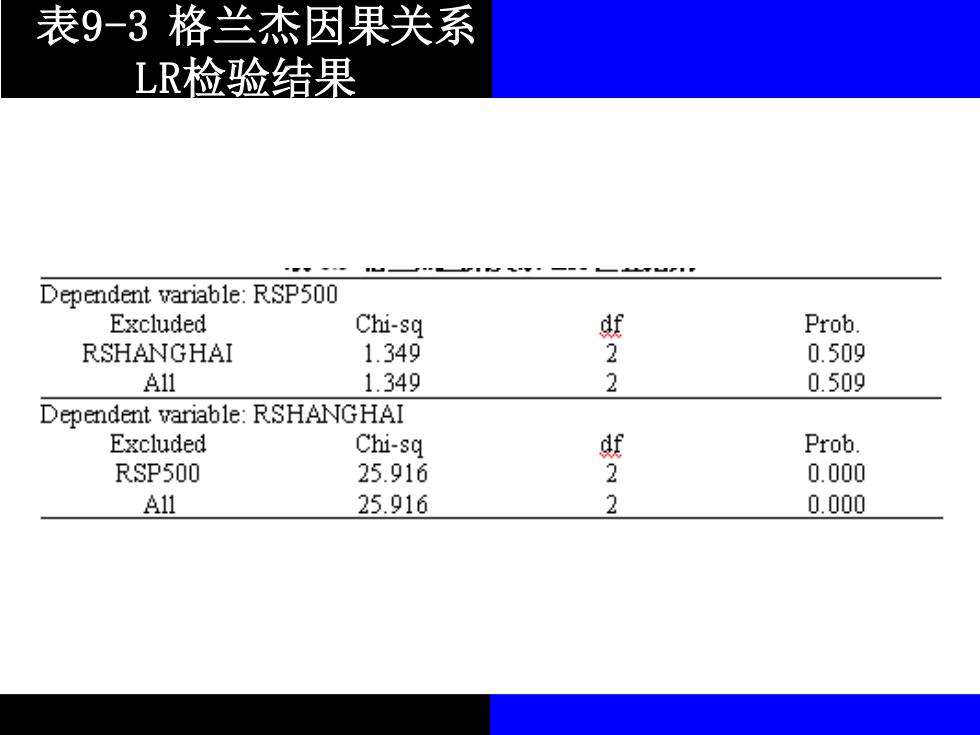
表9-3格兰杰因果关系 LR检验结果 Dependent variable:RSP500 Excluded Chi-sq Prob. RSHANGHAI 1.349 2 0.509 A11 1.349 2 0.509 Dependent variable:RSHANGHAI Excluded Chi-sq df Prob. RSP500 25.916 0.000 A11 25.916 2 0.000
表9-3 格兰杰因果关系 LR检验结果
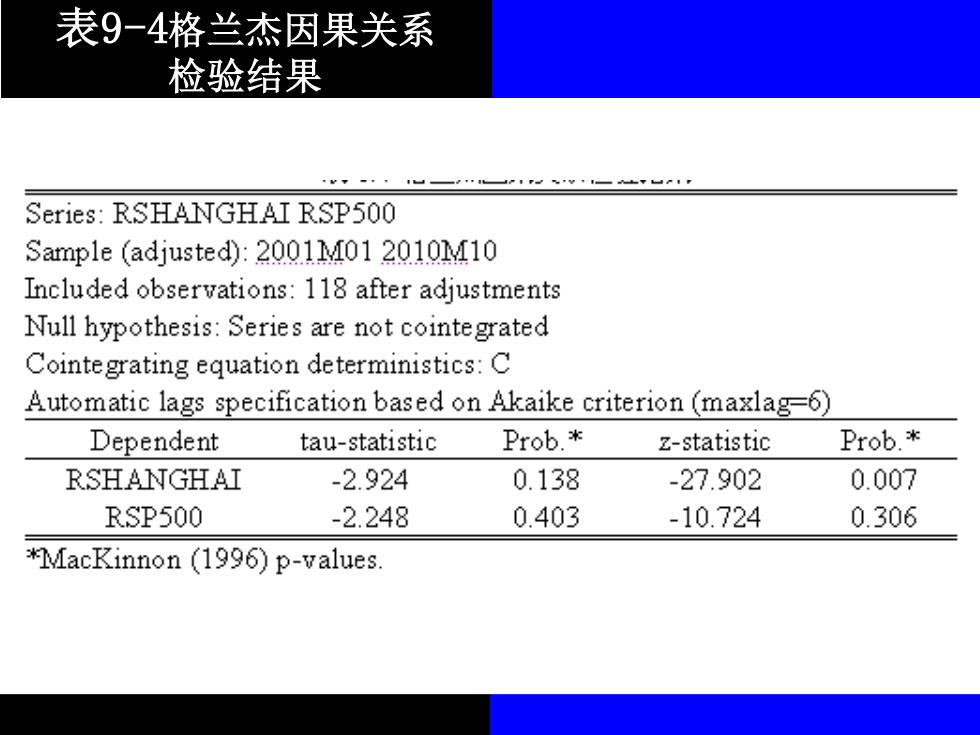
表9-4格兰杰因果关系 检验结果 Series:RSHANGHAI RSP500 Sample (adjusted):2001M01 2010M10 Included observations:118 after adjustments Null hypothesis:Series are not cointegrated Cointegrating equation deterministics:C Automatic lags specification based on Akaike criterion(maxlag-6) Dependent tau-statistic Prob. z-statistic Prob.* RSHANGHAI -2.924 0.138 -27.902 0.007 RSP500 -2.248 0.403 -10.724 0.306 *MacKinnon (1996)p-values
表9-4格兰杰因果关系 检验结果

9.4 向量自回归模型与脉冲响应分析 9.4.1VAR模型中的脉冲响应介绍 在很多情况下,VAR模型中的各个等 式中的系数并不是研究者关注的对象, 其主要原因就是VAR模型系统中的系数往 往非常多。 经济学家和计量经济学者经常使用 脉冲响应函数来解释VAR模型的经济学上 的含义
9.4 向量自回归模型与脉冲响应分析 9.4.1 VAR模型中的脉冲响应介绍 在很多情况下,VAR模型中的各个等 式中的系数并不是研究者关注的对象, 其主要原因就是VAR模型系统中的系数往 往非常多。 经济学家和计量经济学者经常使用 脉冲响应函数来解释VAR模型的经济学上 的含义
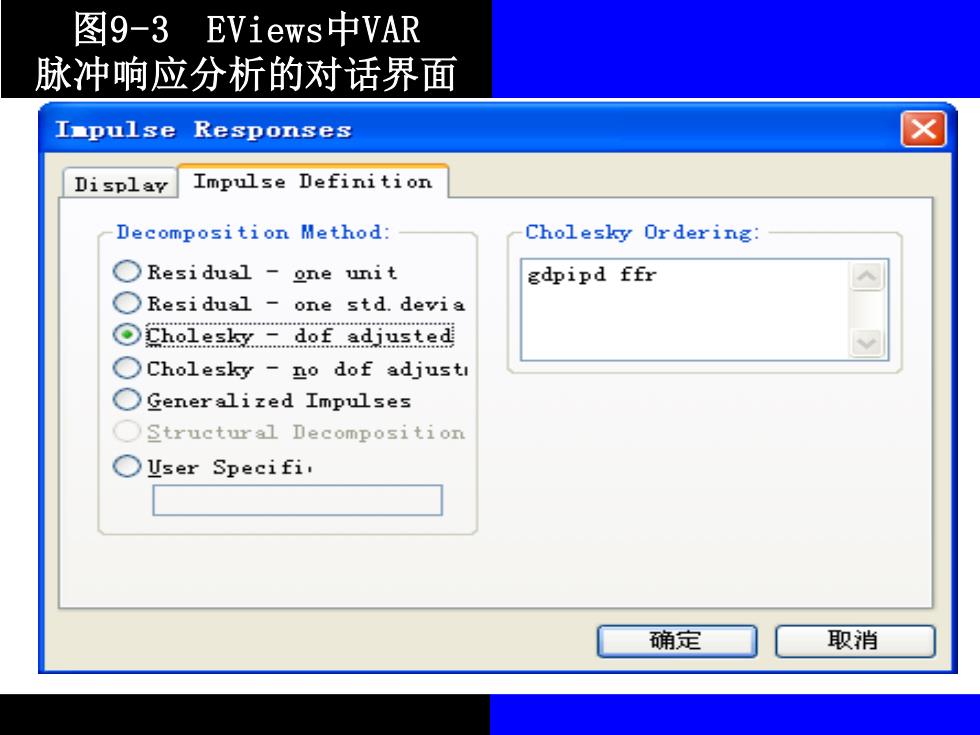
图9-3 EViews中VAR 脉冲响应分析的对话界面 I■pulse Responses Display Impulse Definition Decomposition Method: Cholesky Ordering: ○Residual-one unit gdpipd ffr OResidual-one std.devia ⊙Co1 esky_dof adjusted OCholesky -no dof adjust O Generalized Impulses OStructural Decomposition ○User Specifi, 确定 取消
图9-3 EViews中VAR 脉冲响应分析的对话界面

9.4.2简单脉冲响应函数 这里介绍的简单IRF包括两种形式: 一是所谓的“单位残差IRF”;另一个 是“单位标准差IRF
9.4.2 简单脉冲响应函数 这里介绍的简单IRF包括两种形式: 一是所谓的“单位残差IRF”;另一个 是“单位标准差IRF”