
12.4 非对称GARCH模型 12.4.1 非对称GARCH模型的背景介绍 由于在GARCHZ模型的方差等式 y=xφ+4,u,~N(0,0) i-a.+ai+ 中(u,)2=(-4,)》2=4,条件方差σ,很可能无法 区分正的和负的冲击可能造成的不同影 响
12.4 非对称GARCH模型 12.4.1 非对称GARCH模型的背景介绍 由于在GARCH模型的方差等式 中 ,条件方差 很可能无法 区分正的和负的冲击可能造成的不同影 响。 2 2 2 2 0 1 1 , (0, ) t t t t t p q t i t i j t i j y x u u N u − − = = = + = + + j 2 2 2 ( ) ( ) t t t u u u = − = 2 t

因此,利用GARCH模型分析金融资 产收益率的波动性问题,常常需要考 虑到这种非对称影响,而非对称GARCH 模型也就应运而生了。而这种非对称 性的反应有时称为杠杆效应。我们下 面分别介绍两种典型的非对称GARCHZ模 型,即TGARCH和EGARCHZ模型
因此,利用GARCH模型分析金融资 产收益率的波动性问题,常常需要考 虑到这种非对称影响,而非对称GARCH 模型也就应运而生了。而这种非对称 性的反应有时称为杠杆效应。我们下 面分别介绍两种典型的非对称GARCH模 型,即TGARCH和EGARCH模型

12.4.2门限GARCH模型 (TGARCH> 所谓TGARCH模型,即门限GARCH模型, 就是指利用虚设变量来设置一个门限用 以区分正的和负的冲击对条件波动性的 影响
12.4.2 门限GARCH模型(TGARCH) 所谓TGARCH模型,即门限GARCH模型, 就是指利用虚设变量来设置一个门限用 以区分正的和负的冲击对条件波动性的 影响

以GARCH(1,1)为例,要建立只有一个 门限的TGARCH模型,首先,设立一个虚设 变量,满足以下条件,即 1=0,4-1≥0 1,=1,41<0 (12.41) 然后,设立GARCH模型的方差与均值等式: y=X0+4,4,~N0,o) o=+44+4-+Bo2(12.42)
以GARCH(1,1)为例,要建立只有一个 门限的TGARCH模型,首先,设立一个虚设 变量,满足以下条件,即 (12.41) 然后,设立GARCH模型的方差与均值等式: (12.42) 1 1 1 1 0, 0 1, 0 t t t t I u I u − − − − = = 2 2 2 2 2 0 1 1 1 1 1 1 1 , (0, ) t t t t t t t t t t y x u u N u u I − − − − = + = + + +

如果将模型(12.42)中的方差等式 明确的表示出来,可以写成: o=4+441+B.o241≥0 (12.43) o=4+(C+)41+Ro24<0
如果将模型(12.42)中的方差等式 明确的表示出来,可以写成: (12.43) 2 2 2 0 1 1 1 1 1 2 2 2 0 1 1 1 1 1 1 , 0 ( ) , <0 t t t t t t t t u u u u − − − − − − = + + = + + +

如果a≠0,那么TGARCH模型捕捉 了一定的非对称性。当=0时, TGARCH模型就变回到一般的GARCH模型。 在一般GARCH模型中,只要a%+B<1, 就可以确保模型系统具有恒定的无条 件方差。而对于TGARCH模型,不难证 明,必须满足下列条件,才能确保模 型系统具有恒定的无条件方差,即: 01+B+0.50<1
如果 ,那么TGARCH模型捕捉 了一定的非对称性。当 时, TGARCH模型就变回到一般的GARCH模型。 在一般GARCH模型中,只要 , 就可以确保模型系统具有恒定的无条 件方差。而对于TGARCH模型,不难证 明,必须满足下列条件,才能确保模 型系统具有恒定的无条件方差,即: 。 1 0 1 = 0 1 1 + 1 1 1 1 + + 0.5 1

虽然以上讨论的内容是基于只有一 个门限的TGARCH(1,1)模型的,但可以 推广到含有多个门限的TGARCH(q,p)模 型,只要将模型(12.42)进行拓展,即: y,=x0+4,4,~N0,o) -a+ag+立8,+c(12.44 其中,代表门限个数。并且,如果 w<0,则L,=0;如果w,≥0,则I,=1
虽然以上讨论的内容是基于只有一 个门限的TGARCH(1,1)模型的,但可以 推广到含有多个门限的TGARCH(q,p)模 型,只要将模型(12.42)进行拓展,即: (12.44) 其中,r代表门限个数。并且,如果 ,则 ;如果 ,则 。 2 2 2 2 2 0 1 1 1 , (0, ) t t t t t p q r t i t i j t j k t k t k i j k y x u u N u u I − − − − = = = = + = + + + 0 t u 1 t 0 I = t 0 u t I =

表12-8金融资产收益率的 TGARCH(1,1)模型估计结果 A.标准普尔500股票收益率TGARCH模型估讦 Dependent Variable:SP500RETURN Method:ML-ARCH (Marquardt)-Normal distribution Included observations:13561 after adjustments Convergence achieved after 17 iterations Presample variance:backcast (parameter=0.7) GARCH=C(3)+C(4)*RESID(-1)2+C(5)*RESID(-1)2*(RESID(-1)<0)+ C(6)*GARCH(-1) Variable Coefficient Std.Error z-Statistic Prob. 0 0.000 0.000 4.099 0.000 SP500RETURN(-1) 0.111 0.009 12.16 0.000 Variance Equation 0.000 0.000 12.30 0.000 RESID(-1)02 0.022 0.003 6.977 0.000 RESID(-12*(RESID(- 0.102 24.35 0.000 1)<0 0.004 GARCH(-1) 0.922 0.003 366.6 0.000 R-squared -0.005 Mean dependent var 0.000 Adjusted R-squared -0.005 S.D.dependent var 0.010 S.E.ofregression 0.010 Akaike info criterion -6.824 Sum squared resid 1.346 Schwarz criterion -6.821 Log likelihood 46277 Hannan-Quinn criter -6.823 Durhin-Watson stat 2.146
表12-8 金融资产收益率的 TGARCH(1,1)模型估计结果

B.上海证券综合指数收益率TGARCH模型估计 Dependent Variable:SHANGHAIRETURN Method:ML-ARCH (Marquardt)-Normal distribution Included observations:2611 after adjustments Convergence achieved after 12 iterations Presample variance:backcast (parameter=0.7) GARCH=C(3)+C(4)*RESID(-1)2+C(5)*RESID(-1)2*(RESID(-1)<0)+ C(6)*GARCH(-1) Variable Coefficient Std.Error Z-Statistic Prob. C 0.000 0.000 0.987 0.324 SHANGHAIRETURN(-1) 0.027 0.020 1.353 0.176 Variance Equation C 0.000 0.000 6.512 0.000 RESID(-1)2 0.058 0.008 7.511 0.000 RESID(-1)2*(RESID(- 1)<0) 0.057 0.010 5.563 0.000 GARCH(-1) 0.904 0.007 135.9 0.000 R-squared -0.000 Mean dependent var 0.000 Adjusted R-squared -0.000 S.D.dependent var 0.017 S.E.ofregression 0.017 Akaike info criterion -5.526 Sum squared resid 0.766 Schwarz criterion -5.512 Log likelihood 7219.5 Hea如-Quinn criter. -5.521 Durbin-Watson stat 2.024
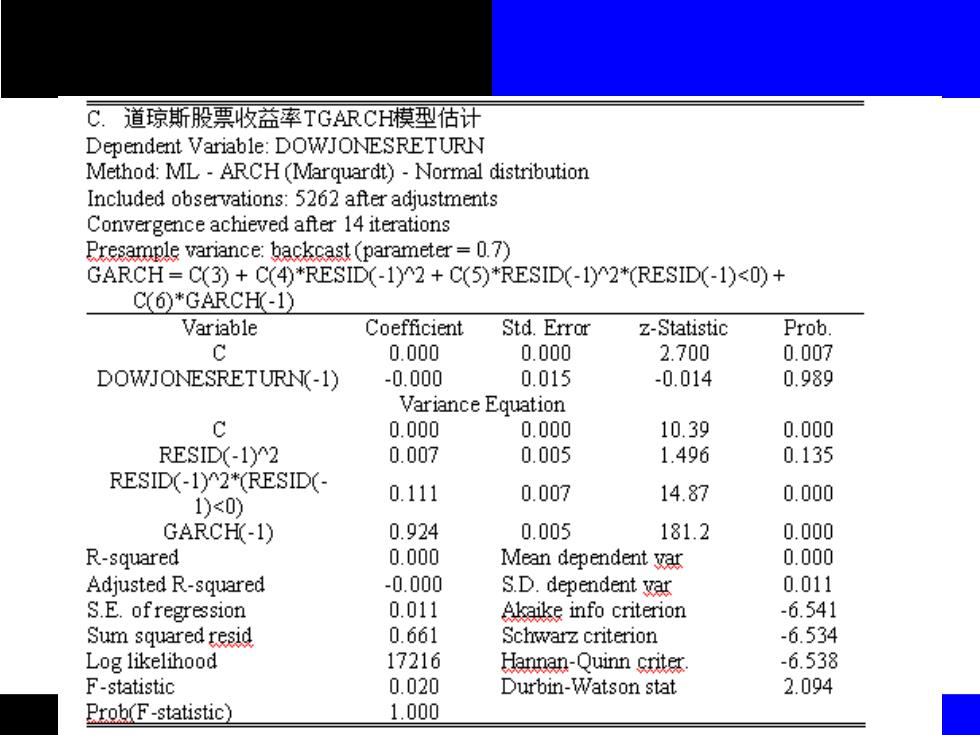
C.道琼斯股票收益率TGARCH模型估计 Dependent Variable:DOWJONESRETURN Method:ML-ARCH(Marquardt)-Normal distribution Included observations:5262 after adjustments Convergence achieved after 14 iterations Presample variance:backcast (parameter=0.7) GARCH=C(3)+C(4)*RESID(-1)2+C(5)*RESID(-1)2*(RESID(-1)<0)+ C(6)*GARCH(-1) Variable Coefficient Std.Error z-Statistic Prob. C 0.000 0.000 2.700 0.007 DOWJONESRETURN(-1) -0.000 0.015 -0.014 0.989 Variance Equation c 0.000 0.000 10.39 0.000 RESID(-1)2 0.007 0.005 1.496 0.135 RESID(-1)2*(RESID(- 0.111 0.007 1)<0) 14.87 0.000 GARCH(-1) 0.924 0.005 181.2 0.000 R-squared 0.000 Mean dependent var 0.000 Adjusted R-squared -0.000 S.D.dependent var 0.011 S.E.ofregression 0.011 Akaike info criterion -6.541 Sum squared resid 0.661 Schwarz criterion -6.534 Log likelihood 17216 Hannan-Quinn criter -6.538 F-statistic 0.020 Durbin-Watson stat 2.094 Broh(F-statistic】 1.000