
7.3去除趋势的方法 在实际应用当中,平稳时间序列 要比非平稳时间序列具有更多吸引人 的特性。另外,平稳时间序列与非平 稳时间序列在某些重要特性方面差异 明显
7.3 去除趋势的方法 在实际应用当中,平稳时间序列 要比非平稳时间序列具有更多吸引人 的特性。另外,平稳时间序列与非平 稳时间序列在某些重要特性方面差异 明显

但是,含有趋势的时间序列却永远 也不会回复到一个长期的固定水平。随 机扰动对含有趋势的时间序列的影响将 是长久的,表现出一种长期的记忆性
但是,含有趋势的时间序列却永远 也不会回复到一个长期的固定水平。随 机扰动对含有趋势的时间序列的影响将 是长久的,表现出一种长期的记忆性

如果含有趋势成分的非平稳时 间序列参与到计量回归中,许多经典 的回归估计假设条件将不再满足,所 以就必须小心解释相应的统计检验和 统计推断,有的情况下会出现所谓的 “伪回归”现象,而有的条件下需 要应用协整分析方法
如果含有趋势成分的非平稳时 间序列参与到计量回归中,许多经典 的回归估计假设条件将不再满足,所 以就必须小心解释相应的统计检验和 统计推断,有的情况下会出现所谓的 “伪回归” 现象,而有的条件下需 要应用协整分析方法

一般来说,常用的去除趋势的方 法有差分法和去除趋势法,前者主要针 对随机趋势非平稳时间序列,而后者主 要针对含有确定性趋势的非平稳时间序 列
一般来说,常用的去除趋势的方 法有差分法和去除趋势法,前者主要针 对随机趋势非平稳时间序列,而后者主 要针对含有确定性趋势的非平稳时间序 列

7.3.1差分法 差分法一般用来去除含有随机趋势的 非平稳时间序列。如果从AR模型的平稳性 条件来考虑,它非平稳,就是因为它的特 征方程的根含有一个单位根。所以也被称 为“单位根过程”,或者“一阶单整过 程”,记做I(1),其中“I”表示单整, “(1)”表示单整的阶数
7.3.1 差分法 差分法一般用来去除含有随机趋势的 非平稳时间序列。如果从AR模型的平稳性 条件来考虑,它非平稳,就是因为它的特 征方程的根含有一个单位根。所以也被称 为“单位根过程” ,或者“一阶单整过 程” ,记做I(1),其中“I”表示单整, “(1)”表示单整的阶数

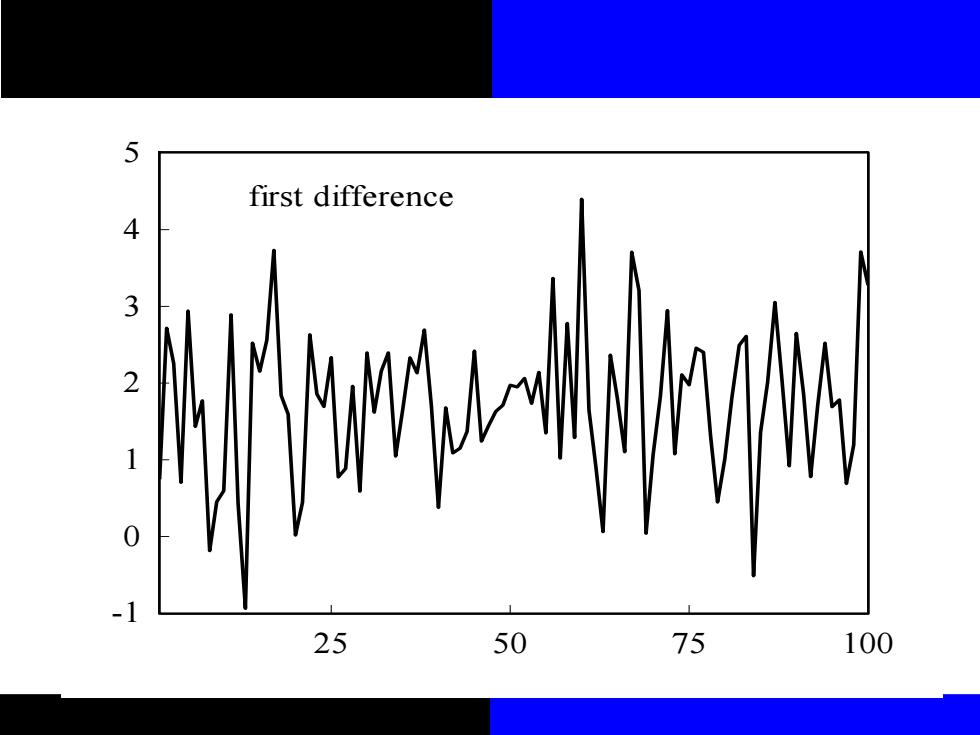
随机趋势非平稳过程可以通过差分 法变为平稳过程。如果是I(1),则一次 差分即可实现,而对于I(2)过程,则可 以通过两次差分获得平稳过程。 以随机游走过程为例,一阶差分就是 指使用原过程获得一次差分项△y,=y,-y 的表达式,其中“△”表示差分符号。所 以: △y,=Ei (7.22)
随机趋势非平稳过程可以通过差分 法变为平稳过程。如果是I(1),则一次 差分即可实现,而对于I(2)过程,则可 以通过两次差分获得平稳过程。 以随机游走过程为例,一阶差分就是 指使用原过程获得一次差分项 的表达式,其中“ ”表示差分符号。所 以: (7.22) t t t 1 y y y = − − = yt t

从模型(7.22)可以看出,基 于随机游走过程的一次差分△y,是一 个平稳的随机时序变量,因为£,等于 平稳白噪音过程
从模型(7.22)可以看出,基 于随机游走过程的一次差分 是一 个平稳的随机时序变量,因为 等于 平稳白噪音过程。 t y t
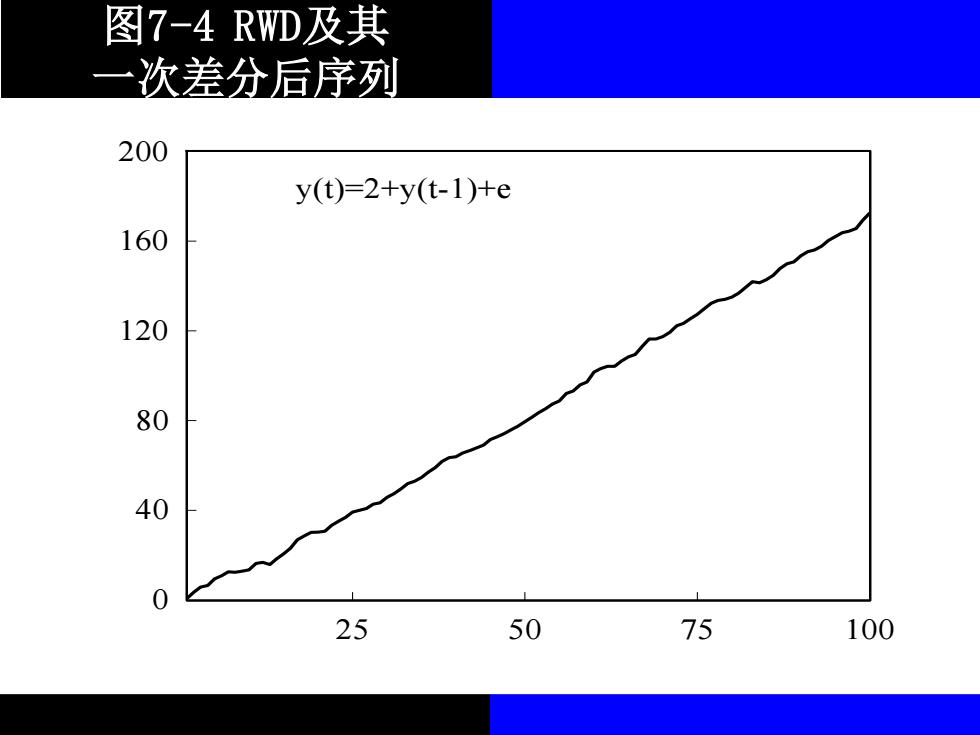
图7-4RWD及其 一次差分后序列 200 y(t)=2+y(t-1)+e 160 120 80 40 25 50 75 100
图7-4 RWD及其 一次差分后序列 0 4 0 8 0 120 160 200 2 5 5 0 7 5 100 y(t)=2+y(t-1)+e
5 first difference 4 25 50 75 100
-1 0 1 2 3 4 5 2 5 5 0 7 5 100 first difference

以上处理方法很容易拓展到高阶 单整序列。例如,假设y,是一个I(2) 过程,那么对其二次差分就可以获得 平稳序列,即: y=A(Ay,)=(0y,-y-i)-(y-y-2)=y,-y--y-2 其中:“A2”表示二次差分符号。 依此类推,“△3”表表示三次差分符 号,而“△””表示n次差分符号
以上处理方法很容易拓展到高阶 单整序列。例如,假设 是一个I(2) 过程,那么对其二次差分就可以获得 平稳序列,即: 其中:“ ”表示二次差分符号。 依此类推,“ ”表表示三次差分符 号,而“ ”表示n次差分符号。 t y 2 3 n 1 1 2 1 2 2 ( ) ( ) ( ) − − − − − = = − − − = − − t t t t t t t t t y y y y y y y y y