
13.3 门限模型 门限模型的核心不涉及概率转移矩 阵,而是根据设定的门限,来分析模型 在不同区制的变化。在门限模型中,区 制的变化可以体现在模型在两个不同状 态下的变化,也可以是平滑性的变化。 一般以自回归模型为研究对象,所以前 者对应的是门限自回归模型,而后者对 应的是平滑自回归模型
13.3 门限模型 门限模型的核心不涉及概率转移矩 阵,而是根据设定的门限,来分析模型 在不同区制的变化。在门限模型中,区 制的变化可以体现在模型在两个不同状 态下的变化,也可以是平滑性的变化。 一般以自回归模型为研究对象,所以前 者对应的是门限自回归模型,而后者对 应的是平滑自回归模型

13.3.1基本的门限模型 假设对于一个AR(1)模型,如果其 均值在某个时刻发生变化,这种情况就 是门限模型的一种。如图11-2所示,对 于一个样本为T的y,序列,在d时刻之前 均值为,而在d时刻后,其均值跳跃 到41
13.3.1 基本的门限模型 假设对于一个AR(1)模型,如果其 均值在某个时刻发生变化,这种情况就 是门限模型的一种。如图11-2所示,对 于一个样本为T的 序列,在d时刻之前 均值为 ,而在d时刻后,其均值跳跃 到 。 t y 0 1

这样我们可以把AR(1)模型写成: y,-4=4(y-1-4w)+6,S=0,1 更一般地,TAR模型可以写成如下形式: y=C+9以t+0p-p+,,=0,1
这样我们可以把AR(1)模型写成: 更一般地,TAR模型可以写成如下形式: 1 1 ( ) , 0,1 t st t st t t y y s − − = − + = , ,1 1 , 0,1 t t t t s s t s p t p t t y c y y s − − = + + + + =
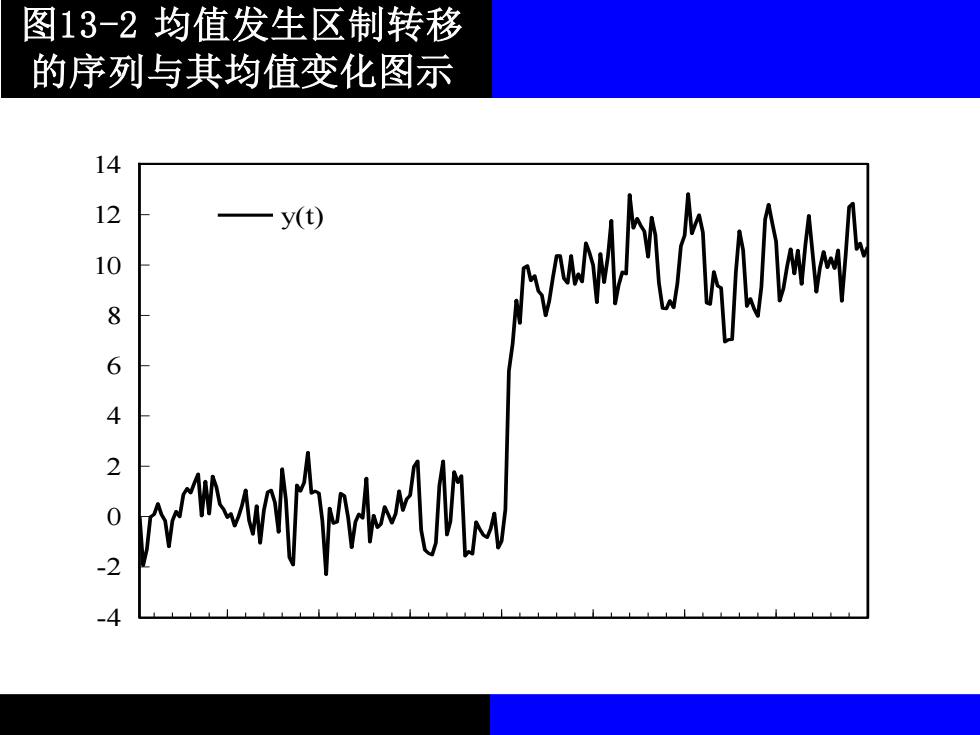
图13-2均值发生区制转移 的序列与其均值变化图示 14 12 y(t) 8 M wiwb
图13-2 均值发生区制转移 的序列与其均值变化图示 -4 -2 0 2 4 6 8 10 12 14 y(t)
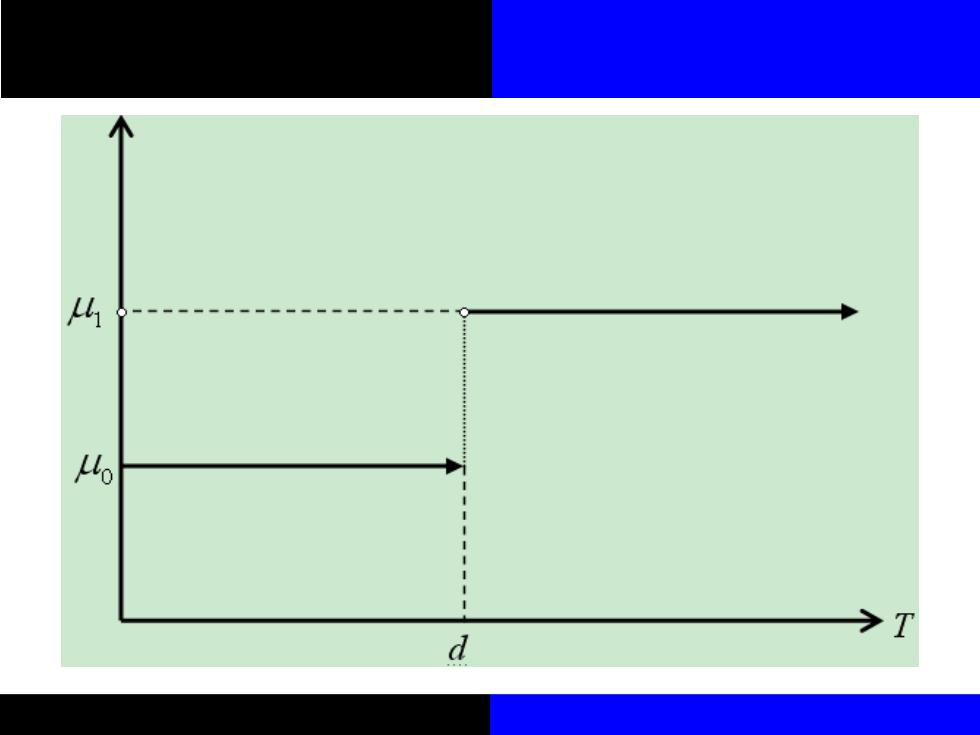
4 4 d

TAR模型与MS模型的设立不同,TAR 模型不涉及转移概率矩阵,而是利用一 个门限值,如δ,来区分不同的状态。 例如,假设存在一个分割点d,在T-d 之前和之后发生区制转变,那么: S,=0,yr-d4≤δ (9=1,y,-4>813.44)
TAR模型与MS模型的设立不同,TAR 模型不涉及转移概率矩阵,而是利用一 个门限值,如 ,来区分不同的状态。 例如,假设存在一个分割点d,在 之前和之后发生区制转变,那么: (13.44) T d − 0, 1, t T d t T d s y s y − − = =

现在,如果要估计模型(13.43), 我们需要确定门限值δ和分割点d是 否为已知的。如果这两个变量均为给 定的,那么就可以利用0LS分别对不同 区制内的模型进行回归估计。在估计 之后还可以利用传统的假设检验来检 验区制是否确实发生转变
现在,如果要估计模型(13.43), 我们需要确定门限值 和分割点d是 否为已知的。如果这两个变量均为给 定的,那么就可以利用OLS分别对不同 区制内的模型进行回归估计。在估计 之后还可以利用传统的假设检验来检 验区制是否确实发生转变。

例如,可以使用F检验,即: F= (SSRR-SSR)/r SSRU/T-k] 其中:SSR.和SSR分别表示有约束 条件和无约束条件下对应的残差平方 和,r表示约束条件的个数(如发生区 制变化的系数的个数),飞表示包括常 数项在内的自变量的个数
例如,可以使用F检验,即: 其中: 和 分别表示有约束 条件和无约束条件下对应的残差平方 和, 表示约束条件的个数(如发生区 制变化的系数的个数), 表示包括常 数项在内的自变量的个数。 ( ) R U U SSR SSR r F SSR T k − = − SSRR U SSR r k

注意,当d和6都未知或者其中有一个 未知时,由于干扰系数问题,待检验统计 量不再服从F分布,从而F检验不再适用。 例如,如果d已知,而δ未知,可以利用搜 索方法。如果这两个变量都未知,仍然可 以利用搜索方法获得。此时门限模型的 估计和检验,可以使用Andrews(1993)和 Andrews and Ploberger (1994)Sup Wald或者SupF检验进行
注意,当d和 都未知或者其中有一个 未知时,由于干扰系数问题,待检验统计 量不再服从F分布,从而F检验不再适用。 例如,如果d 已知,而 未知,可以利用搜 索方法。如果这两个变量都未知,仍然可 以利用搜索方法获得。此时门限模型的 估计和检验,可以使用Andrews (1993)和 Andrews and Ploberger (1994)的Sup Wald 或者Sup F检验进行。

13.3.2平滑转移自回归模型(STAR) STAR模型是TAR模型的一种拓展。在 TAR模型中,系数的变化被假定是突然性 的,而在STAR模型中,区制转移的过程 是缓慢、平滑的
13.3.2 平滑转移自回归模型(STAR) STAR模型是TAR模型的一种拓展。在 TAR模型中,系数的变化被假定是突然性 的,而在STAR模型中,区制转移的过程 是缓慢、平滑的