
第7章 非平稳金融时间序列模型 7.1 确定性趋势模型 7.2 随机性趋势模型 7.3 去除趋势的方法
2 第7章 非平稳金融时间序列模型 7.1 确定性趋势模型 7.2 随机性趋势模型 7.3 去除趋势的方法

7.1确定性趋势模型 所谓确定性趋势,是指模型 中含有明确的时间t变量,从而使 得某一时序变量随着时间而明确 地向上增长
7.1 确定性趋势模型 所谓确定性趋势,是指模型 中含有明确的时间t变量,从而使 得某一时序变量随着时间而明确 地向上增长

最简单的线性确定性趋势模型可以写成 y,=c+Bt+u,t=1,2, (7.1) 其中表示均值为0的平稳随机变量。 对(7.1)两边同取期望,可得 E(y)=c+Bt (7.2) (7.2)说明,只要系数不为0,则序列的 均值随时间推移而不断增大。正因为这个 特点,确定性趋势模型也称为“均值非平 稳”过程
► 最简单的线性确定性趋势模型可以写成 (7.1) 其中表示均值为0的平稳随机变量。 对(7.1)两边同取期望,可得 (7.2) (7.2)说明,只要系数不为0,则序列的 均值随时间推移而不断增大。正因为这个 特点,确定性趋势模型也称为“均值非平 稳”过程 t t y c t u = + + t =1,2,L ( ) E y c t t = +
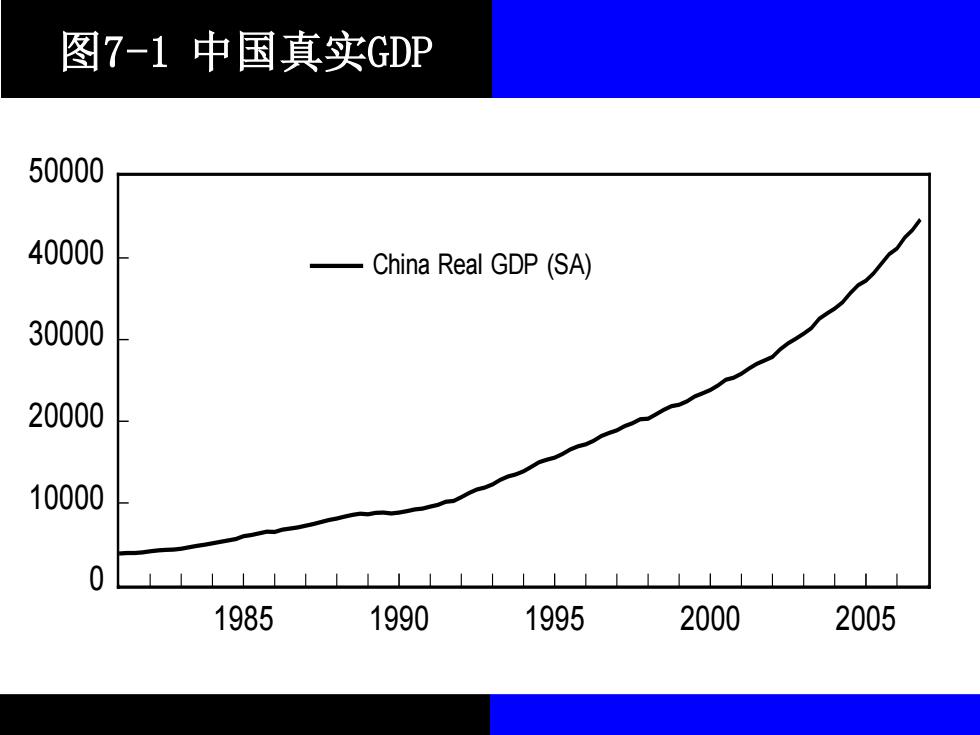
图7-1中国真实GDP 50000 40000 —China Real GDP(SA) 30000 20000 10000 0 1985 1990 1995 2000 2005
图7-1 中国真实GDP 0 10000 20000 30000 40000 50000 1985 1990 1995 2000 2005 China Real GDP (SA)

美国真实GDP 18.000 16,000 14,000 12,000 10,000 8,000 6,000 4,000 2,000 0 1950 1955196019651970197519801985199019952000200520102015 美国真实GDP时序数据:1947年1季度一2015年2季度
美国真实GDP 美国真实GDP时序数据:1947年1季度—2015年2季度

更一般地, y,=c+Bt+(L)u y,-E(y,)=0(L)u 其中:p(L)=Q,L+p,L+L+pL"是一个平稳的 滞后算子多项式
2 1 2 ( ) ( ) ( ) ( ) t t t t t m m y c t L u y E y L u L L L L = + + − = = + + + 更一般地, 其中: 是一个平稳的 滞后算子多项式。 L

7.2 随机性趋势模型 7.2.1随机趋势模型的基本定义 考虑AR(1)模型:y=y-1+E 其中,代表方差为o2的白噪音过程。 将模型写成:△y=E,· 如果假设初始观测值为yo,那么通 过反复迭代可以得到:y,=y。+∑c i1
7.2 随机性趋势模型 7.2.1 随机趋势模型的基本定义 考虑AR(1)模型: 其中 代表方差为 的白噪音过程。 将模型写成: 。 如果假设初始观测值为 ,那么通 过反复迭代可以得到: t t t 1 y y = + − t 2 t t = y 1 t t o i i y y = = + 0 y

这个表达式可以看成是一种随机 常数项,由于每个随机扰动因子对y 的条件均值的影响都是永久性的,所 以这样的模型经常被称为随机趋势模 型
这个表达式可以看成是一种随机 常数项,由于每个随机扰动因子对 的条件均值的影响都是永久性的,所 以这样的模型经常被称为随机趋势模 型。 t y

7.2.2 随机游走模型 实际上,模型(7.8)的形式就是一 个随机游走过程。那么随机游走过程的 特点有哪些呢?首先,从基本定义式可 以看到,随机游走过程就是一个常数项 为0并且自回归系数为1的AR(1)模型
7.2.2 随机游走模型 实际上,模型(7.8)的形式就是一 个随机游走过程。那么随机游走过程的 特点有哪些呢?首先,从基本定义式可 以看到,随机游走过程就是一个常数项 为0并且自回归系数为1的AR(1)模型

进一步考察随机过程的均值和方差: y,=y。+∑ i=l E0)=E0,+∑e)=% var(y.)=var(y,+6)-ta var0g,)=vVar0,+∑e,)=so2 i=l
进一步考察随机过程的均值和方差: 1 t t o i i y y = = + 0 1 ( ) ( ) t t o i i E y E y y = = + = 2 1 var( ) var( ) t t o i i y y t = = + = 2 1 var( ) var( ) s s o i i y y s = = + =