
第5章平稳金融时间序列:ARMA模型 5.1移动平均过程(MA Process) 5.2自回归移动平均过程(ARMA Processes) 5.3 部分自相关函数 (Partial Autocorrelations) 5.4 样本自相关与部分自相关函数 5.5 自相关性检验 5.6ARMA模型的实证分析及应用 5.7 实例应用:中国CPI通胀率的AR模型
第5章 平稳金融时间序列: ARMA模型 5.1 移动平均过程(MA Process) 5.2 自回归移动平均过程(ARMA Processes) 5.3 部分自相关函数 (Partial Autocorrelations) 5.4 样本自相关与部分自相关函数 5.5 自相关性检验 5.6 ARMA模型的实证分析及应用 5.7 实例应用:中国CPI通胀率的AR模型

5.1移动平均过程(MA Process) 5.1.1MA(1)模型 y,=C+e,+88-1 e:id(0,o2) 如果利用滞后算子来定义MA(1)过程, 则模型可以写作: y,=c+(1+8L)e
5.1 移动平均过程(MA Process) 5.1.1 MA(1) 模型 1 1 2 1 (0, ) MA (1 ) t t t t t t y c iid y c L 如果利用滞后算子来定义 (1)过程, 则模型可以写作: :
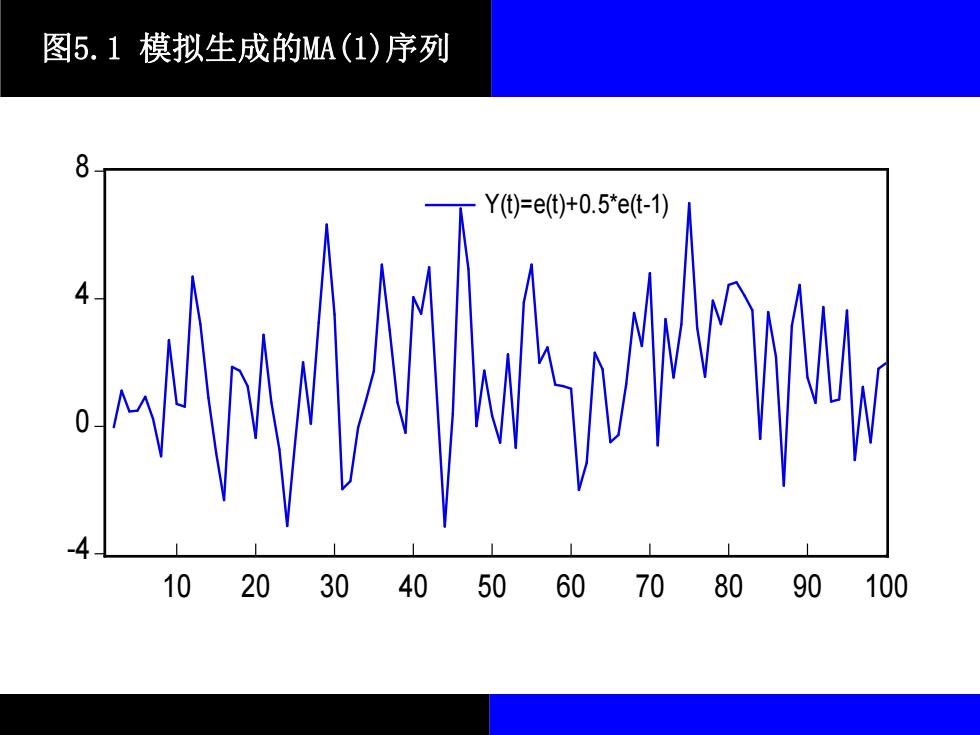
图5.1模拟生成的MA(1)序列 8 Yt)=et)+0.5*e(t-1) 10 2030405060708090100
图5.1 模拟生成的MA(1)序列 -4 0 4 8 10 20 30 40 50 60 70 80 90 100 Y(t)=e(t)+0.5*e(t-1)

均值 H=E(y,)=E(c+E,+8e,-1)=C 方差 =Ly-Ey)=E(e,+8e-)2=(1+e)o
均值 1 1 ( ) ( ) E t t t y E c c 方差 2 2 2 2 0 1 1 1 [ ( )] ( ) (1 ) E t t t t y E y E

自协方差 E(y-0yy-W=E(E,+88-e--H+8e--2) =E(e,e-j-1+8e,-e-+08-j-2+GE--j-2) 飞=4o,j ,j>1
自协方差 1 1 1 1 2 2 1 1 1 1 1 2 1 1 2 ( )( ) ( )( ) ( ) t t j t t t j t j t t j t t j t t j t t j E y y E E 2 1 1 = 0 1 j j j ,

自相关函数 j=1 j>1
自相关函数 1 21 0 , 1 (1 ) 0 , 1 j j jj

如果0换成它的倒到数形式行, 表 达式 o 是保持不变的。所以, 对于0取介于-0.5和0.5之间的实数, 可以产生完全相同的自相关函数图
如果 换成它的倒数形式 ,表 达式 是保持不变的。 所以, 对于 取介于-0.5和0.5之间的实数, 可以产生完全相同的自相关函数图。 1 1 1 1 2 1 (1 ) 1
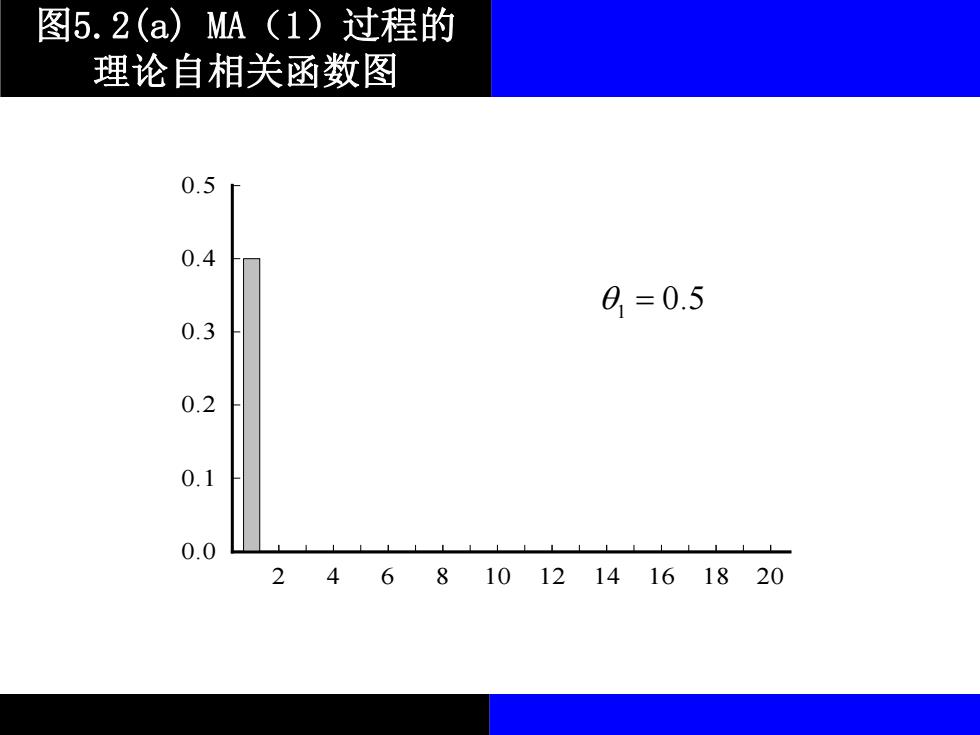
图5.2(a)MA(1)过程的 理论自相关函数图 0.5 0.4 0=0.5 0.3 0.2 0.1 0.0 2468101214161820
图5.2(a) MA(1)过程的 理论自相关函数图 0.0 0.1 0.2 0.3 0.4 0.5 2 4 6 8 10 12 14 16 18 20 1 0.5
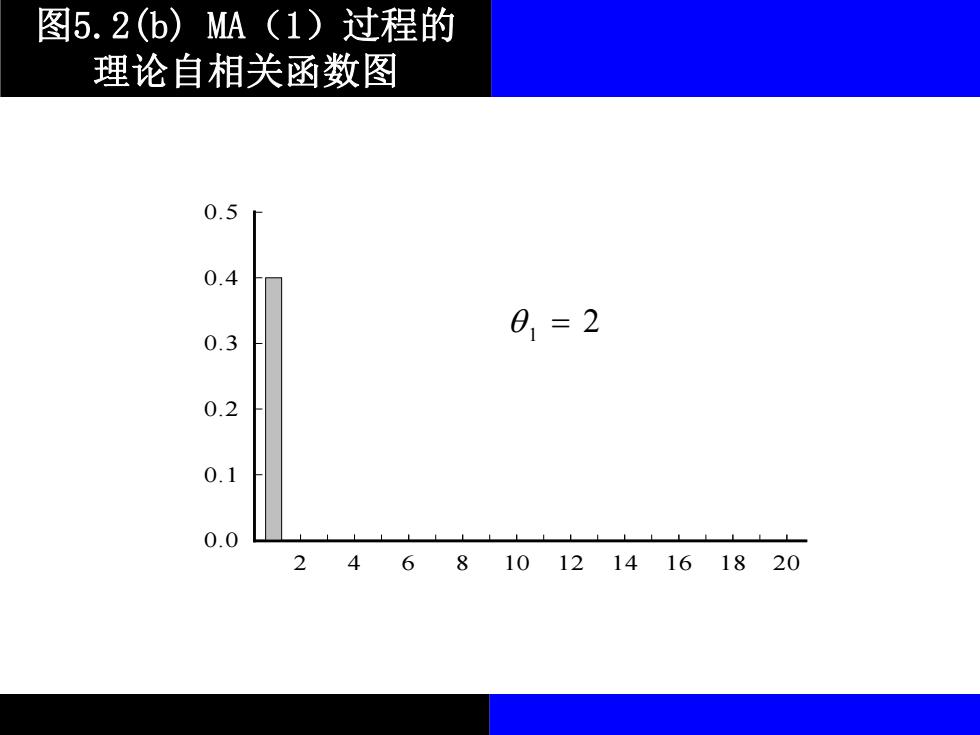
图5.2(b)MA(1)过程的 理论自相关函数图 0.5 0.4 01=2 0.3 0.2 0.1 0.0 2468101214161820
图5.2(b) MA(1)过程的 理论自相关函数图 0.0 0.1 0.2 0.3 0.4 0.5 2 4 6 8 10 12 14 16 18 20 1 2

图5.2(c)MA(1)过程的 理论自相关函数图 0.4 0.2 e=0.2 0.0 -0.2 -0.4 2468101214161820
图5.2(c) MA(1)过程的 理论自相关函数图 -0.4 -0.2 0.0 0.2 0.4 2 4 6 8 10 12 14 16 18 20 1 0.2