
第十二章金融计量中的条件异方差模型 12.1背景介绍 12.2 ARCH模型 12.3 GARCH模型 12.4 非对称GARCH模型 12.5 其他GARCH模型
第十二章 金融计量中的条件异方差模型 12.1 背景介绍 12.2 ARCH 模型 12.3 GARCH 模型 12.4 非对称GARCH 模型 12.5 其他GARCH 模型

12.1背景介绍 AR模型因为自身经常表现出较高的平 滑性而可以用来捕捉相对频率较低的时 间序列变量,如月度、季度通胀率、GDP 增长率等。对这样的时间序列数据其进 行AR模型回归之后的残差序列一般不表 现出很强的异方差性
12.1 背景介绍 AR模型因为自身经常表现出较高的平 滑性而可以用来捕捉相对频率较低的时 间序列变量,如月度、季度通胀率、GDP 增长率等。对这样的时间序列数据其进 行AR模型回归之后的残差序列一般不表 现出很强的异方差性
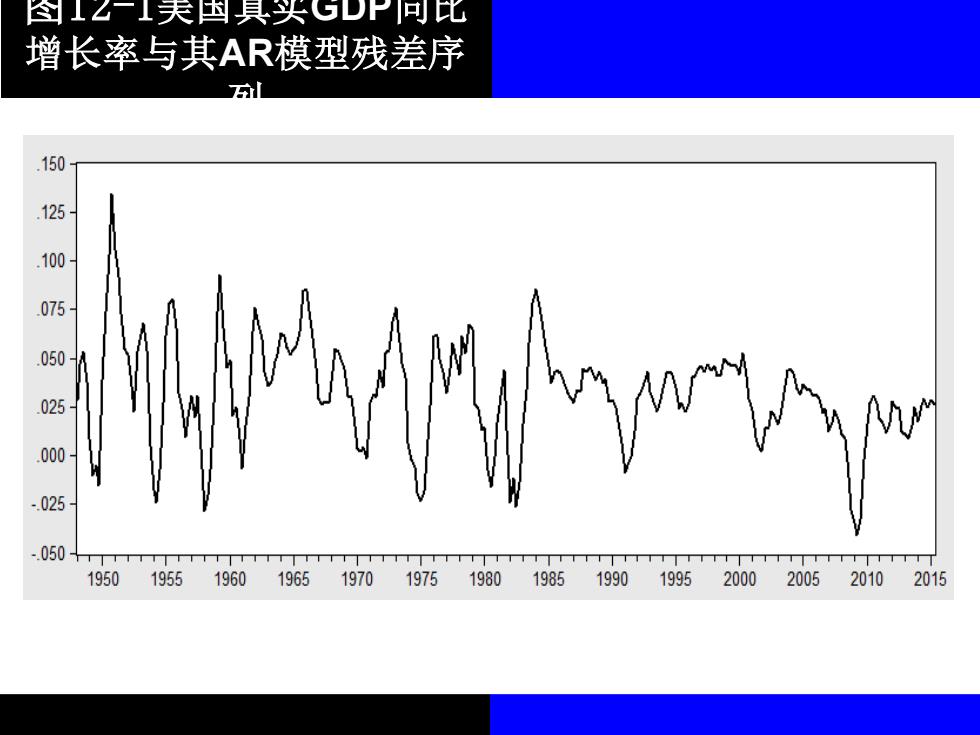
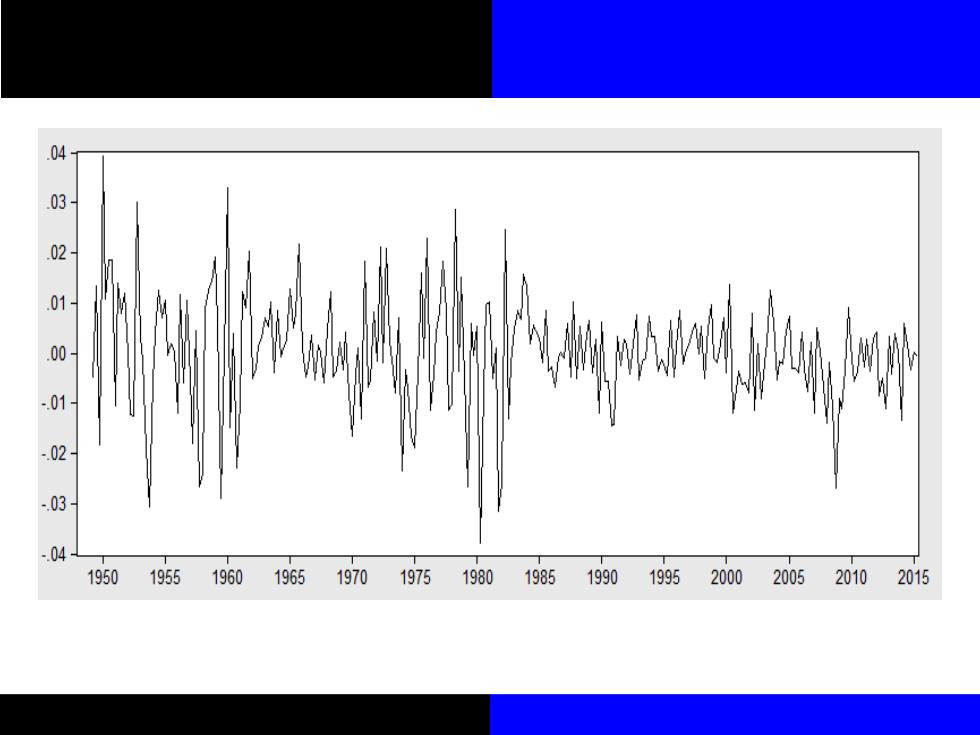
I☑一I天四具头P北 增长率与其AR模型残差序 150 125 100 075 050 025 000 pn 025 -050 TTT 1950 1955196019651970 19751980 19851990 19952000 200520102015
图12-1美国真实GDP同比 增长率与其AR模型残差序 列
04 03 .02 01 00 -01 -02 -粉o -03 -04 1950 1955196019651970197519801985199019952000200520102015
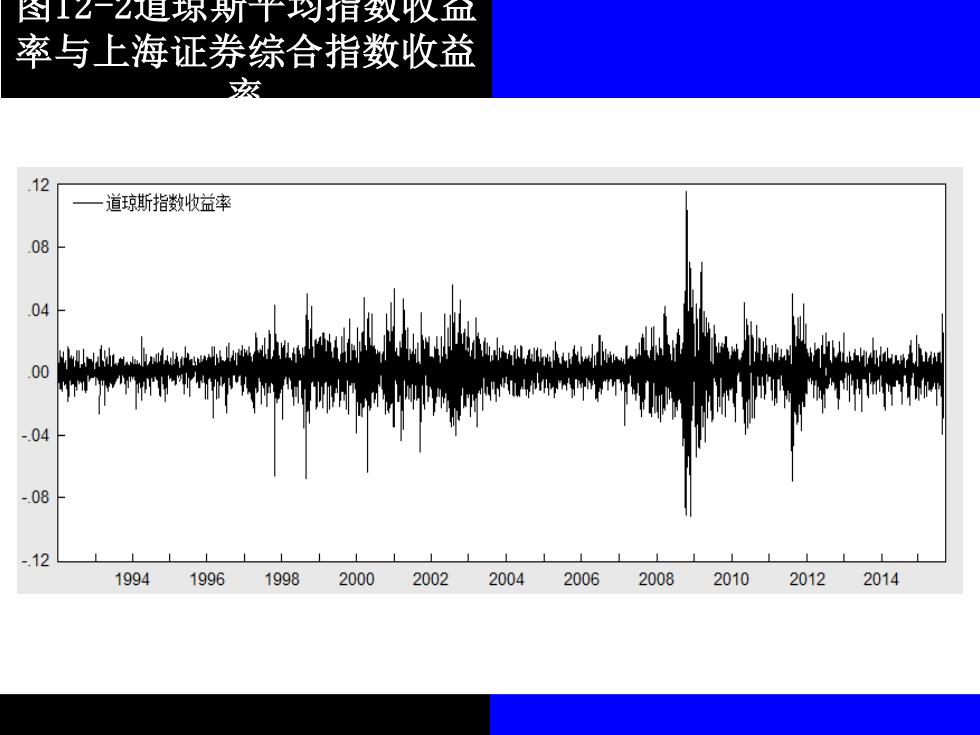
到1☑一目弥丹T中有双仪 率与上海证券综合指数收益 茨 .12 道琼斯指数收益率 08 04 % .04 m -08 -.12 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014
图12-2道琼斯平均指数收益 率与上海证券综合指数收益 率

.4 一上海证券综合指数收益率 .3 2 .1 .2 1996 1998 2000 2002 2004 2006 2008 2010 2012 2014
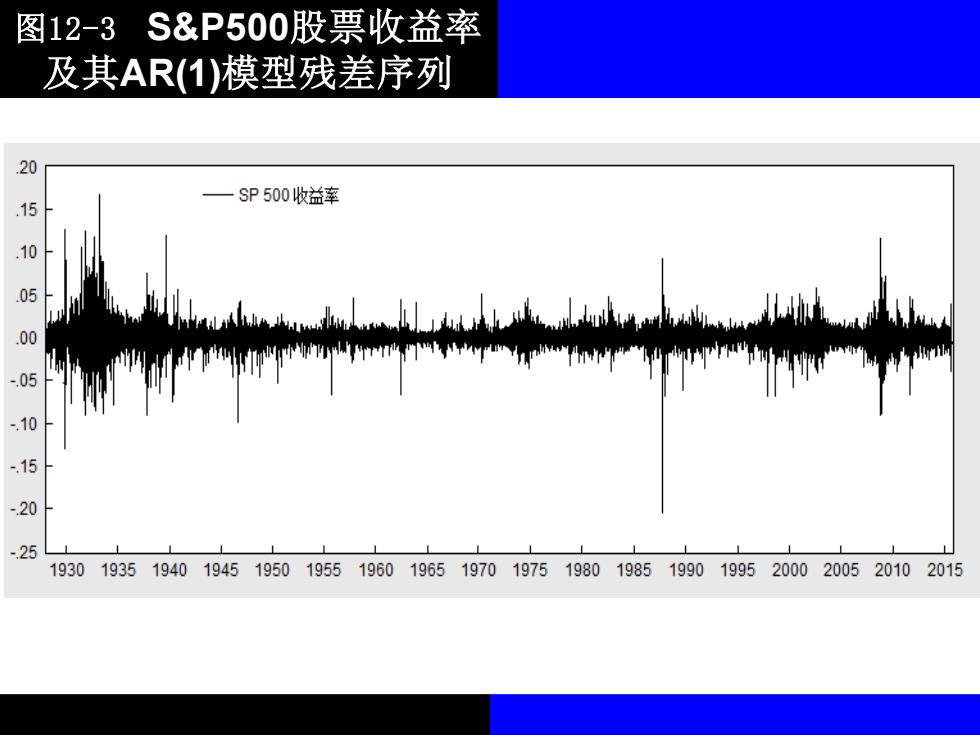
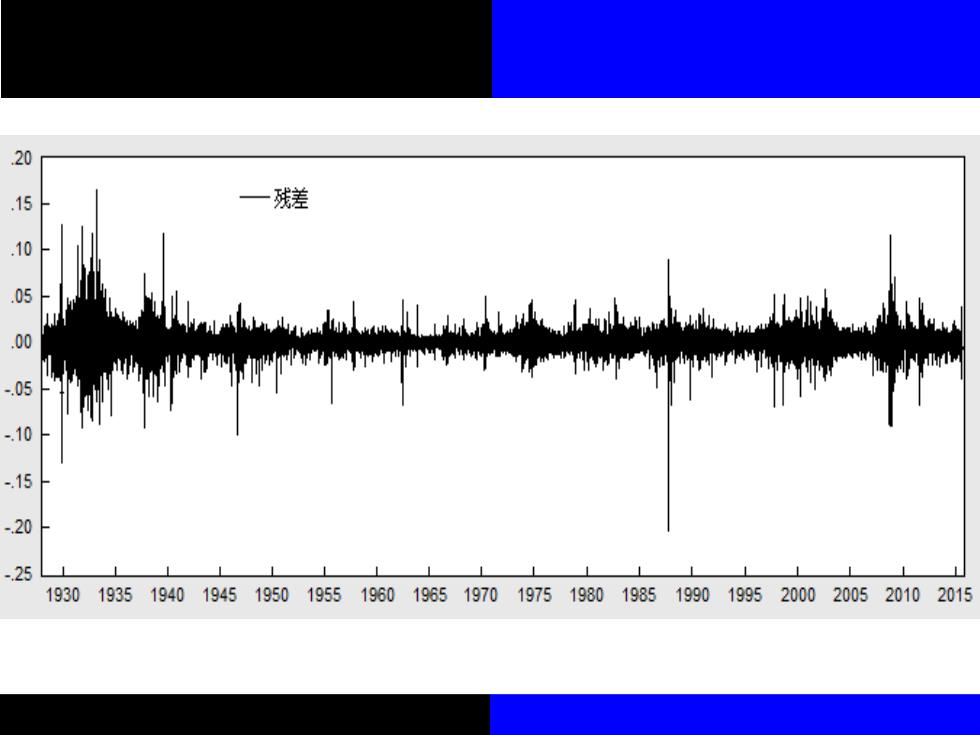
图12-3S&P500股票收益率 及其AR(1)模型残差序列 20 一SP500收益率 .10 .05 .00 -.05 -10 -15 -20 -25 193019351940194519501955196019651970197519801985199019952000200520102015
图12-3 S&P500股票收益率 及其AR(1)模型残差序列
15 一残差 05 Ld .00 .05 .10 -20 25 193019351940194519501955196019651970197519801985199019952000200520102015

12.2 ARCH模型 12.2.1ARCH模型的定义 ARCH模型的核心思想是,误差项在 时刻t的方差依赖于时刻t-1的误差平方 的大小。因此,在ARCH建模的过程中, 要涉及到两个核心的模型回归过程,即 原始的回归模型(常被称为条件均值回 归模型)和方差的回归模型(条件异方 差回归模型)
12.2 ARCH模型 12.2.1 ARCH模型的定义 ARCH模型的核心思想是,误差项在 时刻t的方差依赖于时刻t−1的误差平方 的大小。因此,在ARCH建模的过程中, 要涉及到两个核心的模型回归过程,即 原始的回归模型(常被称为条件均值回 归模型)和方差的回归模型(条件异方 差回归模型)

ARCH(1)模型的基本组成形式: 4=x0+4,4~N0,G) (12.1) o =E(u) (12.2) =0%+c44 其中:y,和x,分别表示因变量和自变量,4 表示无序列相关性的随机扰动项。σ表示 在t时刻随机扰动项的方差,因为方差随 时间变化,并且以过去的扰动项的信息 为变化条件,所以称为“条件异方差
ARCH(1)模型的基本组成形式: (12.1) (12.2) 其中: 和 分别表示因变量和自变量, 表示无序列相关性的随机扰动项。 表示 在t时刻随机扰动项的方差,因为方差随 时间变化,并且以过去的扰动项的信息 为变化条件,所以称为“条件异方差”。 t y t x t u 2 t