
、课程名称:概率论与数理统计 课程类别:学科专业必修课 适用专业:小学教育 考核方式:考试 总学时、学分:48学时、3学分 其中实验学时:0学时 一、课程教学目的 概率论与数理统计是小学教育专业(数学方向)的一门必修专业 主干课。概率论与数理统计是研究随机现象及其客观规律性的一门科 学。通过本课程的学习,让学生了解研究随机现象的数学思想与方法, 掌握概率论的基本知识、概念、公式及其应用,能熟练掌握数理统计 中的参数估计(点估计与区间估计)、假设检验、方差分析、卡方检 验等统计推断方法。 二、课程教学要求 帮助学生正确理解和掌握概率论中最基本的概念与原理,并引导 学生运用数理统计中的理论分析教育实践中的问题。具体来看,以下 几,点尤其值得关注: 1.注意本课程与前续课程的分工与衔接、以免遗漏或不必要的重 复。 2.注意小学教育(数学方向)学生的特点,注重课程中的基本概 念和基本理论的讲解,务必让学生明白各章最重要的概念和理论,同 时,主动放弃一些跟学生未来发展相关性较低的内容。 3.讲解数理统计中的推断统计方法时,一定要讲清各种统计方 法的应用条件和适用范围 三、先修课程 数学分析,高等代数
、课程名称:概率论与数理统计 课程类别:学科专业必修课 适用专业:小学教育 考核方式:考试 总学时、学分: 48 学时、3 学分 其中实验学时: 0 学时 一、课程教学目的 概率论与数理统计是小学教育专业(数学方向)的一门必修专业 主干课。概率论与数理统计是研究随机现象及其客观规律性的一门科 学。通过本课程的学习,让学生了解研究随机现象的数学思想与方法, 掌握概率论的基本知识、概念、公式及其应用,能熟练掌握数理统计 中的参数估计(点估计与区间估计)、假设检验、方差分析、卡方检 验等统计推断方法。 二、课程教学要求 帮助学生正确理解和掌握概率论中最基本的概念与原理,并引导 学生运用数理统计中的理论分析教育实践中的问题。具体来看,以下 几点尤其值得关注: 1.注意本课程与前续课程的分工与衔接、以免遗漏或不必要的重 复。 2.注意小学教育(数学方向)学生的特点,注重课程中的基本概 念和基本理论的讲解,务必让学生明白各章最重要的概念和理论,同 时,主动放弃一些跟学生未来发展相关性较低的内容。 3. 讲解数理统计中的推断统计方法时,一定要讲清各种统计方 法的应用条件和适用范围 三、先修课程 数学分析,高等代数

四、课程教学重、难点 重点:随机事件与概率,随机变量及其分布,参数估计(点估计 与区间估计)、假设检验、方差分析、卡方检验等统计推断方法。 难点:二维随机变量及其分布;抽样分布原理。 五、课程教学方法与教学手段 (1)学生先预习,教师讲授主要内容,讲练结合的教学方法。 (2)教学中拟采用灵活多样的授课方式:讲授式、启发式、讨 论式,激发学生对本课程的学习兴趣。 (3)注重问题的导入,尽量与实际问题相联系,使用计算机辅 助教学。 六、课程教学内容 第一章 随机事件与概率(6学时) 1.教学内容 (1)随机事件及其运算: (2)概率的定义及其确定方法: (3)概率的性质: (4)条件概率: (5)独立性。 2.重、难点提示 重点:概率的意义与定义、概率的基本性质、计算概率的基本公式、古典概型、几何概 型、贝努里概型: 难点:概率的意义、概率与频率的关系及概率模型的建立。 第二章随机变量及其分布(6学时) 1.教学内容 (1)随机变量及分布列:
四、课程教学重、难点 重点:随机事件与概率,随机变量及其分布,参数估计(点估计 与区间估计)、假设检验、方差分析、卡方检验等统计推断方法。 难点:二维随机变量及其分布;抽样分布原理。 五、课程教学方法与教学手段 (1)学生先预习,教师讲授主要内容,讲练结合的教学方法。 (2)教学中拟采用灵活多样的授课方式:讲授式、启发式、讨 论式,激发学生对本课程的学习兴趣。 (3)注重问题的导入,尽量与实际问题相联系,使用计算机辅 助教学。 六、课程教学内容 第一章 随机事件与概率(6 学时) 1.教学内容 (1)随机事件及其运算; (2)概率的定义及其确定方法; (3)概率的性质; (4)条件概率; (5)独立性。 2.重、难点提示 重点:概率的意义与定义、概率的基本性质、计算概率的基本公式、古典概型、几何概 型、贝努里概型; 难点:概率的意义、概率与频率的关系及概率模型的建立。 第二章 随机变量及其分布(6 学时) 1.教学内容 (1)随机变量及分布列;

(2)常用离散分布: (3)常用连续分布: 2.重、难点提示 重点:随机变量及其函数的分布: 难点:随机变量函数的分布。 第三章多维随机变量及其分布(4学时) 1.教学内容 (1)二维随机变量: (2)边缘分布: (3)条件分布: (4)相互独立的随机变量。 2.重、难点提示 重点:相互独立的随机变量: 难点:二维连续型随机变量的分布函数与密度函数的概念及它们的描述联合分布和边际 分布的概念及求法。 第四章 随机变量的数字特征(4学时) 1.教学内容 (1)数学期望: (2)方差: (3)协方差与相关系数: 2.重、难点提示 重点:常见分布的数学期望与方差: 难点:车贝晓夫定理的证明与应用。 第五章 概率分布与抽样理论(6学时) 1.教学内容 (1)抽样分布 (2)抽样分布理论 2.重、难点提示 重点:抽样分布理论
(2)常用离散分布; (3)常用连续分布; 2.重、难点提示 重点:随机变量及其函数的分布; 难点:随机变量函数的分布。 第三章 多维随机变量及其分布(4 学时) 1.教学内容 (1)二维随机变量; (2)边缘分布; (3)条件分布; (4)相互独立的随机变量。 2.重、难点提示 重点:相互独立的随机变量; 难点:二维连续型随机变量的分布函数与密度函数的概念及它们的描述联合分布和边际 分布的概念及求法。 第四章 随机变量的数字特征(4 学时) 1.教学内容 (1)数学期望; (2)方差; (3)协方差与相关系数; 2.重、难点提示 重点:常见分布的数学期望与方差; 难点:车贝晓夫定理的证明与应用。 第五章 概率分布与抽样理论(6 学时) 1.教学内容 (1)抽样分布 (2)抽样分布理论 2.重、难点提示 重点:抽样分布理论

难点:抽样分布理论中的内在逻辑。 第六章参数估计(4学时) 1.教学内容 (1)点估计与区间估计 (2)常见统计特征值的区间估计 2.重、难点提示 重点:区间估计的原理。 难点:方差之比的区间估计。 第七章假设检验(6学时) 1.教学内容 (1)假设检验的原理与方法 (2)假设检验的原理 (3)平均数的显著性检验 (4)平均数差异的显著性检验 (5)方差齐性检验。 2.重、难点提示 重点:假设检验的小概率原理:平均数差异的显著性检验。 难点:平均数差异的显著性检验。 第八章方差分析(6学时) 1.教学内容 (1)方差分析的原理与方法 (2)完全随机设计的方差分析方法 (3)随机区组设计的方差分析方法 2.重、难点提示 重点:方差分析的原理。 难点:随机区组设计的方差分析方法。 第九章卡方检验(6学时) 1.教学内容
难点:抽样分布理论中的内在逻辑。 第六章 参数估计(4 学时) 1.教学内容 (1)点估计与区间估计 (2)常见统计特征值的区间估计 2.重、难点提示 重点:区间估计的原理。 难点:方差之比的区间估计。 第七章 假设检验(6 学时) 1.教学内容 (1)假设检验的原理与方法 (2)假设检验的原理 (3)平均数的显著性检验 (4)平均数差异的显著性检验 (5)方差齐性检验。 2.重、难点提示 重点:假设检验的小概率原理;平均数差异的显著性检验。 难点:平均数差异的显著性检验。 第八章 方差分析(6 学时) 1.教学内容 (1)方差分析的原理与方法 (2)完全随机设计的方差分析方法 (3)随机区组设计的方差分析方法 2.重、难点提示 重点:方差分析的原理。 难点:随机区组设计的方差分析方法。 第九章 卡方检验(6 学时) 1.教学内容
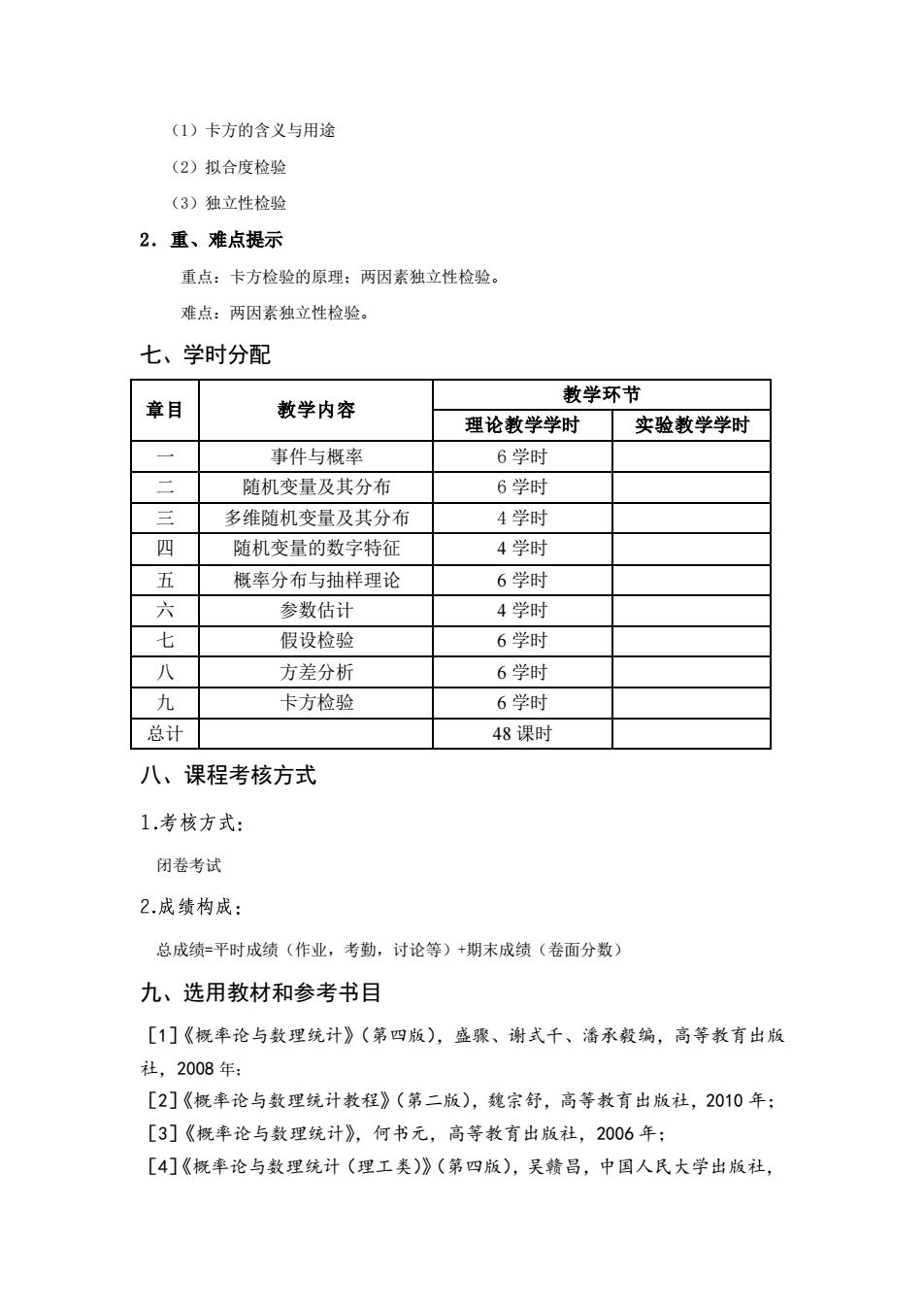
(1)卡方的含义与用途 (2)拟合度检验 (3)独立性检验 2.重、难点提示 重点:卡方检验的原理:两因素独立性检验。 难点:两因素独立性检验。 七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 一 事件与概率 6学时 随机变量及其分布 6学时 三 多维随机变量及其分布 4学时 四 随机变量的数字特征 4学时 五 概率分布与抽样理论 6学时 六 参数估计 4学时 七 假设检验 6学时 八 方差分析 6学时 九 卡方检验 6学时 总计 48课时 八、课程考核方式 1.考核方式: 闭卷考试 2.成绩构成: 总成绩=平时成绩(作业,考勤,讨论等)+期末成绩(卷面分数) 九、选用教材和参考书目 [1]《概率论与数理统计》(第四版),盛骤、谢式千、潘承毅编,高等教育出版 社,2008年: [2]《概率论与数理统计教程》(第二版),魏宗舒,高等教育出版社,2010年: [3]《概率论与数理统计》,何书元,高等教育出版社,2006年: [4]《概率论与数理统计(理工类)》(第四版),吴赣昌,中国人民大学出版社
(1)卡方的含义与用途 (2)拟合度检验 (3)独立性检验 2.重、难点提示 重点:卡方检验的原理;两因素独立性检验。 难点:两因素独立性检验。 七、学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 事件与概率 6 学时 二 随机变量及其分布 6 学时 三 多维随机变量及其分布 4 学时 四 随机变量的数字特征 4 学时 五 概率分布与抽样理论 6 学时 六 参数估计 4 学时 七 假设检验 6 学时 八 方差分析 6 学时 九 卡方检验 6 学时 总计 48 课时 八、课程考核方式 闭卷考试 总成绩=平时成绩(作业,考勤,讨论等)+期末成绩(卷面分数) 九、选用教材和参考书目 [1]《概率论与数理统计》(第四版),盛骤、谢式千、潘承毅编,高等教育出版 社,2008 年; [2]《概率论与数理统计教程》(第二版),魏宗舒,高等教育出版社,2010 年; [3]《概率论与数理统计》,何书元,高等教育出版社,2006 年; [4]《概率论与数理统计(理工类)》(第四版),吴赣昌,中国人民大学出版社

2011年; [5]《现代心理与教育统计学》,张厚粲等著,北京师范大学出版社,2006年; [6]《教育与心理统计学》,张敏强著,人民教育出版社,1999年; [7]《应用数理统计基础》,庄楚强等著,华南理工大学出版社,1992年;
2011 年; [5]《现代心理与教育统计学》, 张厚粲等著,北京师范大学出版社,2006 年; [6]《教育与心理统计学》,张敏强著,人民教育出版社,1999 年; [7]《应用数理统计基础》,庄楚强等著,华南理工大学出版社,1992 年;