
《高等代数》课程教学大纲 课程名称:高等代数 课程类别:学科专业必修课 适用专业:小学教育 考核方式:考试 总学时、学分:48学时、3学分 其中实验学时:0学时 一、课程教学目的 高等代数是小学教育专业数学方向的一门必修课,对学生数学思想 的形成有着重要的意义。高等代数是现代数学的基础知识,是学习其它 数学学科和现代科学知识的必备基础和重要工具。通过本课程的学习, 使学生初步掌握基本的、系统的代数知识和抽象的、严格的代数方法:通 过本课程的学习,为近世代数、泛函分析、微分方程等后续课程提供必要的 代数知识,也为深入理解中学数学打下必要的基础:通过本课程的学习,培 养学生逻辑推理能力、抽象思维能力、分析问题和解决问题的能力。从而 进一步提升学生的数学素养。 二、课程教学要求 要求学生理解本课程的基本概念与基本定理,着重培养学生解决问 题的基本技能:熟悉和掌握本课程所涉及论证的基本思想与基本方法,提 高其抽象思维、逻辑推理和代数运算的能力:通过对典型例题的分析与讲解 让学生学会独立思考,举一反三,提高学生解题的技能与技巧:通过该课程 的学习,使学生对公理化的体系有一定的认识,对代数系统的结构有一定 的了解。 三、先修课程 初等数学 四、课程教学重、难点
《高等代数》课程教学大纲 课程名称:高等代数 课程类别:学科专业必修课 适用专业:小学教育 考核方式:考试 总学时、学分: 48 学时、3 学分 其中实验学时: 0 学时 一、课程教学目的 高等代数是小学教育专业数学方向的一门必修课,对学生数学思想 的形成有着重要的意义。高等代数是现代数学的基础知识,是学习其它 数学学科和现代科学知识的必备基础和重要工具。通过本课程的学习, 使学生初步掌握基本的、系统的代数知识和抽象的、严格的代数方法;通 过本课程的学习,为近世代数、泛函分析、微分方程等后续课程提供必要的 代数知识,也为深入理解中学数学打下必要的基础;通过本课程的学习,培 养学生逻辑推理能力、抽象思维能力、分析问题和解决问题的能力。从而 进一步提升学生的数学素养。 二、课程教学要求 要求学生理解本课程的基本概念与基本定理,着重培养学生解决问 题的基本技能;熟悉和掌握本课程所涉及论证的基本思想与基本方法,提 高其抽象思维、逻辑推理和代数运算的能力;通过对典型例题的分析与讲解, 让学生学会独立思考, 举一反三,提高学生解题的技能与技巧;通过该课程 的学习,使学生对公理化的体系有一定的认识,对代数系统的结构有一定 的了解。 三、先修课程 初等数学 四、课程教学重、难点

重点:线性方程组的解法及其判定,n阶行列式的概念以及性质,数域水 上的维向量空间及其子空间的结构,线性方程组解的判定以及解的结构. 矩阵的运算及它们的运算规律,矩阵的秩及逆矩阵的求法,分块矩阵, 矩阵的初等变换,欧几里得空间中矩阵的相抵、相似、特征值和特征向量, 化二次型为标准形,正定二次型及正定矩阵的判定与证明。 难,点:线性方程组解的计算及判定,级行列式的计算方法及技巧, 向量组的线性相关性,线性方程组解的结构,可逆矩阵,初等矩阵的 应用,矩阵秩的等式和不等式的证明,矩阵的相似、合同、相抵之间 的区别与联系,正定矩阵的判定,化二次型为标准形,正定二次型及 正定矩阵的判定与证明。 五、课程教学方法与教学手段 教学方法灵活多样,自主学习、讨论互动、讲授与讨论相结合等。教学手 段有板书与多媒体相结合、借助微信、QQ等公共平台进行教学互动 等。 六、课程教学内容 第一章线性方程组(6学时) 1.教学内容 (1)高斯(Gauss)-约当(Jordan)算法: (2)线性方程组的解的情况及其判别标准: (3)数域。 2.重、难点提示 重点:高斯(Gauss)-约当(Jordan)算法,线性方程组解的判别: 难点:本章的重点也是难点。 第二章行列式(8学时)
重点:线性方程组的解法及其判定,n阶行列式的概念以及性质,数域K 上的n维向量空间及其子空间的结构,线性方程组解的判定以及解的结构, 矩阵的运算及它们的运算规律,矩阵的秩及逆矩阵的求法,分块矩阵, 矩阵的初等变换,欧几里得空间中矩阵的相抵、相似、特征值和特征向量, 化二次型为标准形,正定二次型及正定矩阵的判定与证明。 难点:线性方程组解的计算及判定,n级行列式的计算方法及技巧, 向量组的线性相关性,线性方程组解的结构,可逆矩阵,初等矩阵的 应用,矩阵秩的等式和不等式的证明,矩阵的相似、合同、相抵之间 的区别与联系,正定矩阵的判定,化二次型为标准形,正定二次型及 正定矩阵的判定与证明。 五、课程教学方法与教学手段 教学方法灵活多样,自主学习、讨论互动、讲授与讨论相结合等。教学手 段有板书与多媒体相结合、借助微信、QQ等公共平台进行教学互动 等。 六、课程教学内容 第一章 线性方程组(6学时) 1.教学内容 (1)高斯(Gauss)-约当(Jordan)算法; (2)线性方程组的解的情况及其判别标准; (3)数域。 2.重、难点提示 重点:高斯(Gauss)-约当(Jordan)算法,线性方程组解的判别; 难点:本章的重点也是难点。 第二章 行列式(8学时)

1.教学内容 (1)n元排列: (2)n阶行列式的定义: (3)行列式的性质: (4)行列式按一行(列)展开: (5)克莱姆(Cramer)法则: (6)行列式按k行(列)展开。 2.重、难点提示 重点:用行列式的性质和按行(列)展开定理计算行列式: 难点:行列式计算的方法和技巧。 第三章线性方程组的进一步理论(8学时) 1.教学内容 (1)n维向量空间: (2)线性相关与线性无关的向量组: (3)向量组的秩: (4)子空间的基与维数: (5)矩阵的秩: (6)线性方程组有解的充分必要条件: (7)齐次线性方程组的解集的结构: (8)非齐次线性方程组的解集的结构。 2.重、难点提示 重点:向量组的线性相关性:线性方程组的基础解系及解的表达: 难点:向量组的线性相关性:线性方程组解的结构。 第四章矩阵的运算(10学时) 1.教学内容 (1)矩阵的运算: (2)特殊矩阵: (3)矩阵乘积的秩与行列式: (4)可逆矩阵:
1.教学内容 (1)n元排列; (2)n阶行列式的定义; (3)行列式的性质; (4)行列式按一行(列)展开; (5)克莱姆(Cramer)法则; (6)行列式按k行(列)展开。 2.重、难点提示 重点:用行列式的性质和按行(列)展开定理计算行列式; 难点:行列式计算的方法和技巧。 第三章 线性方程组的进一步理论(8学时) 1.教学内容 (1)n维向量空间; (2)线性相关与线性无关的向量组; (3)向量组的秩; (4)子空间的基与维数; (5)矩阵的秩; (6)线性方程组有解的充分必要条件; (7)齐次线性方程组的解集的结构; (8)非齐次线性方程组的解集的结构。 2.重、难点提示 重点:向量组的线性相关性;线性方程组的基础解系及解的表达; 难点:向量组的线性相关性;线性方程组解的结构。 第四章 矩阵的运算(10学时) 1.教学内容 (1)矩阵的运算; (2)特殊矩阵; (3)矩阵乘积的秩与行列式; (4)可逆矩阵;

(5)矩阵的分块: (6)正交矩阵·欧几里得空间: (7)线性映射。 2.重、难点提示 重点:矩阵的运算及它们的运算规律:矩阵的秩及逆矩阵的求法:分块矩阵:矩阵的初 等变换: 难点:可逆矩阵:矩阵的分块:初等矩阵在生活中的应用:矩阵秩的等式和不等式的证 明。 第五章矩阵的相抵与相似(10学时) 1.教学内容 (1)等价关系与集合的划分: (2)矩阵的相抵: (3)广义逆矩阵: (4)矩阵的相似: (5)矩阵的特征值和特征向量: (6)矩阵可对角化的条件: (7)实对称矩阵的对角化。 2.重、难点提示 重点:矩阵的相抵、相似、特征值和特征向量: 难点:特征值和特征向量的计算:矩阵相似和相抵之间的区别和联系:矩阵对角化的条 件。 第六章二次型·矩阵的合同(6学时) 1.教学内容 (1)二次型及它的标准型: (2)实二次型的规范形: (3)正定二次型与正定矩阵。 2.重、难点提示 重点:化二次型为标准形:正定二次型及正定矩阵的判定与证明: 难点:本章的重点也是难点
(5)矩阵的分块; (6)正交矩阵•欧几里得空间; (7)线性映射。 2.重、难点提示 重点:矩阵的运算及它们的运算规律;矩阵的秩及逆矩阵的求法;分块矩阵;矩阵的初 等变换; 难点:可逆矩阵;矩阵的分块;初等矩阵在生活中的应用;矩阵秩的等式和不等式的证 明。 第五章 矩阵的相抵与相似(10学时) 1.教学内容 (1)等价关系与集合的划分; (2)矩阵的相抵; (3)广义逆矩阵; (4)矩阵的相似; (5)矩阵的特征值和特征向量; (6)矩阵可对角化的条件; (7)实对称矩阵的对角化。 2.重、难点提示 重点:矩阵的相抵、相似、特征值和特征向量; 难点:特征值和特征向量的计算;矩阵相似和相抵之间的区别和联系;矩阵对角化的条 件。 第六章 二次型•矩阵的合同(6学时) 1.教学内容 (1)二次型及它的标准型; (2)实二次型的规范形; (3)正定二次型与正定矩阵。 2.重、难点提示 重点:化二次型为标准形;正定二次型及正定矩阵的判定与证明; 难点:本章的重点也是难点
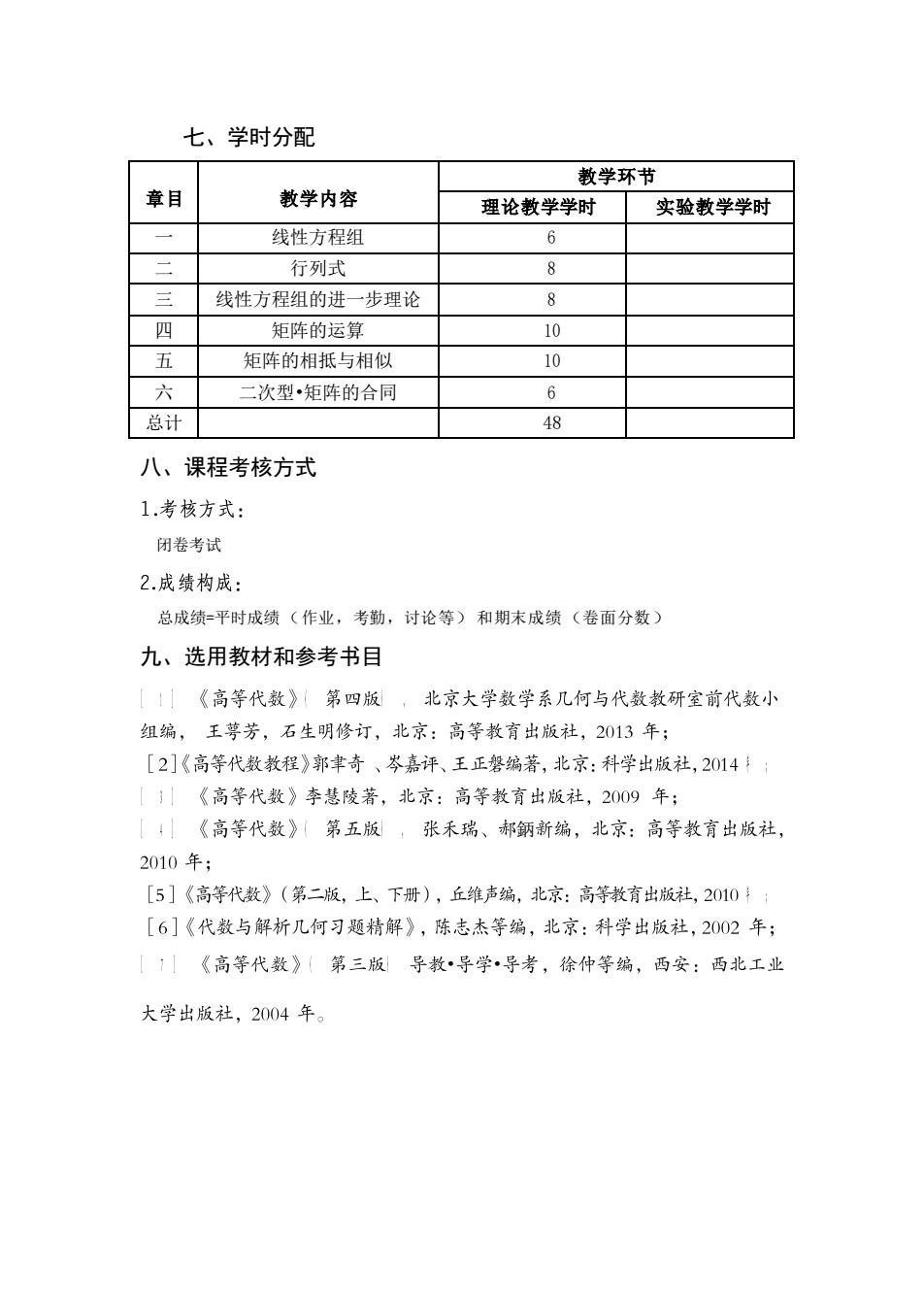
七、学时分配 教学环节 章目 教学内容 理论教学学时 实验教学学时 一 线性方程组 6 行列式 8 三 线性方程组的进一步理论 8 四 矩阵的运算 10 五 矩阵的相抵与相似 10 六 二次型•矩阵的合同 6 总计 48 八、课程考核方式 1.考核方式: 闭卷考试 2.成绩构成: 总成绩=平时成绩(作业,考勤,讨论等)和期末成绩(卷面分数) 九、选用教材和参考书目 [1」《高等代数》(第四版,北京大学数学系几何与代数教研室前代数小 组编,王萼芳,石生明修订,北京:高等教育出版社,2013年; [2]《高等代数教程》郭聿奇、岑嘉评、王正磐编著,北京:科学出版社,2014:: [)《高等代数》李慧陵著,北京:高等教育出版社,2009年: [《高等代数》第五版,张禾瑞、郝鈵新编,北京:高等教育出版社, 2010年; [5]《高等代数》(第二版,上、下册),丘维声编,北京:高等教育出版社,2010: [6]《代数与解析几何习题精解》,陈志杰等编,北京:科学出版社,2002年; [1【《高等代数》(第三版导教导学导考,徐仲等编,西安:西北工业 大学出版社,2004年
七、学时分配 章目 教学内容 教学环节 理论教学学时 实验教学学时 一 线性方程组 6 二 行列式 8 三 线性方程组的进一步理论 8 四 矩阵的运算 10 五 矩阵的相抵与相似 10 六 二次型•矩阵的合同 6 总计 48 八、课程考核方式 闭卷考试 总成绩=平时成绩(作业,考勤,讨论等)和期末成绩(卷面分数) 九、选用教材和参考书目 鈵 • •