中国人民大学：《博弈论》课程教学资源（讲义）第三章完全信息动态博弈.pdf_大学文库

1 § 1 完美信息的动态博弈 § 2 经典动态博弈模型 § 3完全非完美信息动态博弈（两阶段） § 4 动态博弈分析的问题和扩展讨论第三章完全信息动态博弈  动态博弈(Dynamic Games)或序贯行动博弈 Sequential-Move Games 本节讨论完美信息下的动态博弈  参与人的行动有先后顺序  后行动者能够观察到先行动者都干了什么——完美信息 § 1 完美信息的动态博弈  例：欺负他人可以获得快乐，你会欺负他人吗？欺负他人会担心他人的报复。——先行动者在选择行动时要考虑自己的选择对后行动者的影响。  无论何时完成了行动选择，参与人都需要料想他们当前的行动会如何影响未来的行动，包括对手的行动和自己的行动。  于是，参与人是在计算未来结果的基础上决定他们当前的行动选择。  为了做出最优的行动选择，每个参与人须运用怎样的互动思维？ § 1 完美信息的动态博弈 § 1 完美信息的动态博弈解放初，美国总是寻找机会来侵犯我国。对此，毛主席提出了 “人不犯我、我不犯人，人若犯我、我必犯人”的战略方针。  行动空间：美国“犯我”或“不犯我”，中国“犯人”或“不犯人”  行动顺序：美国先行动，我国依美国的行动而后动  支付：  若美国“犯我”，中国“犯人”，则支付向量为(-2,-2)；  若美国“犯我”，中国“不犯人”，则支付向量为(2,-4)；  若美国“不犯我”，中国“犯人”，则支付向量为(3,-5)；  若美国“不犯我”，中国“犯人”，则支付向量为(1,1)。完全信息：对对手的支付情况完全清楚美中军事博弈介绍一种展示和分析动态博弈的技术——博弈树，被称为博弈的扩展式表述，可以将有关博弈的组成的基本要素：参与人、行动、支付表述出来。类似于决策树的概念（这类树形图表达的是单个决策者在一个中性环境中连续不断的决策点或决策结）— —博弈树正是博弈中所有参与人决策树的合并，给出参与人所有可能行动，给出博弈所有可能的结果。 § 1 完美信息的动态博弈  博弈树（game tree）——有限次博弈的扩展式表述犯人犯人不犯人不犯人犯我不犯我美国我国我国 (1,1) (3,-5) (2,-4) (-2,-2) 决策结：行动时点枝：任意决策结出发能够选择的行动终点结：对应一个博弈结果，支付向量初始结路径：由不同枝形成的链构造出不同路径，每条路径都通过有限次行动将你带到博弈的某个终点。  例：两房地产商A、B进行房地产开发。市场需求大、小的概率各占50%。投入： 1亿。  当市场上有两栋楼出售时  需求大时，每栋售价1.4亿，  需求小时，售价7千万；  如果市场上只有一栋楼  需求大时，可卖1.8亿  需求小时，可卖1.1亿引入一个“自然”的外部参与人，随机性事件被假定为一个称为自然的参与人来控制博弈的随机性特征在博弈树中如何表述？ § 1 完美信息的动态博弈

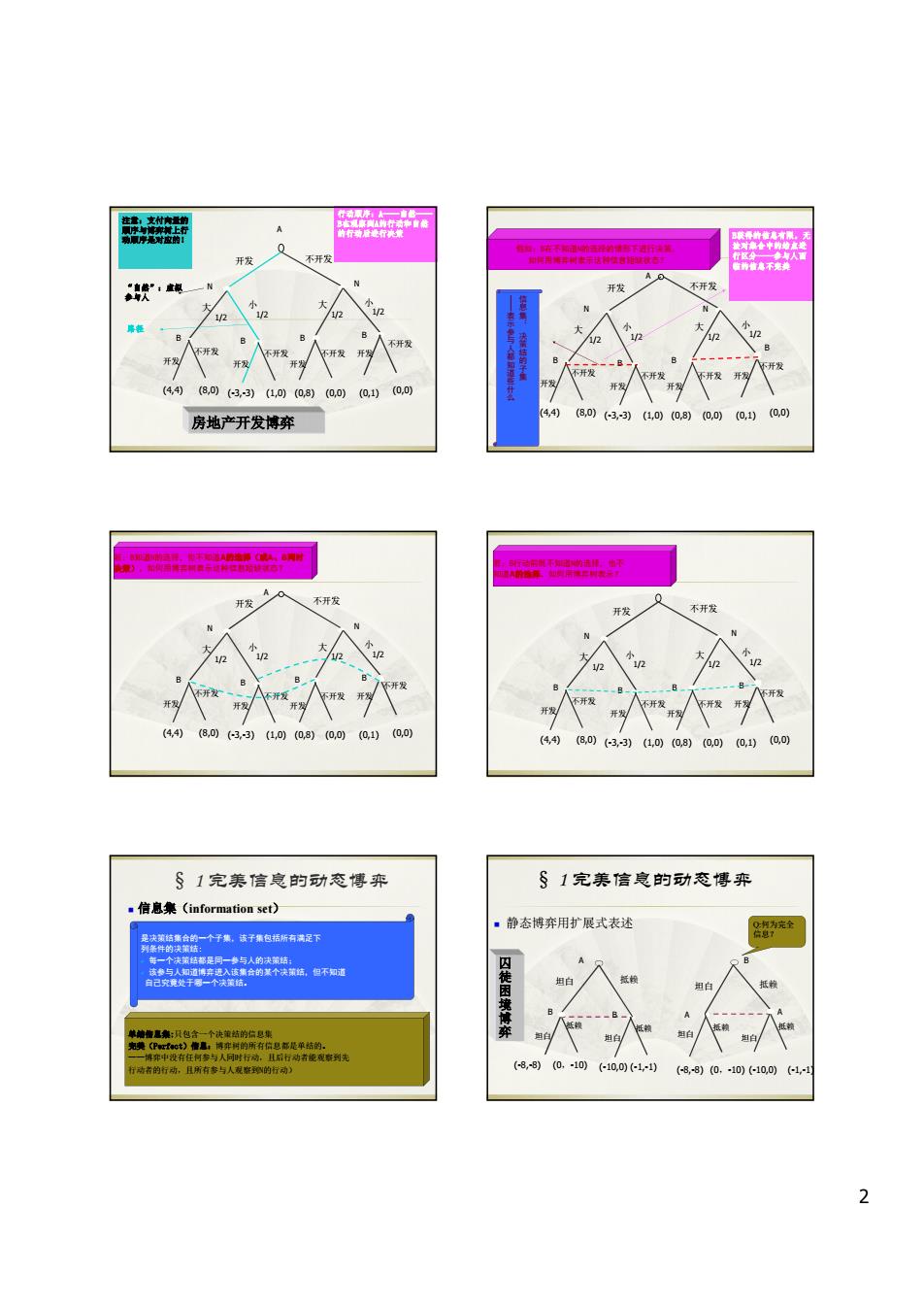
2 A 开发不开发 N N 大小 1/2 1/2 大小 1/2 1/2 B B B B 开发不开发开发不开发开发不开发开发不开发 (4,4) (8,0) (-3,-3) (1,0) (0,8) (0,0) (0,1) (0,0) 注意：支付向量的顺序与博弈树上行动顺序是对应的！ “自然”：虚拟参与人行动顺序：A——自然—— B在观察到A的行动和自然的行动后进行决策路径房地产开发博弈 A 开发不开发 N N 大小 1/2 1/2 大小 1/2 1/2 B B B B 开发不开发开发不开发开发不开发开发不开发 (4,4) (8,0) (-3,-3) (1,0) (0,8) (0,0) (0,1) (0,0) B获得的信息有限，无法对集合中的结点进行区分——参与人面临的信息不完美假如：B在不知道N的选择的情形下进行决策，如何用博弈树表示这种信息短缺状态？信息集：决策结的子集 —— 表示参与人都知道些什么 A 开发不开发 N N 大小 1/2 1/2 大小 1/2 1/2 B B B B 开发不开发开发不开发开发不开发开发不开发 (4,4) (8,0) (-3,-3) (1,0) (0,8) (0,0) (0,1) (0,0) 若：B知道N的选择，但不知道A的选择（或A、B同时决策），如何用博弈树表示这种信息短缺状态？ A 开发不开发 N N 大小 1/2 1/2 大小 1/2 1/2 B B B B 开发不开发开发不开发开发不开发开发不开发 (4,4) (8,0) (-3,-3) (1,0) (0,8) (0,0) (0,1) (0,0) 若：B行动前既不知道N的选择，也不知道A的选择，如何用博弈树表示？  信息集（information set）是决策结集合的一个子集，该子集包括所有满足下列条件的决策结:  每一个决策结都是同一参与人的决策结；  该参与人知道博弈进入该集合的某个决策结，但不知道自己究竟处于哪一个决策结。单结信息集:只包含一个决策结的信息集完美（Perfect）信息：博弈树的所有信息都是单结的。 ——博弈中没有任何参与人同时行动，且后行动者能观察到先行动者的行动，且所有参与人观察到N的行动） § 1 完美信息的动态博弈  静态博弈用扩展式表述 B A A 坦白抵赖坦白抵赖坦白抵赖 (-8,-8) (0，-10) (-10,0) (-1,-1) A 坦白抵赖 B B 坦白抵赖坦白抵赖 (-8,-8) (0，-10) (-10,0) (-1,-1) Q:何为完全信息？囚徒困境博弈 § 1 完美信息的动态博弈

3  但是，参与人可以制定一个行动计划，将每个决策结上的选择都事先规定好，即使这个决策点实际上不会出现。——策略动态博弈中的策略  博弈树中参与人在结点上所选择的单个行动—— 一步/招 (move) 策略：人不犯我、我不犯人；人若犯我、我必犯人美国中国不犯人 (-2,-2) (2,-4) (3,-5) (0,0) 中国美中军事博弈 § 1 完美信息的动态博弈  开发策略：不论A开发不开发，我开发——{开发，开发}  追随策略：A开发我开发，A不开发我不开发——{开发，不开发} ；  对抗策略：A开发我不开发，A 不开发我开发——{不开发，开发} ；  不开发策略:不论A开发不开发我不开发）——{不开发，不开发}；  策略空间为：{开发，开发}、 {开发，不开发} 、{不开发，开发} （不开发，不开发}。 A 开发不开发 B B 开发不开发开发 (-3,-3) (1，0) （0，1) (0,0) 不开发 x x’ A的策略空间为：（开发，不开发）； B有2个可选择的行动，但策略空间中的可选策略有？静态博弈中策略=行动扩展式与策略式的对比 {割耳,割耳} {割耳,默认} {默认,割耳} {默认,默认} 画 -3，-3 -3，-3 1，0 1，0 不画 -4，-3 0，0 -4，-3 0，0 割耳画不画割耳默认默认小孩父亲父亲 (0,0) (-4,-3) (1，-2) (-3,-3) 小孩父亲威胁博弈 § 1 完美信息的动态博弈 {割耳,割耳} {割耳,默认} {默认,割耳} {默认,默认} 画 -3，-3 -3，-3 1，-2 1，-2 不画 -4，-3 0，0 -4，-3 0，0 割耳画不画割耳默认默认小孩父亲父亲 (0,0) (-4,-3) (1，-2) (-3,-3) 三个NE: (不画,{割耳,默认}) (画,{默认，割耳}) (画,{默认，默认}) § 1 完美信息的动态博弈 § 1 完美信息的动态博弈  NE(不画,{割耳,默认})：父亲威胁孩子，如果画，那么就割掉耳朵。孩子相信了威胁，则最好选择不画；如果孩子选择不画，则父亲选择 {割耳,默认}是最优的。  如果孩子足够理性，会相信父亲威胁吗？一旦孩子选择了“画”，父亲无疑选择默认，即策略中事先“规定”的“你画我就割你的耳朵”这一行动届时不会发生。——父亲的威胁是不可置信的(not credible) 。 (不画,{割耳,默认}), (画,{默认，割耳})不会是该博弈合理的均衡。这些包含了不可置信的策略所构成的NE是不能作为模型预测结果的，必须去除。  动态博弈中，各博弈方的策略是他们自己预先设定的，在各个博弈阶段，针对各种情况的相应行为选择的计划。这些策略实际上并没有强制力，而且实施起来有一个过程，因此，只要符合博弈方自己的利益，他们完全可以在博弈过程中改变计划。我们称这种问题为动态博弈中的“相机选择”(Contingent Play)问题。问题：纳什均衡在动态博弈中失效，关键是动态博弈中各博弈方策略选择行为上的“可信性”问题。 § 1 完美信息的动态博弈

4  定义：如果一个完美信息的动态博弈中，各博弈方的策略构成的一个策略组合满足，在整个动态博弈及它的所有子博弈中都构成纳什均衡，那么这个策略组合称为该动态博弈的一个“子博弈精炼纳什均衡”。  子博弈精炼纳什均衡能够排除均衡策略中不可信的威胁和承诺，因此是真正稳定的。  子博弈精炼纳什均衡必须对博弈方在所有选择节点处的选择做出规定，包括最终不在均衡路径上的节点。  逆推归纳法是求完美信息动态博弈子博弈精炼纳什均衡的基本方法。 § 1 完美信息的动态博弈  定义：由一个动态博弈第一阶段以外的某阶段开始的后续博弈阶段构成的，有初始信息集和进行博弈所需要的全部信息，能够自成一个博弈的原博弈的一部分，称为原动态博弈的一个“子博弈”。乙甲不借借分不分（1，0）（0，4）（2，2）乙（-1，0）注：（1）从一个单点决策节开始，之后的所有枝节包含其中（2）子博弈不能分割信息集 § 1 完美信息的动态博弈  NE：（不画，{割，默认}）(不是子博弈I的均衡)  NE：（画， {默认，割} ）（不是子博弈II的均衡）  NE：（画， {默认，默认} ）不包含不可置信的行动的策略——子博弈精炼纳什均衡（能够排除保证实际发生的动态行为与事前规定的策略是一致的，因此是真正稳定的）。子博弈Ⅱ (-3,-3) (1,-2) 子博弈Ⅰ 小孩父亲默认 (-4,-3) (0,0) 威胁博弈 § 1 完美信息的动态博弈  定义：从动态博弈的最后一个阶段博弈方的行为开始分析，逐步倒推回前一个阶段相应博弈方的行为选择，一直到第一个阶段的分析方法，称为“逆推归纳法”。  逻辑基础：动态博弈中先行动的理性的博弈方，在前面阶段选择行为时必然会先考虑后行为博弈方在后面阶段中将会怎样选择行为，只有在博弈的最后一个阶段选择的，不再有后续阶段牵制的博弈方，才能直接作出明确选择。而当后面阶段博弈方的选择确定以后，前一阶段博弈方的行为也就容易确定了。 § 1 完美信息的动态博弈 § 1 完美信息的动态博弈  5个海盗抢到了100颗宝石，每一颗都有一样的大小和一样贵重的价值，经过商议，他们决定将宝石这样分配： a 抽签决定自己的号码1，2，3，4，5。 b 首先，由1号提出分配方案，然后5人进行表决，如果同意这种方案的人达到半数，就按照1号的提案进行分配，否则，他将被扔入大海喂鲨鱼，然后由接下来的人继续重复提议。  假设每个海盗都是绝顶聪明，也不互相合作，而且每个都追求最大限度得到金币宝石  1号海盗如何提议？海盗分赃 § 1 完美信息的动态博弈  5号海盗：分给自己100枚宝石  4号海盗：分给自己100枚宝石并赞成自己；5号海盗被分得0枚，反对无用  3号海盗：分给5号海盗1枚并得到5号的同意；分给自己 99枚，自己同意；分给4号海盗0枚，4号反对也无用  2号海盗：分给4号1枚得到4号的同意；分给自己99枚，自己也同意；3、5号反对无用。  1号海盗：分给3、5号海盗各1枚，获得3、5号的同意；分给自己98枚，自己同意；分给2、4号海盗0枚，他们会反对但不起作用。  均衡结果是（98，0，1，0，1）海盗分赃

5 §2 经典动态博弈模型一、斯塔克博格模型二、讨价还价博弈企业1为领头企业，首先选择自己的产量；企业2为跟随者，根据企业1的产量选择自己的产量 Q  q1  q2 , P  P(Q)  8  Q 2 c1  c2  1 1 1 1 1 1 2 2 1 u qP(Q)cq q[8(q q )] q 2 6q1q1q2 q1 2 2 2 2 2 1 2 2 2 u q P(Q)c q q [8(q q )] q 2 6q2 q1q2 q2     逆向归纳法求解SPNE结果。第二阶段企业2的问题为 2 * 2 2 2 1 2 2 1 2 2 arg max ( , ) 6 q q u q q q q q q      一阶条件，也就是反应函数为一、Stackelberg寡头竞争模型 * 2 2 1 1 1 ( ) (6 ) 2 q s q q    与cournot模型中企业2的反应函数相同  企业1会预测到企业2的反应，因此第一阶段的问题为 1 * 2 max ( , ) 6 1 1 2 1 1 2 1 q u q q q q q q     代入企业2的反应函数得 q1 *=3 则 q2 *=1.5 产量支付厂商1 3单位 4.5 厂商2 1.5单位 2.25 古诺博弈均衡：厂商1 2单位 4 厂商2 2单位 4 一、Stackelberg寡头竞争模型  比较stackelberg模型和counot模型结果： stackelberg均衡 counot均衡为什么？  企业1存在先动优势（first-mover advantage）产量支付产量支付厂商1 3单位 4.5 2 4 厂商2 1.5单位 2.25 2 4  与cournot模型相比，企业2拥有信息优势反而对自己不利一、Stackelberg寡头竞争模型二、讨价还价模型  讨价还价：两人就如何分享1万元现金进行谈判，并定下如下规则：  先由甲提出一个分割比例，对甲提出的比例乙可以接受也可以拒绝；  如果乙拒绝甲的方案，则他自己应提出另一个方案，让甲选择接受与否；  ……  只要任何一方接受对方的方案，博弈就结束，而如果方案被拒绝，则被拒绝方案与以后的讨价还价不再有关系。  每一次，一方提出一个方案，与另一方选择是否接受为一个回合，讨价还价每多进行一个回合，由于谈判费用和利息损失等，双方的利益都要打一个折扣（其值在0—1之间，我们称为消耗系数。二、讨价还价模型  利用逆推归纳法分析：  第三回合，甲出S，双方的利益分别为 2 S和 2 (10000- S)（由于乙必须接受，故S通常为10000）  第二回合，乙的选择。乙知道一旦博弈进行到第三回合，甲的策略及双方的得益。如果乙已经拒绝第一回合甲的方案，此时他该怎样出价才能使自己的利益最大化？  原则：任何一博弈方只要利益不少于下一回合自己出价时的利益，就愿意接受对方的出价  故乙在第二回合能让甲接受的，也是可能使自己得最大利益的S2，应满足使甲的二、三回合得益相同，此时，乙的得益为（10000-S）

6 二、讨价还价模型  第一回合：甲一开始就知道第三回合的得益，也知道乙在第二回合的出价，因此，进行到第三回合自己的得益为 2 S，而乙则会满足于得到10000- 2 S，因此，如果甲在第一回合就给乙10000- 2 S，而同时自己又能得到比 2 S更大的利益，那当然是更理想的。实现这一想法只要令S1满足10000- S1 =10000- 2 S，即S1 =10000-10000- 2 S即可。二、讨价还价模型三回合讨价还价：在第三回合，乙必须接受甲的方案。 1 1 2 不接受，出S 接受不接受，出S2 接受出S1 [ , (10000 )] 2 2 S   S ( ,10000 ) 1 1 S  S [ , (10000 )] 2 2  S  S S  S 2 S S S 2 1 1000010000  第一回合：（S1，10000-S1）第二回合：（S2, (10000-S2)）第三回合：（ 2S,  2(10000-S) ）三、讨价还价博弈甲的得益乙的得益第三回合  2S 2(10000-S) 第二回合 S2 (10000-S2)=10000- 2S 第一回合 S1 10000-S1 到了第三回合，甲将提出：S=10000 S2=S S1=10000-10000  + 2S=10000(1-  + 2 ) 当=0.5时，甲得益 - 2有最大值为0.25 二、讨价还价模型二、讨价还价模型  三回合讨价还价博弈结果的讨论  当0.5<<1时，越大，甲的得益越大，乙的得益越小；  当0<<0.5时，越小，甲的得益越小，乙的得益越大。  启示：乙仗以讨价还价的筹码：跟甲拖时间。  现实的例子：利润分配、债务纠纷、财产继承等。二、讨价还价模型  无限回合讨价还价  与三回合博弈不同的地方在于：无限回合的讨价还价博弈在第三回合并不会强制结束，只要双方互不接受对方的出价方案，则博弈就要不断进行下去，奇数回合由甲出价乙选择是否接受，偶数则相反。  对于无限回合博弈，从第一回合还是从第三回合开始，并不影响最终的结果。二、讨价还价模型 S S 2 1 10000 10000  S   1 * 10000 S      1 10000 10000 * S 2 S S    10000 10000  S S  1 第三回合出价第一回合出价

7 § 3 完全非完美信息动态博弈（两阶段）一、标准模型二、国际竞争和最优关税一、标准模型  博弈中有四个博弈方，分别称为博弈方1、博弈方2、博弈方3和博弈方4；  第一阶段是博弈方1和博弈方2的选择阶段，他们同时在各自的可选策略（行为）集合A1和A2中分别选择 a1和a2；  第二阶段是博弈方3和博弈方4的选择阶段，他们在看到博弈方1和博弈方2的选择 a1 和 a2以后，同时在各自的可选策略（行为）集合 A1和A2中分别选择 a3和a4；一、标准模型  现实经济中不少博弈问题与上述标准模型基本一致。如国际竞争和最优关税博弈问题，两个制订关税的国家就是标准博弈的博弈方1和2，两国各自的一个相互进行产量竞争的企业就是模型中的博弈方3和4。  各博弈方的得益都取决于所有博弈方的策略即博弈方i的得益是各个博弈方所选择策略的多元函数 ui =ui (a1 ,a2 ,a3 ,a4 ) 一、标准模型  由于两阶段有同时选择的博弈仍然是动态博弈，而且仍然有完全和完美信息的特征，因此，分析这种博弈问题的基本方法仍然是逆推归纳法，核心均衡概念仍然是子博弈完美纳什均衡。  由于存在同时选择，每个阶段不再是单人最优化问题，而是一个静态博弈。二、国际竞争和最优关税  问题描述：两个国家，i=1,2，国家政府制定关税税率，企业制造产品供本国消费及出口，消费者在国内市场购买本国企业和国外企业生产的产品。如果国家i的市场总产量为，则市场出清价格为其中，国家i的企业为国内生产，并出口，企业的边际成本为c，没有固定成本。产品出口时企业要承担关税成本，如果国家j的关税税率为，则企业i支付的关税为 Qi i i i i i i p (Q )  a Q ,Q  h  e i h i e j t i j e t 二、国际竞争和最优关税  博弈的顺序如下：政府同时选择关税；企业观察到关税税率后，同时选择其提供国内消费和出口的产量。企业i的收益为其利润额；政府i的收益=国家i的消费者剩余+企业i的利润+从企业j收取的关税收入

8 二、国际竞争和最优关税 * j e * j h i j i i j i i i j i  [a  (h  e )]h  [a  (e  h )]e  c(h  e )  t e 厂商的得益函数为：第二阶段厂商选择：由于企业的利润可以分为国内市场的利润和国外市场的利润之和，且国内市场的利润取决于hi 和国外市场的利润取决于ei和 e*j ，因此企业利润最大值问题可分为下列两个最大值问题： ( , , , , , ) i i i j i j i j    t t h h e e 3 2 , 3 * * j i i i a c t e a c t h       max{ [ ( ) ]} * 0 h a h e c i i j hi     max{ [ ( ) ] } * 0 i i j j i e e a e h c t e i      和分别求导可得：二、国际竞争和最优关税 3 2 , 3 * * j i i i a c t e a c t h       第一阶段政府选择：先把第二阶段根据厂商选择得到结果代入政府得益，再求最优化： , 1,2 9 , 9 4( ) , 3 3 ( ) 9 ( 2 ) 9 ( ) 18 [2( ) ] ( , ) max ( , ) * * * 2 2 * 2 * *                    i a c e a c h a c t a c t a c t a c t t a c t w t t w t t i i i i i j i i i i j i i j 政府的得益函数； ( , , , , , ) i i i j i j i j w  w t t h h e e i j i i j  h  e    t e 2 ( ) 2 1 二、国际竞争和最优关税 § 4 动态博弈分析的问题和扩展讨论一、逆推归纳法的问题二、颤抖手均衡一、逆推归纳法的问题 1、逆推归纳法只能分析明确设定的博弈问题，要求博弈的结构，包括次序、规则和得益情况等都非常清楚，并且各个博弈方了解博弈结构，相互知道对方了解博弈结构。这些可能有脱实际的可能。 2、逆推归纳法也不能分析比较复杂的动态博弈。 3、遇到两条路径利益相同的情况时，逆推归纳法就会发生选择困难。 4、对博弈方的理性要求太高，不仅要求所有博弈方都有高度的理性，不允许犯任何错误，而且要求所有博弈方相互了解和信任对方的理性，对理性有相同的理解，或进一步有“理性的共同知识”。二、颤抖手均衡泽尔滕1975年使用策略式博弈引入了颤抖手均衡概念，它是对纳什均衡的改进。基本思想：在任何一个博弈中，每个局中人都有一定的可能性犯错误，就像人在抓东西时，手会颤抖，这样就抓不到他想抓的东西一样，那么一个策略组合，只有当它允许所有参与人都可能犯错误也始终是参与人的最优选择时才是一种均衡。泽尔滕将非均衡事件的发生解释为“颤抖”：当一个参与人突然发现一个不该发生的事件发生时（即博弈偏离均衡路径），他把这个不该发生的事件归结为其他参与人非蓄意的错误

9  意义:颤抖手均衡是一种精炼纳什均衡。  大致说来，泽尔腾(1975)假定，在博弈中存在一个数值极小但又不为0的概率，即在每个博弈者选择对他来说所有可行的一项策略时，可能会偶尔出错，这就是所谓的“颤抖之手”。因此，一个博弈者的均衡策略是在考虑到其对手可能“颤抖”(偶尔出错)的情况下对其对手策略选择所作的最好的策略回应。二、颤抖手均衡  以下图中的博弈为例：  在这个博弈中(D,L)和(U,R)都是纳什均衡,其中(D,L)对博弈方1 较为有利,(U,R)对博弈方2较为有利。  在不考虑选择和行为偏差的情况下,这两种纳什均衡都是稳定的, 即为该博弈可能的结果。如果考虑到博弈方的选择和行为可能出现的偏差,情况就会发生一定的变化。  假设博弈方2有可能选R,那么据此,博弈方1选U,进而博弈方2选R。博弈方2 L R D U 博弈方1 二、颤抖手均衡二、颤抖手均衡  因为从这个策略组合出发,不管博弈方2是否有偏离R的可能,博弈方1都没有必要偏离U；对博弈方2来说,虽然博弈方1从U偏离到D对他的利益有不利的影响,但只要博弈方1偏离的可能性不超过2/3,那么自己改变策略并不合理。  [假设博弈方1偏离U的概率为a,那么不偏离的概率为1-a,则2(1-a)=a,得到a=2/3]  因此,(U,R)对于概率较小的偶然偏差来说具有稳定性,我们称具有这样性质的策略组合为“颤抖手均衡 ”。显然,(D,L)就不是一个颤抖手均衡。因为如果博弈方 2偏离L则博弈方1必定偏离D.  [假设博弈方2偏离L的概率为a,那么不偏离的概率为1-a,则博弈方1继续选D应满足 10(1-a)+2a>10(1-a)+6a,得到a9(1-a)+6a,得到a=<1/5] 博弈方2 L R D U 博弈方1 二、颤抖手均衡  通过这两个例子的对比可以看出,一个策略组合要是一个颤抖手均衡,首先必须是一个纳什均衡,其次是不能包含任何“弱劣策略”,也就是偏离对偏离者没有损失的策略。包含“弱劣策略” 的纳什均衡不可能是颤抖手均衡,因为它们经不起任何非完全理性的“扰动”,缺乏在有限理性条件下的稳定性。  通过上述分析可以看出,颤抖手均衡就是一种精炼子博弈完美纳什均衡的概念。能够通过颤抖手均衡检验的子博弈纳什均衡,在动态博弈中的稳定性必然更强,预测也更加可靠一些。  当然,颤抖手均衡并没有解决博弈方犯错误的问题,因此也不能保证它的预测一定就是实际博弈的结果,即使动态博弈中有唯一的颤抖手均衡

中国人民大学：《博弈论》课程教学资源（讲义）第三章 完全信息动态博弈

中国人民大学：《博弈论》课程教学资源（讲义）第三章完全信息动态博弈