
“平面向量数量积的物理背景及其含义”说课稿 宁夏银川唐徕回民中学马海军 说课内容:普通高中课程标准实验教科书(人教A版)《数学必修4》第 二章第四节“平面向量的数量积”的第一课时-一平面向量数量积的物理背景及 其含义 下面,我从背景分析、教学目标设计、课堂结构设计、教学过程设计、教 学媒体设计及教学评价设计六个方面对本节课的思考进行说明。 一、背景分析 1、学习任务分析 平面向量的数量积是继向量的线性运算之后的又一重要运算,也是高中数 学的一个重要概念,在数学、物理等学科中应用十分广泛。本节内容教材共安 排两课时,其中第一课时主要研究数量积的概念,第二课时主要研究数量积的 坐标运算,本节课是第一课时。 本节课的主要学习任务是通过物理中“功”的事例抽象出平面向量数量积 的概念,在此基础上探究数量积的性质与运算律,使学生体会类比的思想方法, 进一步培养学生的抽象概括和推理论证的能力。其中数量积的概念既是对物理 背景的抽象,又是研究性质和运算律的基础。同时也因为在这个概念中,既有 长度又有角度,既有形又有数,是代数、几何与三角的最佳结合点,不仅应用 广泛,而且很好的体现了数形结合的数学思想,使得数量积的概念成为本节课 的核心概念,自然也是本节课教学的重点。 2、学生情况分析 学生在学习本节内容之前,己熟知了实数的运算体系,掌握了向量的概念 及其线性运算,具备了功等物理知识,并且初步体会了研究向量运算的一般方 法:即先由特殊模型(主要是物理模型)抽象出概念,然后再从概念出发,在 与实数运算类比的基础上研究性质和运算律。这为学生学习数量积做了很好的
“平面向量数量积的物理背景及其含义”说课稿 宁夏银川唐徕回民中学 马海军 说课内容:普通高中课程标准实验教科书(人教 A 版)《数学必修 4》第 二章第四节“平面向量的数量积”的第一课时-平面向量数量积的物理背景及 其含义。 下面,我从背景分析、教学目标设计、课堂结构设计、教学过程设计、教 学媒体设计及教学评价设计六个方面对本节课的思考进行说明。 一、 背景分析 1、学习任务分析 平面向量的数量积是继向量的线性运算之后的又一重要运算,也是高中数 学的一个重要概念,在数学、物理等学科中应用十分广泛。本节内容教材共安 排两课时,其中第一课时主要研究数量积的概念,第二课时主要研究数量积的 坐标运算,本节课是第一课时。 本节课的主要学习任务是通过物理中“功”的事例抽象出平面向量数量积 的概念,在此基础上探究数量积的性质与运算律,使学生体会类比的思想方法, 进一步培养学生的抽象概括和推理论证的能力。其中数量积的概念既是对物理 背景的抽象,又是研究性质和运算律的基础。同时也因为在这个概念中,既有 长度又有角度,既有形又有数,是代数、几何与三角的最佳结合点,不仅应用 广泛,而且很好的体现了数形结合的数学思想,使得数量积的概念成为本节课 的核心概念,自然也是本节课教学的重点。 2、学生情况分析 学生在学习本节内容之前,已熟知了实数的运算体系,掌握了向量的概念 及其线性运算,具备了功等物理知识,并且初步体会了研究向量运算的一般方 法:即先由特殊模型(主要是物理模型)抽象出概念,然后再从概念出发,在 与实数运算类比的基础上研究性质和运算律。这为学生学习数量积做了很好的

铺垫,使学生倍感亲切。但也正是这些干扰了学生对数量积概念的理解,一方 面,相对于线性运算而言,数量积的结果发生了本质的变化,两个有形有数的 向量经过数量积运算后,形却消失了,学生对这一点是很难接受的:另一方面, 由于受实数乘法运算的影响,也会造成学生对数量积理解上的偏差,特别是对 性质和运算律的理解。因而本节课教学的难点数量积的概念。 二、教学目标设计 《普通高中数学课程标准(实验)》对本节课的要求有以下三条: (1)通过物理中“功”等事例,理解平面向量数量积的含义及其物理意义。 (2)体会平面向量的数量积与向量投影的关系。 (3)能用运数量积表示两个向量的夹角,会用数量积判断两个平面向量的 垂直关系。 从以上的背景分析可以看出,数量积的概念既是本节课的重点,也是难点。 为了突破这一难点,首先无论是在概念的引入还是应用过程中,物理中“功” 的实例都发挥了重要作用。其次,作为数量积概念延伸的性质和运算律,不仅 能够使学生更加全面深刻地理解概念,同时也是进行相关计算和判断的理论依 据。最后,无论是数量积的性质还是运算律,都希望学生在类比的基础上,通 过主动探究来发现,因而对培养学生的抽象概括能力、推理论证能力和类比思 想都无疑是很好的载体。 综上所述,结合“课标”要求和学生实际,我将本节课的教学目标定为: 1、了解平面向量数量积的物理背景,理解数量积的含义及其物理意义: 2、体会平面向量的数量积与向量投影的关系,掌握数量积的性质和运算律, 并能运用性质和运算律进行相关的运算和判断:
铺垫,使学生倍感亲切。但也正是这些干扰了学生对数量积概念的理解,一方 面,相对于线性运算而言,数量积的结果发生了本质的变化,两个有形有数的 向量经过数量积运算后,形却消失了,学生对这一点是很难接受的;另一方面, 由于受实数乘法运算的影响,也会造成学生对数量积理解上的偏差,特别是对 性质和运算律的理解。因而本节课教学的难点数量积的概念。 二、 教学目标设计 《普通高中数学课程标准(实验)》 对本节课的要求有以下三条: (1)通过物理中“功”等事例,理解平面向量数量积的含义及其物理意义。 (2)体会平面向量的数量积与向量投影的关系。 (3)能用运数量积表示两个向量的夹角,会用数量积判断两个平面向量的 垂直关系。 从以上的背景分析可以看出,数量积的概念既是本节课的重点,也是难点。 为了突破这一难点,首先无论是在概念的引入还是应用过程中,物理中“功” 的实例都发挥了重要作用。其次,作为数量积概念延伸的性质和运算律,不仅 能够使学生更加全面深刻地理解概念,同时也是进行相关计算和判断的理论依 据。最后,无论是数量积的性质还是运算律,都希望学生在类比的基础上,通 过主动探究来发现,因而对培养学生的抽象概括能力、推理论证能力和类比思 想都无疑是很好的载体。 综上所述,结合“课标”要求和学生实际,我将本节课的教学目标定为: 1、了解平面向量数量积的物理背景,理解数量积的含义及其物理意义; 2、体会平面向量的数量积与向量投影的关系,掌握数量积的性质和运算律, 并能运用性质和运算律进行相关的运算和判断;
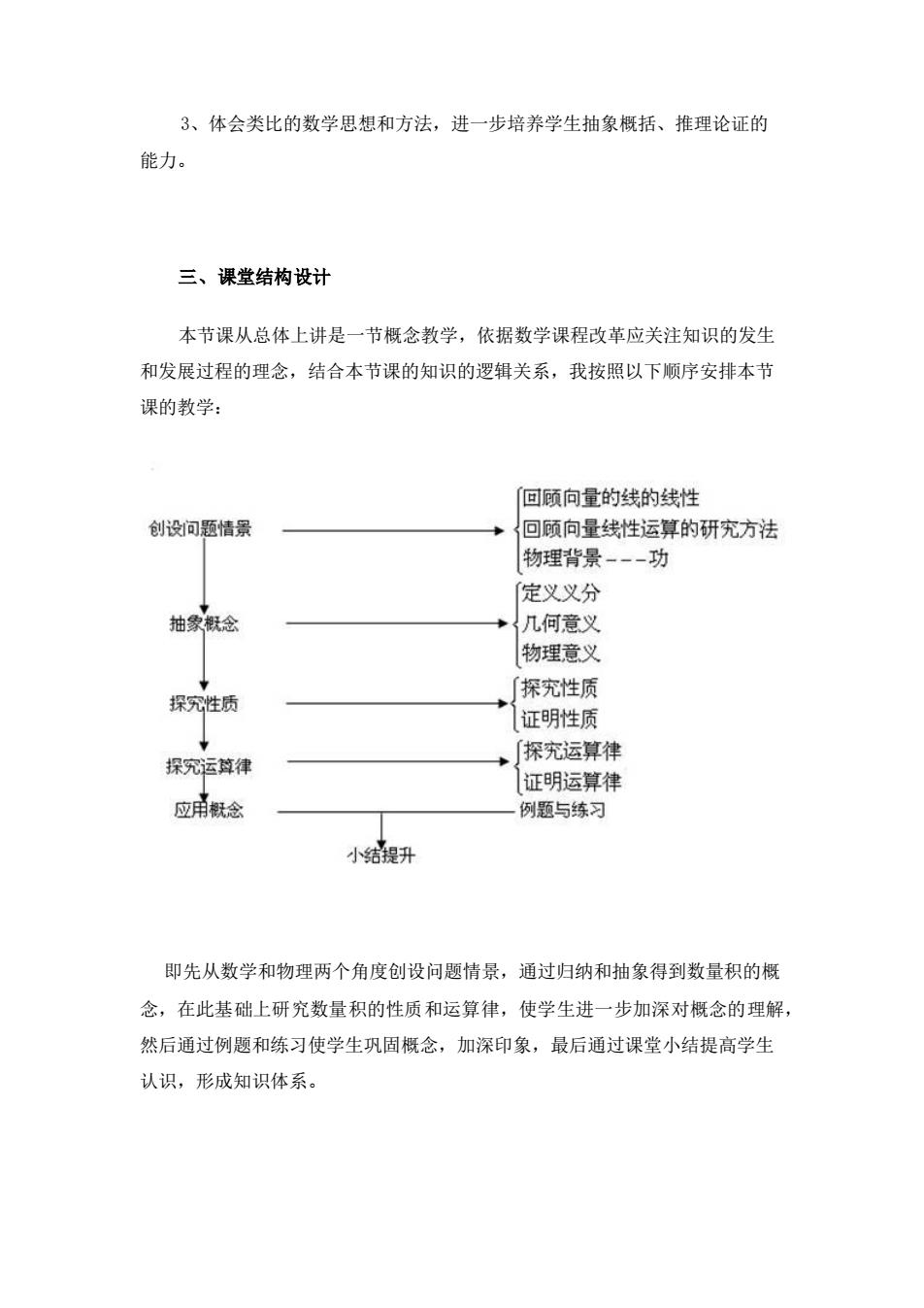
3、体会类比的数学思想和方法,进一步培养学生抽象概括、推理论证的 能力。 三、课堂结构设计 本节课从总体上讲是一节概念教学,依据数学课程改革应关注知识的发生 和发展过程的理念,结合本节课的知识的逻辑关系,我按照以下顺序安排本节 课的教学: 回顾向量的线的线性 创设问题情景 回顾向量线性运算的研究方法 物理背景-功 「定义义分 抽象概念 +几何意义 物理意义 ∫探究性质 探究性质 证明性质 探究运算律 ∫探究运算律 证明运算律 应角献念 例题与练习 小结提升 即先从数学和物理两个角度创设问题情景,通过归纳和抽象得到数量积的 念,在此基础上研究数量积的性质和运算律,使学生进一步加深对概念的理解, 然后通过例题和练习使学生巩固概念,加深印象,最后通过课堂小结提高学生 认识,形成知识体系
3、体会类比的数学思想和方法,进一步培养学生抽象概括、推理论证的 能力。 三、课堂结构设计 本节课从总体上讲是一节概念教学,依据数学课程改革应关注知识的发生 和发展过程的理念,结合本节课的知识的逻辑关系,我按照以下顺序安排本节 课的教学: 即先从数学和物理两个角度创设问题情景,通过归纳和抽象得到数量积的概 念,在此基础上研究数量积的性质和运算律,使学生进一步加深对概念的理解, 然后通过例题和练习使学生巩固概念,加深印象,最后通过课堂小结提高学生 认识,形成知识体系

四、教学媒体设计 和“大纲”教材相比,“课标”教材在本节课的内容安排上,虽然将向量 的夹角在“平面向量基本定理”一节提前做了介绍,但却将原来分两节课完成 的内容合并成一节,相比较而言本节课的教学任务加重了许多。为了保证教学 任务的完成,顺利实现本节课的教学目标,考虑到本节课的实际特点,在教学 媒体的使用上,我的设想主要有以下两点: 1、制作高效实用的电脑多媒体课件,主要作用是改变相关内容的呈现方式, 以此来节约课时,增加课堂容量。 2、设计科学合理的板书(见下),一方面使学生加深对主要知识的印象, 另一方面使学生清楚本节内容知识间的逻辑关系,形成知识网络。 平面向量数量积的物理背景及其含义 一、数量积的概念 二、数量积的性 质 四、应用与提高 1、概 : 例1: 2、概念强调(1)记 法 例2: (2)“规定” 三、数量积的运算 例3: 3、几何意义: 4、物理意义:
四、 教学媒体设计 和“大纲”教材相比,“课标”教材在本节课的内容安排上,虽然将向量 的夹角在“平面向量基本定理”一节提前做了介绍,但却将原来分两节课完成 的内容合并成一节,相比较而言本节课的教学任务加重了许多。为了保证教学 任务的完成,顺利实现本节课的教学目标,考虑到本节课的实际特点,在教学 媒体的使用上,我的设想主要有以下两点: 1、制作高效实用的电脑多媒体课件,主要作用是改变相关内容的呈现方式, 以此来节约课时,增加课堂容量。 2、设计科学合理的板书(见下),一方面使学生加深对主要知识的印象, 另一方面使学生清楚本节内容知识间的逻辑关系,形成知识网络。 平面向量数量积的物理背景及其含义 一、 数量积的概念 二、数量积的性 质 四、应用与提高 1、 概 念: 例 1: 2、 概念强调 (1)记 法 例 2: (2)“规定” 三、数量积的运算 律 例 3: 3、几何意义: 4、物理意义:

五、教学过程设计 课标指出:数学教学过程是教师引导学生进行学习活动的过程,是教师和 学生间互动的过程,是师生共同发展的过程。为有序、有效地进行教学,本节 课我主要安排以下六个活动: 活动一:创设问题情景,激发学习兴趣 正如教材主编寄语所言,数学是自然的,而不是强加于人的。平面向量的 数量积这一重要概念,和向量的线性运算一样,也有其数学背景和物理背景, 为了体现这一点,我设计以下几个问题: 问题1:我们已经研究了向量的哪些运算?这些运算的结果是什么? 问题2:我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研 究了这种运算的? 期望学生回答:物理模型→概念→性质→运算律→应用 问题3:如图所示,一物体在力F的作用下产生位移S
五、 教学过程设计 课标指出:数学教学过程是教师引导学生进行学习活动的过程,是教师和 学生间互动的过程,是师生共同发展的过程。为有序、有效地进行教学,本节 课我主要安排以下六个活动: 活动一:创设问题情景,激发学习兴趣 正如教材主编寄语所言,数学是自然的,而不是强加于人的。平面向量的 数量积这一重要概念,和向量的线性运算一样,也有其数学背景和物理背景, 为了体现这一点,我设计以下几个问题: 问题 1:我们已经研究了向量的哪些运算?这些运算的结果是什么? 问题 2:我们是怎么引入向量的加法运算的?我们又是按照怎样的顺序研 究了这种运算的? 期望学生回答:物理模型→概念→性质→运算律→应用 问题 3:如图所示,一物体在力 F 的作用下产生位移 S

(1)力F所做的功=一 (2)请同学们分析这个公式的特点: W(功)是量, F(力)是量, S(位移)是量, a是 问题1的设计意图在于使学生了解数量积的数学背景,让学生明白本节课所要研究的 数量积与向量的加法、减法及数乘一样,都是向量的运算,但与向量的线性运算相比,数 量积运算又有其特殊性,那就是其结果发生了本质的变化。 问题2的设计意图在于使学生在与向量加法类比的基础上明了本节课的研 究方法和顺序,为教学活动指明方向。 问题3的设计意图在于使学生了解数量积的物理背景,让学生知道,我们 研究数量积绝不仅仅是为了数学自身的完善,而是有其客观背景和现实意义的, 从而产生了进一步研究这种新运算的愿望。同时,也为抽象数量积的概念做好 铺垫。 活动二:探究数量积的概念 1、概念的抽象 在分析“功”的计算公式的基础上提出问题4 问题4:你能用文字语言来表述功的计算公式吗?如果我们将公式中的力与 位移推广到一般向量,其结果又该如何表述?
(1)力 F 所做的功 W= 。 (2)请同学们分析这个公式的特点: W(功)是 量, F(力)是 量, S(位移)是 量, α是 。 问题 1 的设计意图在于使学生了解数量积的数学背景,让学生明白本节课所要研究的 数量积与向量的加法、减法及数乘一样,都是向量的运算,但与向量的线性运算相比,数 量积运算又有其特殊性,那就是其结果发生了本质的变化。 问题 2 的设计意图在于使学生在与向量加法类比的基础上明了本节课的研 究方法和顺序,为教学活动指明方向。 问题 3 的设计意图在于使学生了解数量积的物理背景,让学生知道,我们 研究数量积绝不仅仅是为了数学自身的完善,而是有其客观背景和现实意义的, 从而产生了进一步研究这种新运算的愿望。同时,也为抽象数量积的概念做好 铺垫。 活动二:探究数量积的概念 1、概念的抽象 在分析“功”的计算公式的基础上提出问题 4 问题 4:你能用文字语言来表述功的计算公式吗?如果我们将公式中的力与 位移推广到一般向量,其结果又该如何表述?

学生通过思考不难回答:功是力与位移的大小及其夹角余弦的乘积:两个 向量的大小及其夹角余弦的乘积。这样,学生事实上已经得到数量积概念的文 字表述了,在此基础上,我进一步明晰数量积的概念, 2、概念的明晰 已知两个非零向量“与b,它们的夹角为c,我们把数量1云1·18 1cosc叫做2与5的数量积(或内积),记作:a.i,即:G.6=1a 1·18|cosa 在强调记法和“规定”后,为了让学生进一步认识这一概念,提 出问题5 问题5:向量的数量积运算与线性运算的结果有什么不同?影响数量积大 小的因素有哪些?并完成下表: 角Q的范围 0°≤a<90 =90° 0°<a≤180° a·b的符号 通过此环节不仅使学生认识到数量积的结果与线性运算的结果有着本质的 不同,而且认识到向量的夹角是决定数量积结果的重要因素,为下面更好地理 解数量积的性质和运算律做好铺垫。 3、探究数量积的几何意义 这个问题教材是这样安排的:在给出向量数量积的概念后,只介绍了向 量投影的定义,直到讲完例1后,为了证明运算律的第三条才直接以结论的形 式呈现给学生,我觉得这样安排似乎不太自然,还不如在给出向量投影的概念
学生通过思考不难回答:功是力与位移的大小及其夹角余弦的乘积;两个 向量的大小及其夹角余弦的乘积。这样,学生事实上已经得到数量积概念的文 字表述了,在此基础上,我进一步明晰数量积的概念。 2、概念的明晰 已知两个非零向量 与 ,它们的夹角为 ,我们把数量 ︱ ︱·︱ ︱cos 叫做 与 的数量积(或内积),记作: · ,即: · = ︱ ︱·︱ ︱cos 在强调记法和“规定”后 ,为了让学生进一步认识这一概念,提 出问题 5 问题 5:向量的数量积运算与线性运算的结果有什么不同?影响数量积大 小的因素有哪些?并完成下表: 角 的范围 0°≤ <90° =90° 0°< ≤180° · 的符号 通过此环节不仅使学生认识到数量积的结果与线性运算的结果有着本质的 不同,而且认识到向量的夹角是决定数量积结果的重要因素,为下面更好地理 解数量积的性质和运算律做好铺垫。 3、探究数量积的几何意义 这个问题教材是这样安排的:在给出向量数量积的概念后,只介绍了向 量投影的定义,直到讲完例 1 后,为了证明运算律的第三条才直接以结论的形 式呈现给学生,我觉得这样安排似乎不太自然,还不如在给出向量投影的概念

后,直接由学生自己归纳得出,所以做了调整。为此,我首先给出给出向量投 影的概念,然后提出问题5。 如图,我们把|b|cos&(|a|cosa)叫做向量b在a方向上(a在 B方向上)的投影,记做:OB,=|B|cosc 问题6:数量积的几何意义是什么? 这样做不仅让学生从“形”的角度重新认识数量积的概念,从中体会数 量积与向量投影的关系,同时也更符合知识的连贯性,而且也节约了课时。 4、研究数量积的物理意义 数量积的概念是由物理中功的概念引出的,学习了数量积的概念后,学生 就会明白功的数学本质就是力与位移的数量积。为此,我设计以下问题一方面 使学生尝试计算数量积,另一方面使学生理解数量积的物理意义,同时也为数 量积的性质埋下伏笔。 问题7: (1)请同学们用一句话来概括功的数学本质:功是力与位移的数量积。 (2)尝试练习:一物体质量是10千克,分别做以下运动: ①、在水平面上位移为10米: ②、竖直下降10米:
后,直接由学生自己归纳得出,所以做了调整。为此,我首先给出给出向量投 影的概念,然后提出问题 5。 如图,我们把│ │cos (│ │cos )叫做向量 在 方向上( 在 方向上)的投影,记做:OB1=│ │cos 问题 6:数量积的几何意义是什么? 这样做不仅让学生从“形”的角度重新认识数量积的概念,从中体会数 量积与向量投影的关系,同时也更符合知识的连贯性,而且也节约了课时。 4、研究数量积的物理意义 数量积的概念是由物理中功的概念引出的,学习了数量积的概念后,学生 就会明白功的数学本质就是力与位移的数量积。为此,我设计以下问题 一方面 使学生尝试计算数量积,另一方面使学生理解数量积的物理意义,同时也为数 量积的性质埋下伏笔。 问题 7: (1) 请同学们用一句话来概括功的数学本质:功是力与位移的数量积 。 (2)尝试练习:一物体质量是 10 千克,分别做以下运动: ①、在水平面上位移为 10 米; ②、竖直下降 10 米;

③、竖直向上提升10米: ④、沿倾角为30度的斜面向上运动10米: 分别求重力做的功。 活动三:探究数量积的运算性质 1、性质的发现 教材中关于数量积的三条性质是以探究的形式出现的,为了很好地完成这 一探究活动,在完成上述练习后,我不失时机地提出问题8: (1)将尝试练习中的①②③的结论推广到一般向量,你能得到哪些结论? (2)比较1a·b1与1a1×|6|的大小,你有什么结论? 在学生讨论交流的基础上,教师进一步明晰数量积的性质,然后再由学生 利用数量积的定义给予证明,完成探究活动。 2、明晰数量积的性质
③、竖直向上提升 10 米; ④、沿倾角为 30 度的斜面向上运动 10 米; 分别求重力做的功。 活动三:探究数量积的运算性质 1、性质的发现 教材中关于数量积的三条性质是以探究的形式出现的,为了很好地完成这 一探究活动,在完成上述练习后,我不失时机地提出问题 8: (1)将尝试练习中的① ② ③的结论推广到一般向量,你能得到哪些结论? (2)比较︱ · ︱与︱ ︱×︱ ︱的大小,你有什么结论? 在学生讨论交流的基础上,教师进一步明晰数量积的性质,然后再由学生 利用数量积的定义给予证明,完成探究活动。 2、明晰数量积的性质

数量积的性质 设a和b都是非零向量,则 1、a16一期8.8-0 2、当a与6同向时,|a,石1-|a116|,当a与石反向时, 1a.31=-1a1181,特别地,a.a-1a1'或1a1=vaa 3、|a.6|≤|a|×161 3、性质的证明 这样设计体现了教师只是教学活动的引领者,而学生才是学习活动的主 体,让学生成为学习的研究者,不断地体验到成功的喜悦,激发学生参与学习 活动的热情,不仅使学生获得了知识,更培养了学生由特殊到一般的思维品质。 活动四:探究数量积的运算律 1、运算律的发现 关于运算律,教材仍然是以探究的形式出现,为此,首先提出问题9
3、性质的证明 这样设计体现了教师只是教学活动的引领者,而学生才是学习活动的主 体,让学生成为学习的研究者,不断地体验到成功的喜悦,激发学生参与学习 活动的热情,不仅使学生获得了知识,更培养了学生由特殊到一般的思维品质。 活动四:探究数量积的运算律 1、运算律的发现 关于运算律,教材仍然是以探究的形式出现,为此,首先提出问题 9