
三角函数模型的简单应用-一潮汐问题 浙江省温州市第二十二中学高洪武 教学目标: 巩固已知三角函数,求给定自变量对应的函数值: 己知三角函数值,求相应自变量的值: 利用图象解三角不等式 利用二分法求相应方程的近似解: 培养学生数学应用意识: 提高学生利用信息技术处理一些实际计算的能力: 教学重点: 用三角函数模型刻画潮汐变化规律,用函数思想解决具有周期变化的实际问题。 教学难点: 对问题实际意义的数学解释,从实际问题中抽象出三角函数模型。 教学媒体: 几何画板 敕学流程:
三角函数模型的简单应用-潮汐问题 浙江省温州市第二十二中学 高洪武 教学目标: 巩固已知三角函数,求给定自变量对应的函数值; 已知三角函数值,求相应自变量的值; 利用图象解三角不等式; 利用二分法求相应方程的近似解; 培养学生数学应用意识; 提高学生利用信息技术处理一些实际计算的能力; 教学重点: 用三角函数模型刻画潮汐变化规律,用函数思想解决具有周期变化的实际问题。 教学难点: 对问题实际意义的数学解释,从实际问题中抽象出三角函数模型。 教学媒体: 几何画板 教学流程:

·给出出港▣水深数据,提出问题 根据散点图形特征,选择适当的函数拟合 厌解心故模型 利用函数模型解决实际问题 「反思解题过程,总结解题方法,提炼数学思想 敕学过程 1.情景展示,新课导入 【师】经过前面的学习,大家知道,在客观现实世界中存在着大量的周期性变化现 象,而要定量地去刻画这些现象,我们通常需要借助于三角函数这一重要数学模型。这节 课我们将来学习三角函数模型的简单应用。 (教师板书课题:S1.6三角函数模型的简单应用) 【师】请看这样一副画面:这是我们所熟悉的温州市区著名景点-一江心屿(图 1),江心屿上面有座峙庙一江心峙(图2),旁边这位人物是(稍微停顿)我们温州南 宋时期著名状元诗人-一王十朋(图3)。(学生不是很熟悉,已经淡忘了)他在江心峙中 题了一副非常知名对联。(学生又想起来了) (呈现对联)上联是:云朝朝朝朝朝朝朝朝散:下联是:朝长长长长长长长长消。 (师生齐朗诵,课堂气氛活跃)
教学过程: 1.情景展示,新课导入 【师】经过前面的学习,大家知道,在客观现实世界中存在着大量的周期性变化现 象,而要定量地去刻画这些现象,我们通常需要借助于三角函数这一重要数学模型。这节 课我们将来学习三角函数模型的简单应用。 (教师板书课题:§1.6 三角函数模型的简单应用) 【师】请看这样一副画面:这是我们所熟悉的温州市区著名景点-江心屿(图 1),江心屿上面有座峙庙-江心峙(图 2),旁边这位人物是(稍微停顿)我们温州南 宋时期著名状元诗人-王十朋(图 3)。(学生不是很熟悉,已经淡忘了)他在江心峙中 题了一副非常知名对联。(学生又想起来了) (呈现对联)上联是:云朝朝朝朝朝 朝朝朝散;下联是:朝长长 长长长 长长长消。 (师生齐朗诵,课堂气氛活跃)

图1 图2 图3 【师】在这里,诗人王十朋巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面, 当然他对瓯江潮水的描述也是感性的。今天我们将从数学的视角理性地研究有关瓯江潮水 落的一些实际问题。 2.问题提出,探究解决 【师】老师想问大家一个问题:若干年后,如果在座的各位有机会当上船长的话, 当你的船只要到某个港口去,你作为船长,你希望知道关于那个港口的一些什么情况? 【生】水深情况。 【师】是的,我们要到一个陌生的港口时,是非常想得到一张有关那个港口的水深 与时间的对应关系数值表。那么这张表格是如何产生的呢?请同学们看下面这个问题。 问题探究1:如图所示,下面是瓯江江心屿码头在某年某个季节每天的时间与水深 的关系表 时间0.001.003.006.008.009.0012.0015.0018.0021.0024.00 水深5.06.257.55.02.842.55.07.55.02.55.0 【师】请同学们仔细观察表格中的数据,你能够从中得到一些什么信息? 【生】(思考中)发现水深的最大值是7.5米,最小值是2.5米。 【师】水的深度变化有什么特点吗? 【生】水的深度开始由5.0米增加到7.5米,后逐渐减少一直减少到2.5,又开始逐 渐变深,增加到7.5米后,又开始减少
【师】在这里,诗人王十朋巧妙地运用了叠字诗展现了瓯江潮水涨落的壮阔画面, 当然他对瓯江潮水的描述也是感性的。今天我们将从数学的视角理性地研究有关瓯江潮水 涨落的一些实际问题。 2.问题提出,探究解决 【师】老师想问大家一个问题:若干年后,如果在座的各位有机会当上船长的话, 当你的船只要到某个港口去 ,你作为船长,你希望知道关于那个港口的一些什么情况? 【生】水深情况。 【师】是的,我们要到一个陌生的港口时,是非常想得到一张有关那个港口的水深 与时间的对应关系数值表。那么这张表格是如何产生的呢?请同学们看下面这个问题。 问题探究 1:如图所示,下面是瓯江江心屿码头在某年某个季节每天的时间与水深 的关系表: 时间 0.00 1.00 3.00 6.00 8.00 9.00 12.00 15.00 18.00 21.00 24.00 水深 5.0 6.25 7.5 5.0 2.84 2.5 5.0 7.5 5.0 2.5 5.0 【师】请同学们仔细观察表格中的数据,你能够从中得到一些什么信息? 【生】(思考中)发现水深的最大值是 7.5 米,最小值是 2.5 米。 【师】水的深度变化有什么特点吗? 【生】水的深度开始由 5.0 米增加到 7.5 米,后逐渐减少一直减少到 2.5,又开始逐 渐变深,增加到 7.5 米后,又开始减少
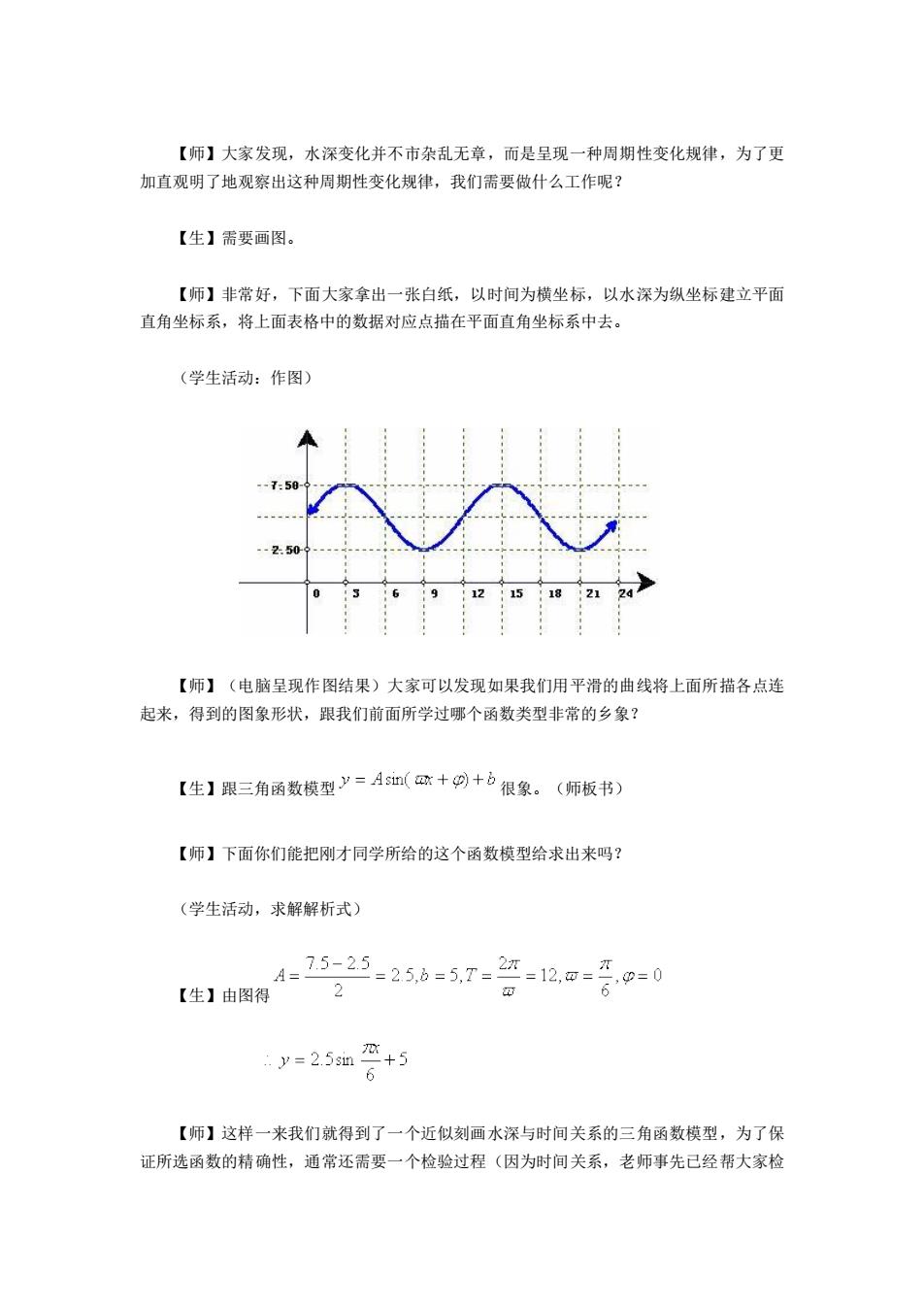
【师】大家发现,水深变化并不市杂乱无章,而是呈现一种周期性变化规律,为了更 加直观明了地观察出这种周期性变化规律,我们需要做什么工作呢? 【生】需要画图。 【师】非常好,下面大家拿出一张白纸,以时间为横坐标,以水深为纵坐标建立平面 直角坐标系,将上面表格中的数据对应点描在平面直角坐标系中去。 (学生活动:作图) 2 15 g212a 【师】(电脑呈现作图结果)大家可以发现如果我们用平滑的曲线将上面所描各点连 起来,得到的图象形状,跟我们前面所学过哪个函数类型非常的乡象? 【生】果三角函数模型y=A5如(+网+力很象。《师板书) 【师】下面你们能把刚才同学所给的这个函数模型给求出来吗? (学生活动,求解解析式) 2 y=25m+5 6 【师】这样一来我们就得到了一个近似刻画水深与时间关系的三角函数模型,为了保 证所选函数的精确性,通常还需要一个检验过程(因为时间关系,老师事先已经帮大家检
【师】大家发现,水深变化并不市杂乱无章,而是呈现一种周期性变化规律,为了更 加直观明了地观察出这种周期性变化规律,我们需要做什么工作呢? 【生】需要画图。 【师】非常好,下面大家拿出一张白纸,以时间为横坐标,以水深为纵坐标建立平面 直角坐标系,将上面表格中的数据对应点描在平面直角坐标系中去。 (学生活动:作图) 【师】(电脑呈现作图结果)大家可以发现如果我们用平滑的曲线将上面所描各点连 起来,得到的图象形状,跟我们前面所学过哪个函数类型非常的乡象? 【生】跟三角函数模型 很象。(师板书) 【师】下面你们能把刚才同学所给的这个函数模型给求出来吗? (学生活动,求解解析式) 【生】由图得 【师】这样一来我们就得到了一个近似刻画水深与时间关系的三角函数模型,为了保 证所选函数的精确性,通常还需要一个检验过程(因为时间关系,老师事先已经帮大家检

验过了,这里就不检验,同学们可以下去检验下)有了这个模型,我们要制定一张一天24 内整时刻的水深表,就是件非常容易的事情了,下面同学算一下在4时的时候水深是多少? (学生计算,最后教师呈现水深关于时间的数值表) 时1.002.00 3.00 4.005.006.007.008.009.0010.0011.0012.00 刻 水5.000 6.250 7.165 7.5006.2505.0003.7542.8352.5002.835 3.7545.000 深 时13.00 14.00 15.00 16.00 17.0018.0019.0020.00 21.0022.00 23.00 24.00 刻 水7 6.250 7.165 7.500 7.1656.2505.0003.7542.8352.5002.835 3.7545.000 【师】有了水深关于时间的函数模型以后,作为船长考虑的问题还没有结束,因为船 只在进出港时,每艘船只的吃水深度是不一样,下面我们就看一看把这两方面的情况都考 虑进去的一个问题 问题探究2:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少 要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能 呆多久? 【师】货船能够进入港口所需要满足的条件是什么? (师生一起分析) 【师】只有当“实际水深≥吃水深度+安全间隙”时,船只才可以进去或离开港口。 怎样用数学语言将这一条件给转述出来呢? 25m24+15 【生 02 6 (师生齐分析)解三角不等式,通常我们是算去边界值,然后再确定解的范围。 【1◆-02
验过了,这里就不检验,同学们可以下去检验下)有了这个模型,我们要制定一张一天 24 内整时刻的水深表,就是件非常容易的事情了,下面同学算一下在 4 时的时候水深是多少? (学生计算,最后教师呈现水深关于时间的数值表) 时 刻 1.00 2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 水 深 5.000 6.250 7.165 7.500 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000 时 刻 13.00 14.00 15.00 16.00 17.00 18.00 19.00 20.00 21.00 22.00 23.00 24.00 水 深 6.250 7.165 7.500 7.165 6.250 5.000 3.754 2.835 2.500 2.835 3.754 5.000 【师】有了水深关于时间的函数模型以后,作为船长考虑的问题还没有结束,因为船 只在进出港时,每艘船只的吃水深度是不一样,下面我们就看一看把这两方面的情况都考 虑进去的一个问题: 问题探究 2:一艘货船的吃水深度(船底与水面的距离)为 4 米,安全条例规定至少 要有 1.5 米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能 呆多久? 【师】货船能够进入港口所需要满足的条件是什么? (师生一起分析) 【师】只有当“实际水深 吃水深度+安全间隙”时,船只才可以进去或离开港口。 怎样用数学语言将这一条件给转述出来呢? 【生】 ,即 , (师生齐分析)解三角不等式,通常我们是算去边界值,然后再确定解的范围。 【师】令
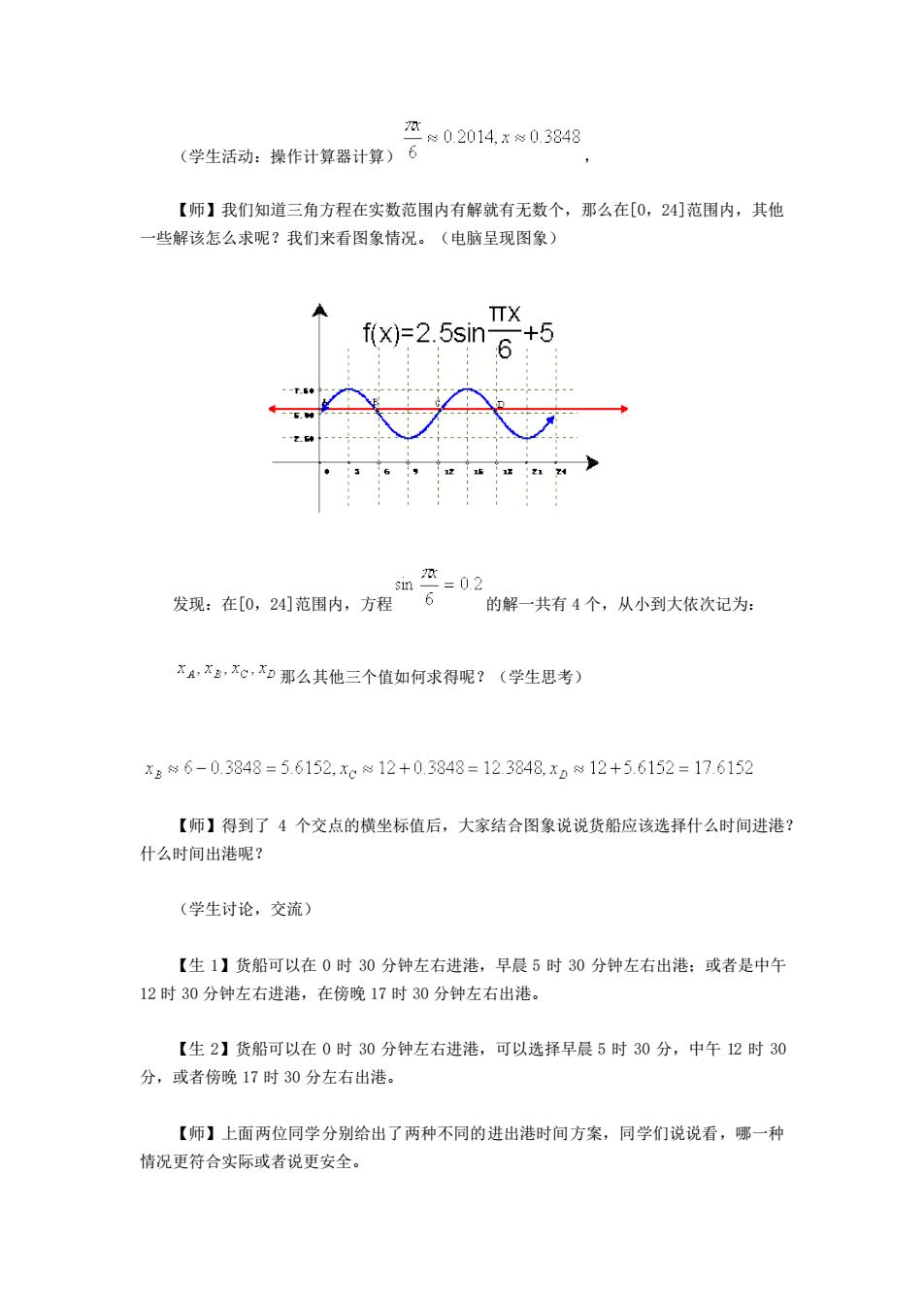
学生活动:操作计算器计算)602014x≈03848 【师】我们知道三角方程在实数范围内有解就有无数个,那么在[0,24]范围内,其他 一些解该怎么求呢?我们来看图象情况。(电脑呈现图象) A TTX f(x)=2.5sin 6 +5 发观在0,2内02 解一共有4个,从小到大依次记为: xA,不多,Xc,x0那么其他三个值如何求得呢?(学生思考) xBg6-0.3848=5.6152,xc≈12+03848=12.3848,x0g12+5.6152=17.6152 【师】得到了4个交点的横坐标值后,大家结合图象说说货船应该选择什么时间进港? 什么时间出港呢? (学生讨论,交流) 【生1】货船可以在0时30分钟左右进港,早晨5时30分钟左右出港:或者是中午 12时30分钟左右进港,在傍晚17时30分钟左右出港。 【生2】货船可以在0时30分钟左右进港,可以选择早晨5时30分,中午12时30 分,或者傍晚17时30分左右出港。 【师】上面两位同学分别给出了两种不同的进出港时间方案,同学们说说看,哪一种 情况更符合实际或者说更安全
(学生活动:操作计算器计算) , 【师】我们知道三角方程在实数范围内有解就有无数个,那么在[0,24]范围内,其他 一些解该怎么求呢?我们来看图象情况。(电脑呈现图象) 发现:在[0,24]范围内,方程 的解一共有 4 个,从小到大依次记为: 那么其他三个值如何求得呢?(学生思考) 【师】得到了 4 个交点的横坐标值后,大家结合图象说说货船应该选择什么时间进港? 什么时间出港呢? (学生讨论,交流) 【生 1】货船可以在 0 时 30 分钟左右进港,早晨 5 时 30 分钟左右出港;或者是中午 12 时 30 分钟左右进港,在傍晚 17 时 30 分钟左右出港。 【生 2】货船可以在 0 时 30 分钟左右进港,可以选择早晨 5 时 30 分,中午 12 时 30 分,或者傍晚 17 时 30 分左右出港。 【师】上面两位同学分别给出了两种不同的进出港时间方案,同学们说说看,哪一种 情况更符合实际或者说更安全

(学生讨论,最后确定方案1为安全方案,因为当实际水深小于安全深度时,货船尽 管没有行驶,但是搁浅后船身完全可以馅入淤泥,即使后来水位上涨,也很可能船身不再 上浮) 【师】大家看看刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的 吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货 船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随若船身自 身重量的减小,船身会上浮,换句话说,随着货物的卸载,货船的安全深度不再向开始那 样一直是一个常数,现在它也是一个关于时间的变量,而实际水深也一直在变化,这样 来当两者都在改变的时候,我们又改如何选择进出港时间呢?请看下面问题: 问题探究3:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少 要有1.5米的安全间隙(船底与洋底的距离),该船在2:00开始卸货,吃水深度以每小 时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域? 【师】题目中“必须停止卸货”,是在货船即将面临什么危险的时候呢? (学生讨论) 【生】当实际水深快要小于或等于安全水深的时候,就必修停止卸货。 【师】那么我们先把货船安全需要满足的条件给写出来: 安全即需要:实际水深之安全水深 25m0+5≥55-03x-2) 即: 【师】这样的不等式大家会解吗? 【生】不会 【师】用代数的方法不会解的时候,我们不妨从几何的角度来考虑这个问题。(电脑 作图并呈现)
(学生讨论,最后确定方案 1 为安全方案,因为当实际水深小于安全深度时,货船尽 管没有行驶,但是搁浅后船身完全可以馅入淤泥,即使后来水位上涨,也很可能船身不再 上浮) 【师】大家看看刚才整个过程,货船在进港,在港口停留,到后来离开港口,货船的 吃深深度一直没有改变,也就是说货船的安全深度一直没有改变,但是实际情况往往是货 船载满货物进港,在港口卸货,在卸货的过程中,由物理学的知识我们知道,随着船身自 身重量的减小,船身会上浮,换句话说,随着货物的卸载,货船的安全深度不再向开始那 样一直是一个常数,现在它也是一个关于时间的变量,而实际水深也一直在变化,这样一 来当两者都在改变的时候,我们又改如何选择进出港时间呢?请看下面问题: 问题探究 3:一艘货船的吃水深度(船底与水面的距离)为 4 米,安全条例规定至少 要有 1.5 米的安全间隙(船底与洋底的距离),该船在 2:00 开始卸货,吃水深度以每小 时 0.3 米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域? 【师】题目中“必须停止卸货”,是在货船即将面临什么危险的时候呢? (学生讨论) 【生】当实际水深快要小于或等于安全水深的时候,就必修停止卸货。 【师】那么我们先把货船安全需要满足的条件给写出来: 安全即需要:实际水深 安全水深 即: , 【师】这样的不等式大家会解吗? 【生】不会 【师】用代数的方法不会解的时候,我们不妨从几何的角度来考虑这个问题。(电脑 作图并呈现)
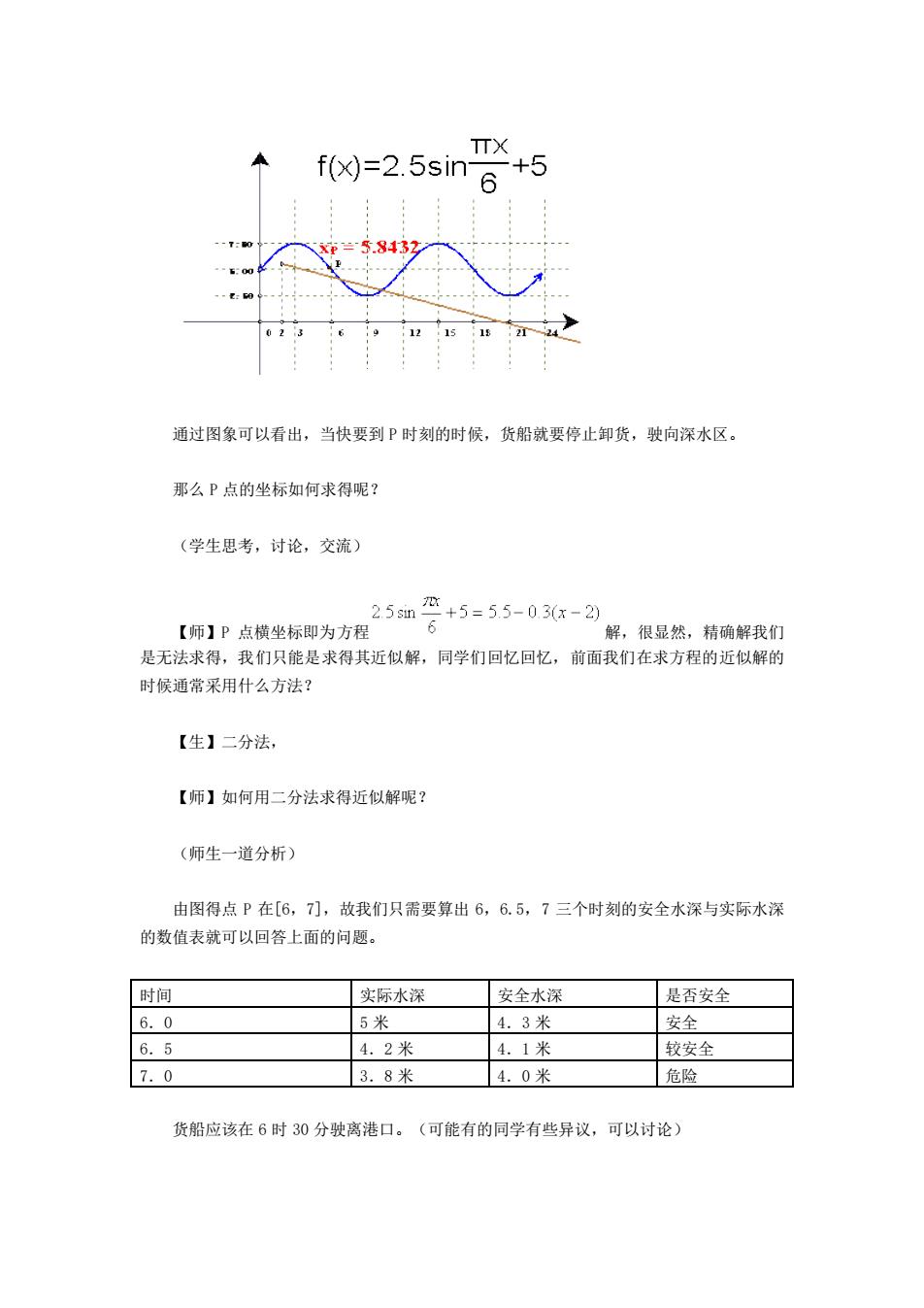
TTX f(x)=2.5sin 6 +5 e5.8432 15 通过图象可以看出,当快要到P时刻的时候,货船就要停止卸货,驶向深水区。 那么P点的坐标如何求得呢? (学生思考,讨论,交流) 25m2店+5=55-030x-29 【师】P点横坐标即为方程 解,很显然,精确解我们 是无法求得,我们只能是求得其近似解,同学们回忆回忆,前面我们在求方程的近似解的 时候通常采用什么方法? 【生】二分法, 【师】如何用二分法求得近似解呢? (师生一道分析) 由图得点P在[6,7],故我们只需要算出6,6.5,7三个时刻的安全水深与实际水深 的数值表就可以回答上面的问题。 时间 实际水深 安全水深 是否安全 6.0 5米 4.3米 安全 6.5 4.2米 4.1米 较安全 7.0 3.8米 4.0米 危险 货船应该在6时0分驶离港口。(可能有的同学有些异议,可以讨论)
通过图象可以看出,当快要到 P 时刻的时候,货船就要停止卸货,驶向深水区。 那么 P 点的坐标如何求得呢? (学生思考,讨论,交流) 【师】P 点横坐标即为方程 解,很显然,精确解我们 是无法求得,我们只能是求得其近似解,同学们回忆回忆,前面我们在求方程的近似解的 时候通常采用什么方法? 【生】二分法, 【师】如何用二分法求得近似解呢? (师生一道分析) 由图得点 P 在[6,7],故我们只需要算出 6,6.5,7 三个时刻的安全水深与实际水深 的数值表就可以回答上面的问题。 时间 实际水深 安全水深 是否安全 6.0 5 米 4.3 米 安全 6.5 4.2 米 4.1 米 较安全 7.0 3.8 米 4.0 米 危险 货船应该在 6 时 30 分驶离港口。(可能有的同学有些异议,可以讨论)
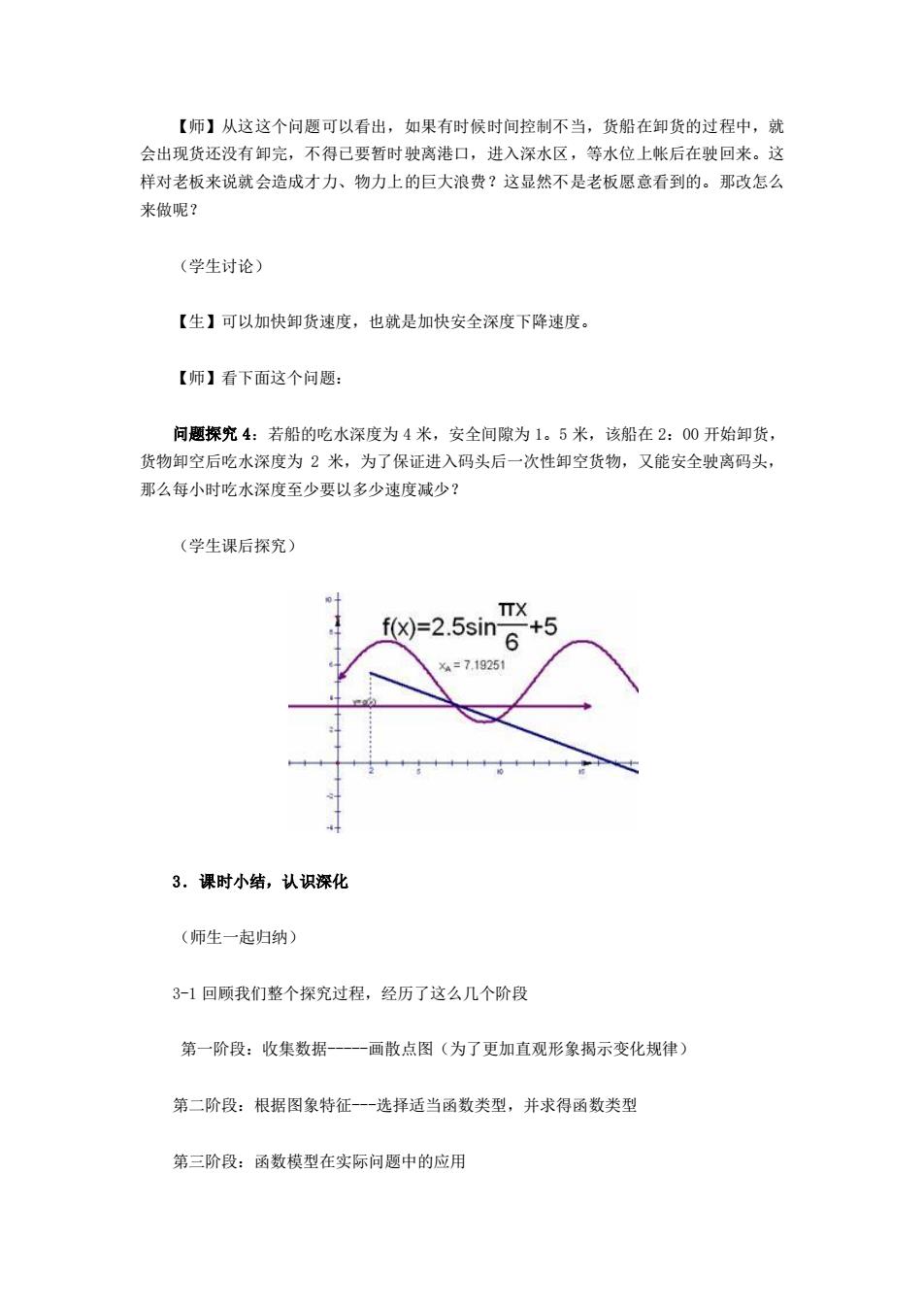
【师】从这这个问恩可以看出,如果有时候时间控制不当,货船在卸货的过程中,就 会出现货还没有卸完,不得己要暂时驶离港口,进入深水区,等水位上帐后在驶回来。这 样对老板来说就会造成才力、物力上的巨大浪费?这显然不是老板愿意看到的。那改怎么 来做呢? (学生讨论) 【生】可以加快卸货速度,也就是加快安全深度下降速度。 【师】看下面这个问题: 问题探究4:若船的吃水深度为4米,安全间隙为1.5米,该船在2:00开始卸货, 货物卸空后吃水深度为2米,为了保证进入码头后一次性卸空货物,又能安全驶离码头, 那么每小时吃水深度至少要以多少速度减少? (学生课后探究) TX f(X)=2.5sin 6 +5 ×4=7.1925 3.课时小结,认识深化 (师生一起归纳〉 3-1回顾我们整个探究过程,经历了这么几个阶 第一阶段:收集数据 画散点图(为了更加直观形象揭示变化规律 第二阶段:根据图象特征-一一选择适当函数类型,并求得函数类型 第三阶段:函数模型在实际问题中的应用
【师】从这这个问题可以看出,如果有时候时间控制不当,货船在卸货的过程中,就 会出现货还没有卸完,不得已要暂时驶离港口,进入深水区,等水位上帐后在驶回来。这 样对老板来说就会造成才力、物力上的巨大浪费?这显然不是老板愿意看到的。那改怎么 来做呢? (学生讨论) 【生】可以加快卸货速度,也就是加快安全深度下降速度。 【师】看下面这个问题: 问题探究 4:若船的吃水深度为 4 米,安全间隙为 1。5 米,该船在 2:00 开始卸货, 货物卸空后吃水深度为 2 米,为了保证进入码头后一次性卸空货物,又能安全驶离码头, 那么每小时吃水深度至少要以多少速度减少? (学生课后探究) 3.课时小结,认识深化 (师生一起归纳) 3-1 回顾我们整个探究过程,经历了这么几个阶段 第一阶段:收集数据-画散点图(为了更加直观形象揭示变化规律) 第二阶段:根据图象特征-选择适当函数类型,并求得函数类型 第三阶段:函数模型在实际问题中的应用

3-2在整个探究过程,我们用到数学常见的一些思想方法: (1)对实际问题处理过程是,首先是挖掘其中的数学本质,将实际问题转化为数学问 题:体现了数学中的转化思想: (2)在对一些数据处理的过程用到了估算的思想: (3)在用代数方法处理困难的一些题目的解决中,用到了数形结合的思想: (4)在方程的求解过程中,用到了算法中“二分法”思想。 【师】这节课我们利用数学中的三角函数处理了实际生活中货船进出港问题,这只是 三角函数在实际生产、生活中应用的“冰山一角”,希望大家在学习的过程做个有心人, 学会用数学的眼光去看待身边的一些自然和社会现象,同时并努力去尝试用学过的数学知 识处理一些实际问题。 4.作业布置,延时探究 4-1电视台的不同栏目播出的时间周期是不同的,有的每天播出,有的隔天播出,有 的一个星期播出一次。请查阅当地的电视节目预告,统计不同栏目的播出周期。 4-2请调查我们温州地区的每天的用电情况,制定一项“消蜂平谷”的电价方案。 43一个城市所在的经度和纬度是如何影响日出和日落的时间的?收集其他有关数据, 并提供理论证据支持你的结论
3-2 在整个探究过程,我们用到数学常见的一些思想方法: (1)对实际问题处理过程是,首先是挖掘其中的数学本质,将实际问题转化为数学问 题;体现了数学中的转化思想; (2)在对一些数据处理的过程用到了估算的思想; (3)在用代数方法处理困难的一些题目的解决中,用到了数形结合的思想; (4)在方程的求解过程中,用到了算法中“二分法”思想。 【师】这节课我们利用数学中的三角函数处理了实际生活中货船进出港问题,这只是 三角函数在实际生产、生活中应用的“冰山一角”,希望大家在学习的过程做个有心人, 学会用数学的眼光去看待身边的一些自然和社会现象,同时并努力去尝试用学过的数学知 识处理一些实际问题。 4.作业布置,延时探究 4-1 电视台的不同栏目播出的时间周期是不同的,有的每天播出,有的隔天播出,有 的一个星期播出一次。请查阅当地的电视节目预告,统计不同栏目的播出周期。 4-2 请调查我们温州地区的每天的用电情况,制定一项“消蜂平谷”的电价方案。 4-3 一个城市所在的经度和纬度是如何影响日出和日落的时间的?收集其他有关数据, 并提供理论证据支持你的结论